Skip to main content
SpringerLink
Log in

Dynamic characteristics of temperature-dependent viscoelastic FG nanobeams subjected to 2D-magnetic field under periodic loading

  • Published:
Applied Physics A Aims and scope Submit manuscript

Abstract

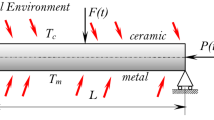
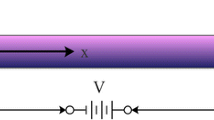
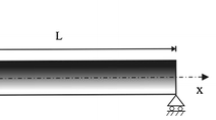
In this study, natural frequency and dynamic stability of functionally graded (FG) viscoelastic nanobeams based on the Euler–Bernoulli theory on the visco-Pasternak foundation are predicted. The material characteristics of FG nanobeam are temperature-dependent, and vary according to power-law model along thickness. The FG viscoelastic nanobeam is located on a two-dimensional magnetic field which considers the effects of transverse and longitudinal magnetic field. The uniform, linear, and sinusoidal temperature fields are applied on the FG viscoelastic nanobeam. The governing equations are derived through Hamilton’s principle and Eringen’s nonlocal theory. The equations are solved by a Navier-type method and the Bolotin method for simply supported conditions. The effect of three different temperature fields on natural frequency and dynamic stability region of the nanobeam is analyzed. The importance of various parameters such as nonlocal parameter, gradient indexes, magnitude of magnetic field, angle of magnetic field, temperature changes, and aspect ratio on both natural frequency and dynamic stability region of the FG viscoelastic nanobeam is investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. I. Bharti, N. Gupta, K.M. Gupta, Ijmmm 3, 221–224 (2013)

    Article  Google Scholar 

  2. E. Müller, Č. Drašar, J. Schilz, W.A. Kaysser, Mat. Sci. Eng A Struct. 362, 17–39 (2003)

    Article  Google Scholar 

  3. J. Woo, S.A. Meguid, L.S. Ong, J. Sound Vib. 289, 595–611 (2006)

    Article  ADS  Google Scholar 

  4. S. Abrate, Compos. Part B Eng. 39, 151–158 (2008)

    Article  Google Scholar 

  5. D.G. Zhang, Y.H. Zhou, Comput. Mater. Sci. 44, 716–720 (2008)

    Article  Google Scholar 

  6. M. Bourada, A. Kaci, M.S.A. Houari, A. Tounsi, Steel. Compos. Struct. 18, 409–423 (2015)

    Article  Google Scholar 

  7. A. Tounsi, M.S.A. Houari, A. Bessaim, Struct. Eng. Mech. 60, 547–565 (2016)

    Article  Google Scholar 

  8. A. Tounsi, M.S. A. Houari, S. Benyoucef, E.A. Adda Bedia, Aerosp. Sci. Technol. 24, 209–220 (2013)

    Article  Google Scholar 

  9. M.S.A. Houari, A. Tounsi, A. Bessaim, S.R. Mahmoud, Steel. Compos. Struct. 22, 257–276 (2016)

    Article  Google Scholar 

  10. A.C. Eringen, J. Appl. Phys. 54, 4703–4710 (1983)

    Article  ADS  Google Scholar 

  11. A. Ghorbanpour Arani, A. Fereidoon, R. Kolahchi, J. Intel. Mat. Syst. Str. 26, 1150–1163 (2015)

    Article  Google Scholar 

  12. D.S. Mashat, A.M. Zenkour, M. Sobhy, J. Mech. 32, 277–287 (2016)

    Article  Google Scholar 

  13. H.B. Li, X. Wang, Phys. E. 46, 198–205 (2012)

    Article  Google Scholar 

  14. A.A. Jandaghian, O. Rahmani, Smart. Mater. Struct. 25, 035023 (2016)

  15. A.A. Jandaghian, O. Rahmani, J. Mech. 32, 143–151 (2016)

    Article  Google Scholar 

  16. O. Rahmani, O. Pedram, Int. J. Eng. Sci. 77, 55–70 (2014)

    Article  Google Scholar 

  17. A. Besseghier, H. Heireche, A.A. Bousahla, A. Tounsi, A. Benzair. Adv. Nano Res. 3, 29–37 (2015)

    Article  Google Scholar 

  18. M. Akbarzadeh Khorshidi, M. Shariati, J. Braz. Soc. Mech. Sci. 38, 1–13 (2013)

    Google Scholar 

  19. M.A. Eltaher, S.A. Emam, F.F. Mahmoud, Appl. Math. Comput. 218, 7406–7420 (2012)

    MathSciNet  Google Scholar 

  20. M.A. Hamed, M.A. Eltaher, A.M. Sadoun, K.H. Almitani, Appl. Phys. A Mater. 122, 829 (2016)

  21. M. Simsek, H.H. Yurtcu, Compos. Struct. 97, 378–386 (2013)

    Article  Google Scholar 

  22. M. Simsek, Int. J. Eng. Sci. 105, 12–27 (2016)

    Article  MathSciNet  Google Scholar 

  23. F.L. Chaht, A. Kaci, M.S.A. Houari, A. Tounsi, O. Anwar Beg, S.R. Mahmoud, Steel. Compos. Struct. 18, 425–442 (2015)

    Article  Google Scholar 

  24. A.H. S. Hosseini, O. Rahmani, Appl. Phys. A Mater. 122, 1–11 (2016)

    Article  ADS  Google Scholar 

  25. M. Zamani Nejad, A. Hadi, Int. J. Eng. Sci. 105, 1–11 (2016)

    Article  Google Scholar 

  26. M. Zamani Nejad, A. Hadi, Int. J. Eng. Sci. 106, 1–9 (2016)

    Article  Google Scholar 

  27. F.L. Chaht, A. Kaci, M.S.A. Houari, A. Tounsi, O.A. Bég, Steel. Compos. Struct. 18, 425–442 (2015)

    Article  Google Scholar 

  28. M. Ahouel, M.S.A. Houari, E.A. Bedia, A. Tounsi, Steel. Compos. Struct. 20, 963–981 (2016)

    Article  Google Scholar 

  29. A. Zemri, M.S.A. Houari, A.A. Bousahla, A. Tounsi, Struct. Eng. Mech. 54, 693–710 (2015)

    Article  Google Scholar 

  30. K.S. Al-Basyouni, A. Tounsi, S.R. Mahmoud, Compos. Struct. 125, 621–630 (2015)

    Article  Google Scholar 

  31. I. Mechab, B. Mechab, S. Benaissa, B. Bachir Bouiadjra, J. Braz. Soc. Mech. Sci. 38, 1–19 (2016)

  32. R. Ansari, A. Norouzzadeh, Phys. E 84, 84–97 (2016)

    Article  Google Scholar 

  33. R. Ansari, A. Shahabodini, M. Faghih Shojaei, Phys. E 76, 70–81 (2016)

    Article  Google Scholar 

  34. H. Salehipour, H. Nahvi, A. R. Shahidi, Phys. E 66, 350–358 (2015)

    Article  Google Scholar 

  35. A. Fereidoon, H. Yaghoobi, A. Dehghanian, Int. J. Comput. Methods 11,1350099 (2014)

  36. H. Yaghoobi, A. Fereidoon, Comp. Part B Eng. 62, 54–64 (2014)

    Article  Google Scholar 

  37. A.H. S. Hosseini, O. Rahmani, J. Therm. Stress 39, 1–16 (2016)

    Article  Google Scholar 

  38. F. Ebrahimi, E. Salari, Comp. Part B Eng. 78, 272–290 (2015)

    Article  Google Scholar 

  39. F. Ebrahimi, M.R. Barati, Appl. Phys. A Mater. 122, 880 (2016)

  40. Sh.. Hosseini Hashemi, H. Mehrabani, A. Ahmadi-Savadkoohi, Compos. Struct. 133, 8–15 (2015)

    Article  Google Scholar 

  41. A. Fereidoon, E. Andalib, A. Mirafzal, Phys. E 81, 205–218 (2016)

    Article  Google Scholar 

  42. M. Hosseini, A. Jamalpoor, J. Therm. Stress 38, 1428–1456 (2015)

    Article  Google Scholar 

  43. F. Ebrahimi, M.R. Barati, Int. J. Eng. Sci. 107, 183–196 (2016)

    Article  Google Scholar 

  44. Y.S. Touloukian, Thermophysical Properties of High Temperature Solid Materials. (Macmillan, New York, 1967)

    Google Scholar 

  45. K. Kiani, J. Phys. Chem. Solids 75, 15–22 (2014)

    Article  ADS  Google Scholar 

  46. Y. Kiani, M.R. Eslami, Comp. Part B Eng. 45, 101–110 (2013)

    Article  Google Scholar 

  47. K.S. Na, J.H. Kim, Comp. Part B Eng. 35, 429–437 (2004)

    Article  Google Scholar 

  48. S.N. Patel, P.K. Datta, A.H. Sheikh, Thin Wall. Struct. 44, 321–333 (2006)

    Article  Google Scholar 

  49. T. Tauchert, Energy Principles in Structural Mechanics. (Mc Graw-Hill, 1974)

  50. A. Ghorbanpour Arani, Z. Khoddami Maraghi, Ain Shams Eng. J. 7, 361–369 (2016)

    Article  Google Scholar 

  51. V.V. Bolotin, The Dynamic Stability of Elastic Systems. (Holden-Day, San Francisco, 1964)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, Semnan University, Semnan, Iran

    A. Mirafzal & A. Fereidoon

Authors
  1. A. Mirafzal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Fereidoon
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Mirafzal.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mirafzal, A., Fereidoon, A. Dynamic characteristics of temperature-dependent viscoelastic FG nanobeams subjected to 2D-magnetic field under periodic loading. Appl. Phys. A 123, 247 (2017). https://doi.org/10.1007/s00339-017-0829-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00339-017-0829-1

Keywords

Search

Navigation