Skip to main content
SpringerLink
Log in

Equilateral Chains and Cyclic Central Configurations of the Planar Five-Body Problem

  • Published:
Journal of Nonlinear Science Aims and scope Submit manuscript

Abstract

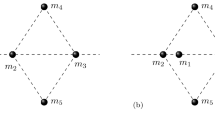
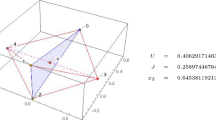
Central configurations and relative equilibria are an important facet of the study of the N-body problem, but become very difficult to rigorously analyze for \(N>3\). In this paper, we focus on a particular but interesting class of configurations of the five-body problem: the equilateral pentagonal configurations, which have a cycle of five equal edges. We prove a variety of results concerning central configurations with this property, including a computer-assisted proof of the finiteness of such configurations for any positive five masses with a range of rational-exponent homogeneous potentials (including the Newtonian case and the point-vortex model), some constraints on their shapes, and we determine some exact solutions for particular N-body potentials.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data Availability

All data generated or analyzed during this study are included in this published article.

References

  • Albouy, A.: Integral manifolds of the \(N\)-body problem. Invent. Math. 114, 463–488 (1993)

    MathSciNet  MATH  Google Scholar 

  • Albouy, A., Chenciner, A.: Le problème des n corps et les distances mutuelles. Invent. Math. 131(1), 151–184 (1997)

    MATH  Google Scholar 

  • Albouy, A., Kaloshin, V.: Finiteness of central configurations of five bodies in the plane. Ann. Math. 176(1), 535–588 (2012)

    MathSciNet  MATH  Google Scholar 

  • Alvarez-Ramírez, M., Gasull, A., Llibre, J.: On the equilateral pentagonal central configurations. Commun. Nonlinear Sci. Numer. Simul. 112, 106511 (2022)

    MathSciNet  MATH  Google Scholar 

  • Andoyer, H.: Sur l’équilibre relatif de n corps. Bull. Astron. 23, 50–59 (1906)

    Google Scholar 

  • Aref, H., Rott, N., Thomann, H.: Gröbli’s solution of the three-vortex problem. Annu. Rev. Fluid Mech. 24(1), 1–21 (1992)

    MATH  Google Scholar 

  • Bernshtein, D.N.: The number of roots of a system of equations. Func. Anal. Appl. 9(3), 1–4 (1975)

    MathSciNet  Google Scholar 

  • Brumberg, V.A.: Permanent configurations in the problem of four bodies and their stability. Sov. Astron. 1, 57–79 (1957)

    Google Scholar 

  • Cabral, H.E.: On the integral manifolds of the \(n\)-body problem. Invent. Math. 20(1), 59–72 (1973)

    MathSciNet  MATH  Google Scholar 

  • Celli, M.: Sur les mouvements homographiques de \(n\) corps associés à des masses de signe quelconque, le cas particulier où la somme des masses est nulle, et une application à la recherche de choréographies perverse. Ph.D. thesis, Université Paris 7, France (2005)

  • Chazy, J.: Sur certaines trajectoires du problème des n corp. Bull. Astronom. 35, 321–389 (1918)

    Google Scholar 

  • Chen, K.-C., Hsiao, J.-S.: Strictly convex central configurations of the planar five-body problem. Trans. AMS 370(3), 1907–1924 (2018)

    MathSciNet  MATH  Google Scholar 

  • Cornelio, J.L., Alvarez-Ramírez, M., Cors, J.M.: Central configurations in the five-body problem: rhombus plus one. Qual. Theory Dyn. Syst. 20(2), 1–13 (2021)

    MathSciNet  MATH  Google Scholar 

  • Decker, W., Greuel, G.-M., Pfister, G., Schönemann, H.: Singular 4-2-1—a computer algebra system for polynomial computations. http://www.singular.uni-kl.de (2021)

  • ElBialy, M.S.: Collision singularities in celestial mechanics. SIAM J. Math. Anal. 21(6), 1563–1593 (1990)

    MathSciNet  MATH  Google Scholar 

  • Euler, L.: De motu rectilineo trium corporum se mutuo attrahentium. Novi Commun. Acad. Sci. Imp. Petrop. 11, 144–151 (1767)

    Google Scholar 

  • Gidea, M., Llibre, J.: Symmetric planar central configurations of five bodies: Euler plus two. Cel. Mech. Dyn. Astron. 106(1), 89 (2010)

    MathSciNet  MATH  Google Scholar 

  • Hampton, M.: Stacked central configurations: new examples in the planar five-body problem. Nonlinearity 18(5), 2299–2304 (2005)

    MathSciNet  MATH  Google Scholar 

  • Hampton, M.: Finiteness of kite relative equilibria in the Five-Vortex and Five-Body problems. Qual. Theory Dyn. Syst. 8(2), 349–356 (2010)

    MathSciNet  MATH  Google Scholar 

  • Hampton, M., Jensen, A.N.: Finiteness of spatial central configurations in the five-body problem. Cel. Mech. Dyn. Astron. 109(4), 321–332 (2011)

    MathSciNet  MATH  Google Scholar 

  • Hampton, M., Jensen, A.N.: Finiteness of relative equilibria in the planar generalized \(n\)-body problem with fixed subconfigurations. J. Geom. Mech. 7, 35–42 (2015)

    MathSciNet  MATH  Google Scholar 

  • Hampton, M., Moeckel, R.: Finiteness of relative equilibria of the four-body problem. Invent. Math. 163(2), 289–312 (2005)

    MathSciNet  MATH  Google Scholar 

  • Hampton, M., Moeckel, R.: Finiteness of stationary configurations of the four-vortex problem. Trans. AMS 361(3), 1317–1332 (2009)

    MathSciNet  MATH  Google Scholar 

  • Hampton, M., Roberts, G.E., Santoprete, M.: Relative equilibria in the four-body problem with two pairs of equal vorticities. J. Nonlinear Sci. 24, 39–92 (2014)

    MathSciNet  MATH  Google Scholar 

  • Helmholtz, H.: Uber integrale der hydrodynamischen gleichungen, welche den wirbelbewegungen entsprechen. Crelle’s J. Math. 55 (1858), 25–55, English translation by P. G. Tait, P.G., On the integrals of the hydrodynamical equations which express vortex-motion. Philos. Mag. 485–451 (1867)

  • Jensen, A.N.: Gfan, a software system for Gröbner fans and tropical varieties (2011). http://home.imf.au.dk/jensen/software/gfan/gfan.html

  • Khovanskii, A.G.: Newton polyhedra and the genus of complete intersections. Funct. Anal. Appl. 12(1), 38–46 (1978)

    MathSciNet  Google Scholar 

  • Kirchhoff, G.: Vorlesungen über mathematische physik. B.G. Teubner (1883)

  • Kulevich, J.L., Roberts, G.E., Smith, C.J.: Finiteness in the planar restricted four-body problem. Qual. Theory Dyn. Syst. 8(2), 357–370 (2009)

    MathSciNet  MATH  Google Scholar 

  • Kushnirenko, A.G.: Newton polytopes and the Bezout theorem. Funct. Anal. Appl. 10(3), 233–235 (1976)

    MATH  Google Scholar 

  • Lagrange, J.L.: Essai sur le problème des trois corps, Œuvres, vol. 6. Gauthier-Villars, Paris (1772)

  • Laura, E.: Sulle equazioni differenziali canoniche del moto di un sistema di vortici elementari rettilinei e paralleli in un fluido incomprensibile indefinito. Atti della Reale Accad. Torino 40, 296–312 (1905)

    MATH  Google Scholar 

  • Leandro, E.S.G.: Structure and stability of the rhombus family of relative equilibria under general homogeneous forces. J. Dyn. Differ. Equ. 31(2), 933–958 (2019)

    MathSciNet  MATH  Google Scholar 

  • Lee, T.L., Santoprete, M.: Central configurations of the five-body problem with equal masses. Cel. Mech. Dyn. Astron. 104, 369–381 (2009)

    MathSciNet  MATH  Google Scholar 

  • Long, Y., Sun, S.: Four-body central configurations with some equal masses. Arch. Ration. Mech. Anal. 162(1), 25–44 (2002)

    MathSciNet  MATH  Google Scholar 

  • Maclagan, D., Sturmfels, B.: Introduction to Tropical Geometry. AMS, Providence (2015)

    MATH  Google Scholar 

  • MacMillan, W.D., Bartky, W.: Permanent configurations in the problem of four bodies. Trans. Am. Math. Soc. 34, 838–875 (1932)

    MathSciNet  MATH  Google Scholar 

  • Moczurad, M., Zgliczyński, P.: Central configurations in planar n-body problem with equal masses for \(n=5,6,7\). Cel. Mech. Dyn. Astron. 131, 1–28 (2019)

    MathSciNet  MATH  Google Scholar 

  • Moeckel, R.: Orbits of the three-body problem which pass infinitely close to triple collision. Am. J. Math. 103(6), 1323–1341 (1981)

    MathSciNet  MATH  Google Scholar 

  • Moeckel, R.: Chaotic dynamics near triple collision. Arch. Ration. Mech. Anal. 107(1), 37–69 (1989)

    MathSciNet  MATH  Google Scholar 

  • Moeckel, R.: On central configurations. Math. Z. 205(1), 499–517 (1990)

    MathSciNet  MATH  Google Scholar 

  • Moeckel, R.: Relative equilibria with clusters of small masses. J. Dyn. Differ. Equ. 9, 507–533 (1997)

    MathSciNet  MATH  Google Scholar 

  • Moeckel, R.: A proof of Saari’s conjecture for the three-body problem in \(r^d\). Discrete Contin. Dyn. Syst. Ser. S 1(4), 631–646 (2008)

    MathSciNet  MATH  Google Scholar 

  • Moeckel, R.: Central Configurations, Periodic Orbits, and Hamiltonian Systems. Springer, New York (2015)

    Google Scholar 

  • Moulton, F.R.: The straight line solutions of the problem of N bodies. Ann. Math. 12(1), 1–17 (1910)

    MathSciNet  MATH  Google Scholar 

  • Oliveira, A., Vidal, C.: Stability of the rhombus vortex problem with a central vortex. J. Dyn. Differ. Equ. 32(4), 2109–2123 (2020)

    MathSciNet  MATH  Google Scholar 

  • Perez-Chavela, E., Santoprete, M.: Convex four-body central configurations with some equal masses. Arch. Ration. Mech. Anal. 185(3), 481–494 (2007)

    MathSciNet  MATH  Google Scholar 

  • Rayl, A.S.: Stability of permanent configurations in the problem of four bodies. Ph.D. thesis, University of Chicago, Chicago (1939)

  • Roberts, G.E.: A continuum of relative equilibria in the five-body problem. Physica D 127(3–4), 141–145 (1999)

    MathSciNet  MATH  Google Scholar 

  • Saari, Donald G., Hulkower, Neal D.: On the manifolds of total collapse orbits and of completely parabolic orbits for the n-body problem. J. Differ. Equ. 41(1), 27–43 (1981)

    MathSciNet  MATH  Google Scholar 

  • Smale, S.: Mathematical problems for the next century. Math. Intell. 20, 7–15 (1998)

    MathSciNet  MATH  Google Scholar 

  • The Sage Developers: Sage mathematics software (Version 9.2) (2020). http://www.sagemath.org

  • Williams, W.L.: Permanent configurations in the problem of five bodies. Trans. AMS 44(3), 563–579 (1938)

    MathSciNet  MATH  Google Scholar 

  • Wintner, A.: The Analytical Foundations of Celestial Mechanics. Princeton University Press, Princeton (1941)

    MATH  Google Scholar 

  • Xia, Z.: Central configurations with many small masses. J. Differ. Equ. 91, 168–179 (1991)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Manuele Santoprete for the suggestion to study this class of configuration. Yiyang Deng was partially supported by the Mathematics and Statistics Team from Chongqing Technology and Business University (ZDPTTD201906).

Author information

Authors and Affiliations

  1. College of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing, 400067, China

    Yiyang Deng

  2. Department of Mathematics and Statistics, University of Minnesota Duluth, Duluth, MN, 55812, USA

    Marshall Hampton

Authors
  1. Yiyang Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marshall Hampton
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marshall Hampton.

Ethics declarations

Conflict of interest

The authors have no competing interests to declare.

Additional information

Communicated by Robert Buckingham.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Deng, Y., Hampton, M. Equilateral Chains and Cyclic Central Configurations of the Planar Five-Body Problem. J Nonlinear Sci 33, 4 (2023). https://doi.org/10.1007/s00332-022-09864-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00332-022-09864-z

Keywords

Mathematics Subject Classification

Search

Navigation