Dimension Reduction for the Landau-de Gennes Model on Curved Nematic Thin Films

Abstract

We use the method of $\Gamma$-convergence to study the behavior of the Landau-de Gennes model for a nematic liquid crystalline film attached to a general fixed surface in the limit of vanishing thickness. This paper generalizes the approach in Golovaty et al. (J Nonlinear Sci 25(6):1431–1451, 2015) where we considered a similar problem for a planar surface. Since the anchoring energy dominates when the thickness of the film is small, it is essential to understand its influence on the structure of the minimizers of the limiting energy. In particular, the anchoring energy dictates the class of admissible competitors and the structure of the limiting problem. We assume general weak anchoring conditions on the top and the bottom surfaces of the film and strong Dirichlet boundary conditions on the lateral boundary of the film when the surface is not closed. We establish a general convergence result to an energy defined on the surface that involves a somewhat surprising remnant of the normal component of the tensor gradient. Then we exhibit one effect of curvature through an analysis of the behavior of minimizers to the limiting problem when the substrate is a frustum.

Appendices

Appendix 1: Dimension Reduction for Parametric Surfaces

As an alternative to the approach to the dimension reduction carried out in the Section 3 here we formally outline a different argument leading to the same conclusion but using a parametric representation of the manifold $\mathcal M$. In addition to giving a different take on the limiting procedure, the parametric formulation was utilized in Sects. 5 and 6.

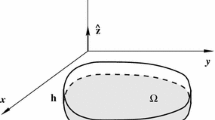
Suppose that the geometry of the problem is as shown in Fig. 1. We work in non-dimensional coordinates as specified in Sect. 2.4. The smoothness of $\mathcal {M}$ ensures that, for a given $x_0\in \mathcal {M}$, there is an open set $U\subset \mathbb R^2$ and a smooth function $\phi :U\rightarrow \mathcal {M}$ that (a) maps U homeomorphically onto an open neighborhood $V\subset \mathcal {M}$ of $x_0$ and (b) has a Jacobian matrix of rank 2 on U. Since the map $\phi ^{-1}:V\rightarrow U$ defines a local coordinate system on V, we can use the non-dimensional analog of (4) to introduce the coordinate system on $V\times \left[ -\varepsilon ,\varepsilon \right]$ via the smooth invertible map

$$\begin{aligned} X=x(u)+\varepsilon t\nu (x(u)), \end{aligned}$$

(74)

from $U\times [-1,1]$ to $\mathbb R^3$. Note that at a given point $x(u)\in \mathcal {M}$, we have

$$\begin{aligned} X_t=\varepsilon \nu , \end{aligned}$$

(75)

and

$$\begin{aligned} D_uX=D_ux\left( {I}+\varepsilon tA\right) , \end{aligned}$$

(76)

where

$$\begin{aligned} A=-\mathbb {I}^{-1}\mathbb {II}, \end{aligned}$$

(77)

is the matrix of the shape operator and $\mathbb {I}$ and $\mathbb {II}$ are the first and second fundamental forms for $\mathcal {M}$. The shape operator $\nabla _{\mathcal {M}}\nu$ is a symmetric operator acting on the tangent space of $\mathcal {M}$ that satisfies

$$\begin{aligned} \left( \nabla _{\mathcal {M}}\nu \right) \nu =0,\quad \left( \nabla _{\mathcal {M}}\nu \right) \mathbf{d}_1=\kappa _1\mathbf{d}_1,\quad \left( \nabla _{\mathcal {M}}\nu \right) \mathbf{d_2}=\kappa _2\mathbf{d}_2, \end{aligned}$$

(78)

with $\kappa _i$ and $\mathbf{d}_i,\ i=1,2$ being the principal curvatures and directions at x(u), respectively Walker (2015).

Given $X\in \Omega _\varepsilon$, let x be the closest point of $\mathcal {M}$ to X. The gradient of a smooth vector field $\mathbf{a}:V\times \left[ -\varepsilon ,\varepsilon \right] \rightarrow \mathbb R^3$ can be decomposed into orthogonal components along and perpendicular to $\nu (x)$ by writing

$$\begin{aligned} \nabla \mathbf{a}=\nabla \mathbf{a}(\nu \otimes \nu )+\nabla \mathbf{a}({I}-\nu \otimes \nu ). \end{aligned}$$

(79)

Indeed,

$$\begin{aligned}&\nabla \mathbf{a}(\nu \otimes \nu )\cdot \nabla \mathbf{a}({I}-\nu \otimes \nu )=(\nu \otimes \nu )\nabla \mathbf{a}\cdot ({I}-\nu \otimes \nu )\nabla \mathbf{a}\nonumber \\&\quad =\mathrm {tr}\,\left\{ \nabla \mathbf{a}({I}-\nu \otimes \nu )(\nu \otimes \nu )\nabla \mathbf{a}\right\} =0, \end{aligned}$$

(80)

so that

$$\begin{aligned} |\nabla \mathbf{a}|^2=\nabla \mathbf{a}\cdot \nabla \mathbf{a}={\left| \nabla \mathbf{a}(\nu \otimes \nu )\right| }^2+{\left| \nabla \mathbf{a}({I}-\nu \otimes \nu )\right| }^2. \end{aligned}$$

(81)

The change of variables (74) then transforms the components of the gradient of $\mathbf{a}$ as follows

$$\begin{aligned} \nabla \mathbf{a}(\nu \otimes \nu )= & {} D\mathbf{a}\,J^{-1}(\nu \otimes \nu )=\frac{1}{h}D{\mathbf a}\,({\mathbf e}_3\otimes \nu ), \end{aligned}$$

(82)

$$\begin{aligned} \nabla \mathbf{a}({I}-\nu \otimes \nu )= & {} D\mathbf{a}\,J^{-1}({I}-\nu \otimes \nu )=D\mathbf{a}\,({I}-{\mathbf e}_3\otimes {\mathbf e}_3)J^{-1}, \end{aligned}$$

(83)

where $J=\frac{\partial (X_1,X_2,X_3)}{\partial (u_1,u_2,t)}$ and $D{\mathbf a}$ is the gradient of ${\mathbf a}$ with respect to $(u_1,u_2,t)$. Introducing the projection matrix

$$\begin{aligned} P_X={I}-\nu (x)\otimes \nu (x), \end{aligned}$$

(84)

we conclude that

$$\begin{aligned} \nabla \mathbf{a}\left( {I}-P_X\right)= & {} \frac{1}{\varepsilon }{\mathbf a}_t\otimes \nu , \end{aligned}$$

(85)

$$\begin{aligned} \nabla \mathbf{a}\,P_X= & {} D_u{\mathbf a}\,{\left( {I}+\varepsilon tA\right) }^{-1}{\left( D_ux\right) }^{-1}=D_u{\mathbf a}\,\Psi (x,t;\varepsilon ), \end{aligned}$$

(86)

where ${\left( D_ux\right) }^{-1}$ is a left inverse of $D_ux$ and

$$\begin{aligned} \Psi (x,t;\varepsilon ):={\left( {I}+\varepsilon tA\right) }^{-1}{\left( D_ux\right) }^{-1}. \end{aligned}$$

(87)

Note that the matrix ${I}+\varepsilon tA$ is invertible when $\varepsilon$ is sufficiently small and setting $\varepsilon =0$ reduces the right hand side of (86) to

$$\begin{aligned} D_u{\mathbf a}{\left( D_ux\right) }^{-1}=\nabla _{\mathcal M}{\mathbf a}, \end{aligned}$$

(88)

where $\nabla _{\mathcal M}{\mathbf a}$ is the surface gradient of ${\mathbf a}$ defined earlier in (20).

In non-dimensional coordinates, we can rewrite the expression for the elastic energy (12) as follows

$$\begin{aligned} f_e(\nabla Q)= & {} \frac{1}{2}\sum _{i=1}^3\left\{ {|\nabla Q_iP_X+\nabla Q_i({I}-P_X)|}^2+M_2\left( \mathrm {tr}\,{(\nabla Q_iP_X)}+\mathrm {tr}\,{(\nabla Q_i({I}-P_X))}\right) ^2\right. \nonumber \\&\left. +M_3(\nabla Q_iP_X+\nabla Q_i({I}-P_X))\cdot (P_X\nabla Q_i^T+({I}-P_X)\nabla Q_i^T)\right\} \nonumber \\= & {} \frac{1}{2}\sum _{i=1}^3\left\{ {\left| D_u{Q_i}\,\Psi (x,t;\varepsilon )+\frac{1}{\varepsilon }Q_{i,t}\otimes \nu \right| }^2+M_2{\left( D_u{Q_i}\cdot \Psi (x,t;\varepsilon )^T+\frac{1}{\varepsilon }Q_{i,t}\cdot \nu \right) }^2\right. \nonumber \\&+\left. M_3\left( D_u{Q_i}\,\Psi (x,t;\varepsilon )+\frac{1}{\varepsilon }Q_{i,t}\otimes \nu \right) \cdot \left( \Psi (x,t;\varepsilon )^TD_u{Q_i}^T+\frac{1}{\varepsilon }\nu \otimes Q_{i,t}\right) \right\} \nonumber \\= & {} \frac{1}{2}\sum _{i=1}^3\left\{ {\left| D_u{Q_i}\,{\left( D_ux\right) }^{-1}+\frac{1}{\varepsilon }Q_{i,t}\otimes \nu \right| }^2+M_2{\left( D_u{Q_i}\cdot {\left( D_ux\right) }^{-T}+\frac{1}{\varepsilon }Q_{i,t}\cdot \nu \right) }^2\right. \nonumber \\&+\left. M_3\left( D_u{Q_i}\,{\left( D_ux\right) }^{-1}+\frac{1}{\varepsilon }Q_{i,t}\otimes \nu \right) \cdot \left( {\left( D_ux\right) }^{-T}D_u{Q_i}^T+\frac{1}{\varepsilon }\nu \otimes Q_{i,t}\right) \right\} +O(\varepsilon ),\nonumber \\ \end{aligned}$$

(89)

when $\varepsilon$ is small. The same arguments that led to the proof of Threorem 3.1 demonstrate that the limiting elastic energy density is given by (34), that is

$$\begin{aligned} f_{e}^0\left( \nabla _{\mathcal M}Q,\nu \right)= & {} \frac{1}{2}\min _{ G\in \mathcal A}\Bigg [\sum _{i=1}^3\bigg \{{\left| \nabla _{\mathcal M}Q_i+ G_i\otimes \nu \right| }^2+M_2{\left( \mathrm {div}_{\mathcal M}Q_i+ G_i\cdot \nu \right) }^2\nonumber \\&+M_3\left( \nabla _{\mathcal M}Q_i+ G_i\otimes \nu \right) \cdot \left( {\left( \nabla _{\mathcal M}Q_i\right) }^T+\nu \otimes G_i\right) \bigg \}\Bigg ], \end{aligned}$$

(90)

where $\nabla _{\mathcal M}Q_i=D_u{Q_i}\,{\left( D_ux\right) }^{-1}$ and $\mathrm {div}_{\mathcal M}Q_i=\mathrm {tr}\,\nabla _{\mathcal M}Q_i=D_u{Q_i}\cdot {\left( D_ux\right) }^{-T}$, respectively, for $i=1,\ldots ,3$.

Appendix 2: Outline of the Proof of Lemma 4.2

In order find the expression for $f_{e}^0\left( \nabla _{\mathcal M}Q,\nu \right)$ recall that in (34) we need to minimize

$$\begin{aligned} \phi [G]:= & {} \sum _{i=1}^3\left\{ \left( M_2\left( \mathrm {div}_{\mathcal M}Q_i\right) \nu +M_3{\left( \nabla _{\mathcal M}Q_i\right) }^T\nu \right) \right. \nonumber \\&\left. \cdot G_i+\frac{1}{2}{\left| G_i\right| }^2+\frac{1}{2}(M_2+M_3){( G_i\cdot \nu )}^2\right\} . \end{aligned}$$

(91)

among all $G\in \mathcal A$. To this end, set $\zeta =M_2+M_3$ and let the columns of the matrix $U\in M^{3\times 3}$ be given by

$$\begin{aligned} U_i=M_2\left( \mathrm {div}_{\mathcal M}Q_i\right) \nu +M_3{\left( \nabla _{\mathcal M}Q_i\right) }^T\nu , \end{aligned}$$

where $i=1,\ldots ,3$. The Eq. (91) can now be written as

$$\begin{aligned} \phi [G]=U\cdot G+\frac{1}{2}{\left| G\right| }^2+\frac{\zeta }{2}{|G\nu |}^2. \end{aligned}$$

(92)

Using the same procedure as in Lemma 4.1, we obtain that

$$\begin{aligned} \bar{G}= & {} -D(U)+\frac{\zeta }{\zeta +2}\left( \nu \otimes D(U)\nu +D(U)\nu \otimes \nu \right) \nonumber \\&-\frac{\zeta \left( \zeta U\nu \cdot \nu +(\zeta +2)\,\mathrm {tr}\,U\right) }{(\zeta +2)(2\zeta +3)}\nu \otimes \nu -\frac{\zeta U\nu \cdot \nu -(\zeta +1)\,\mathrm {tr}\,U}{2\zeta +3}I \end{aligned}$$

(93)

minimizes (92), where

$$\begin{aligned} D(U)=\frac{1}{2}\left( U+U^T\right) . \end{aligned}$$

Next, substituting $\bar{G}$ into (93) and following a lengthy sequence of trivial calculations, the minimum value of $\phi$ is given by

$$\begin{aligned} \phi [\bar{G}]= & {} -\frac{1}{2}{|D(U)|}^2+\frac{\zeta }{\zeta +2}{|D(U)\nu |}^2-\frac{\zeta ^2}{2(\zeta +2)(2\zeta +3)}{(U\nu \cdot \nu )}^2\nonumber \\&-\frac{\zeta }{2\zeta +3}(U\nu \cdot \nu )\,\mathrm {tr}\,(U)+\frac{\zeta +1}{2(2\zeta +3)}\,\mathrm {tr}\,^2(U). \end{aligned}$$

(94)

The conclusion of Lemma 4.2 then follows from (94) with the help of the identities

$$\begin{aligned} D(U)\nu= & {} \frac{M_2}{2}\left( \mathrm {div}_{\mathcal M}Q+\left( \mathrm {div}_{\mathcal M}Q\cdot \nu \right) \nu \right) +\frac{M_3}{2}\sum _{i=1}^3\nu _i\nabla _{\mathcal M}Q_i^T\nu ,\\ U\nu \cdot \nu= & {} M_2\,\nu \cdot \mathrm {div}_{\mathcal M}Q, \\ \mathrm {tr}\,(U)= & {} (M_2+M_3)\,\nu \cdot \mathrm {div}_{\mathcal M}Q. \end{aligned}$$