New Approximations and Tests of Linear Fluctuation-Response for Chaotic Nonlinear Forced-Dissipative Dynamical Systems

Abstract

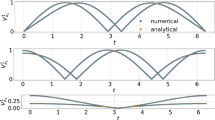
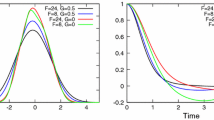
We develop and test two novel computational approaches for predicting the mean linear response of a chaotic dynamical system to small change in external forcing via the fluctuation–dissipation theorem. Unlike the earlier work in developing fluctuation–dissipation theorem-type computational strategies for chaotic nonlinear systems with forcing and dissipation, the new methods are based on the theory of Sinai–Ruelle–Bowen probability measures, which commonly describe the equilibrium state of such dynamical systems. The new methods take into account the fact that the dynamics of chaotic nonlinear forced-dissipative systems often reside on chaotic fractal attractors, where the classical quasi-Gaussian formula of the fluctuation–dissipation theorem often fails to produce satisfactory response prediction, especially in dynamical regimes with weak and moderate degrees of chaos. A simple new low-dimensional chaotic nonlinear forced-dissipative model is used to study the response of both linear and nonlinear functions to small external forcing in a range of dynamical regimes with an adjustable degree of chaos. We demonstrate that the two new methods are remarkably superior to the classical fluctuation–dissipation formula with quasi-Gaussian approximation in weakly and moderately chaotic dynamical regimes, for both linear and nonlinear response functions. One straightforward algorithm gives excellent results for short-time response while the other algorithm, based on systematic rational approximation, improves the intermediate and long time response predictions.