Optimal control of bacterial growth for the maximization of metabolite production

Abstract

Microorganisms have evolved complex strategies for controlling the distribution of available resources over cellular functions. Biotechnology aims at interfering with these strategies, so as to optimize the production of metabolites and other compounds of interest, by (re)engineering the underlying regulatory networks of the cell. The resulting reallocation of resources can be described by simple so-called self-replicator models and the maximization of the synthesis of a product of interest formulated as a dynamic optimal control problem. Motivated by recent experimental work, we are specifically interested in the maximization of metabolite production in cases where growth can be switched off through an external control signal. We study various optimal control problems for the corresponding self-replicator models by means of a combination of analytical and computational techniques. We show that the optimal solutions for biomass maximization and product maximization are very similar in the case of unlimited nutrient supply, but diverge when nutrients are limited. Moreover, external growth control overrides natural feedback growth control and leads to an optimal scheme consisting of a first phase of growth maximization followed by a second phase of product maximization. This two-phase scheme agrees with strategies that have been proposed in metabolic engineering. More generally, our work shows the potential of optimal control theory for better understanding and improving biotechnological production processes.

1 Introduction

The fitness of microorganisms is defined by their capacity to propagate in environments hosting a variety of competitors for available resources. The situation faced by these single-cell organisms can be seen as an optimization problem: the allocation of resources to different cellular functions so as to maximize fitness. In many situations, microbial fitness amounts to maximizing the growth rate of the population, allowing the cells to outgrow competitors. However, depending on the structure of the environment and the properties of metabolic pathways, other fitness criteria may apply as well (Schuetz et al. 2007; Schuster et al. 2008). While experimental conditions can be kept constant in the laboratory, in most natural environments microorganisms are exposed to changing conditions (Savageau 1983; van Elsas et al. 2011). This requires microbial cells to continually adapt their functioning, and the allocation of resources to maximize fitness can be viewed as a dynamical optimization problem (see Banga 2008; Lenhart and Workman 2007 for general introductions to dynamical optimization problems in biology).

Self-replicator models (Hinshelwood 1952; Koch 1988) have been shown to provide a fruitful description of microbial growth. Despite their simplicity, they are remarkably expressive and are capable of accounting for observed correlations between variables in microbial physiology (Molenaar et al. 2009). In recent years, self-replicator models have been used to formulate resource allocation in microorganisms as an optimal control problem (Giordano et al. 2016; Pavlov and Ehrenberg 2013; Scott et al. 2014; van den Berg et al. 1998; Yegorov et al. 2017b, 2018). For the purpose of optimal control, self-replicator models are of great interest, since they reduce the mathematical and computational complexity of the problem. The optimal solutions thus obtained may give new insights into the functioning of microorganisms, by comparing them with control strategies that microorganisms have evolved to distribute available resources over cellular functions, involving complex networks of regulatory interactions on the molecular level (Chubukov et al. 2014; Schaechter et al. 2006).

In addition to gaining a better understanding of naturally-evolved resource allocation, optimal control theory is also beneficial in biotechnology, where the objective is not to optimize microbial growth, but to exploit the synthetic capacities of microorganisms for maximizing the production of compounds of interest (Stephanopoulos et al. 1998). Control theory has contributed a rich variety of mathematical and computational tools for achieving this, notably through on-line estimation, adaptive control and optimization of process conditions (Banga et al. 2005; Bastin and Dochain 1990; Venkateswarlu 2005). The emergence of systems biology and synthetic biology has provided new tools for the implementation of control strategies, by increasing our understanding of the functioning of regulatory networks on the molecular level and facilitating their (re)engineering (Chubukov et al. 2014; Khalil and Collins 2010).

An example of a synthetic biology application in biotechnology is the development of an E. coli strain that allows growth to be switched on and off externally by adjusting the availability of RNA polymerase, a major component of the gene expression machinery. It was shown that by arresting the expression of the $\beta \beta '$ subunits of RNA polymerase, resources are shuttled away from protein synthesis (growth) to the production of a metabolite of interest (glycerol) (Izard et al. 2015). Other examples of synthetic growth-rate control, with possible applications in biotechnology, have been published in the literature recently (Ceroni et al. 2016; Lo et al. 2016; Milias-Argeitis et al. 2016).

Self-replicator models provide a useful conceptual framework for expressing the dynamical reallocation of resources in microorganisms as an optimal control problem (de Jong et al. 2017b). In this study, we aim at exploiting this potential by reformulating the redirection of resources from growth to metabolite production via the growth switch as a dynamical optimal control problem. We thus hope to answer the question which strategy for the dynamical regulation of RNA polymerase expression maximizes metabolite production and how this strategy compares with the approach followed in the original publication (Izard et al. 2015). Whereas previous studies using self-replicator models focused on natural growth control (Giordano et al. 2016; Pavlov and Ehrenberg 2013; Scott et al. 2014; van den Berg et al. 1998; Yegorov et al. 2018), we here explore their use for biotechnological applications. The emphasis on resource allocation using a coarse-grained, whole-cell model of microbial growth distinguishes our work from previous application of (optimal) control in biotechnology (Banga et al. 2005; Bastin and Dochain 1990; Venkateswarlu 2005).

We first formulate a model of a self-replicator extended with a pathway for the production of a metabolite of interest as well as external control of the synthesis of components of the gene expression machinery. We consider the scenarios of limited and unlimited nutrient availability, corresponding roughly to batch and fed-batch cultivation modes, respectively. Given the control input for these models, modulation of the synthesis rate of components of the gene expression machinery, we then formulate two dynamical optimal control problems, the first one involving maximization of metabolite production, and the second one involving maximization of biomass production. We solve the optimal control problems by analytical and numerical means, and notably find that the optimal solutions for product maximization and biomass maximization are very similar in the case of the model with unlimited nutrient supply, but become essentially different when the available nutrients are limited.

The solutions thus obtained provide a gold standard in the sense that they represent the optimum that can be theoretically achieved, under the assumption that external control of the gene expression machinery completely overrides natural feedback growth control in bacteria. Since the two are expected to interfere in biotechnological applications, we adapt the model, in a final step, to account for natural feedback growth control. We show that the gold standard can be closely approximated when assuming a simple two-step control scheme: a first phase with maximal induction of the gene expression machinery (and low production), followed by a second phase with no induction of the gene expression machinery (and high production). The practical relevance of this control scheme is assessed by comparing it with established strategies of dynamical process control (Venayak et al. 2015).

2 Self-replicator models of the control of metabolite production

Figure 1a is a schematic representation of the self-replicator model of bacterial growth proposed by Giordano et al. (2016). Incoming nutrients S are transformed into precursor metabolites P, which are then consumed by several cellular functions, here limited to gene expression and metabolism. More precisely, the precursor metabolites are utilized for ribosomes and other components of the gene expression machinery (R) as well as the enzymes making up the metabolic machinery (M). M enables the conversion of external substrates into precursors, while R is responsible for the production of M and R itself. The (auto-)catalytic activity of M and R thus allows the cell to replicate its protein contents, the major constituent of biomass. The allocation of resources over the two different cellular functions considered here, metabolism and gene expression, is captured by the time-varying function $\, \alpha = \alpha (t) \in [0, 1], \,$ which indicates the proportional utilization of precursors for the synthesis of R and M.

Fig. 1

Self-replicator models of bacterial growth and metabolite production. a Original self-replicator model from Giordano et al. (2016), describing the synthesis of precursor metabolite P from external substrate S, and the utilization of P for the synthesis of gene expression machinery R and metabolic machinery M, at proportions $\alpha$ and $1 - \alpha$, respectively. $V_M$ and $V_R$ denote the rates of precursor and protein synthesis, respectively. M catalyzes precursor synthesis and R protein synthesis. b Extended self-replicator model in which a heterologous pathway allows the cell to produce metabolite X from precursor P, at a rate $V_X$. Moreover, following Izard et al. (2015), the synthesis of gene expression machinery R can be modulated by an external signal I

In order to reengineer natural resource allocation strategies for biotechnological applications, we consider extended self-replicators including a heterologous (non-natural) metabolic pathway for the production of a metabolite of interest X (Fig. 1b). X may be a drug precursor or a biofuel. Moreover, we extend the self-replicator with the growth switch as described by Izard et al. (2015), which allows the synthesis of (components of) the gene expression machinery, in particular RNA polymerase, to be shut off by means an external control signal I. The original growth switch uses a chemical signal, but alternatively a light signal could be employed (Milias-Argeitis et al. 2016; Olson and Tabor 2014). While a chemical inducer can be simply added to the growth medium of a bacterial population, it cannot be easily removed, contrary to a light signal which can be switched on and off. The basic idea underlying the growth switch is that upon arresting synthesis of (components of) the gene expression machinery, precursors P are decreasingly utilized for protein synthesis which causes growth to slow down. As a consequence, P becomes available for the production of X and, under the assumption that the enzymes necessary for producing P and X are abundant and stable, so that metabolism remains active, resources are reallocated from growth to metabolite production.

The extended self-replicator of Fig. 1b is described in terms of the time-varying variables S, P, M, R, X representing the masses of S, P, M, R, X $[\mathrm {g}]$, respectively. Their dynamics are given by the following system of ordinary differential equations:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dS(t)}{dt} \, = \, V_S(t) \, - \, V_M(t), \\&\frac{dP(t)}{dt} \, = \, V_M(t) \, - \, V_R(t) \, - \, V_X(t), \\&\frac{dM(t)}{dt} \, = \, (1 - u(t)) \, V_R(t), \\&\frac{dR(t)}{dt} \, = \, u(t) \, V_R(t), \\&\frac{dX(t)}{dt} \, = \, V_X(t), \\&t \in [0, T]. \end{aligned}\right. \end{aligned}$$

(1)

Here t $[\mathrm {h}]$ is the time variable, $\, T \in (0, +\infty )$ $\, [\mathrm {h}] \,$ is a finite time horizon, and the quantities

$$\begin{aligned} V_S= & {} V_S(t) \,\, \left[ \mathrm {g} \ \mathrm {h}^{-1} \right] , \quad V_M = V_M(t) \,\, \left[ \mathrm {g} \ \mathrm {h}^{-1} \right] , \\ V_R= & {} V_R(t) \,\, \left[ \mathrm {g} \ \mathrm {h}^{-1} \right] , \quad V_X = V_X(t) \,\, \left[ \mathrm {g} \ \mathrm {h}^{-1} \right] \end{aligned}$$

represent the rates of supplying the external substrate, producing the precursors by metabolism, utilizing the precursors for protein synthesis, and producing the metabolite of interest, respectively. The precursor mass used for protein synthesis is allocated between the gene expression and metabolic machineries. The dimensionless resource allocation (control) function $\, u = u(t) \in [0, 1] \,$ specifies the proportion utilized for gene expression, while $1 - u(t)$ is the proportion allocated to metabolism.

We set

$$\begin{aligned} u(t) \, = \, I(t) \, \alpha (t), \end{aligned}$$

(2)

that is, the input u aggregates the external control I and the control $\alpha$ exerted by the natural resource allocation systems of the cells. By (2), the natural and synthetic controls are supposed to act independently. Assume that $\, \alpha = \alpha (t) \in [\alpha _{\min }, \alpha _{\max }] \,$ and $\, I = I(t) \in [I_{\min }, I_{\max }], \,$ where the constant parameters $I_{\min }, I_{\max }, \alpha _{\min }, \alpha _{\max }$ satisfy the inequalities

$$\begin{aligned} 0\leqslant & {} I_{\min }< 1, \quad I_{\min }< I_{\max } \leqslant 1, \nonumber \\ 0\leqslant & {} \alpha _{\min }< 1, \quad \alpha _{\min } < \alpha _{\max } \leqslant 1. \end{aligned}$$

(3)

Then the lower and upper bounds for u are given by

$$\begin{aligned} u_{\min } \, {\mathop {=}\limits ^{\mathrm {def}}} \, I_{\min } \, \alpha _{\min } \, \in \, [0, 1), \quad u_{\max } \, {\mathop {=}\limits ^{\mathrm {def}}} \, I_{\max } \, \alpha _{\max } \, \in \, (u_{\min }, 1]. \end{aligned}$$

(4)

The model presented above makes a number of simplifications. First, protein degradation is ignored, i.e., we suppose that the macromolecules are stable and that their degradation rates are negligible with respect to the rates of the reactions described above. This is a reasonable assumption for normal physiological conditions, in which most bacterial proteins have a half-life $> 10$ h (Larrabee et al. 1980; Mosteller et al. 1980). At high temperatures, however, the influence of degradation may become significant (Farewell and Neidhardt 1998; Johnson and Lewin 1946), as was also shown by Yegorov et al. (2018) for a variant of the self-replicator model of Fig. 1a. Second, only two classes of macromolecules, corresponding to the metabolic and gene expression machineries, are taken into account. We thus neglect the use of precursors for the synthesis of proteins involved in, for example, cell maintenance (Scott et al. 2010), as well as in sensing and regulation (Kalisky et al. 2007; Poelwijk et al. 2011). Third, we describe the growing cell population on the level of the aggregated masses of its components P, M, R, X. The use of such nonsegregated models, as opposed to segregated models taking individual cells into account (Surovstev et al. 2007), relies on the implicit assumption that individual cells in the population are sufficiently similar to each other (de Jong et al. 2017a).

The above model can be further developed by making a number of additional assumptions and transformations.

First, in line with Giordano et al. (2016), we assume that the cytoplasmic density of the cells in the population is constant, and $\, \beta > 0$ $\left[ \mathrm {L} \ \mathrm {g}^{-1} \right] \,$ denotes the inverse density. Second, the growing structural volume of the bacterial population is defined as

$$\begin{aligned} {\mathcal {V}} \, = \, {\mathcal {V}}(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \beta \cdot (M(t) + R(t)) \,\,\, [\mathrm {L}]. \end{aligned}$$

(5)

In other words, the volume is proportional to the macromolecules constituting the metabolic and gene expression machineries, consistent with the fact that macromolecules make up most of the biomass of microbial cells (Bremer and Dennis 2013). Third, the relative increase in the volume determines the growth rate

$$\begin{aligned} \mu \, = \, \mu (t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \frac{1}{{\mathcal {V}}(t)} \, \frac{d {\mathcal {V}}(t)}{dt}. \end{aligned}$$

(6)

Fourth, we introduce variables that express the mass quantities $P, R, M, V_M, V_R$ per unit population volume:

$$\begin{aligned} \begin{aligned} p \,&= \, p(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{P(t)}{{\mathcal {V}}(t)} \,\,\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \right] , \\ r \,&= \, r(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{R(t)}{{\mathcal {V}}(t)} \,\,\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \right] , \\ m \,&= \, m(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{M(t)}{{\mathcal {V}}(t)} \,\,\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \right] , \\ v_M \,&= \, v_M(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{V_M(t)}{{\mathcal {V}}(t)} \,\,\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \ \mathrm {h}^{-1} \right] , \\ v_R \,&= \, v_R(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{V_R(t)}{{\mathcal {V}}(t)} \,\,\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \ \mathrm {h}^{-1} \right] . \end{aligned} \end{aligned}$$

(7)

The variables p, r, m thus represent the concentrations of precursors, gene expression machinery, and metabolic machinery, respectively, in the growing bacterial population, and $v_M, v_R$ the rate of production of precursors and proteins, respectively. From the relation (5), one can see that the sum $p(t) + r(t)$ is constant and equal to $1 / \beta$, so that

$$\begin{aligned} m(t) \, = \, \frac{1}{\beta } \, - \, r(t). \end{aligned}$$

(8)

Fifth, consider the quantities

$$\begin{aligned} x \,= & {} \, x(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{X(t)}{{\mathcal {V}}(t)} \,\,\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \right] , \nonumber \\ v_X \,= & {} \, v_X(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{V_X(t)}{{\mathcal {V}}(t)} \,\,\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \ \mathrm {h}^{-1} \right] . \end{aligned}$$

(9)

They are needed mainly for the mathematical investigation below and do not have a clear biological interpretation (because the metabolite of interest is assumed to be excreted from the cells).

Sixth, we define the nutrient concentration

$$\begin{aligned} s \, = \, s(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \frac{S(t)}{{\mathcal {V}}_{\mathrm {ext}}} \,\,\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \right] \end{aligned}$$

(10)

with respect to a constant external volume $\, {\mathcal {V}}_{\mathrm {ext}} > 0$$\, [\mathrm {L}] \,$ and set

$$\begin{aligned} v_S \, = \, v_S(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \frac{V_S(t)}{{\mathcal {V}}_{\mathrm {ext}}} \,\,\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \ \mathrm {h}^{-1} \right] . \end{aligned}$$

(11)

With the above definitions, the system (1) can be rewritten in the form

$$\begin{aligned} \left\{ \begin{aligned}&\frac{ds(t)}{dt} \, = \, v_S(t) \, - \, v_M(t) \, \frac{{\mathcal {V}}(t)}{{\mathcal {V}}_{\mathrm {ext}}}, \\&\frac{dp(t)}{dt} \, = \, v_M(t) \, - \, v_R(t) \, - \, v_X(t) \, - \, \mu (t) \, p(t), \\&\frac{dr(t)}{dt} \, = \, u(t) \, v_R(t) \, - \, \mu (t) \, r(t), \\&\frac{dx(t)}{dt} \, = \, v_X(t) \, - \, \mu (t) \, x(t), \\&\frac{d {\mathcal {V}}(t)}{dt} \, = \, \mu (t) \, {\mathcal {V}}(t), \\&m(t) \, = \, \frac{1}{\beta } \, - \, r(t), \quad X(t) \, = \, x(t) \, {\mathcal {V}}(t), \\&t \in [0, T]. \end{aligned}\right. \end{aligned}$$

(12)

Following Giordano et al. (2016), we suppose that

$$\begin{aligned}&v_M(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, m(t) \, k_M \, \dfrac{s(t)}{K_M + s(t)}, \nonumber \\&v_R(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, r(t) \, k_R \, \dfrac{p(t)}{K_R + p(t)}. \end{aligned}$$

(13)

Here $\, k_M > 0$$\, \left[ \mathrm {h}^{-1} \right] \,$ and $\, K_M > 0$$\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \right] \,$ are respectively the rate and half-saturation constants for the metabolic macroreaction, while $\, k_R > 0$$\, \left[ \mathrm {h}^{-1} \right] \,$ and $\, K_R > 0$$\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \right] \,$ are those for the protein synthesis reaction. By using the relations (1), (5)–(7) and (13), one can reformulate the growth rate as

$$\begin{aligned} \mu (t) \, = \, \beta \, v_R(t) \, = \, \beta \, r(t) \, k_R \, \frac{p(t)}{K_R + p(t)}. \end{aligned}$$

(14)

We also set

$$\begin{aligned} v_X(t) \, {\mathop {=}\limits ^{\mathrm {def}}} \, m(t) \, k_X \, \frac{p(t)}{K_X + p(t)}, \end{aligned}$$

(15)

where $\, k_X > 0$$\, \left[ \mathrm {h}^{-1} \right] \,$ and $\, K_X > 0$$\, \left[ \mathrm {g} \ \mathrm {L}^{-1} \right] \,$ are the rate and half-saturation constants for the reaction producing the metabolite of interest. The expressions for the reaction rates $v_M, v_R, v_X$ and the growth rate $\mu$ complete the system (12).

For the analysis below, it is convenient to introduce the following new variables and parameters (most of which are dimensionless):

$$\begin{aligned} \begin{aligned}&{\hat{t}} \, {\mathop {=}\limits ^{\mathrm {def}}} \, k_R \, t, \quad {\hat{T}} \, {\mathop {=}\limits ^{\mathrm {def}}} \, k_R \, T, \\&{\hat{p}} \left( {\hat{t}} \right) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \beta \, p(t), \quad {\hat{r}} \left( {\hat{t}} \right) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \beta \, r(t),\\&{\hat{m}} \left( {\hat{t}} \right) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \beta \, m(t) \, = \, 1 \, - \, {\hat{r}} \left( {\hat{t}} \right) , \\&{\hat{X}} \left( {\hat{t}} \right) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \beta \, X(t), \quad {\hat{x}} \left( {\hat{t}} \right) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \beta \, x(t), \\&{\hat{s}} \left( {\hat{t}} \right) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \beta \, s(t), \quad {\hat{v}}_S \left( {\hat{t}} \right) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{\beta }{k_R} \, v_S(t), \\&K \, {\mathop {=}\limits ^{\mathrm {def}}}\, \beta \, K_R, \quad K_1 \, {\mathop {=}\limits ^{\mathrm {def}}} \, \beta \, K_X, \quad K_2 \, {\mathop {=}\limits ^{\mathrm {def}}} \, \beta \, K_M,\\&k_1 \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{k_X}{k_R}, \quad k_2 \, {\mathop {=}\limits ^{\mathrm {def}}} \, \dfrac{k_M}{k_R}. \end{aligned} \end{aligned}$$

(16)

We also consider the structural volume ${\mathcal {V}}$ and control strategy u as functions of the new time variable ${\hat{t}}$: $\, {\mathcal {V}} = {\mathcal {V}} \left( {\hat{t}} \right)$, $\, u = u \left( {\hat{t}} \right)$. Moreover, the rescaled growth rate becomes

$$\begin{aligned} {\hat{\mu }} \left( {\hat{t}} \right) \, = \, \frac{\mu (t)}{k_R} \, = \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, {\hat{r}} \left( {\hat{t}} \right) }{K \, + \, {\hat{p}} \left( {\hat{t}} \right) }. \end{aligned}$$

(17)

With these definitions, (12) transforms into the following nonlinear system:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{d {\hat{s}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, {\hat{v}}_S \left( {\hat{t}} \right) \,\, - \,\, k_2 \, \frac{{\hat{s}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_2 + {\hat{s}} \left( {\hat{t}} \right) } \, \frac{{\mathcal {V}} \left( {\hat{t}} \right) }{{\mathcal {V}}_{\mathrm {ext}}}, \\&\frac{d {\hat{p}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, k_2 \, \frac{{\hat{s}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_2 + {\hat{s}} \left( {\hat{t}} \right) } \,\, - \,\, \left( 1 + {\hat{p}} \left( {\hat{t}} \right) \right) \, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \,\, \\&\qquad \qquad \quad -\, k_1 \, \frac{{\hat{p}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) }, \\&\frac{d {\hat{r}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, \left( u \left( {\hat{t}} \right) - {\hat{r}} \left( {\hat{t}} \right) \right) \, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) }, \\&\frac{d {\hat{x}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, k_1 \, \frac{{\hat{p}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) } \,\, - \,\, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, {\hat{x}} \left( {\hat{t}} \right) , \\&\frac{d {\mathcal {V}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, {\mathcal {V}} \left( {\hat{t}} \right) , \\&{\hat{m}} \left( {\hat{t}} \right) \, = \, 1 \, - \, {\hat{r}} \left( {\hat{t}} \right) , \quad {\hat{X}} \left( {\hat{t}} \right) \, = \, {\hat{x}} \left( {\hat{t}} \right) \, {\mathcal {V}} \left( {\hat{t}} \right) , \\&{\hat{t}} \in \left[ 0, {\hat{T}} \right] . \end{aligned}\right. \end{aligned}$$

(18)

We will study two particular cases of this general model. First, as in Giordano et al. (2016), Yegorov et al. (2018), assume that the environmental conditions do not change over the observed time interval, either because the nutrient concentration s is approximately constant or because $s \gg K_M$ (when the substrate is available in excess). Then we consider the quantity

$$\begin{aligned} e_M \, {\mathop {=}\limits ^{\mathrm {def}}} \, k_M \, \frac{s}{K_M + s} \,\,\, \left[ \mathrm {h}^{-1} \right] \end{aligned}$$

(19)

as a constant environmental input and naturally suppose its positivity: $\, e_M = \mathrm {const} > 0$. Hence, the first formula in (13) is rewritten as

$$\begin{aligned} v_M(t) \, = \, e_M \, m(t) \, = \, e_M \, \cdot \, \left( \frac{1}{\beta } \, - \, r(t) \right) , \end{aligned}$$

(20)

and we arrive at the following model.

Definition 2.1

(Model 1: constant environmental conditions) In case $\, e_M = \mathrm {const} > 0, \,$ the system (18) is reduced to Model 1 defined by

$$\begin{aligned} \left\{ \begin{aligned}&\frac{d {\hat{p}} \left( {\hat{t}} \right) }{d {\hat{t}}} \,= \, E_M \, \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) \,\, - \,\, \left( 1 + {\hat{p}} \left( {\hat{t}} \right) \right) \, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \,\, \\&\qquad \qquad \,\,\, -\, k_1 \, \frac{{\hat{p}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) },\\&\frac{d {\hat{r}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, \left( u \left( {\hat{t}} \right) - {\hat{r}} \left( {\hat{t}} \right) \right) \, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) }, \\&\frac{d {\hat{x}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, k_1 \, \frac{{\hat{p}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) } \,\, - \,\, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, {\hat{x}} \left( {\hat{t}} \right) , \\&\frac{d {\mathcal {V}} \left( {\hat{t}} \right) }{d {\hat{t}}} \,= \, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, {\mathcal {V}} \left( {\hat{t}} \right) ,\\&{\hat{m}} \left( {\hat{t}} \right) \, = \, 1 \, - \, {\hat{r}} \left( {\hat{t}} \right) , \quad {\hat{X}} \left( {\hat{t}} \right) \, = \, {\hat{x}} \left( {\hat{t}} \right) \, {\mathcal {V}} \left( {\hat{t}} \right) ,\\&{\hat{t}} \in \left[ 0, {\hat{T}} \right] , \end{aligned}\right. \end{aligned}$$

(21)

with the additional dimensionless parameter

$$\begin{aligned} E_M \, {\mathop {=}\limits ^{\mathrm {def}}} \, \frac{e_M}{k_R}. \end{aligned}$$

(22)

Model 1 may describe fed-batch cultivation during which the nutrient concentration is either high enough or maintained at a certain level, so that nearly exponential bacterial growth is achieved (Cinar et al. 2003).

Definition 2.2

(Model 2: substrate depletion) In case $v_S \equiv 0$, substrates are only depleted and not replenished from the outside during the observed time interval. As a consequence, the system (18) is reduced to Model 2 defined by

$$\begin{aligned} \left\{ \begin{aligned}&\frac{d {\hat{s}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, -k_2 \, \frac{{\hat{s}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_2 + {\hat{s}} \left( {\hat{t}} \right) } \, \frac{{\mathcal {V}} \left( {\hat{t}} \right) }{{\mathcal {V}}_{\mathrm {ext}}}, \\&\frac{d {\hat{p}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, k_2 \, \frac{{\hat{s}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_2 + {\hat{s}} \left( {\hat{t}} \right) } \,\, - \,\, \left( 1 + {\hat{p}} \left( {\hat{t}} \right) \right) \, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \,\, \\&\qquad \qquad \quad \; -\, k_1 \, \frac{{\hat{p}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) }, \\&\frac{d {\hat{r}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, \left( u \left( {\hat{t}} \right) - {\hat{r}} \left( {\hat{t}} \right) \right) \, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) }, \\&\frac{d {\mathcal {V}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, \frac{{\hat{p}} \left( {\hat{t}} \right) {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, {\mathcal {V}} \left( {\hat{t}} \right) , \\&\frac{d {\hat{X}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, k_1 \, \frac{{\hat{p}} \left( {\hat{t}} \right) \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) } \, {\mathcal {V}} \left( {\hat{t}} \right) , \\&{\hat{m}} \left( {\hat{t}} \right) \, = \, 1 \, - \, {\hat{r}} \left( {\hat{t}} \right) , \\&{\hat{t}} \in \left[ 0, {\hat{T}} \right] . \end{aligned} \right. \end{aligned}$$

(23)

Model 2 is appropriate for describing batch cultivation (Cinar et al. 2003).

Note that, in Model 1, the equation for ${\hat{x}}$ is included instead of the equation for ${\hat{X}}$. As will be shown in the next section, this allows for a useful equivalent transformation of the product maximization criterion in Model 1, but is not appropriate for Model 2, due to the preservation of the equation for ${\hat{s}}$ in the latter model.

3 Statement of the optimal control problems with aggregated input

For Models 1 and 2, we are interested first in finding an aggregated control input u that maximizes the total product output, i.e., the total amount of metabolite produced. Recall from (2) that u is given by a combination of natural and synthetic mechanisms of growth control.

We fix the initial state as

$$\begin{aligned} \begin{aligned}&\displaystyle {\hat{p}}(0) \, = \, {\hat{p}}_0 \,> \, 0, \quad {\hat{r}}(0) \, = \, {\hat{r}}_0 \, \in \, (0, 1), \\&\displaystyle {\hat{X}}(0) \, = \, {\hat{X}}_0 \, \geqslant \, 0, \quad {\mathcal {V}}(0) \, = \, {\mathcal {V}}_0 \,> \, 0, \\&\displaystyle {\hat{s}}(0) \, = \, {\hat{s}}_0 \, > \, 0, \quad {\hat{x}}(0) \, = \, {\hat{x}}_0 \, = \, \dfrac{{\hat{X}}_0}{{\mathcal {V}}_0} \, \geqslant \, 0 \end{aligned} \end{aligned}$$

(24)

and recall the control constraint

$$\begin{aligned} u_{\min } \, \leqslant \, u \left( {\hat{t}} \right) \, \leqslant \, u_{\max } \quad \forall \, {\hat{t}} \in \left[ 0, {\hat{T}} \right] . \end{aligned}$$

(25)

Definition 3.1

(Product maximization problem) For the fixed initial state (24), the product maximization problem is specified by the criterion

$$\begin{aligned} {\hat{X}} \left( {\hat{T}} \right) \, - \, {\hat{X}}_0 \,\, \longrightarrow \,\, \max _{u(\cdot ) \, \in \, {\mathcal {U}}}, \end{aligned}$$

where ${\mathcal {U}}$ is the set of all admissible open-loop control strategies, which are Lebesgue measurable real-valued functions defined on the time interval $\left[ 0, {\hat{T}} \right]$ and satisfying the constraint (25). By using the dynamical equation for ${\hat{X}}$ (which is the same in Models 1 and 2), this criterion can be written as

$$\begin{aligned} {\hat{X}} \left( {\hat{T}} \right) \, - \, {\hat{X}}_0 \,\, = \,\, \int \limits _0^{{\hat{T}}} \, k_1 \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) } \, {\mathcal {V}} \left( {\hat{t}} \right) \, d {\hat{t}} \,\, \longrightarrow \,\, \max _{u(\cdot ) \, \in \, {\mathcal {U}}}. \end{aligned}$$

(26)

For later use, as a baseline for comparison, we also consider the biomass maximization problem (Giordano et al. 2016; Molenaar et al. 2009; Scott et al. 2010; Yegorov et al. 2018).

Definition 3.2

(Biomass maximization problem) For the fixed initial state (24), the biomass maximization problem is specified by the criterion

$$\begin{aligned} {\mathcal {V}} \left( {\hat{T}} \right) \, \longrightarrow \, \max _{u(\cdot ) \, \in \, {\mathcal {U}}}, \end{aligned}$$

where the control class ${\mathcal {U}}$ is the same as in Definition 3.1. By using the dynamical equation for ${\mathcal {V}}$ (which is the same in Models 1 and 2) and also the relation (17), this criterion can be written as

$$\begin{aligned} \int \limits _0^T \mu (t) \, dt \,\, = \,\, \int \limits _0^{{\hat{T}}} \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, d {\hat{t}} \,\, \longrightarrow \,\, \max _{u(\cdot ) \, \in \, {\mathcal {U}}}. \end{aligned}$$

(27)

Note that, in these two problems, the aggregated control input u is determined by (2) as the product of the natural growth control $\alpha$ and the synthetic growth control I. In practice, natural growth control is fixed, in the sense that the mechanisms underlying $\alpha$, which have been selected by evolution, are endogeneous and cannot be easily modified. The experimenter can only vary I, corresponding to induction of the synthesis of the gene expression machinery. In Sect. 5, we will refine the problems by distinguishing between natural and synthetic growth control. However, we remark that the solutions obtained by considering u as the control input have a clear interpretation: they provide the optimum that can be obtained independently of constraints imposed by natural growth control mechanisms. They thus form a gold standard against which more realistic strategies accessible in a biotechnological context can be compared.

The product maximization criterion (26) allows for an equivalent transformation. Since ${\hat{X}}$ does not appear in the expression for $d {\hat{X}} / d {\hat{t}}$, the initial value ${\hat{X}}_0$ can be chosen arbitrarily. Let us take ${\hat{X}}_0 > 0$. Then $\, {\hat{X}} \left( {\hat{t}} \right) > 0 \,$ and $\, {\hat{x}} \left( {\hat{t}} \right) \, = \, {\hat{X}} \left( {\hat{t}} \right) / {\mathcal {V}} \left( {\hat{t}} \right) \, > \, 0 \,$ for all $\, {\hat{t}} \in \left[ 0, {\hat{T}} \right] \,$ (recall that ${\mathcal {V}}_0 > 0$ due to (24), and, therefore, $\, {\mathcal {V}} \left( {\hat{t}} \right) > 0 \,$ on the whole observed time interval). Hence, one can write the relation

$$\begin{aligned} \ln \, {\hat{X}} \left( {\hat{T}} \right) \,\,&= \,\,\ln \, {\hat{x}} \left( {\hat{T}} \right) \,\, + \,\, \ln \, {\mathcal {V}} \left( {\hat{T}} \right) \,\, \nonumber \\= \,\,&\ln {\hat{x}}_0 \,\, + \,\, \int \limits _0^{{\hat{T}}} \, \frac{1}{{\hat{x}} \left( {\hat{t}} \right) } \, \frac{d {\hat{x}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, d {\hat{t}} \,\, \nonumber \\&+ \,\, \ln {\mathcal {V}}_0 \,\, + \,\, \int \limits _0^{{\hat{T}}} \, \frac{1}{{\mathcal {V}} \left( {\hat{t}} \right) } \, \frac{d {\mathcal {V}} \left( {\hat{t}} \right) }{d {\hat{t}}} \, d {\hat{t}} \,\, \nonumber \\= \,\,&\int \limits _0^{{\hat{T}}} \, \left( \frac{k_1}{{\hat{x}} \left( {\hat{t}} \right) } \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) } \,\, - \,\, \frac{{\hat{p}} \left( {\hat{t}} \right) \, {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \right) \, d {\hat{t}} \,\, \nonumber \\&+ \int \limits _0^{{\hat{T}}} \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, d {\hat{t}} \,\, + \,\, \ln {\hat{x}}_0 \,\, + \,\, \ln {\mathcal {V}}_0 \,\, \nonumber \\= \,\,&\int \limits _0^{{\hat{T}}} \, \frac{k_1}{{\hat{x}} \left( {\hat{t}} \right) } \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) } \, d {\hat{t}} \,\, + \,\, \ln {\hat{x}}_0 \,\, + \,\, \ln {\mathcal {V}}_0. \end{aligned}$$

(28)

This leads to an equivalence property that will be found useful below.

Property 3.3

If ${\hat{X}}_0 > 0$, the product maximization problem as stated in Definition 3.1 can be equivalently reformulated as

$$\begin{aligned} \int \limits _0^{{\hat{T}}} \, \frac{k_1}{{\hat{x}} \left( {\hat{t}} \right) } \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) } \, d {\hat{t}} \,\, \longrightarrow \,\, \max _{u(\cdot ) \, \in \, {\mathcal {U}}}. \end{aligned}$$

(29)

In what follows, when speaking about the product maximization criterion, we indiscriminately refer to (26) and (29). The condition ${\hat{X}}_0 > 0$ underlying the equivalence property can be imposed without loss of generality, and it will be assumed valid henceforth.

Assumption 3.4

${\hat{X}}_0 > 0$.

Even though the reasoning underlying the derivation of (29) applies to both Models 1 and 2, the proposed transformation is useful only for Model 1, where it becomes possible to exclude the equation for ${\mathcal {V}}$ from the system (22) when considering the product maximization criterion (26) or the integral representation of the biomass maximization criterion (27). For Model 2, the equation for ${\mathcal {V}}$ cannot simply be excluded from the system (23), because the equation for ${\hat{s}}$ includes ${\mathcal {V}}$.

The product maximization and biomass maximization problems for both Models 1 and 2 will be investigated in the next section.

4 Investigation of the optimal control problems with aggregated input

4.1 Model 1 (constant environmental conditions)

First, we consider Model 1. For the related product maximization problem, one can analyze the signs of the right-hand sides of the equations in (22) and thereby verify that

$$\begin{aligned} G \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\, \left\{ \left( {\hat{p}}, {\hat{r}}, {\hat{x}} \right) \, :\, {\hat{p}}> 0, \,\, 0< {\hat{r}} < 1, \,\, {\hat{x}} > 0 \right\} \end{aligned}$$

(30)

is a strongly invariant domain (Clarke et al. 1998, Chapter 4, §3). That is, for any admissible control function $u(\cdot ) \in {\mathcal {U}}$, the corresponding state trajectory of Model 1 in the space $\left( {\hat{p}}, {\hat{r}}, {\hat{x}} \right)$ cannot leave G if the initial state lies in G. For the biomass maximization problem, the equations for ${\hat{p}}, {\hat{r}}$ and also the criterion do not contain ${\hat{x}}$, i.e., ${\hat{x}}$ can be excluded from consideration, and the strongly invariant domain (30) therefore reduces to

$$\begin{aligned} G_1 \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\, \left\{ \left( {\hat{p}}, {\hat{r}} \right) \, :\, {\hat{p}} > 0, \,\, 0< {\hat{r}} < 1 \right\} . \end{aligned}$$

(31)

Furthermore, for any $\, \left( {\hat{p}}_0, {\hat{r}}_0, {\hat{x}}_0 \right) \, \in \, G \,$ and $u(\cdot ) \in {\mathcal {U}}$, the state variables ${\hat{p}}, {\hat{x}}$ in Model 1 admit the time-varying bounds

$$\begin{aligned} {\hat{p}} \left( {\hat{t}} \right) \, \leqslant \, {\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) , \quad {\hat{x}}_{\mathrm {low}} \left( {\hat{t}}; \, {\hat{x}}_0 \right) \, \leqslant \, {\hat{x}} \left( {\hat{t}} \right) \, \leqslant \, {\hat{x}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{x}}_0 \right) \quad \forall \, {\hat{t}} \in \left[ 0, {\hat{T}} \right] , \end{aligned}$$

(32)

where $\, {\hat{p}}_{\mathrm {up}} \left( \cdot ; \, {\hat{p}}_0 \right)$, $\, {\hat{x}}_{\mathrm {low}} \left( \cdot ; \, {\hat{x}}_0 \right)$, $\, {\hat{x}}_{\mathrm {up}} \left( \cdot ; \, {\hat{x}}_0 \right) \,$ are unique solutions to appropriately defined Cauchy problems for ordinary differential equations (see “Appendix A”).

The estimates (32) and strong invariance of the domain (30) ensure that, for any initial state coordinates $\, \left( {\hat{p}}_0, {\hat{r}}_0, {\hat{x}}_0 \right) \, \in \, G$, $\, {\mathcal {V}}_0 > 0 \,$ and control input $u(\cdot ) \in {\mathcal {U}}$, there exists a unique solution to the Cauchy problem (22), (24) and that this solution can be extended to the whole time interval $[0, +\infty )$. From the general existence result in Cesari (1983, §9.3) (see also Yong and Zhou 1999, Chapter 2, §5.1), it can be concluded that, for every fixed $\, \left( {\hat{p}}_0, {\hat{r}}_0, {\hat{x}}_0 \right) \, \in \, G, \,$ there exist optimal control functions in the class ${\mathcal {U}}$ for the product maximization and biomass maximization problems for Model 1.

Before investigating the dynamical optimal control problems, we provide the steady-state analysis.

4.1.1 Steady-state analysis for Model 1

For Model 1, we would like to find a steady state $\, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}}, {\hat{x}}^*_{\mathrm {opt}} \right) \, \in \, G \,$ for which the integrand in the product maximization criterion (29) takes its maximum value.

For any steady state $\, \left( {\hat{p}}^*, {\hat{r}}^*, {\hat{x}}^* \right) \, \in \, G \,$ of Model 1 such that

$$\begin{aligned} E_M \, - \, k_1 \, \frac{{\hat{p}}^*}{K_1 + {\hat{p}}^*} \,\, > \,\, 0, \end{aligned}$$

(33)

one has

$$\begin{aligned} \begin{aligned}&u^* \,\, = \,\, {\hat{r}}^* \,\, = \,\, \frac{E_M \, - \, k_1 \, \frac{{\hat{p}}^*}{K_1 + {\hat{p}}^*}}{E_M \, - \, k_1 \, \frac{{\hat{p}}^*}{K_1 + {\hat{p}}^*} \, + \, \left( 1 + {\hat{p}}^* \right) \, \frac{{\hat{p}}^*}{K + {\hat{p}}^*}} \,\, \in \,\, (0, 1), \\&{\hat{x}}^* \,\, = \,\, k_1 \, \frac{1 - {\hat{r}}^*}{{\hat{r}}^*} \, \frac{K + {\hat{p}}^*}{K_1 + {\hat{p}}^*} \,\, = \,\, \frac{k_1 \, \left( 1 + {\hat{p}}^* \right) \, {\hat{p}}^*}{\left( E_M \, - \, k_1 \, \frac{{\hat{p}}^*}{K_1 + {\hat{p}}^*} \right) \, \left( K_1 + {\hat{p}}^* \right) }, \end{aligned}\nonumber \\ \end{aligned}$$

(34)

i.e., the coordinates ${\hat{r}}^*, {\hat{x}}^*$ and control $u^*$ are represented as functions of ${\hat{p}}^*$, while the integrand in the product maximization criterion (29) can be written as

$$\begin{aligned} \frac{k_1}{{\hat{x}}^*} \, \frac{{\hat{p}}^* \, \left( 1 - {\hat{r}}^* \right) }{K_1 + {\hat{p}}^*} \,\,= & {} \,\, \frac{{\hat{p}}^* {\hat{r}}^*}{K + {\hat{p}}^*} \,\, \nonumber \\= & {} \,\, \frac{{\hat{p}}^*}{K + {\hat{p}}^*} \, \frac{E_M \, - \, k_1 \, \frac{{\hat{p}}^*}{K_1 + {\hat{p}}^*}}{E_M \, - \, k_1 \, \frac{{\hat{p}}^*}{K_1 + {\hat{p}}^*} \, + \, \left( 1 + {\hat{p}}^* \right) \, \frac{{\hat{p}}^*}{K + {\hat{p}}^*}}. \end{aligned}$$

(35)

The condition (33) guarantees the well-posedness and positivity of the expressions in (34) and (35). From (35), we arrive at the following property.

Property 4.1

At a steady state $\, \left( {\hat{p}}^*, {\hat{r}}^*, {\hat{x}}^* \right) \, \in \, G \,$ of Model 1 satisfying (33), the integrand in the product maximization criterion (29) coincides with the dimensionless growth rate (17), i.e., with the integrand in the biomass maximization criterion (27).

By (35), the steady-state production and growth rates can be determined as a function of ${\hat{p}}^*$. In order to find its maximum, we search for zeros of its derivative, which has the same sign as

$$\begin{aligned} \begin{aligned} \chi \left( {\hat{p}}^* \right) \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\,&\left( K + {\hat{p}}^* \right) ^2 \, \left( E_M \, - \, k_1 \, \frac{{\hat{p}}^*}{K_1 + {\hat{p}}^*} \, + \, \left( 1 + {\hat{p}}^* \right) \, \frac{{\hat{p}}^*}{K + {\hat{p}}^*} \right) ^2 \, \\&\cdot \, \frac{d}{d {\hat{p}}^*} \left( \frac{k_1}{{\hat{x}}^* \left( {\hat{p}}^* \right) } \, \frac{{\hat{p}}^* \, \left( 1 - {\hat{r}}^* \left( {\hat{p}}^* \right) \right) }{K_1 + {\hat{p}}^*} \right) \,\, \\ = \,\,&E_M \, \left( K E_M - \left( {\hat{p}}^* \right) ^2 \right) \, - \, 2 k_1 K E_M \, \frac{{\hat{p}}^*}{K_1 + {\hat{p}}^*} \, \\&+ \, k_1^2 K \, \frac{\left( {\hat{p}}^* \right) ^2}{\left( K_1 + {\hat{p}}^* \right) ^2} \, + \, k_1 \, \frac{\left( {\hat{p}}^* \right) ^3}{K_1 + {\hat{p}}^*} \, \\&- \, k_1 K_1 \, \left( 1 + {\hat{p}}^* \right) \, \frac{\left( {\hat{p}}^* \right) ^2}{\left( K_1 + {\hat{p}}^* \right) ^2}. \end{aligned} \end{aligned}$$

(36)

Solving $\, \chi \left( {\hat{p}}^* \right) = 0 \,$ yields ${\hat{p}}^*_{\mathrm {opt}}$. This problem can be reduced to searching for the roots of a fourth-order polynomial. The next assumption states the existence and uniqueness of such a root on the interval $\, 0 < {\hat{p}}^* \leqslant {\hat{p}}_{\mathrm {up}}^{\max } \left( {\hat{p}}_0 \right) , \,$ where

$$\begin{aligned} {\hat{p}}_{\mathrm {up}}^{\max } \left( {\hat{p}}_0 \right) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \max _{{\hat{t}} \, \in \, \left[ 0, {\hat{T}} \right] } \, {\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) \end{aligned}$$

(37)

with $\, {\hat{p}}_{\mathrm {up}} \left( \cdot ; \, {\hat{p}}_0 \right) \,$ appearing as the time-varying upper bound for ${\hat{p}}(\cdot )$ in (32), and ensures the maximum condition.

Assumption 4.2

It holds that

$$\begin{aligned} E_M \, - \, k_1 \, \frac{{\hat{p}}^*}{K_1 + {\hat{p}}^*} \,\, > \,\, 0 \quad \forall \, {\hat{p}}^* \in \left[ 0, \, {\hat{p}}_{\mathrm {up}}^{\max } \left( {\hat{p}}_0 \right) \right] \end{aligned}$$

(38)

(which ensures the well-posedness and positivity of (34) and (35)). Moreover, there exists a unique zero ${\hat{p}}^*_{\mathrm {opt}}$ of the function (36) on the interval $\, 0 \leqslant {\hat{p}}^* \leqslant {\hat{p}}_{\mathrm {up}}^{\max } \left( {\hat{p}}_0 \right) , \,$ and the following properties hold:

$$\begin{aligned} 0 \,&< \, {\hat{p}}^*_{\mathrm {opt}} \,< \, {\hat{p}}_{\mathrm {up}}^{\max } \left( {\hat{p}}_0 \right) , \\ \chi \left( {\hat{p}}^* \right) \,&> \, 0 \quad \forall \, {\hat{p}}^* \in \left[ 0, {\hat{p}}^*_{\mathrm {opt}} \right) , \\ \chi \left( {\hat{p}}^* \right) \, <&\, 0 \quad \forall \, {\hat{p}}^* \in \left( {\hat{p}}^*_{\mathrm {opt}}, \, {\hat{p}}_{\mathrm {up}}^{\max } \left( {\hat{p}}_0 \right) \right] , \\ u^*_{\mathrm {opt}} \,&= \, u^* \left( {\hat{p}}^*_{\mathrm {opt}} \right) \, \in \, (u_{\min }, u_{\max }). \end{aligned}$$

If analytical verification of Assumption 4.2 appears to be difficult, one can easily check it numerically.

Once ${\hat{p}}^*_{\mathrm {opt}}$ is obtained, the other components $\, {\hat{r}}^*_{\mathrm {opt}} = {\hat{r}}^* \left( {\hat{p}}^*_{\mathrm {opt}} \right)$, $\, {\hat{x}}^*_{\mathrm {opt}} = {\hat{x}}^* \left( {\hat{p}}^*_{\mathrm {opt}} \right) \,$ of the optimal steady state together with the corresponding constant control $\, u^*_{\mathrm {opt}} = u^* \left( {\hat{p}}^*_{\mathrm {opt}} \right) \,$ can be determined by (34).

In order to investigate the stability of the optimal steady state, we write the Jacobian matrix for the system of the first three equations in (22) (here the partial derivatives of the right-hand sides are taken with respect to ${\hat{p}}, {\hat{r}}, {\hat{x}}$, while u is treated as a constant parameter):

$$\begin{aligned} \begin{pmatrix} -\frac{{\hat{r}}}{K + {\hat{p}}} \, \left( {\hat{p}} + \frac{K \left( 1 + {\hat{p}} \right) }{K + {\hat{p}}} \right) \, - \, \frac{k_1 K_1 \, \left( 1 - {\hat{r}} \right) }{\left( K_1 + {\hat{p}} \right) ^2} \,\,\, &{} -E_M \, - \, \frac{\left( 1 + {\hat{p}} \right) {\hat{p}}}{K + {\hat{p}}} \, + \, \frac{k_1 {\hat{p}}}{K_1 + {\hat{p}}} \,\,\, &{} 0 \\ \frac{K {\hat{r}} \, \left( u - {\hat{r}} \right) }{\left( K + {\hat{p}} \right) ^2} &{} \frac{{\hat{p}} \, \left( u - 2 {\hat{r}} \right) }{K + {\hat{p}}} &{} 0 \\ \frac{k_1 K_1 \, \left( 1 - {\hat{r}} \right) }{\left( K_1 + {\hat{p}} \right) ^2} \, - \, \frac{K {\hat{r}} {\hat{x}}}{\left( K + {\hat{p}} \right) ^2} &{} -\frac{k_1 {\hat{p}}}{K_1 + {\hat{p}}} \, - \, \frac{{\hat{p}} {\hat{x}}}{K + {\hat{p}}} &{} -\frac{{\hat{p}} {\hat{r}}}{K + {\hat{p}}} \end{pmatrix}. \end{aligned}$$

For any steady state $\, \left( {\hat{p}}, {\hat{r}}, {\hat{x}} \right) \, \in \, G, \,$ we get $u = {\hat{r}}$, and, after substituting this equality, one can easily verify that the eigenvalues of the resulting matrix are real and negative. Hence, all such steady states including the optimal one are asymptotically stable nodes.

We summarize the obtained results in the form of a theorem.

Theorem 4.3

Let Assumptions 3.4 and 4.2 hold. Model 1 admits a unique optimal steady state $\, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}}, {\hat{x}}^*_{\mathrm {opt}} \right) \, \in \, G \,$ satisfying the inequality $\, 0 \leqslant {\hat{p}}^*_{\mathrm {opt}} \leqslant {\hat{p}}_{\mathrm {up}}^{\max } \left( {\hat{p}}_0 \right) \,$ and maximizing the integrand in the product maximization criterion (29). The first coordinate ${\hat{p}}^*_{\mathrm {opt}}$ is a unique zero of the function (36) on the interval $\, \left[ 0, \, {\hat{p}}_{\mathrm {up}}^{\max } \left( {\hat{p}}_0 \right) \right] , \,$ and the other coordinates together with the corresponding constant control can be determined by (34). Moreover, this steady state is an asymptotically stable node.

Due to Property 4.1 and Theorem 4.3, the pair $\left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right)$ also maximizes the integrand in the biomass criterion (27) over all steady states $\, \left( {\hat{p}}^*, {\hat{r}}^* \right) \in G_1 \,$ satisfying $\, 0 \leqslant {\hat{p}}^* \leqslant {\hat{p}}_{\mathrm {up}}^{\max } \left( {\hat{p}}_0 \right)$. In other words, for Model 1 (describing bacterial growth in a constant environment), product maximization and biomass maximization are identical at steady states.

Below we study product maximization and biomass maximization from a dynamical perspective.

4.1.2 Dynamical product maximization for Model 1

Now consider the dynamical product maximization problem for Model 1.

For the sake of convenience, introduce the new state variable

$$\begin{aligned} {\hat{y}} \, = \, {\hat{y}} \left( {\hat{t}} \right) \, {\mathop {=}\limits ^{\mathrm {def}}} \, \ln \, {\hat{x}} \left( {\hat{t}} \right) \end{aligned}$$

(39)

instead of ${\hat{x}} = {\hat{x}} \left( {\hat{t}} \right)$. Then the third equation in (22) is replaced with

$$\begin{aligned} \frac{d {\hat{y}} \left( {\hat{t}} \right) }{d {\hat{t}}} \,\, = \,\, k_1 \, e^{-{\hat{y}} \left( {\hat{t}} \right) } \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) } \, - \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) }, \end{aligned}$$

(40)

and the integrand in the product maximization criterion (29) transforms into the first term on the right-hand side of (40). The initial condition for (39) is

$$\begin{aligned} {\hat{y}}(0) \, = \, {\hat{y}}_0 \, = \, \ln \, {\hat{x}}_0. \end{aligned}$$

(41)

In optimal control theory, first-order necessary optimality conditions for open-loop control strategies are given by Pontryagin’s maximum principle or, in short, PMP (Pontryagin et al. 1964; Cesari 1983). For the product maximization problem for Model 1, PMP leads to the Hamiltonian

$$\begin{aligned}&H \left( {\hat{p}}, {\hat{r}}, {\hat{y}}, u, \psi _0, \psi _1, \psi _2, \psi _3 \right) \,\, = \,\, \left( E_M \, \left( 1 - {\hat{r}} \right) \, - \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \, \right. \nonumber \\&\quad \left. - \, k_1 \, \frac{{\hat{p}} \, \left( 1 - {\hat{r}} \right) }{K_1 + {\hat{p}}} \right) \, \psi _1 \,\, + \,\, \left( u - {\hat{r}} \right) \, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \, \psi _2 \,\, \nonumber \\&\quad + \,\, \left( k_1 \, e^{-{\hat{y}}} \, \frac{{\hat{p}} \, \left( 1 - {\hat{r}} \right) }{K_1 + {\hat{p}}} \, - \, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \right) \, \psi _3 \,\, - \,\, k_1 \, e^{-{\hat{y}}} \, \frac{{\hat{p}} \, \left( 1 - {\hat{r}} \right) }{K_1 + {\hat{p}}} \, \psi _0, \end{aligned}$$

(42)

and to the adjoint system

$$\begin{aligned} \left\{ \begin{aligned}&\psi _0 \equiv -1 \,\,\, \text{ or } \,\,\, \psi _0 \equiv 0,\\&\frac{d \psi _1 \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, -\frac{\partial H}{\partial {\hat{p}}} \left( {\hat{p}} \left( {\hat{t}} \right) , \, {\hat{r}} \left( {\hat{t}} \right) , \, {\hat{y}} \left( {\hat{t}} \right) , \, u \left( {\hat{t}} \right) , \, \psi _0, \, \psi _1 \left( {\hat{t}} \right) , \, \psi _2 \left( {\hat{t}} \right) , \, \psi _3 \left( {\hat{t}} \right) \right) \,\, \\&\qquad \qquad \,\, = \, K \, \frac{{\hat{r}} \left( {\hat{t}} \right) }{\left( K + {\hat{p}} \left( {\hat{t}} \right) \right) ^2} \, \left( \psi _1 \left( {\hat{t}} \right) \, \left( 1 + {\hat{p}} \left( {\hat{t}} \right) \right) \, + \, \psi _2 \left( {\hat{t}} \right) \, \left( {\hat{r}} \left( {\hat{t}} \right) \, - \, u \left( {\hat{t}} \right) \right) \, \right. \\&\qquad \qquad \qquad \, \left. + \, \psi _3 \left( {\hat{t}} \right) \right) \,\, + \,\, \psi _1 \left( {\hat{t}} \right) \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \,\, + \,\, k_1 K_1 \, \frac{1 - {\hat{r}} \left( {\hat{t}} \right) }{\left( K_1 + {\hat{p}} \left( {\hat{t}} \right) \right) ^2} \, \\&\qquad \qquad \qquad \, \cdot \, \left( \psi _1 \left( {\hat{t}} \right) \, - \, \left( \psi _3 \left( {\hat{t}} \right) - \psi _0 \right) \, e^{-{\hat{y}} \left( {\hat{t}} \right) } \right) ,\\&\frac{d \psi _2 \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, -\frac{\partial H}{\partial {\hat{r}}} \left( {\hat{p}} \left( {\hat{t}} \right) , \, {\hat{r}} \left( {\hat{t}} \right) , \, {\hat{y}} \left( {\hat{t}} \right) , \, u \left( {\hat{t}} \right) , \, \psi _0, \, \psi _1 \left( {\hat{t}} \right) , \, \psi _2 \left( {\hat{t}} \right) , \, \psi _3 \left( {\hat{t}} \right) \right) \,\, \\&\qquad \qquad \,\, = \, E_M \, \psi _1 \left( {\hat{t}} \right) \,\, + \,\, \frac{{\hat{p}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, \left( \psi _1 \left( {\hat{t}} \right) \, \left( 1 + {\hat{p}} \left( {\hat{t}} \right) \right) \, \right. \\&\qquad \qquad \qquad \, \left. + \, \psi _2 \left( {\hat{t}} \right) \, \left( 2 \, {\hat{r}} \left( {\hat{t}} \right) \, - \, u \left( {\hat{t}} \right) \right) \, + \, \psi _3 \left( {\hat{t}} \right) \right) \,\, - \,\, k_1 \, \frac{{\hat{p}} \left( {\hat{t}} \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) } \, \\&\qquad \qquad \qquad \, \cdot \, \left( \psi _1 \left( {\hat{t}} \right) \, - \, \left( \psi _3 \left( {\hat{t}} \right) - \psi _0 \right) \, e^{-{\hat{y}} \left( {\hat{t}} \right) } \right) , \\&\frac{d \psi _3 \left( {\hat{t}} \right) }{d {\hat{t}}} \, = \, -\frac{\partial H}{\partial {\hat{y}}} \left( {\hat{p}} \left( {\hat{t}} \right) , \, {\hat{r}} \left( {\hat{t}} \right) , \, {\hat{y}} \left( {\hat{t}} \right) , \, u \left( {\hat{t}} \right) , \, \psi _0, \, \psi _1 \left( {\hat{t}} \right) , \, \psi _2 \left( {\hat{t}} \right) , \, \psi _3 \left( {\hat{t}} \right) \right) \,\, \\&\qquad \qquad \,\, = \, \left( \psi _3 \left( {\hat{t}} \right) - \psi _0 \right) \, k_1 \, e^{-{\hat{y}} \left( {\hat{t}} \right) } \, \frac{{\hat{p}} \left( {\hat{t}} \right) \, \left( 1 - {\hat{r}} \left( {\hat{t}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) }, \\&{\hat{t}} \in \left[ 0, {\hat{T}} \right] , \end{aligned}\right. \end{aligned}$$

(43)

with appropriate boundary conditions, while an optimal control strategy should fulfill the Hamiltonian maximum condition almost everywhere on $\left[ 0, {\hat{T}} \right]$ (with respect to Lebesgue measure). The latter reduces to

$$\begin{aligned} u \left( {\hat{t}} \right) \,\, = \,\, {\left\{ \begin{array}{ll} u_{\min }, &{} \psi _2 \left( {\hat{t}} \right) \, < \, 0, \\ u_{\max }, &{} \psi _2 \left( {\hat{t}} \right) \, > \, 0. \end{array}\right. } \end{aligned}$$

(44)

Since there are no constraints on the terminal state at ${\hat{t}} = {\hat{T}}$, the terminal adjoint vector should satisfy

$$\begin{aligned} \psi _0 \, \equiv \, -1, \quad \psi _1 \left( {\hat{T}} \right) \, = \, \psi _2 \left( {\hat{T}} \right) \, = \, \psi _3 \left( {\hat{T}} \right) \, = \, 0. \end{aligned}$$

(45)

In general, if both initial and terminal states are fixed, the case $\psi _0 = 0$ cannot be excluded and there are no restrictions on the terminal adjoint vector.

An admissible process

$$\begin{aligned} \left( u(\cdot ), \, {\hat{p}}(\cdot ), \, {\hat{r}}(\cdot ), \, {\hat{y}}(\cdot ), \, \psi _0, \, \psi _1(\cdot ), \, \psi _2(\cdot ), \, \psi _3(\cdot ) \right) \end{aligned}$$

(46)

satisfying PMP is called extremal. It is called normal if $\psi _0 \ne 0$ (which holds in the studied case (45)) and abnormal if $\psi _0 = 0$.

Since the controlled system of Model 1 is autonomous (i.e., the right-hand sides of the related state equations depend on time only through the state and control variables), the Hamiltonian (42) is conserved along any extremal process (as also follows from the general formulation of PMP Cesari 1983; Pontryagin et al. 1964).

Property 4.4

The third adjoint equation in (43) directly implies

$$\begin{aligned} \begin{aligned}&\psi _3 \left( {\hat{t}} \right) \, - \, \psi _0 \,\, = \,\, \left( \psi _3 \left( {\hat{T}} \right) \, - \, \psi _0 \right) \,\, \\&\qquad \qquad \qquad \quad \quad \,\, \cdot \,\, \exp \left( -\int \limits _{{\hat{t}}}^{{\hat{T}}} k_1 \, e^{-{\hat{y}}(\xi )} \, \frac{{\hat{p}}(\xi ) \, \left( 1 - {\hat{r}}(\xi ) \right) }{K_1 + {\hat{p}}(\xi )} \, d \xi \right) \\&\forall \, {\hat{t}} \in \left[ 0, {\hat{T}} \right] . \end{aligned} \end{aligned}$$

(47)

Therefore, if $\, \psi _3 \left( {\hat{T}} \right) - \psi _0 \, > \, 0 \,$ (which holds for (45)), then the function $\, \psi _3(\cdot ) - \psi _0 \,$ is positive and strictly increasing everywhere on $\left[ 0, {\hat{T}} \right]$.

The Hamiltonian maximum condition (44) is written in terms of the switching function $\psi _2(\cdot )$. If $\psi _2(\cdot )$ vanishes over some time subinterval, the corresponding control and arc of the related extremal state trajectory are called singular (Gabasov and Kirillova 1982). Multiple fundamental works (Bonnard and Chyba 2003; Clark 1990; Schattler and Ledzewicz 2012, 2015; Zelikin and Borisov 1994, 2005) indicate the central role of singular control regimes for dynamical optimization problems arising in many application domains, such as economics, engineering, ecology, biology, and medical sciences.

If one consecutively differentiates the switching function $\, \psi _2 = \psi _2 \left( {\hat{t}} \right) \,$ along the system of the state and adjoint equations (22), (40), (43) and substitutes the singular arc condition $\, \psi _2 \left( {\hat{t}} \right) = 0, \,$ then the control $\, u = u \left( {\hat{t}} \right) \,$ may first occur only in the expression for an even-order derivative. In our case, this is the fourth-order derivative of the switching function. By checking the sign of the corresponding coefficient for the control, one can also conclude that the Kelley condition or, in other words, the generalized Legendre–Clebsch condition (Schattler and Ledzewicz 2012; Zelikin and Borisov 1994) (which is necessary for optimality of singular arcs) holds there in the form of a strict inequality. According to the theory of chattering control (Schattler and Ledzewicz 2012; Zelikin and Borisov 1994), a chattering phenomenon (involving an infinite number of bang-bang switchings between the control bounds $u_{\min }, u_{\max }$ on a finite time interval) should take place when entering or leaving a singular arc. Thus, we arrive at the following result.

Theorem 4.5

Let Assumption 3.4 hold. A singular arc in the product maximization problem for Model 1 can be entered or left only by chattering.

Complete characterization of the singular arcs by the direct analysis of the PMP boundary value problem (22), (24), (40), (41), (43)–(45) turns out to be rather complicated. However, in contrast to what was previously obtained for biomass maximization problems without heterologous metabolite production (Giordano et al. 2016; Yegorov et al. 2018), the current problem does not allow for singular arcs with steady coordinates ${\hat{p}}$ and ${\hat{r}}$.

Theorem 4.6

Let Assumption 3.4 and the condition (38) in Assumption 4.2 hold. A singular arc in the product maximization problem for Model 1 cannot have steady coordinates ${\hat{p}}$ and ${\hat{r}}$, that is, the corresponding solution to the PMP system (22), (24), (40), (41), (43), (45) cannot satisfy $\, d {\hat{p}} \left( {\hat{t}} \right) / d {\hat{t}} \, = \, d {\hat{r}} \left( {\hat{t}} \right) / d {\hat{t}} \, = \, \psi _2 \left( {\hat{t}} \right) \, = \, 0 \,$ on a subinterval of $\left[ 0, {\hat{T}} \right]$.

Theorem 4.6 is proved in “Appendix B”.

For illustrating the above results, we numerically solve the product maximization problem for Model 1 by using the software package BOCOP (Bonnans et al. 2017).¹ The parameter values

$$\begin{aligned}&\displaystyle u_{\min } \, = \, 0, \quad u_{\max } \, = \, 1, \end{aligned}$$

(48)

$$\begin{aligned}&\displaystyle \beta \, = \, 0.003 \,\, \mathrm {L} \ \mathrm {g}^{-1}, \quad k_R \, = \, 3.6 \,\, \mathrm {h}^{-1}, \quad K_R \, = \, 1 \,\, \mathrm {g} \ \mathrm {L}^{-1}, \end{aligned}$$

(49)

$$\begin{aligned}&\displaystyle e_M \, = \, 3.6 \,\, \mathrm {h}^{-1} \end{aligned}$$

(50)

are chosen in line with Giordano et al. (2016), and they are completed with reasonable values for the parameters characterizing the production pathway:

$$\begin{aligned} k_X \, = \, 0.5 \,\, \mathrm {h}^{-1}, \quad K_X \, = \, 1 \,\, \mathrm {g} \ \mathrm {L}^{-1}. \end{aligned}$$

(51)

The dimensionless parameters in Model 1 are then determined by (16). In order to clearly observe the dynamics, the initial coordinates ${\hat{p}}_0, {\hat{r}}_0$ are taken sufficiently far away from the optimal steady state components ${\hat{p}}^*_{\mathrm {opt}}$, ${\hat{r}}^*_{\mathrm {opt}}$. More precisely, we set

$$\begin{aligned} \left( {\hat{p}}_0, {\hat{r}}_0 \right) \,\, = \,\, \left. \left( {\hat{p}}^*_{\mathrm {opt}, \, k_1 \, = \, 0}, \, {\hat{r}}^*_{\mathrm {opt}, \, k_1 \, = \, 0} \right) \right| _{e_M \, = \, 0.72 \,\, \mathrm {h}^{-1}}, \end{aligned}$$

(52)

where $\, \left. \left( {\hat{p}}^*_{\mathrm {opt}, \, k_1 \, = \, 0}, \, {\hat{r}}^*_{\mathrm {opt}, \, k_1 \, = \, 0} \right) \right| _{e_M \, = \, 0.72 \,\, \mathrm {h}^{-1}} \,$ is the optimal steady state for the biomass maximization problem of Giordano et al. (2016) (whose dynamical system can be obtained from the first two equations of (22) by taking $k_1 = 0$ and $u \equiv \alpha$) with the lower environmental input $\, e_M \, = \, 0.72 \,\, \mathrm {h}^{-1} \,$ and with the other parameters as in (48), (49). This can be interpreted as a nutrient upshift after transferring from a poor environment to a richer one. The initial coordinate ${\hat{x}}_0 = e^{{\hat{y}}_0}$ is selected as

$$\begin{aligned} {\hat{x}}_0 \, = \, {\hat{x}}^*_{\mathrm {opt}} \end{aligned}$$

(53)

(it can in fact be chosen arbitrarily, because the initial product amount ${\hat{X}}_0$ can be fixed as any positive number, as was discussed in Sect. 3). Assumption 4.2 (including conditions on functions of single variables with values in bounded intervals) has been numerically verified for these data.

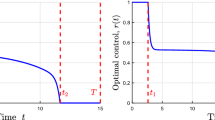
Figures 2 and 3 indicate the corresponding numerical simulation results, for the time horizons ${\hat{T}} = 15$ and ${\hat{T}} = 50$, respectively. In BOCOP, we set the number of time steps to 5000 and the tolerance to $10^{-6}$, and we use the sixth-order Lobatto III C discretization rule (Bonnans et al. 2017). Note also that BOCOP supplies smoothing techniques for handling chattering control. One can see that the singular arcs are entered and left by chattering, as expected from Theorem 4.5. With the increase of the time horizon ${\hat{T}}$, the absolute and also relative duration of the singular control regime increases, and the singular arcs closer approach the optimal steady state $\, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}}, {\hat{x}}^*_{\mathrm {opt}} \right) , \,$ without completely coinciding with the latter, as per Theorem 4.6. Leaving the singular control regime some time before the final instant is typical for finite-horizon optimal resource allocation problems in different areas (Akhmetzhanov et al. 2011; Grigorieva and Khailov 2007; Yegorov et al. 2015, 2017a). It should be noted, however, that even for the small horizon ${\hat{T}} = 15$ (Fig. 2), and a fortiori for larger finite horizons (Fig. 3), the final chattering regime gives only a slight relative addition ($< 1\%$) to the total product output in comparison with the practically more convenient strategy of extending the singular regime until the end of the observed time interval.

Fig. 2

The optimal control input and state variables for the product maximization problem for Model 1 computed by using BOCOP. The parameter values and initial conditions are given by (48)–(53). The time horizon is taken as ${\hat{T}} = 15$

Fig. 3

The optimal control input and state variables for the product maximization problem for Model 1 computed by using BOCOP. The parameter values and initial conditions are given by (48)–(53). The time horizon is taken as ${\hat{T}} = 50$

4.1.3 Dynamical biomass maximization for Model 1

The dynamics of the optimal control inputs, as shown in Figs. 2 and 3, resembles the bang-bang-singular strategies for the biomass maximization problems studied in Giordano et al. (2016), Yegorov et al. (2017b, 2018). This motivates an optimal control analysis under the biomass maximization criterion of Definition 3.2, in order to determine if biomass maximization is a good approximation of product maximization. As a further motivation, we remind that, by virtue of Property 4.1, the integrands in the product maximization and biomass maximization criteria coincide with each other at steady states. As a consequence, the optimal steady-state coordinates $\left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right)$ for the product maximization problem also lead to the maximal steady-state biomass production. The singular arcs in Figs. 2 and 3, which make up most of the optimal trajectories, are close to the optimal steady state, thus suggesting that biomass maximization may approximate product maximization.

First, it is useful to construct the third adjoint component $\psi _3(\cdot )$ for the product maximization problem in Model 1, based on the formula (47), terminal conditions (45) and the optimal state trajectory computed via BOCOP. The related graphs in the two cases ${\hat{T}} = 15$ and ${\hat{T}} = 50$ are shown in Fig. 4. One can see that, in reverse time, this function decreases by starting at $\, \psi _3 \left( {\hat{T}} \right) = 0 \,$ and approaching the number $\psi _0 = -1$, which is done relatively fast if ${\hat{T}}$ is large enough.

Fig. 4

The third adjoint component $\, \psi _3 = \psi _3 \left( {\hat{t}} \right) \,$ for the product maximization problem in Model 1, constructed from the formula (47), terminal conditions (45) and the optimal state trajectory computed via BOCOP. The parameter values and initial conditions are given by (48)–(53), and the two cases ${\hat{T}} = 15$ and ${\hat{T}} = 50$ are considered

In view of the above, we formally set $\, \psi _3 \left( {\hat{t}} \right) \equiv \psi _0 \,$ in the adjoint system (43) for the product maximization problem. Then, after introducing the new notations $\eta _0, \eta _1, \eta _2$ instead of $\psi _0, \psi _1, \psi _2$, respectively, we arrive at the following two-dimensional adjoint system:

$$\begin{aligned} \left\{ \begin{aligned}&\eta _0 \equiv -1 \,\,\, \text{(normal } \text{ case) } \,\,\, \text{ or } \,\,\, \eta _0 \equiv 0 \,\,\, \text{(abnormal } \text{ case), } \\&\frac{d \eta _1 \left( {\hat{t}} \right) }{d {\hat{t}}} \,\, = \,\, K \, \frac{{\hat{r}} \left( {\hat{t}} \right) }{\left( K + {\hat{p}} \left( {\hat{t}} \right) \right) ^2} \, \left( \eta _1 \left( {\hat{t}} \right) \, \left( 1 + {\hat{p}} \left( {\hat{t}} \right) \right) \, \right. \\&\qquad \qquad \quad \quad \left. + \, \eta _2 \left( {\hat{t}} \right) \, \left( {\hat{r}} \left( {\hat{t}} \right) \, - \, u \left( {\hat{t}} \right) \right) \, + \, \eta _0 \right) \,\, \\&\qquad \qquad \quad \quad + \,\, \eta _1 \left( {\hat{t}} \right) \, \left( \frac{{\hat{p}} \left( {\hat{t}} \right) \, {\hat{r}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, + \, k_1 K_1 \, \frac{1 - {\hat{r}} \left( {\hat{t}} \right) }{\left( K_1 + {\hat{p}} \left( {\hat{t}} \right) \right) ^2} \right) , \\&\frac{d \eta _2 \left( {\hat{t}} \right) }{d {\hat{t}}} \,\, = \,\, E_M \, \eta _1 \left( {\hat{t}} \right) \,\, + \,\, \frac{{\hat{p}} \left( {\hat{t}} \right) }{K + {\hat{p}} \left( {\hat{t}} \right) } \, \left( \eta _1 \left( {\hat{t}} \right) \, \left( 1 + {\hat{p}} \left( {\hat{t}} \right) \right) \, \right. \\&\qquad \qquad \quad \quad \left. + \, \eta _2 \left( {\hat{t}} \right) \, \left( 2 \, {\hat{r}} \left( {\hat{t}} \right) \, - \, u \left( {\hat{t}} \right) \right) \, + \, \eta _0 \right) \,\, \\&\qquad \qquad \quad \quad - \,\, \eta _1 \left( {\hat{t}} \right) \, k_1 \, \frac{{\hat{p}} \left( {\hat{t}} \right) }{K_1 + {\hat{p}} \left( {\hat{t}} \right) }, \\&{\hat{t}} \in \left[ 0, {\hat{T}} \right] . \end{aligned} \right. \end{aligned}$$

(54)

The latter is the same as the adjoint system obtained by formulating PMP for the biomass maximization problem for Model 1, where the state can be reduced to only two variables ${\hat{p}}$ and ${\hat{r}}$.

Similarly to the formulations in Yegorov et al. (2018, Subsection 2.2) regarding biomass maximization problems for self-replicator models without a heterologous metabolic pathway, we reasonably exclude the final chattering regime for the biomass maximization problem for Model 1 by imposing the terminal constraint

$$\begin{aligned} \left( {\hat{p}} \left( {\hat{T}} \right) , \, {\hat{r}} \left( {\hat{T}} \right) \right) \, = \, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right) . \end{aligned}$$

(55)

Note that the time horizon ${\hat{T}} \in (0, +\infty )$ is fixed and taken large enough in order to guarantee the existence of admissible trajectories satisfying this constraint.

The following existence result can be established similarly to Yegorov et al. (2018, Theorem 5.1).

Theorem 4.7

Let Assumptions 3.4 and 4.2 hold. There exists an optimal open-loop control strategy in the biomass maximization problem for Model 1 under the terminal constraint (55) if the time horizon ${\hat{T}}$ is sufficiently large.

The minimum suitable horizon ${\hat{T}}$ in Theorem 4.7 depends on the initial state $\, \left( {\hat{p}}_0, {\hat{r}}_0 \right) \, \in \, G_1$. A heuristic way of selecting an appropriate horizon is to integrate the first two equations in (21) with $u \equiv u^*_{\mathrm {opt}}$ numerically until a sufficiently small neighborhood of $\left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right)$ is reached and then to take ${\hat{T}}$ somewhat greater than the final time of the integration.

The next theorem can be proved by using PMP similarly to the results of Yegorov et al. (2018, Section 6).

Theorem 4.8

Let Assumptions 3.4 and 4.2 hold. Consider the biomass maximization problem for Model 1 under the terminal constraint (55). Abnormal extremal processes in this problem do not allow for singular regimes. Any singular arc of a normal extremal process in this problem stays at the optimal steady state $\left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right)$ and can be entered or left only by chattering. For a related chattering arc, bang-bang switchings from $u = u_{\max }$ to $u = u_{\min }$ (in forward time) occur only in the domain

$$\begin{aligned} \left\{ \left( {\hat{p}}, {\hat{r}} \right) \, \in \, G_1 \, :\, {\hat{r}} \, > \, {\hat{r}}^* \left( {\hat{p}} \right) \right\} , \end{aligned}$$

(56)

and switchings in the opposite direction occur only in the domain

$$\begin{aligned} \left\{ \left( {\hat{p}}, {\hat{r}} \right) \, \in \, G_1 \, :\, {\hat{r}} \, < \, {\hat{r}}^* \left( {\hat{p}} \right) \right\} , \end{aligned}$$

(57)

where the function $\, {\hat{r}}^* = {\hat{r}}^* \left( {\hat{p}} \right) \,$ is defined by (34).

Furthermore, we have developed a numerical method for constructing the switching curve of the optimal feedback control law in the biomass maximization problem for Model 1 under the terminal constraint (55). The related description and illustrations are given in “Appendix C”. As in Yegorov et al. (2018), we exclude abnormal extremal processes (with $\eta _0 \equiv 0$) from consideration due to the fact that they do not allow for singular regimes (as mentioned in Theorem 4.8) and therefore do not admit a clear biological interpretation.

Figures 5 and 6 show the results of solving the biomass maximization problem for Model 1 under the terminal constraint (55) by means of BOCOP, with the same parameters and initial states as in the previous subsection. For comparison, the results for the product maximization problem from Figs. 2 and 3 are also reproduced. In agreement with our theoretical results, the state variables ${\hat{p}}, {\hat{r}}$ in Figs. 5 and 6 reach the optimal steady-state coordinates ${\hat{p}}^*_{\mathrm {opt}}$, ${\hat{r}}^*_{\mathrm {opt}}$ by chattering and then stay in the singular regime until the final time. The second chattering arc does not appear by virtue of (55).

Fig. 5

The optimal control input and state variables for the biomass maximization problem for Model 1 under the terminal constraint (55), computed by using BOCOP (black dashed curves). The parameter values and initial conditions are given by (48)–(53). The time horizon is taken as ${\hat{T}} = 15$. The solutions of the corresponding product maximization problem for Model 1 (Fig. 2) are also indicated for comparison (gray solid curves)

Fig. 6

The optimal control input and state variables for the biomass maximization problem for Model 1 under the terminal constraint (55), computed by using BOCOP (black dashed curves). The parameter values and initial conditions are given by (48)–(53). The time horizon is taken as ${\hat{T}} = 50$. The solutions of the corresponding product maximization problem for Model 1 (Fig. 3) are also indicated for comparison (gray solid curves)

Figure 7 compares the values of the integral

$$\begin{aligned} \int \limits _0^{{\hat{t}}} \, \frac{k_1}{{\hat{x}}(\xi )} \, \frac{{\hat{p}}(\xi ) \, \left( 1 - {\hat{r}}(\xi ) \right) }{K_1 + {\hat{p}}(\xi )} \, d \xi , \end{aligned}$$

(58)

which serves as a characteristic of the product output over the time interval $\left[ 0, {\hat{t}} \right]$ according to Property 3.3. The integral is computed from the numerically constructed optimal solutions of the product maximization and biomass maximization problems. The amount of X produced by the optimal control strategy for the biomass maximization problem, even when imposing the terminal constraint (55), is seen to be very close to that obtained for the product maximization problem. This confirms that, for Model 1, where the environmental conditions remain constant, biomass maximization results in a good approximation of product maximization. This can be intuitively understood by the fact that the amount of metabolite X produced is somewhat proportional to the exponentially growing amount of biomass. As a consequence, when an unlimited amount of substrate is available, it becomes profitable to produce as much biomass as possible, even if this leads to a lower metabolite production per unit of biomass, since most of the substrate is utilized for the synthesis of biomass (and not product).

Fig. 7

Comparison of the values of the product output characteristic (58) for the product maximization problem for Model 1 (gray solid curves), and for the biomass maximization problem for Model 1 under the terminal constraint (55) (black dashed curves). The functions are approximated from the numerical solutions indicated in Figs. 2, 3, 5, 6. The parameter values are given by (48)–(53), and the two cases ${\hat{T}} = 15$ and ${\hat{T}} = 50$ are considered

4.2 Model 2 (substrate depletion)

In biotechnological problems of practical interest, substrates are expensive and not available in unlimited amounts. Rather, the problem consists in converting a limited amount of substrate into the maximum amount of metabolite of interest within a given time interval. A priori, one would expect that, in order to maximize metabolite production over the time interval, a trade-off has to be found in promoting either biomass synthesis or product synthesis. This can be understood by considering the extreme of high metabolic machinery content, enhancing precursor and product synthesis, but leading eventually to low growth. In this case, the little biomass produced does not allow all substrate to be converted into the metabolite of interest within the observed time interval. On the other hand, promoting growth does not necessarily maximize the yield of conversion of the available substrate into the metabolite of interest.

In order to obtain the optimal trade-off, we study the product maximization problem for Model 2 given by Definitions 2.2 and 3.1. In Model 2, contrary to Model 1, the dynamics of the substrate and volume variables have to be taken into account, and the transformation of the optimization criterion in Property 3.3 is therefore not useful. This makes it very difficult to derive analytical results via PMP, and we hence resort directly to numerical optimization by means of BOCOP.

In addition to the parameter values (48), (49), (51) and the initial state coordinates (52) already introduced for Model 1, we need to specify the parameters $k_M, K_M$ characterizing the macroreaction converting the substrate into precursors, as well as the initial state coordinates $s_0, X_0, {\mathcal {V}}_0$ and the external volume ${\mathcal {V}}_{\mathrm {ext}}$. For consistency, we set the initial uptake rate $\, k_M s_0 \, / \, (K_M + s_0) \,$ equal to the value (50) of the lumped environmental parameter chosen for Model 1. Bearing in mind the variable and parameter transformations (16), we take $\, k_M \, = \, 1.2 \, k_R$, $\, K_M \, = \, 0.1 / \beta , \,$ i.e.,

$$\begin{aligned} k_2 \, = \, 1.2, \quad K_2 \, = \, 0.1, \end{aligned}$$

(59)

and specify the remaining initial conditions as

$$\begin{aligned} {\hat{s}}_0 \, = \, 0.5, \quad \ln \, {\mathcal {V}}_0 \, = \, 0 \,\, \mathrm {L}, \quad {\hat{X}}_0 \, = \, 0 \,\, \mathrm {L}. \end{aligned}$$

(60)

We also consider the three different time horizons ${\hat{T}} = 15$, ${\hat{T}} = 20$, and ${\hat{T}} = 50$. The logarithm of the external volume is selected as

$$\begin{aligned} \ln \, {\mathcal {V}}_{\mathrm {ext}} \, = \, 8 \,\, \mathrm {L} \end{aligned}$$

(61)

in the cases ${\hat{T}} = 15$, ${\hat{T}} = 20$, and as

$$\begin{aligned} \ln \, {\mathcal {V}}_{\mathrm {ext}} \, = \, 22 \,\, \mathrm {L} \end{aligned}$$

(62)

for ${\hat{T}} = 50$. Note that a larger ${\mathcal {V}}_{\mathrm {ext}}$ for the same $\, {\hat{s}}_0 \, = \, \beta S_0 / {\mathcal {V}}_{\mathrm {ext}} \,$ leads to a higher initial substrate amount $S_0$.

The solutions of the product maximization problem for Model 2 are shown in Figs. 8, 9 and 10. For comparison, the solutions of the corresponding biomass maximization problem are plotted as well. One can see that, while the control input profiles for the product maximization and biomass maximization problems are quite similar in the beginning, they start to diverge after some time. For the product maximization problem, the intermediate singular regime is left noticeably earlier, and u is thereafter set to 0 until the end of the observed time interval. That is, the synthesis of the gene expression machinery (R) is shut off, and the nutrients are used only for the synthesis of the metabolic machinery (M) and for producing the metabolite of interest (X). Put in a schematic way, the optimal control strategy for the product maximization problem seems to consist in the first phase of maximal growth followed by the second phase of maximal production. The difference in the control input profiles also leads to different state dynamics. In particular, for product maximization, the concentration ${\hat{r}}$ of the gene expression machinery decreases due to growth dilution after u is set to 0. As a consequence, the total amount of biomass generated is lower than for biomass maximization, but the total production is higher.

We thus conclude that, whereas biomass maximization is a good approximation of product maximization for Model 1, this is not true for Model 2. In the latter case, the arrest of the gene expression machinery (and therefore growth) via the external control input leads to a sizeable increase in metabolite production.

Fig. 8

The optimal control input and state variables for the product maximization problem for Model 2, computed by using BOCOP (gray solid curves). The parameter values and initial conditions are given by (48), (49), (51), (52), (59)–(61). The time horizon is taken as ${\hat{T}} = 15$. We also indicate the solutions of the corresponding biomass maximization problem for Model 2, computed by using BOCOP (black dashed curves). For convenience, the logarithmic scales $\, \ln \, {\mathcal {V}} \,$ and $\, \ln \, \left( 1 + {\hat{X}} \right) \,$ are used for illustrating the dynamics of the structural volume and product output

Fig. 9

The optimal control input and state variables for the product maximization problem for Model 2, computed by using BOCOP (gray solid curves). The parameter values and initial conditions are given by (48), (49), (51), (52), (59)–(61). The time horizon is taken as ${\hat{T}} = 20$. We also indicate the solutions of the corresponding biomass maximization problem for Model 2, computed by using BOCOP (black dashed curves). For convenience, the logarithmic scales $\, \ln \, {\mathcal {V}} \,$ and $\, \ln \, \left( 1 + {\hat{X}} \right) \,$ are used for illustrating the dynamics of the structural volume and product output

Fig. 10

The optimal control input and state variables for the product maximization problem for Model 2, computed by using BOCOP (gray solid curves). The parameter values and initial conditions are given by (48), (49), (51), (52), (59), (60), (62). The time horizon is taken as ${\hat{T}} = 50$. We also indicate the solutions of the corresponding biomass maximization problem for Model 2, computed by using BOCOP (black dashed curves). For convenience, the logarithmic scales $\, \ln \, {\mathcal {V}} \,$ and $\, \ln \, \left( 1 + {\hat{X}} \right) \,$ are used for illustrating the dynamics of the structural volume and product output

5 Dynamical product maximization with natural and synthetic growth controls

We have thus far considered models in which both natural and synthetic growth controls are aggregated into a single input (as discussed in Sect. 3). This is clearly an idealized situation, since we have implicitly assumed that the synthetic growth control I can completely override the natural growth control $\alpha$. In reality, the two are expected to interfere, which may therefore reduce the efficacy of the efforts to reorient resources from growth to metabolite production. Following (2), we henceforth assume that the two effects are multiplicative, i.e.,

$$\begin{aligned} u \left( {\hat{t}} \right) \, = \, I \left( {\hat{t}} \right) \, \alpha \left( {\hat{t}} \right) . \end{aligned}$$

(63)

How can we model natural growth control? In Giordano et al. (2016), it was shown for the self-replicator in Fig. 1a (without a heterologous pathway and without external growth control) that a certain discontinuous feedback strategy leads to a reasonable approximation of the optimal policy for biomass maximization (see Fig. 11a). This so-called on-off strategy maps values of ${\hat{p}}$ and ${\hat{r}}$ into values of $\alpha$:

$$\begin{aligned} \alpha \left( {\hat{t}} \right) \,\, = \,\, \alpha \left( {\hat{p}} \left( {\hat{t}} \right) , \, {\hat{r}} \left( {\hat{t}} \right) \right) . \end{aligned}$$

(64)

Moreover, the on-off strategy was shown to resemble the action of a major regulatory system involved in growth control in E. coli, the ppGpp system (Bosdriesz et al. 2015). In this section, we introduce Model 3, a version of Model 2 with the aggregated control (63) and with the natural feedback control (64) constructed from the on-off strategy of Giordano et al. (2016) (see Fig. 11b).

Fig. 11

Self-replicator models of bacterial growth and metabolite production taking into account natural and synthetic growth controls. a Original self-replicator model from Fig. 1a, including natural feedback growth control following the on-off strategy proposed by Giordano et al. (2016). This on-off strategy mimics the effect of ppGpp regulation in E. coli (Bosdriesz et al. 2015). b Idem for the extended self-replicator model from Fig. 1b, with the pathway for metabolite production. Growth control in these self-replicators involves a combination of natural growth control via $\alpha$ and synthetic control via the external inducer I

The self-replicator model, for which the on-off strategy was originally proposed (under the hypothesis that the self-replicators have evolved to maximize the production of biomass Giordano et al. 2016), does not include the heterologous (non-natural) pathway for the production of metabolite X (see Fig. 11a). As a consequence, the steady state with the maximal growth rate and the corresponding constant control input differ between the models with and without the heterologous pathway. Production of X can be completely shut off by setting $k_1 = 0$, and we therefore use the notations ${\hat{p}}^*_{\mathrm {opt}, \, k_1 = 0}$, ${\hat{r}}^*_{\mathrm {opt}, \, k_1 = 0}$, and $\alpha ^*_{\mathrm {opt}, \, k_1 = 0}$ for the optimal steady state and for the corresponding control in the model of Giordano et al. (2016) without metabolite production.

Model 3 also revisits another hypothesis, namely that the external signal can be switched on and off at will. This may be possible for optogenetic regulation of gene expression (Milias-Argeitis et al. 2016; Olson and Tabor 2014), but does not hold for the chemical induction system used by Izard et al. (2015). We make the simplifying assumption that RNA polymerase synthesis is initially fully active, and then switched off at a time instant ${\hat{t}}_{\mathrm {sw}} \in \left[ 0, {\hat{T}} \right]$. This reduces the range of control strategies considered, but allows us to answer the question to which extent the approach implemented by Izard et al. (2015), where a phase with maximal induction of RNA polymerase expression is followed by a phase with no induction, can provide a reasonable approximation of the optimal solutions obtained in Sect. 4.2.

Hence, we define Model 3 and the corresponding product maximization problem as follows.

Definition 5.1

(Model 3: natural and synthetic growth controls) Consider the system of equations (23) defining Model 2. Model 3 extends them by adopting (63), (64) with

$$\begin{aligned} \begin{aligned}&I \left( {\hat{t}} \right) \,\, = \,\, {\left\{ \begin{array}{ll} I_0, &{} {\hat{t}} \in \left[ 0, {\hat{t}}_{\mathrm {sw}} \right) , \\ 0, &{} {\hat{t}} \in \left[ {\hat{t}}_{\mathrm {sw}}, {\hat{T}} \right] , \end{array}\right. } \\&{\hat{t}}_{\mathrm {sw}} \in \left[ 0, {\hat{T}} \right] , \quad I_0 \in \left[ 0, I_{\max } \right] , \end{aligned} \end{aligned}$$

(65)

and

$$\begin{aligned} \begin{aligned}&\alpha \left( {\hat{p}}, {\hat{r}} \right) \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\, {\left\{ \begin{array}{ll} 0, &{} {\hat{r}} \, > \, g \left( {\hat{p}} \right) , \\ 1, &{} {\hat{r}} \, < \, g \left( {\hat{p}} \right) , \\ \alpha ^*_{\mathrm {opt}, \, k_1 \, = \, 0}, &{} \left( {\hat{p}}, {\hat{r}} \right) \, = \, \left( {\hat{p}}^*_{\mathrm {opt}, \, k_1 \, = \, 0}, \, {\hat{r}}^*_{\mathrm {opt}, \, k_1 \, = \, 0} \right) , \end{array}\right. } \\&\forall \, \left( {\hat{p}}, {\hat{r}} \right) \, \in \, G_1, \end{aligned} \end{aligned}$$

(66)

where $\, {\hat{p}}^*_{\mathrm {opt}, \, k_1 = 0}$, $\, {\hat{r}}^*_{\mathrm {opt}, \, k_1 = 0}$, $\, \alpha ^*_{\mathrm {opt}, \, k_1 = 0} \,$ are as mentioned above, and

$$\begin{aligned} g \left( {\hat{p}} \right) \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\, \frac{{\hat{p}}}{{\hat{p}} \, + \, K \, \frac{1 + {\hat{p}}}{K + {\hat{p}}}} \quad \forall \, {\hat{p}} > 0, \end{aligned}$$

(67)

in line with Giordano et al. (2016, Appendix S1).

The use of Model 3 instead of Model 2 requires a modification of the statement of the optimization problem as well, since the control input is no longer $u(\cdot )$, but consists of the pair of scalars $\left( {\hat{t}}_{\mathrm {sw}}, I_0 \right)$, that is, the time at which synthesis of the gene expression machinery is switched off and the initial induction level, respectively.

Definition 5.2

(Revised product maximization problem) Adopt the representations (63)–(67). For the fixed initial state (24), the revised product maximization problem is specified by the criterion

$$\begin{aligned} {\hat{X}} \left( {\hat{T}} \right) \, \longrightarrow \, \max _{\left( {\hat{t}}_{\mathrm {sw}}, I_0 \right) \,\, \in \,\, \left[ 0, {\hat{T}} \right] \, \times \, [0, I_{\max }]}. \end{aligned}$$

Here optimization is performed over the switch-off times of the gene expression machinery and over the initial induction levels.

While there is not much hope for solving the revised product maximization problem for Model 3 analytically, the numerical solution can easily be obtained by testing different combinations of ${\hat{t}}_{\mathrm {sw}}$ and $I_0$ on a two-dimensional grid for the rectangle $\, \left[ 0, {\hat{T}} \right] \times [0, I_{\max }]$. We have developed a dedicated C++ program to this end.² We set the maximal induction level and the grid stepsizes to

$$\begin{aligned} I_{\max } \, = \, 1, \quad \varDelta {\hat{t}}_{\mathrm {sw}} \, = \, 0.01, \quad \varDelta I_0 \, = \, 0.01. \end{aligned}$$

(68)

In order to reduce errors in numerical integration of the dynamical equations (23), we replace the discontinuous law (66) with its continuously differentiable approximation determined by

$$\begin{aligned} \begin{aligned}&\alpha \left( {\hat{p}}, {\hat{r}} \right) \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\, {\left\{ \begin{array}{ll} 0, &{} {\hat{r}} \, \geqslant \, g \left( {\hat{p}} \right) \, + \, \varepsilon , \\ 1, &{} {\hat{r}} \, \leqslant \, g \left( {\hat{p}} \right) \, - \, \varepsilon , \\ \varphi \left( \dfrac{{\hat{r}} \, - \, g \left( {\hat{p}} \right) }{\varepsilon } \right) , &{} \left| {\hat{r}} \, - \, g \left( {\hat{p}} \right) \right| \, \leqslant \, \varepsilon , \end{array}\right. } \\&\forall \, \left( {\hat{p}}, {\hat{r}} \right) \, \in \, G_1, \\ \end{aligned} \end{aligned}$$

(69)

where $\varepsilon > 0$ is a sufficiently small parameter, and the function $\, \varphi \, :\, [-1, 1] \rightarrow [0, 1] \,$ is selected as the third-order polynomial

$$\begin{aligned} \varphi (x) \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\, \dfrac{x^3}{4} \, - \, \dfrac{3 x}{4} \, + \, \dfrac{1}{2} \quad \forall \, x \in [-1, 1] \end{aligned}$$

(70)

satisfying

$$\begin{aligned} \varphi (-1) \, = \, 1, \quad \varphi (1) \, = \, 0, \quad \varphi '(-1) \, = \, \varphi '(1) \, = \, 0. \end{aligned}$$

We take

$$\begin{aligned} \varepsilon \, = \, 5 \cdot 10^{-3}. \end{aligned}$$

(71)

The other parameters and initial states are chosen as in Sect. 4.2 for Model 2. In particular, the three time horizons ${\hat{T}} = 15$, ${\hat{T}} = 20$, ${\hat{T}} = 50$ are considered, and the external volume ${\mathcal {V}}_{\mathrm {ext}}$ is determined by (61) in the cases ${\hat{T}} = 15$, ${\hat{T}} = 20$, and by (62) for ${\hat{T}} = 50$.

Fig. 12

The optimal control input and state variables for the (revised) product maximization problem for Model 3 (blue curves). The parameter values and initial conditions are given by (49), (51), (52), (59)–(61), (68), (71). The time horizon is ${\hat{T}} = 15$. The dynamics of the natural feedback growth control strategy approximated by (69) is illustrated as well. We also indicate the solutions of the corresponding product maximization and biomass maximization problems for Model 2, taken from Fig. 8 (gray solid and black dashed curves, respectively) (color figure online)

Fig. 13

The optimal control input and state variables for the (revised) product maximization problem for Model 3 (blue curves). The parameter values and initial conditions are given by (49), (51), (52), (59)–(61), (68), (71). The time horizon is ${\hat{T}} = 20$. The dynamics of the natural feedback growth control strategy approximated by (69) is illustrated as well. We also indicate the solutions of the corresponding product maximization and biomass maximization problems for Model 2, taken from Fig. 9 (gray solid and black dashed curves, respectively) (color figure online)

Fig. 14

The optimal control input and state variables for the (revised) product maximization problem for Model 3 (blue curves). The parameter values and initial conditions are given by (49), (51), (52), (59), (60), (62), (68), (71). The time horizon is ${\hat{T}} = 50$. The dynamics of the natural feedback growth control strategy approximated by (69) is illustrated as well. We also indicate the solutions of the corresponding product maximization and biomass maximization problems for Model 2, taken from Fig. 10 (gray solid and black dashed curves, respectively) (color figure online)

The corresponding numerical results for the (revised) product maximization problem for Model 3 are shown in Figs. 12, 13 and 14 (blue curves). For comparison, the solutions of the product maximization and biomass maximization problems for Model 2 (Figs. 8, 9, 10) are also indicated (gray solid and black dashed curves, respectively). First, one can see that the profiles of the aggregated control strategy u for the product maximization problems for Models 2 and 3 look similar to each other. The major qualitative difference here is that leaving the singular regime at $\, {\hat{t}} = {\hat{t}}_{\mathrm {sw}, \, \mathrm {opt}} \,$ no longer involves chattering in case of Model 3. However, the effect of this difference on the optimal amount of metabolite X produced is negligible. Second, the optimal value $I_{0, \, \mathrm {opt}}$ in Model 3 equals $I_{\max }$, meaning that the optimal strategy essentially consists in a growth phase followed by a production phase, like for the product maximization problem for Model 2. We conclude from these results that, for the purpose of product maximization, synthetic growth control can effectively override natural growth control, and that even the simple induction strategy, consisting of a single shift from maximal induction to zero induction of synthesis of the gene expression machinery, like in Izard et al. (2015), leads to a near-optimal solution.

6 Discussion

The functioning of microbial cells on the molecular level involves complex regulatory networks controlling the biochemical reactions responsible for, among other things, the transformation of external substrates into precursor metabolites, and the conversion of the precursors into proteins (biomass). The understanding of these regulatory networks in control-theoretical terms has become well-established (Iglesias and Ingalls 2010; Sontag 2005). For example, the robustness of the response of microbial cells to environmental perturbations has been identified with the operation of integral feedback controllers on the molecular level (Yi et al. 2000, see El-Samad et al. 2005; Sauro 2017 for other examples). Moreover, control theory has the potential of guiding the reengineering and control of regulatory networks for biotechnological or biomedical purposes (Iglesias and Ingalls 2010; Vecchio et al. 2016), notably by exploiting advances in synthetic biology to rewire interactions in the network (Khalil and Collins 2010). An example is a theoretical study of the dynamical control of metabolic pathways by a synthetic gene circuit (Oyarzún and Stan 2013, see also Chaves and Gouzé 2011; de Hijas-Liste et al. 2014; Waldherr et al. 2015).

In this paper, we have studied the reallocation of cellular resources via external control of the gene expression machinery from the perspective of dynamical optimization. While inspired by previous works based on the use of self-replicator models for the analysis of microbial growth (Ewald et al. 2017; Giordano et al. 2016; Molenaar et al. 2009; Pavlov and Ehrenberg 2013; Scott et al. 2014; van den Berg et al. 1998; Weiße et al. 2015; Yegorov et al. 2018), we have focused on engineered rather than naturally evolved resource allocation strategies. In particular, we have developed extended self-replicator models that include a pathway for the production of a metabolite of biotechnological interest as well as a synthetic circuit for externally controlling the expression of RNA polymerase. The motivation for this system has come from a recent experimental work on a synthetic growth switch in E. coli (Izard et al. 2015), in which growth was arrested by externally shutting off the expression of RNA polymerase, thus enabling the passive redirection of incoming nutrient fluxes from biomass synthesis to the production of a metabolite of interest.

Three model variants of this extended self-replicator have been considered. Model 1 assumes that substrate availability is unlimited and that the substrate concentration in the medium is essentially constant over the time interval considered. This is not the case for Model 2, which takes into account the diminution of the substrate concentration due to the consumption of the limited substrate supply by the growing bacterial population. Whereas Models 1 and 2 both assume that the synthesis of the gene expression machinery is fully determined by the external control signal, Model 3 makes the more realistic assumption that this control interferes with natural feedback growth control mechanisms. A simple representation of the latter mechanisms, proposed by Giordano et al. (2016), has been included in Model 3 as an extension of Model 2. The model variants have been studied by a combination of analytical and computational techniques to find the external control signal leading to either product or biomass maximization.

When resources are unlimited (Model 1), essentially the same amount of product is obtained by product maximization and biomass maximization. In other words, external growth arrest by switching off synthesis of the gene expression machinery does not bring any advantage in this case. Since resources are unlimited, there is no penalty for spending resources on biomass, so that a population with a high exponential growth rate will be more productive than a population with a low exponential growth rate. This is not true in the case of limited resources (Model 2), where in order to maximize the amount of product obtained, for a given duration of the production process, a trade-off needs to be found between high productivity (total rate of conversion of substrate into product, depending on the size of the population) and high yield (efficiency of the conversion of substrate into product). This yield/productivity trade-off is well-known in metabolic engineering (Venayak et al. 2015). The optimal solution for product maximization in case of Model 2 consists of a two-stage procedure: a first stage of maximal biomass production followed by a second stage of maximal product synthesis. Imposing this two-stage procedure on Model 3 shows no significant decrease in the amount of product obtained, suggesting that the efficacity of external growth control is not affected by natural feedback growth control, at least for the self-replicator models considered here.

The self-replicator models used in this paper are very simplified representations of the biological processes taking place in living cells, as discussed in Sect. 2. Among other things, the models neglect protein degradation, lump macromolecules into only two classes of proteins, and disregard cell division. Some of the simplifications could affect the qualitative nature of the optimal control solutions found. However, the conclusion that the two-stage scheme of biomass maximization followed by product maximization is optimal corresponds well with established practice in biotechnology (Anesiadis et al. 2008; Venayak et al. 2015). As a matter of fact, the experimental test of the growth switch by Izard et al. (2015) also followed this scheme, in that bacteria from a preculture grown under maximal induction of RNA polymerase expression (growth phase) were rediluted into the same medium without inducer and thus without RNA polymerase expression (production phase), increasing the yield of glycerol production from glucose. The results of the present study suggest a way to optimize this procedure, namely to choose the time of redilution (or equivalently, the redilution factor) in such a way that the amount of glycerol produced over a given time interval is maximal.

In the case of biomass maximization for the original self-replicator model in Fig. 1a (Giordano et al. 2016), the addition of protein degradation did not fundamentally change the conclusions of the dynamical optimal control analysis for physiological temperatures (Yegorov et al. 2018). This may not always be the case for the extended self-replicators in this paper, especially for long time intervals of metabolite production, since enzyme degradation will decrease the maximum possible rate of metabolite production. As a consequence, periodic strategies with more than one on/off switch of the gene expression machinery may become relevant, allowing a restart of the gene expression machinery when enzyme degradation becomes a limiting factor. Such repeated on/off switches would be much facilitated by light induction rather than chemical induction, as it requires the ability to decrease and not only to increase the inducer signal.

These dynamical scenarios raise interesting optimal control problems, but also questions about the actual implementation of the strategies. Optimal open-loop strategies as provided by the analysis in this paper may inform the design of more robust quasi-optimal closed-loop strategies, by engineering adaptive feedback from real-time observations of the process behavior (growth rate, amount of gene expression machinery R) to the temporal induction of the gene expression machinery. Some interesting work on feedback control at the interface of control engineering and synthetic biology has appeared in recent years (Fracassi et al. 2016; Milias-Argeitis et al. 2016; Uhlendorf et al. 2012).

Appendices

Appendix A: Time-varying bounds for state variables in Model 1

As can be directly verified, the unique solutions to the following Cauchy problems can serve as time-varying bounds (32) for the state variables ${\hat{p}}, {\hat{x}}$ in Model 1:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{d {\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) }{d {\hat{t}}} \, = \, \max _{\rho \, \in \, [0, 1]} \left( \left( k_1 \, \frac{{\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) }{K_1 + {\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) } \,\, \right. \right. \\&\qquad \left. \left. - \,\, \left( 1 + {\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) \right) \, \frac{{\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) }{K + {\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) } \,\, - \,\, E_M \right) \, \rho \right) \,\, \\&\qquad \, + \,\, E_M \,\, - \,\, k_1 \, \frac{{\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) }{K_1 + {\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) }, \quad {\hat{t}} \in \left[ 0, {\hat{T}} \right] , \\&{\hat{p}}_{\mathrm {up}} \left( 0; \, {\hat{p}}_0 \right) \, = \, {\hat{p}}_0, \end{aligned}\right. \end{aligned}$$

(72)

$$\begin{aligned} \left\{ \begin{aligned}&\frac{d {\hat{x}}_{\mathrm {low}} \left( {\hat{t}}; \, {\hat{x}}_0 \right) }{d {\hat{t}}} \,= \, -\frac{{\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) }{K + {\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) } \, {\hat{x}}_{\mathrm {low}} \left( {\hat{t}}; \, {\hat{x}}_0 \right) , \quad {\hat{t}} \in \left[ 0, {\hat{T}} \right] , \\&{\hat{x}}_{\mathrm {low}} \left( 0; \, {\hat{x}}_0 \right) \, = \, {\hat{x}}_0, \end{aligned}\right. \end{aligned}$$

(73)

$$\begin{aligned} \left\{ \begin{aligned}&\frac{d {\hat{x}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{x}}_0 \right) }{d {\hat{t}}} \, = \, k_1 \, \frac{{\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) }{K_1 + {\hat{p}}_{\mathrm {up}} \left( {\hat{t}}; \, {\hat{p}}_0 \right) }, \quad {\hat{t}} \in \left[ 0, {\hat{T}} \right] , \\&{\hat{x}}_{\mathrm {up}} \left( 0; \, {\hat{x}}_0 \right) \, = \, {\hat{x}}_0. \end{aligned}\right. \end{aligned}$$

(74)

Although the right-hand side of the system (72) is nonlinear, one can see that it satisfies the sublinear growth property (see, e.g., (Markley 2004, §2.3)) due to the boundedness of the fractions involved. This ensures the extendability of the unique solution of the Cauchy problem to the whole observed time interval. The existence, uniqueness, and extendability of the solution of (72) obviously imply those for (73) and (74).

Appendix B: Proof of Theorem 4.6

Consider an extremal process (46) and a time subinterval where

$$\begin{aligned} \psi _2 \, = \, \frac{d \psi _2}{d {\hat{t}}} \, = \, 0 \end{aligned}$$

(75)

(a singular regime). Assume that ${\hat{p}}$ and ${\hat{r}}$ are steady, i.e.,

$$\begin{aligned} \frac{d {\hat{p}}}{d {\hat{t}}} \, = \, \frac{d {\hat{r}}}{d {\hat{t}}} \, = \, 0 \end{aligned}$$

(76)

(${\hat{x}}$ and ${\hat{y}}$ are not necessarily steady). It suffices to show that these conditions lead to $\, \psi _3 - \psi _0 \equiv 0, \,$ because the latter contradicts with (45). Note that, in line with Property 4.4, the fulfillment of the equality $\, \psi _3 - \psi _0 = 0 \,$ for at least one instant implies its fulfillment in the whole considered time interval.

The condition (38) and the first state equation in (22) yield

$$\begin{aligned}&E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \,\,> \,\, E_M \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \,\, > \,\, 0, \nonumber \\&\quad {\hat{r}} \,\, = \,\, \frac{E_M \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}}}{E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}}} \,\, \in \,\, (0, 1). \end{aligned}$$

(77)

From the second adjoint equation in (43) and the condition (75), one obtains

$$\begin{aligned} \psi _1 \,\, = \,\,&-\frac{1}{E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}}} \, \nonumber \\&\cdot \, \left( (\psi _3 - \psi _0) \, \left( \frac{{\hat{p}}}{K + {\hat{p}}} \, + \, k_1 \, e^{-{\hat{y}}} \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \right) \, + \, \psi _0 \, \frac{{\hat{p}}}{K + {\hat{p}}} \right) . \end{aligned}$$

(78)

The third adjoint equation in (43) and the equation (40) lead to

$$\begin{aligned}&\frac{d}{d {\hat{t}}} \, (\psi _3 - \psi _0) \,\, = \,\, \frac{d \psi _3}{d {\hat{t}}} \,\, = \,\, (\psi _3 - \psi _0) \, k_1 \, e^{-{\hat{y}}} \, \frac{{\hat{p}} \, \left( 1 - {\hat{r}} \right) }{K_1 + {\hat{p}}}, \nonumber \\&\frac{d}{d {\hat{t}}} \left( (\psi _3 - \psi _0) \, e^{-{\hat{y}}} \right) \,\, = \,\, (\psi _3 - \psi _0) \, e^{-{\hat{y}}} \, \left( k_1 \, e^{-{\hat{y}}} \, \frac{{\hat{p}} \, \left( 1 - {\hat{r}} \right) }{K_1 + {\hat{p}}} \, \right. \nonumber \\&\qquad \left. - \, k_1 \, e^{-{\hat{y}}} \, \frac{{\hat{p}} \, \left( 1 - {\hat{r}} \right) }{K_1 + {\hat{p}}} \, + \, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \right) \,\, = \,\, (\psi _3 - \psi _0) \, e^{-{\hat{y}}} \, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}}. \end{aligned}$$

(79)

From (76), (78) and (79), one arrives at

$$\begin{aligned} \begin{aligned} \frac{d \psi _1}{d {\hat{t}}} \,\,&= \,\, -\frac{1}{E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}}} \, \left( (\psi _3 - \psi _0) \, k_1 \, e^{-{\hat{y}}} \, \right. \\&\quad \left. \cdot \, \frac{{\hat{p}} \, \left( 1 - {\hat{r}} \right) }{K_1 + {\hat{p}}} \, \frac{{\hat{p}}}{K + {\hat{p}}} \,\, + \,\, (\psi _3 - \psi _0) \, e^{-{\hat{y}}} \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \right) \,\, \\&= \,\, -\frac{(\psi _3 - \psi _0) \, k_1 \, e^{-{\hat{y}}}}{E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}}} \, \frac{{\hat{p}}^2}{\left( K + {\hat{p}} \right) \, \left( K_1 + {\hat{p}} \right) }, \\ \frac{d^2 \psi _1}{d {\hat{t}}^2} \,\,&= \,\, \frac{d \psi _1}{d {\hat{t}}} \, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \,\, \\&= \,\, -\frac{(\psi _3 - \psi _0) \, k_1 \, e^{-{\hat{y}}}}{E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}}} \, \frac{{\hat{p}}^3 \, {\hat{r}}}{\left( K + {\hat{p}} \right) ^2 \, \left( K_1 + {\hat{p}} \right) }. \end{aligned} \end{aligned}$$

(80)

On the other hand, the first adjoint equation in (43) and the condition (75) give

$$\begin{aligned} \begin{aligned} \frac{d \psi _1}{d {\hat{t}}} \,\,&= \,\, \left( \left( K \, \frac{1 + {\hat{p}}}{\left( K + {\hat{p}} \right) ^2} \, + \, \frac{{\hat{p}}}{K + {\hat{p}}} \right) \, {\hat{r}} \,\, + \,\, \frac{k_1 K_1}{\left( K_1 + {\hat{p}} \right) ^2} \, \left( 1 - {\hat{r}} \right) \right) \, \psi _1 \,\, \\&\quad - \left( k_1 K_1 \, e^{-{\hat{y}}} \, \frac{1 - {\hat{r}}}{\left( K_1 + {\hat{p}} \right) ^2} \,\, - \,\, K \, \frac{{\hat{r}}}{\left( K + {\hat{p}} \right) ^2} \right) \, (\psi _3 - \psi _0) \,\, \\&\quad + \psi _0 \, K \, \frac{{\hat{r}}}{\left( K + {\hat{p}} \right) ^2}, \end{aligned} \end{aligned}$$

which implies

$$\begin{aligned}&\frac{d^2 \psi _1}{d {\hat{t}}^2} \,\, - \,\, \left( \left( K \, \frac{1 + {\hat{p}}}{\left( K + {\hat{p}} \right) ^2} \, + \, \frac{{\hat{p}}}{K + {\hat{p}}} \right) \, {\hat{r}} \,\, + \,\, \frac{k_1 K_1}{\left( K_1 + {\hat{p}} \right) ^2} \, \left( 1 - {\hat{r}} \right) \right) \, \frac{d \psi _1}{d {\hat{t}}} \,\, \nonumber \\&\quad = \,\, -k_1 K_1 \, \frac{1 - {\hat{r}}}{\left( K_1 + {\hat{p}} \right) ^2} \, (\psi _3 - \psi _0) \, e^{-{\hat{y}}} \, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \,\, \nonumber \\&\qquad \,\, + \, K \, \frac{{\hat{r}}}{\left( K + {\hat{p}} \right) ^2} \, (\psi _3 - \psi _0) \, k_1 \, e^{-{\hat{y}}} \, \frac{{\hat{p}} \, \left( 1 - {\hat{r}} \right) }{K_1 + {\hat{p}}} \,\, \nonumber \\&\quad = \,\, \frac{{\hat{p}} \, {\hat{r}} \, \left( 1 - {\hat{r}} \right) }{\left( K + {\hat{p}} \right) \, \left( K_1 + {\hat{p}} \right) } \, (\psi _3 - \psi _0) \, k_1 \, e^{-{\hat{y}}} \, \left( \frac{K}{K + {\hat{p}}} \, - \, \frac{K_1}{K_1 + {\hat{p}}} \right) \end{aligned}$$

(81)

due to (76) and (79). By substituting (80) into (81), one gets

$$\begin{aligned} \begin{aligned}&-\frac{(\psi _3 - \psi _0) \, k_1 \, e^{-{\hat{y}}}}{E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}}} \, \frac{{\hat{p}}^2}{\left( K + {\hat{p}} \right) \, \left( K_1 + {\hat{p}} \right) } \, \\&\qquad \quad \cdot \, \left( \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \,\, - \,\, \left( \left( K \, \frac{1 + {\hat{p}}}{\left( K + {\hat{p}} \right) ^2} \, + \, \frac{{\hat{p}}}{K + {\hat{p}}} \right) \, {\hat{r}} \,\, + \,\, \frac{k_1 K_1}{\left( K_1 + {\hat{p}} \right) ^2} \, \left( 1 - {\hat{r}} \right) \right) \right) \,\, \\&\quad \quad = \,\, \frac{{\hat{p}} \, {\hat{r}} \, \left( 1 - {\hat{r}} \right) }{\left( K + {\hat{p}} \right) \, \left( K_1 + {\hat{p}} \right) } \, (\psi _3 - \psi _0) \, k_1 \, e^{-{\hat{y}}} \, \left( \frac{K}{K + {\hat{p}}} \, - \, \frac{K_1}{K_1 + {\hat{p}}} \right) . \end{aligned} \end{aligned}$$

This is simplified to

$$\begin{aligned}&\frac{(\psi _3 - \psi _0) \, {\hat{p}}}{E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}}} \, \left( K \, \frac{1 + {\hat{p}}}{\left( K + {\hat{p}} \right) ^2} \, {\hat{r}} \,\, + \,\, \frac{k_1 K_1}{\left( K_1 + {\hat{p}} \right) ^2} \, \left( 1 - {\hat{r}} \right) \right) \,\, \nonumber \\&\qquad = \,\, {\hat{r}} \, \left( 1 - {\hat{r}} \right) \, (\psi _3 - \psi _0) \, \left( \frac{K}{K + {\hat{p}}} \, - \, \frac{K_1}{K_1 + {\hat{p}}} \right) \end{aligned}$$

(82)

and trivially holds for $\, \psi _3 - \psi _0 = 0$.

Now let $\, \psi _3 - \psi _0 \ne 0$. Then, after substituting (77) into (82) and canceling $\psi _3 - \psi _0$, one consecutively derives

$$\begin{aligned} \begin{aligned}&\frac{{\hat{p}}}{\left( E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \right) ^2} \, \left( K \, \frac{1 + {\hat{p}}}{\left( K + {\hat{p}} \right) ^2} \, \left( E_M \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \right) \,\, \right. \\&\qquad \,\,\, \left. + \,\, \frac{k_1 K_1}{\left( K_1 + {\hat{p}} \right) ^2} \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \right) \,\, \\&\quad = \,\, \frac{\left( E_M \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \right) \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}}}{\left( E_M \, + \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \right) ^2} \, \left( \frac{K}{K + {\hat{p}}} \, - \, \frac{K_1}{K_1 + {\hat{p}}} \right) , \\&\frac{K}{K + {\hat{p}}} \, \left( E_M \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \right) \,\, + \,\, {\hat{p}} \, \frac{k_1 K_1}{\left( K_1 + {\hat{p}} \right) ^2} \,\, \\&\quad = \,\, \left( E_M \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \right) \, \left( \frac{K}{K + {\hat{p}}} \, - \, \frac{K_1}{K_1 + {\hat{p}}} \right) , \\&{\hat{p}} \, \frac{k_1 K_1}{\left( K_1 + {\hat{p}} \right) ^2} \,\, = \,\, - \left( E_M \, - \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \right) \, \frac{K_1}{K_1 + {\hat{p}}}, \\&k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}} \,\, = \,\, -E_M \, + \, k_1 \, \frac{{\hat{p}}}{K_1 + {\hat{p}}}, \\&E_M \, = \, 0. \end{aligned} \end{aligned}$$

The obtained contradiction with $E_M > 0$ completes the proof. $\square$

Appendix C: Optimal feedback control in the biomass maximization problem for Model 1 under the terminal constraint (55)

In this section, we adopt Assumptions 3.4, 4.2 and consider the biomass maximization problem for Model 1 under the terminal constraint (55).

First, we develop a numerical method for constructing the chattering switching curve $\Sigma$ of the optimal feedback control law in the space of the state variables ${\hat{p}}, {\hat{r}}$. A similar approach was proposed in (Yegorov et al. 2018, Section 7) regarding biomass maximization problems for self-replicator models without a heterologous metabolic pathway.

The chattering arcs enter the singular regime at the optimal steady state $\left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right)$. The latter divides $\Sigma$ into two subcurves $\Sigma _0$ and $\Sigma _1$, so that bang-bang switchings from $u = u_{\max }$ to $u = u_{\min }$ (in forward time) occur only on $\Sigma _0$ and switchings in the opposite direction occur only on $\Sigma _1$. We do not include the optimal steady state in $\Sigma _0$ and $\Sigma _1$. According to Theorem 4.8, $\Sigma _0$ lies in the set (56), and $\Sigma _1$ is contained in the set (57). The optimal feedback strategy equals $u_{\min }$ on the upper side of $\Sigma$ and $u_{\max }$ on the lower side of $\Sigma$. These properties can be seen in Fig. 15.

Since u does not explicitly appear in the first equation of (22), the first component of the corresponding velocity vector field is continuous regardless of u. From

$$\begin{aligned} \left. \frac{d {\hat{p}}}{d {\hat{t}}} \right| _{\small {(22)}, \,\, \left( {\hat{p}}, {\hat{r}} \right) \, = \, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right) } \,\, = \,\, 0, \end{aligned}$$

(83)

one arrives at the hypothesis that the tangent line to $\Sigma$ at $\left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right)$ is unique and vertical (as also observed in Fig. 15). For a rigorous verification, one can use the following property (whose general formulation can be found in (Naumov 2003)): if the directions of the vectors

$$\begin{aligned}&\left. \left( \dfrac{d {\hat{p}}}{d {\hat{t}}}, \, \dfrac{d {\hat{r}}}{d {\hat{t}}} \right) \right| _{\small {(22)}, \,\, \left( {\hat{p}}, {\hat{r}} \right) \, = \, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right) , \,\, u \, = \, u_{\min }}, \\&\left. \left( \dfrac{d {\hat{p}}}{d {\hat{t}}}, \, \dfrac{d {\hat{r}}}{d {\hat{t}}} \right) \right| _{\small {(22)}, \,\, \left( {\hat{p}}, {\hat{r}} \right) \, = \, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right) , \,\, u \, = \, u_{\max }} \end{aligned}$$

coincide with each other, then this is also the direction of the unique tangent line to $\Sigma$ at $\left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right)$. Therefore, the latter is vertical by virtue of (83). Note that such tangent lines are also vertical for optimal chattering regimes in the well-known Fuller and Marshal problems (Schattler and Ledzewicz 2012; Zelikin and Borisov 1994).

Thus, one can choose a sufficiently small $\delta > 0$ such that, in the closed neighborhood

$$\begin{aligned} \left\{ \left( {\hat{p}}, {\hat{r}} \right) \, \in \, {\mathbb {R}}^2 \, :\, \left( {\hat{p}} - {\hat{p}}^*_{\mathrm {opt}} \right) ^2 \, + \, \left( {\hat{r}} - {\hat{r}}^*_{\mathrm {opt}} \right) ^2 \, \leqslant \, \delta ^2 \right\} \end{aligned}$$

(84)

of the optimal steady state, it is reasonable to approximate the switching curve $\Sigma$ as the vertical line segment

$$\begin{aligned} L_{\delta } \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\, \left\{ \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}} \right) \, :\, \left| {\hat{r}} - {\hat{r}}^*_{\mathrm {opt}} \right| \, \leqslant \, \delta \right\} . \end{aligned}$$

(85)

Consider an extremal process

$$\begin{aligned} \left( u(\cdot ), \, {\hat{p}}(\cdot ), \, {\hat{r}}(\cdot ), \, \eta _0, \, \eta _1(\cdot ), \, \eta _2(\cdot ) \right) . \end{aligned}$$

(86)

It satisfies the adjoint system (54) and the maximum condition

$$\begin{aligned} u \left( {\hat{t}} \right) \,\, = \,\, {\left\{ \begin{array}{ll} u_{\min }, &{} \eta _2 \left( {\hat{t}} \right) \, < \, 0, \\ u_{\max }, &{} \eta _2 \left( {\hat{t}} \right) \, > \, 0, \end{array}\right. } \end{aligned}$$

(87)

for the Hamiltonian

$$\begin{aligned} H_1 \left( {\hat{p}}, {\hat{r}}, u, \eta _0, \eta _1, \eta _2 \right) \,\,= & {} \,\, \left( E_M \, \left( 1 - {\hat{r}} \right) \, - \, \left( 1 + {\hat{p}} \right) \, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \, - \, k_1 \, \frac{{\hat{p}} \, \left( 1 - {\hat{r}} \right) }{K_1 + {\hat{p}}} \right) \, \eta _1 \,\,\nonumber \\&+ \,\, \left( u - {\hat{r}} \right) \, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \, \eta _2 \,\, - \,\, \frac{{\hat{p}} \, {\hat{r}}}{K + {\hat{p}}} \, \eta _0. \end{aligned}$$

(88)

Let the process (86) contain a chattering arc that enters the singular regime at the optimal steady state $\left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right)$. Following Yegorov et al. (2018), we exclude abnormal extremal processes (with $\eta _0 \equiv 0$) from consideration, since they do not allow for singular regimes (due to Theorem 4.8) and therefore do not admit a clear biological interpretation. Then $\eta _0 \equiv -1$, and the conserved Hamiltonian value for the process (86) equals

$$\begin{aligned} H_1 \left| _{\small {(88)}, \,\, \left( {\hat{p}}, {\hat{r}} \right) \, = \, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right) , \,\, \eta _2 \, = \, 0, \,\, \eta _0 \, = \, -1} \right. \,\, = \,\, \frac{{\hat{p}}^*_{\mathrm {opt}} \, {\hat{r}}^*_{\mathrm {opt}}}{K + {\hat{p}}^*_{\mathrm {opt}}}. \end{aligned}$$

Let ${\hat{t}} = {\hat{t}}_{\mathrm {sw}}$ be one of bang-bang switching instants for a chattering arc of (86). If $\, d {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) /d {\hat{t}} \,= \, 0, \,$ then $\, {\hat{r}} \left( {\hat{t}}_{\mathrm {sw}} \right) \, = \, {\hat{r}}^* \left( {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) \right) \,$ (the function $\,{\hat{r}}^* = {\hat{r}}^* \left( {\hat{p}} \right) \,$ is defined by (34)) and, from the Hamiltonian conservation property, one obtains

$$\begin{aligned} \frac{{\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) \, {\hat{r}}^* \left( {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) \right) }{K + {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) } \,\, = \,\, \frac{{\hat{p}}^*_{\mathrm {opt}} \, {\hat{r}}^*_{\mathrm {opt}}}{K + {\hat{p}}^*_{\mathrm {opt}}} \,\, = \,\, \frac{{\hat{p}}^*_{\mathrm {opt}} \, {\hat{r}}^* \left( {\hat{p}}^*_{\mathrm {opt}} \right) }{K + {\hat{p}}^*_{\mathrm {opt}}}, \end{aligned}$$

which implies $\, \left( {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) , \, {\hat{r}} \left( {\hat{t}}_{\mathrm {sw}} \right) \right) \, = \, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right) \,$ due to Property 4.1 and Theorem 4.3, i.e., this is already a singular arc at ${\hat{t}} = {\hat{t}}_{\mathrm {sw}}$. Therefore, the case $\, d {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) / d {\hat{t}} \, = \, 0$ can be excluded from the consideration of chattering arcs. Then the switching condition $\, \eta _2 \left( {\hat{t}}_{\mathrm {sw}} \right) \, = \, 0 \,$ and Hamiltonian conservation property yield a correct representation (without division by zero) for the first adjoint component at ${\hat{t}} = {\hat{t}}_{\mathrm {sw}}$:

$$\begin{aligned} \begin{aligned} \eta _1 \left( {\hat{t}}_{\mathrm {sw}} \right) \,\,&= \,\, \left( E_M \, \left( 1 - {\hat{r}} \left( {\hat{t}}_{\mathrm {sw}} \right) \right) \,\, - \,\, \left( 1 + {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) \right) \, \frac{{\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) \, {\hat{r}} \left( {\hat{t}}_{\mathrm {sw}} \right) }{K + {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) } \,\, \right. \\&\quad \,\, \left. - \,\, k_1 \, \frac{{\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) \, \left( 1 - {\hat{r}} \left( {\hat{t}}_{\mathrm {sw}} \right) \right) }{K_1 + {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) } \right) ^{-1}\cdot \,\, \left( \frac{{\hat{p}}^*_{\mathrm {opt}} \, {\hat{r}}^*_{\mathrm {opt}}}{K + {\hat{p}}^*_{\mathrm {opt}}} \, - \, \frac{{\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) \, {\hat{r}} \left( {\hat{t}}_{\mathrm {sw}} \right) }{K + {\hat{p}} \left( {\hat{t}}_{\mathrm {sw}} \right) } \right) . \end{aligned} \end{aligned}$$

(89)

The formula (89) can be used for approximate setting of the values of $\eta _1$ at the points

$$\begin{aligned} \left( {\hat{p}}, {\hat{r}} \right) \,\, \in \,\, {\mathop {L}\limits ^{\circ }}_{\delta } \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\, L_{\delta } {\setminus } \left\{ \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right) \right\} \end{aligned}$$

(as was mentioned above, $\Sigma$ is close to $L_{\delta }$ in the ball (84)). Denote the corresponding representation by $\, \eta _{1, \delta } \, = \, \eta _{1, \delta } \left( {\hat{p}}, {\hat{r}} \right)$. For computational purposes, it is reasonable to discretize ${\mathop {L}\limits ^{\circ }}_{\delta }$ by the grid consisting of the points

$$\begin{aligned} Q_i \,\, {\mathop {=}\limits ^{\mathrm {def}}} \,\, \left( {\hat{p}}^*_{\mathrm {opt}}, \, {\hat{r}}^*_{\mathrm {opt}} \, + \, i \, \frac{\delta }{n} \right) , \quad i \, \in \, {\mathcal {I}}_n \, {\mathop {=}\limits ^{\mathrm {def}}} \, \{ -n, \, -n + 1, \, \ldots , \, n - 1, \, n \} {\setminus } \{ 0 \}, \end{aligned}$$

for a sufficiently large $n \in {\mathbb {N}}$. Let us rewrite the state and adjoint equations under the condition (87) in reverse time. The numerical integration of the four resulting reverse-time equations from the starting positions

$$\begin{aligned} \eta _1 \, = \, \eta _{1, \delta } \left( {\hat{p}}, {\hat{r}} \right) , \quad \eta _2 \, = \, 0, \quad \left( {\hat{p}}, {\hat{r}} \right) \, \in \, \{ Q_i \}_{i \in {\mathcal {I}}_n} \end{aligned}$$

allows to find the bang-bang switching points in the state space (at the time instants when $\eta _2$ changes its sign) and thereby to approximate $\Sigma _0$ and $\Sigma _1$. It remains to recall that $\, \Sigma \, = \, \Sigma _0 \, \cup \, \left( {\hat{p}}^*_{\mathrm {opt}}, {\hat{r}}^*_{\mathrm {opt}} \right) \, \cup \, \Sigma _1$.

Fig. 15

The optimal feedback control law in the biomass maximization problem for Model 1 under the terminal constraint (55). The parameter values are given by (48)–(51)

Note that this method of approximating $\Sigma$ in principle does not depend on a particular finite time horizon ${\hat{T}}$, although some upper time bound for integrating the reverse-time system of the state and adjoint equations has to be selected.

Figure 15 shows the switching curve $\Sigma$ approximated via the described algorithm. The global optimal feedback control law in the studied biomass maximization problem is in fact illustrated (the feedback representation combines all possible initial states together, as opposed to the time-dependent open-loop form). The corresponding parameter values (48)–(51) are the same as in Sects. 4.1.2 and 4.1.3.

Fig. 16

The chattering switching curves $\Sigma$ and $\Sigma _{k_1 \, = \, 0}$ in the biomass maximization problem for Model 1 under the terminal constraint (55), and in the biomass maximization problem of Giordano et al. (2016). Different control constraints are considered, and the other parameter values are given by (49)–(51)

Figure 16 compares $\Sigma$ with the switching curve $\Sigma _{k_1 \, = \, 0}$ for the biomass maximization problem of Giordano et al. (2016) (whose dynamical system can be obtained from the first two equations of (21) by taking $k_1 = 0$ and $u \equiv \alpha$). The parameters (49)–(51) are still the same, while different control constraints are now considered. For $\Sigma$, the control bounds $u_{\min } = 0.01$ and $u_{\max } = 0.81$ correspond to the case $\, I_{\min } = \alpha _{\min } = 0.1$, $\, I_{\max } = \alpha _{\max } = 0.9$. For $\Sigma _{k_1 \, = \, 0}$, we have $u \equiv \alpha$ and, hence, $\, u_{\min } = \alpha _{\min }$, $u_{\max } = \alpha _{\max } \,$ (here we set $I \equiv 1$ for the model of Giordano et al. (2016), because it does not contain an inducer). Moreover, $\, \left( {\hat{p}}^*_{\mathrm {opt}, \, k_1 \, = \, 0}, \, {\hat{r}}^*_{\mathrm {opt}, \, k_1 \, = \, 0} \right) \,$ denotes the optimal steady state for the problem of Giordano et al. (2016).