Integrodifference equations in the presence of climate change: persistence criterion, travelling waves and inside dynamics

Abstract

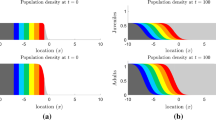
To understand the effects that the climate change has on the evolution of species as well as the genetic consequences, we analyze an integrodifference equation (IDE) models for a reproducing and dispersing population in a spatio-temporal heterogeneous environment described by a shifting climate envelope. Our analysis on the IDE focuses on the persistence criterion, travelling wave solutions, and the inside dynamics. First, the persistence criterion, characterizing the global dynamics of the IDE, is established in terms of the basic reproduction number. In the case of persistence, a unique travelling wave is found to govern the global dynamics. The effects of the size and the shifting speed of the climate envelope on the basic reproduction number, and hence, on the persistence criterion, are also investigated. In particular, the critical domain size and the critical shifting speed are found in certain cases. Numerical simulations are performed to complement the theoretical results. In the case of persistence, we separate the travelling wave and general solutions into spatially distinct neutral fractions to study the inside dynamics. It is shown that each neutral genetic fraction rearranges itself spatially so as to asymptotically achieve the profile of the travelling wave. To measure the genetic diversity of the population density we calculate the Shannon diversity index and related indices, and use these to illustrate how diversity changes with underlying parameters.

Appendices

Appendix A: Proof of Theorem 2.3

This section is devoted to the Proof of Theorem 2.3. We first present some preparatory results.

The following lemma is an immediate consequence of the stationary solution equation.

Lemma A.1

Let w be a stationary solution of (2.2). Then $w\in C_{+}(I)$. If, in addition, $w\not \equiv 0$, then $w\in C_{++}(I)$.

The next result gives the nonlinear comparison principle.

Lemma A.2

Let $\overline{w},\underline{w}\in C_{+}(I)$ satisfy $\overline{w}\ge \mathcal {F}[\overline{w}]$ and $\underline{w}\le \mathcal {F}[\underline{w}]$, respectively. If $\overline{w}\not \equiv 0$, then $\overline{w}\ge \underline{w}$.

Proof

Clearly, the conditions on $\overline{w}$ imply that $\overline{w}\in C_{++}(I)$. We assume that $\underline{w}\not \equiv 0$, otherwise there is nothing to prove. Define

$$\begin{aligned} \alpha _{*}:=\inf \left\{ \alpha >0:\alpha \overline{w}\ge \underline{w}\right\} . \end{aligned}$$

By the continuity of $\overline{w}$ and $\underline{w}$, $\alpha _{*}\overline{w}\ge \underline{w}$. Moreover, there exists $x_{0}\in I$ such that $\alpha _{*}\overline{w}(x_{0})=\underline{w}(x_{0})$.

We show $\alpha _{*}\le 1$ which leads to the result of the lemma. Suppose $\alpha _{*}>1$ for contradiction. Clearly,

$$\begin{aligned} 0\ge \int _{I}K(x_{0}-y+c)g(y)\left[ \alpha _{*}f(\overline{w}(y))-f(\underline{w}(y))\right] dy. \end{aligned}$$

As there holds

$$\begin{aligned} \alpha _{*}f(\overline{w}(y))= & {} \alpha _{*}\overline{w}(y)\frac{f(\overline{w}(y))}{\overline{w}(y)}>\alpha _{*}\overline{w}(y)\frac{f(\alpha _{*}\overline{w}(y))}{\alpha _{*}\overline{w}(y)}\\= & {} f(\alpha _{*}\overline{w}(y))>f(\underline{w}(y)),\quad \forall y\in I, \end{aligned}$$

where we used (H)-(2), we find

$$\begin{aligned} \int _{I}K(x_{0}-y+c)g(y)\left[ \alpha _{*}f(\overline{w}(y))-f(\underline{w}(y))\right] dy>0, \end{aligned}$$

which leads to a contradiction.$\square$

The above lemma leads immediately to the uniqueness of non-zero stationary solution of (2.2).

Corollary A.3

There exists at most one non-zero stationary solution of (2.2).

The following comparison principle for sub- and super-solutions of (2.2) is trivial.

Lemma A.4

Let $\{\overline{w}_{n}\}_{n}\subset C_{+}(I)$ and $\{\underline{w}_{n}\}_{n}\subset C_{+}(I)$ satisfy $\overline{w}_{n+1}\ge \mathcal {F}[\overline{w}_{n}]$ and $\underline{w}_{n+1}\le \mathcal {F}[\underline{w}_{n}]$, respectively. If $\overline{w}_{0}\ge \underline{w}_{0}$, then $\overline{w}_{n}\ge \underline{w}_{n}$ for all n.

Now, we are ready to prove Theorem 2.3. We first prove Theorem 2.3(1).

Proof (Proof of Theorem 2.3(1))

Suppose $R_{0}\le 1$ first. Clearly, 0 is a stationary solution of (2.2). It remains to show that positive stationary solutions do not exist in this case. For contradiction, let us suppose the existence of a positive stationary solution w of (2.2). By Lemma A.1, $\min _{I}w>0$. By (H)-(2),

$$\begin{aligned} f(w(y))=w(y)\frac{f(w(y))}{w(y)}<r_{0}w(y),\quad y\in I, \end{aligned}$$

which implies that $w(x)<\mathcal {F}_{0}[w](x)$ for all $x\in I$. Therefore, we can find some $\delta \in (0,1)$ such that $w\le (1-\delta )\mathcal {F}_{0}[w]$. We then iterate to obtain

$$\begin{aligned} w\le (1-\delta )^{n}\mathcal {F}_{0}^{n}[w],\quad \forall n\in \mathbb {N}. \end{aligned}$$

Recall that $\phi _{0}\in C_{++}(I)$ is the eigenfunction associated to $R_{0}$. We may assume, without loss of generality, that $w\le \phi _{0}$. It then follows that $\mathcal {F}_{0}^{n}[w]\le \mathcal {F}_{0}^{n}[\phi _{0}]=R_{0}^{n}\phi _{0}\le \phi _{0}$, which leads to

$$\begin{aligned} w\le (1-\delta )^{n}\phi _{0},\quad \forall n\in \mathbb {N}. \end{aligned}$$

This yields $w\equiv 0$. It is a contradiction.

Now, suppose $R_{0}>1$. By Lemma A.1 and Corollary A.3, it suffices to find one positive stationary solution of (2.2). To do so, let us consider for $\epsilon >0$ the sequence $\{w_{n}^{\epsilon }\}_{n}$ defined by

$$\begin{aligned} w_{0}^{\epsilon }=\epsilon \phi _{0}\quad \text {and}\quad w_{n+1}^{\epsilon }=\mathcal {F}[w_{n}^{\epsilon }],\,\,n\in \mathbb {N}_{0}. \end{aligned}$$

Let $\delta _{0}>0$ be such that $\frac{R_{0}}{1+\delta _{0}}>1$. It is clear that $R_{0}=r(\mathcal {F}_{0})\le \Vert \mathcal {F}_{0}\Vert \le r_{0}=f'(0)$. Since the limit $\lim _{\epsilon \rightarrow 0^{+}}\frac{f(\epsilon \phi _{0}(x))}{\epsilon \phi _{0}(x)}=f'(0)$ is uniform in $x\in I$, we can find some $\epsilon _{0}>0$ such that $\frac{f(\epsilon _{0}\phi _{0})}{\epsilon _{0}\phi _{0}}\ge \frac{R_{0}}{1+\delta _{0}}$. It then follows the assumption on f that $\frac{f(\epsilon \phi _{0})}{\epsilon \phi _{0}}\ge \frac{R_{0}}{1+\delta _{0}}$ for all $\epsilon \in (0,\epsilon _{0}]$. We see that

$$\begin{aligned} w_{1}^{\epsilon }=\int _{I}K(\cdot -y+c)g(y)\epsilon \phi _{0}\frac{f(\epsilon \phi _{0})}{\epsilon \phi _{0}}dy\ge {\frac{R_{0}}{1+\delta _{0}}\mathcal {F}_{0}[\epsilon \phi _{0}]}=\frac{R_{0}}{1+\delta _{0}}\epsilon \phi _{0}>\epsilon \phi _{0} \end{aligned}$$

for all $\epsilon \in (0,\epsilon _{0}]$. It then follows from Lemma A.4 that $w_{n+1}^{\epsilon }\ge w_{n}^{\epsilon }$ for all $\epsilon \in (0,\epsilon _{0}]$.

Let us fix any $\epsilon \in (0,\epsilon _{0}]$. By the boundedness of f, it is clear that $\{w_{n}^{\epsilon }\}$ is uniformly bounded, and hence, the limit function $w_{*}:=\lim _{n\rightarrow \infty }w_{n}^{\epsilon }$ is well-defined. It is easy to see that $w_{*}$ is a positive stationary solution of (2.2). The upper bound on $w_{*}$ as in the statement is trivial. This completes the proof.$\square$

We denote by $w_{*}$ the unique positive stationary solution of (2.2) when $R_{0}>1$. In the Proof of Theorem 2.3(1), we have proven the following result.

Corollary A.5

There exists $\epsilon _{0}>0$ such that for any $\epsilon \in (0,\epsilon _{0}]$, the sequence $\{\mathcal {F}^{n}[\epsilon \phi _{0}]\}_{n}$ is increasing and converges in C(I) to $w_{*}$ as $n\rightarrow \infty$.

Proof

We only need to point out that the convergence in C(I) comes from Dini’s theorem.$\square$

Finally, we prove Theorem 2.3(2).

Proof (Proof of Theorem 2.3(2))

For $M\ge \sup _{u\in [0,\infty )}f(u)$, we have $\mathcal {F}[M]<M$. It follows that $\{\mathcal {F}^{n}[M]\}_{n}$ is a decreasing sequence. By Theorem 2.3 and Dini’s theorem,

$$\begin{aligned} \mathcal {F}^{n}[M]\rightarrow {\left\{ \begin{array}{ll} 0,&{}\,\,\text {if}\,\,R_{0}\le 1,\\ w_{*}&{}\,\,\text {if}\,\,R_{0}>1 \end{array}\right. } \quad \text {in}\,\,C(I)\,\,\text {as}\,\,n\rightarrow \infty . \end{aligned}$$

This together with Lemma A.4 yield the result in the case $R_{0}\le 1$. In the case of $R_{0}>1$, we can find some $\epsilon _{0}>0$ and $M_{0}>0$ such that $\epsilon _{0}\phi _{0}\le w_{1}\le M_{0}$. We then conclude the result from Lemma A.4 and Corollary A.5.$\square$

Fig. 7

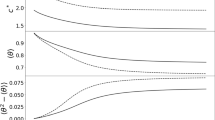
A heat map for the $\text {Div}^q$ diversity index of (3.12) where a $q=0.2$, b $q=1$, c $q=2$, and d $q=\infty$. In these simulations we use the following parameter values, $R=1.5$, $K_{*}=1$, $\sigma ^2 = 0.02$ and $\mu =0$

Fig. 8

A heat map for the $\text {Div}^q$ diversity index of (3.12) where a $q=0.2$, b $q=1$, c $q=2$, and d $q=\infty$. In these simulations we use the following parameter values, $R=1.5$, $K_{*}=1$, $\sigma ^2 = 0.02$ and $\mu =0.2$

Appendix B: Comparison of Fig. 5 with other diversity indices

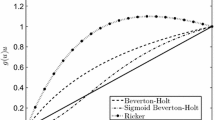
To make a complete analysis of the patterns seen in Fig. 5 we provide similar plots for different diversity measures. We consider the diversity index

$$\begin{aligned} \text {Div}^q = \left( \sum _{i=1}^N (p^i)^q\right) ^{\frac{1}{1-q}}. \end{aligned}$$

(B.1)

for $0< q <1$ and $1<q < \infty$. In the limit as $q \rightarrow 1$, it can be shown that

$$\begin{aligned} \text {Div}^1 = \text {exp}\left( -\sum _{i=1}^N p^i \ln (p^i) \right) , \end{aligned}$$

(B.2)

yielding that $\text {Div}^1$ is the exponential of the Shannon diversity index. When $q=0$ the diversity index becomes the species richness and when $q=\infty$ the diversity index becomes a measure of species evenness, given by the maximum $p^i$ value. In Figs. 7 and 8 we provide plots constructed in the same manner as Fig. 5.