Abstract
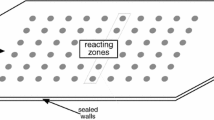
Optical biosensors are devices used to investigate surface-volume reaction kinetics. Current mathematical models for reaction dynamics rely on the assumption of unidirectional flow within these devices. However, new devices, such as the Flexchip, include a geometry that introduces two-dimensional flow, complicating the depletion of the volume reactant. To account for this, a previous mathematical model is extended to include two-dimensional flow, and the Schwarz–Christoffel mapping is used to relate the physical device geometry to that for a device with unidirectional flow. Mappings for several Flexchip dimensions are considered, and the ligand depletion effect is investigated for one of these mappings. Estimated rate constants are produced for simulated data to quantify the inclusion of two-dimensional flow in the mathematical model.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Carrier GF, Krook M, Pearson CE (2005) Functions of a complex variable: theory and technique (classics in applied mathematics). Society for Industrial and Applied Mathematics, Philadelphia
Driscoll T, Trefethen L (2005) Schwarz–Christoffel mapping (Cambridge monographs on applied and computational mathematics). Cambridge University Press, Cambridge
Driscoll TA (2013) The Schwarz–Christoffel toolbox for MATLAB. http://www.math.udel.edu/~driscoll/SC
Edwards DA (1999) Estimating rate constants in a convection-diffusion system with a boundary reaction. IMA J Appl Math 63:89–112
Edwards DA (2001) The effect of a receptor layer on the measurement of rate constants. Bull Math Bio 63:301–327
Edwards DA (2011) Transport effects on surface reaction arrays: biosensor applications. Math Biosci 230:12–22
GE Healthcare (2006) Biacore Flexchip product information. Uppsala
GE Healthcare (2007) Label-free interaction analysis in real-time using surface plasmon resonance, (technology note 23)
Mason T, Pineda AR, Wofsy C, Goldstein B (1999) Effective rate models for the analysis of transport-dependent biosensor data. Math Biosci 159:123–144
Rich RL, Cannon MJ, Jenkins J, Pandian P, Sundaram S, Magyar R, Brockman J, Lambert J, Myszka DG (2008) Extracting kinetic rate constants from surface plasmon resonance array systems. Anal Biochem 373(1):112–120
Zumbrum M (2014) The effect of receptor nonuniformity for surface reactions within optical biosensors. IMA J Appl Math (submitted)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zumbrum, M.E., Edwards, D.A. Conformal mapping in optical biosensor applications. J. Math. Biol. 71, 533–550 (2015). https://doi.org/10.1007/s00285-014-0827-2
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-014-0827-2