Abstract
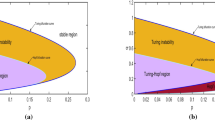
By introducing linear cross-diffusion for a two-component reaction-diffusion system with activator-depleted reaction kinetics (Gierer and Meinhardt, Kybernetik 12:30–39, 1972; Prigogine and Lefever, J Chem Phys 48:1695–1700, 1968; Schnakenberg, J Theor Biol 81:389–400, 1979), we derive cross-diffusion-driven instability conditions and show that they are a generalisation of the classical diffusion-driven instability conditions in the absence of cross-diffusion. Our most revealing result is that, in contrast to the classical reaction-diffusion systems without cross-diffusion, it is no longer necessary to enforce that one of the species diffuse much faster than the other. Furthermore, it is no longer necessary to have an activator–inhibitor mechanism as premises for pattern formation, activator–activator, inhibitor–inhibitor reaction kinetics as well as short-range inhibition and long-range activation all have the potential of giving rise to cross-diffusion-driven instability. To support our theoretical findings, we compute cross-diffusion induced parameter spaces and demonstrate similarities and differences to those obtained using standard reaction-diffusion theory. Finite element numerical simulations on planary square domains are presented to back-up theoretical predictions. For the numerical simulations presented, we choose parameter values from and outside the classical Turing diffusively-driven instability space; outside, these are chosen to belong to cross-diffusively-driven instability parameter spaces. Our numerical experiments validate our theoretical predictions that parameter spaces induced by cross-diffusion in both the \(u\) and \(v\) components of the reaction-diffusion system are substantially larger and different from those without cross-diffusion. Furthermore, the parameter spaces without cross-diffusion are sub-spaces of the cross-diffusion induced parameter spaces. Our results allow experimentalists to have a wider range of parameter spaces from which to select reaction kinetic parameter values that will give rise to spatial patterning in the presence of cross-diffusion.


















Similar content being viewed by others
References
Bard J, Lauder I (1974) How well does Turing’s Theory of morphogenesis work? J Theoret Biol 45:501–531
Barreira R, Elliott CM, Madzvamuse A (2011) The surface finite element method for pattern formation on evolving biological surfaces. J Math Biol 63:1095–1119
Capasso V, Liddo D (1994) Asymptotic behaviour of reaction-diffusion systems in population and epidemic models. The role of cross-diffusion. J Math Biol 32:453–463
Capasso V, Liddo D (1993) Global attractivity for reaction-diffusion systems. The case of nondiagonal diffusion matrices. J Math Anal Appl 177:510–529
Crampin EJ, Hackborn WW, Maini PK (2002) Pattern formation in reaction-diffusion models with nonuniform domain growth. Bull Math Biol 64:746–769
Dillion R, Maini PK, Othmer HG (1994) Pattern formation in generalized Turing systems. J Math Biol 32:345–393
Epstein IR, Pojman JA (1998) An introduction to nonlinear chemical dynamics (Topics in Physical Chemistry). Oxford University Press, New York
Gambino G, Lombardo MC, Sammartino M (2012) Turing instability and traveling fronts for nonlinear reaction-diffusion system with cross-diffusion. Math Comp Sim 82:1112–1132
Gambino G, Lombardo MC, Sammartino M (2013) Pattern formation driven by cross-diffusion in 2-D domain. Nonlinear Anal Real World Appl 14:1755–1779
Gierer A, Meinhardt H (1972) A theory of biological pattern formation. Kybernetik 12:30–39
Gray P, Scott SK (1990) Chemical oscillations and instabilities. Oxford University Press, New York, Nonlinear chemical kinetics
Hillen T, Painter KJ (2009) A user’s guide to PDE models for chemotaxis. J Math Biol 58:183–217
Iida M, Mimura M (2006) Diffusion, cross-diffusion an competitive interaction. J Math Biol 53:617–641
Kovács S (2004) Turing bifurcation in a system with cross-diffusion. Nonlinear Anal 59:567–581
Li L, Jin Z, Sun G (2008) Spatial pattern of an epidemic model with cross-diffusion. Chin Phys Lett 25:3500
Madzvamuse A, Gaffney EA, Maini PK (2010) Stability analysis of non-autonomous reaction-diffusion systems: the effects of growing domains. J Math Biol 61(1):133–164
Madzvamuse A, Maini PK, Wathen AJ (2003) A moving grid finite element method applied to a model biological pattern generator. J Comp Phys 190:478–500
Madzvamuse A, Thomas Roger K, Maini Philip K, Wathen Andrew J (2002) A Numerical Approach to the Study of Spatial Pattern Formation in the Ligaments of Arcoid Bivalves. Bull Math Biol 64:501–530
McAfree MS, Annunziata O (2013) Cross-diffusion in a colloid-polymer aqueous system. Fluid Phase Equilibr 356:46–55. Bull Math Biol 64:501–530
Murray JD (1982) Parameter space for Turing instabiity in reaction diffusion mechanisms: a comparison of models. J Theor Biol 98:143–163
Murray JD (2003) Mathematical Biology II: spatial models and biomedical applications, 3rd edn. Springer, Berlin
Painter KJ, Othmer HG, Maini PK (1999) Stripe formation in juvenile Pomacanthus explained by a generalized Turing mechanism with chemotaxis. Proc Natl Acad Sci 96:5549
Prigogine I, Lefever R (1968) Symmetry breaking instabilities in dissipative systems, II. J Chem Phys 48:1695–1700
Rossi F, Vanag VK, Tiezzi E, Epstein IR (2010) Quaternary cross-diffusion in water-in-oil microemulsions loaded with a component of the Belousov-Zhabotinsky reaction. J Phys Chem B 114:8140–8146
Ruiz-Baier R, Tian C (2013) Mathematical analysis and numerical simulation of pattern formation under cross-diffusion. Nonlinear Anal Real World Appl 14:601–612
Schnakenberg J (1979) Simple chemical reaction systems with limit cycle behaviour. J Theor Biol 81:389–400
Shi J, Xie Z, Little K (2011) Cross-diffusion induced instability and stability in reaction-diffusion systems. J Appl Anal Comp 1(1):95–119
Thomas D (1975) Artificial enzyme membrane, transport, memory and oscillatory phenomena. In: Thomas D, Kervenez J-P (eds) Analysis and control of immobilised enzyme systems. Springer, Heidelberg, pp 115–150
Tian Lin Z, Pedersen M (2010) Instability induced by cross-diffusion in reaction-diffusion systems. Nonlinear Anal Real World Appl 11:1036–1045
Turing A (1952) On the chemical basis of morphogenesis. Phil Trans R Soc B 237:37–72
Tyrrell HJV, Harris KR (1984) Diffusion in liquids. Butterworths, London
Vanag VK, Epstein IR (2009) Cross-diffusion and pattern formation in reaction diffusion systems. Phys Chem Chem Phys 11:897–912
Vergara A, Capuano F, Paduano L, Sartorio R (2006) Lysozyme mutual diffusion in solutions crowded by poly(ethylene glycol). Macromolecules 39:4500–4506
Xie Z (2012) Cross-diffusion induced Turing instability for a three species food chain model. J Math Anal Appl 388:539–547
Zhabotinsky AM (1991) A history of chemical oscillations and waves. Chaos 1:379–86
Zhang J-F, Li W-T, Wang Y-X (2011) Turing patterns of a strongly coupled predator-prey system with diffusion effects. Nonlinear Anal 74:847–858
Zemskov EP, Vanag VK, Epstein IR (2011) Amplitude equations for reaction-diffusion systems with cross-diffusion. Phys Rev E 84:036216
Acknowledgments
This work (AM) is supported by the following grants: EPSRC research grant (EP/J016780/1): Modeling, analysis and simulation of spatial patterning on evolving surfaces.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Madzvamuse, A., Ndakwo, H.S. & Barreira, R. Cross-diffusion-driven instability for reaction-diffusion systems: analysis and simulations. J. Math. Biol. 70, 709–743 (2015). https://doi.org/10.1007/s00285-014-0779-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-014-0779-6
Keywords
- Cross-diffusion reaction systems
- Cross-diffusion driven instability
- Parameter space identification
- Pattern formation
- Planary domains
- Finite element method