Skip to main content

Advertisement

SpringerLink
Log in

Effect of parity on productivity and sustainability of Lotka–Volterra food chains

Bounded orbits in food chains

  • Published:
Journal of Mathematical Biology Aims and scope Submit manuscript

Abstract

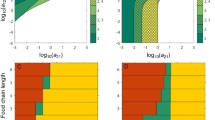
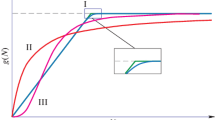
Hairston, Slobodkin, and Smith conjectured that top down forces act on food chains, which opposed the previously accepted theory that bottom up forces exclusively dictate the dynamics of populations. We model food chains using the Lotka–Volterra predation model and derive sustainability constants which determine which species will persist or go extinct. Further, we show that the productivity of a sustainable food chain with even trophic levels is predator regulated, or top down, while a sustainable food chain with odd trophic levels is resource limited, which is bottom up, which is consistent with current ecological theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  • Chauvet E, Paullet J, Previte JP, Walls Z (2002) A Lotka–Volterra three species food chain. Math Mag 75(4):243–255

    Article  MATH  MathSciNet  Google Scholar 

  • DeAngelis D (1992) Dynamics of nutrient cycling and food webs. Chapman and Hall, London

    Book  Google Scholar 

  • Fretwell SD (1977) The regulation of plant communities by the food chains exploiting them. Perpsect Biol Med 20:169–185

    Google Scholar 

  • Gard T, Hallam T (1979) Persistence in food webs-I Lotka–Volterra food chains. Bull Math Biophys 41:877–891

    MATH  MathSciNet  Google Scholar 

  • Gopalsamy K (1984) Global asymptotic stability in Volterra’s population systems. J Math Biol 19:157–168

    Article  MATH  MathSciNet  Google Scholar 

  • Hairston N, Smith F, Slobodkin L (1960) Community structure, population control, and competition. Am Nat 94(879):421–425

    Article  Google Scholar 

  • Harris S, Paullet JE, Previte JP, Ranola J (2005) A Lotka–Volterra four species food chain (unpublished)

  • Harrison GW (1979) Global stability of food chains. Am Nat 114(3):455–457

    Article  Google Scholar 

  • Heath M, Speirs D, Steele J (2013) Understanding patterns and processes in models of trophic cascades. Ecol Lett. doi:10.1111/ele.12200

  • Lotka AJ (1925) Elements of physical biology. Williams and Wilkins Co, Baltimore

    MATH  Google Scholar 

  • Odum E (1953) Fundamentals of Ecology. W. B. Saunders Company, Philadelphia

    Google Scholar 

  • Oksanen L, Fretwell S, Arruda J, Niemela P (1981) Exploitation ecosystems in gradients of primary productivity. Am Nat 118:240–261

    Article  Google Scholar 

  • Persson L, Diehl S, Johansson L, Andersson G, Hamrin SF (1992) Trophic interactions in temperate lake ecosystems: a test of food chain theory. Am Nat 140(1):59–84

    Article  Google Scholar 

  • Polis GA, Strong DR (1996) Food web complexity and community dynamics. Am Nat 147(5):813–846

    Article  Google Scholar 

  • Roy A, Solimano F (1987) Global stability and oscillations in classical Lotka–Volterra loops. J Math Biol 24:603–617

    Article  MATH  MathSciNet  Google Scholar 

  • Smith DW (2005) Ten years of yellowstone wolves, 1995–2005. Yellowstone Sci 13(1):7–31

    Google Scholar 

  • Volterra V (1931) Variations and fluctuations of the number of individuals in animal species living together. In: Chapman R (ed) Animal Ecology. McGraw-Hill, New York

    Google Scholar 

  • Wollrab S, Diehl S, Roos AD (2012) Simple rules describe bottom-up and top-down control in food webs with alternate energy pathyways. Ecol Lett 15(9):935–946

    Article  Google Scholar 

Download references

Acknowledgments

We thank the reviewers for their insightful comments and helpful suggestions. J.P.P. acknowledges support from NSF-DMS-9987594, NSF-DMS-0236637, and NSF-DMS-0552148 for foundational work that led to the formulation of this problem.

Author information

Authors and Affiliations

  1. University of Maryland Baltimore County, 1000 Hilltop Circle, Baltimore, MD,  21250, USA

    Nicole Massarelli & Kathleen Hoffman

  2. Penn State Erie, The Behrend College, Station Road, Erie, PA,  16563, USA

    Joseph P. Previte

Authors
  1. Nicole Massarelli
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kathleen Hoffman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Joseph P. Previte
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kathleen Hoffman.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Massarelli, N., Hoffman, K. & Previte, J.P. Effect of parity on productivity and sustainability of Lotka–Volterra food chains. J. Math. Biol. 69, 1609–1626 (2014). https://doi.org/10.1007/s00285-013-0746-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00285-013-0746-7

Keywords

Mathematics Subject Classification (2000)

Search

Navigation