Global asymptotic stability of plant-seed bank models

Abstract

Many plant populations have persistent seed banks, which consist of viable seeds that remain dormant in the soil for many years. Seed banks are important for plant population dynamics because they buffer against environmental perturbations and reduce the probability of extinction. Viability of the seeds in the seed bank can depend on the seed’s age, hence it is important to keep track of the age distribution of seeds in the seed bank. In this paper we construct a general density-dependent plant-seed bank model where the seed bank is age-structured. We consider density dependence in both seedling establishment and seed production, since previous work has highlighted that overcrowding can suppress both of these processes. Under certain assumptions on the density dependence, we prove that there is a globally stable equilibrium population vector which is independent of the initial state. We derive an analytical formula for the equilibrium population using methods from feedback control theory. We apply these results to a model for the plant species Cirsium palustre and its seed bank.

Appendices

Appendix A

Proof of Theorem 3.2

Without loss of generality, we can assume that $n_0$ is in $K_1 \setminus \{0\}$. If it is not, then $s_i \ne 0$ for some $i = 1, 2, \ldots N$, which would imply that $n_1 \in K_1 \setminus \{0\}.$

To prove part (1) of Theorem 3.2, since $(\tilde{c}_{1}^T(\tilde{I}-\tilde{A}_{1})^{-1}\tilde{b})^{-1} > g_0 = \sup _{y>0} g(y)$ and $h(y) \le y$,

$$\begin{aligned} \tilde{n}_{t+1} \le \tilde{A_{1}}\tilde{n}_t + \tilde{b}g(\tilde{c}_1^T\tilde{n}_t)\tilde{c}_1^T\tilde{n}_t\le \tilde{A}_{1}\tilde{n}_t + m\tilde{b}\tilde{c}_{1}^T\tilde{n}_t, \end{aligned}$$

for some $m < p_1$. By induction

$$\begin{aligned} \tilde{n}_t \le (\tilde{A}_1 + m\tilde{b}\tilde{c}_1^T)^t\tilde{n}_0, \qquad t \in \mathbb N . \end{aligned}$$

Since $p_1 = (\tilde{c}_{1}^T(\tilde{I}-\tilde{A}_{1})^{-1}\tilde{b})^{-1}$ is the stability radius of $(\tilde{A}_{1}, \tilde{b}, \tilde{c}_{1}^T)$, we have that $r(\tilde{A}_{1} + m\tilde{b}\tilde{c}_{1}^T)<1$. Thus

$$\begin{aligned} \lim _{t \rightarrow \infty }\tilde{n}_{t}=0. \end{aligned}$$

The $(\epsilon , \delta )$ conclusion follows from the boundedness of $\tilde{A}_{1} + m\tilde{b}\tilde{c}_{1}^T$.

For (2), with the triple $(p_1, p_2, y^*) \in (0,g_0)\times (0,1)\times (0,\infty )$ satisfying (3.10) define the functional

$$\begin{aligned} \tilde{w}_{p_2}^T:=\tilde{c}_{p_2}^T(\tilde{I} - \tilde{A}_{p_2})^{-1}. \end{aligned}$$

(6.1)

It is straightforward to verify that

$$\begin{aligned} \tilde{w}_{p_2}^T(\tilde{A}_{p_2} +p_1\tilde{b}\tilde{c}_{p_2}^T)=\tilde{w}_{p_2}^T. \end{aligned}$$

(6.2)

Applying $\tilde{w}_{p_2}^T$ to (2.7),

$$\begin{aligned} \tilde{w}_{p_2}^T\tilde{n}_{t+1}=\tilde{w}_{p_2}^T\tilde{A}\tilde{n}_t + \tilde{w}_{p_2}^T\tilde{b}f(\tilde{y}_t). \end{aligned}$$

(6.3)

If $\tilde{y}_t \le y^*$ and $c^Tn_t \le c^Tn^*$, then, since both $f$ and $h$ are increasing, concave down with $f(0) = h(0) = 0$, we have that $f(\tilde{y}_t) \ge p_1y_t$ and $h(c^Tn_t) \ge p_2c^Tn_t$, so (6.3) implies that

$$\begin{aligned} \tilde{w}_{p_2}^T\tilde{n}_{t+1}\ge \tilde{w}_{p_2}^T(\tilde{A}_{p_2} + p_1\tilde{b}\tilde{c}_{p_2}^T)\tilde{n}_t =\tilde{w}_{p_2}^T\tilde{n}_t. \end{aligned}$$

(6.4)

If $\tilde{y}_t \le y^*$ and $c^Tn_t \ge c^Tn^*$, then $f(\tilde{y}_t) \ge p_1\tilde{y}_t$ and $h(c^Tn_t) \ge p_2c^Tn^*$, so (6.3) implies that

$$\begin{aligned} \tilde{w}_{p_2}^T\tilde{n}_{t+1}\ge \tilde{w}_{p_2}^T\tilde{A}\tilde{n}_t + \tilde{w}_{p_2}^Tp_1\tilde{b}(\alpha _1h(c^Tn_t) + \alpha ^Ts_t) \ge p_2p_1\alpha _1\tilde{w}_{p_2}^T\tilde{b}c^Tn^*. \end{aligned}$$

(6.5)

If $\tilde{y}_t \ge y^*$, then $f(\tilde{y}_t) \ge p_1y^*$, so (6.3) implies that

$$\begin{aligned} \tilde{w}_{p_2}^T\tilde{n}_{t+1}\ge \tilde{w}_{p_2}^T\tilde{A}\tilde{n}_t + \tilde{w}_{p_2}^Tp_1\tilde{b}y^*\ge p_1\tilde{w}_{p_2}^T\tilde{b}y^*. \end{aligned}$$

(6.6)

Hence (6.4), (6.5) and (6.6) imply that

$$\begin{aligned} \tilde{w}_{p_2}^T \tilde{n}_t\ge \mathrm min \{\tilde{w}_{p_2}^T\tilde{n}_0,\; p_2p_1\alpha _1\tilde{w}_{p_2}^T\tilde{b}c^Tn^*,\; p_1\tilde{w}_{p_2}^T\tilde{b}y^*\}. \end{aligned}$$

(6.7)

By Holder’s inequality

$$\begin{aligned} \tilde{w}_{p_2}^T\tilde{n}_t \le \Vert \tilde{w}_{p_2}\Vert \Vert \tilde{n}_t\Vert , \quad \mathrm{so} \quad \Vert \tilde{n}_t\Vert \ge \frac{1}{\Vert \tilde{w}_{p_2}\Vert }\tilde{w}_{p_2}^T\tilde{n}_t. \end{aligned}$$

(6.8)

Using again that either $h(c^Tn_t) \ge p_2c^Tn_t$ or $h(c^Tn_t) \ge p_2c^Tn^* = \frac{p_1p_2y^*}{p_e}$, it follows from (6.8) that

$$\begin{aligned} \tilde{y}_t = \alpha _1h(c^Tn_t) + \alpha ^Ts_t \ge \min \{\frac{\min \{\alpha _1 p_2c_{\min },\alpha _{\min }\}}{||\tilde{w}_{p_2}^T||}\tilde{w}_{p_2}^T\tilde{n}_t, \; \frac{\alpha _1p_1p_2y^*}{p_e}\}. \end{aligned}$$

Finally, since $\tilde{n}_0$ is a positive vector in $X_1\otimes X_2$,

$$\begin{aligned} (\tilde{I} - \tilde{A}_{p_2})^{-1}\tilde{n}_0 = \tilde{n}_0 +\sum _{j=1}^\infty \tilde{A}_{p_2}^k\tilde{n}_0\ge \tilde{n}_0. \end{aligned}$$

(6.9)

Thus,

$$\begin{aligned} \tilde{w}_{p_2}^T\tilde{n}_0 = \tilde{c}_{p_2}^T(\tilde{I} - \tilde{A}_{p_2})^{-1}\tilde{n}_0 > \min \{\alpha _1p_2c_{\min },\alpha _{\min }\}\Vert \tilde{n}_0\Vert \end{aligned}$$

(6.10)

Similarly, $p_2p_1\alpha _1\tilde{w}_{p_2}^T\tilde{b}c^Tn^*$, and $\tilde{w}_{p_2}^T\tilde{b}p_1y^*$ are positive, so $\tilde{y}_t$ is bounded away from zero for all $t>0$. Also, using condition (E3) and the fact that $n_0 \in K_1 \setminus \{0\}$, $c^Tn_t$ is bounded away from zero for all $t>0$, by a similar argument. Thus, since $f$ and $h$ are increasing and concave down (see Fig. 6), from the secant slopes

$$\begin{aligned} \frac{|f(\tilde{y}_t) - f(y^*)|}{|\tilde{y}_t - y^*|}<p_1 \quad \frac{|h(c^Tn_t) - h(c^Tn^*)|}{|c^Tn_t - c^Tn^*|}<p_2, \end{aligned}$$

(6.11)

we can find $m_1 < p_1$ and $m_2 < p_2$ such that for all $t \ge 0$,

$$\begin{aligned} |f(\tilde{y}_t) - f(y^*)|\le m_1|\tilde{y}_t - y^*| \quad |h(c^Tn_t) - h(c^Tn^*)| \le m_2|c^Tn_t - c^Tn^*|.\nonumber \\ \end{aligned}$$

(6.12)

We can easily verify from (3.8) that $\tilde{n}^* = \tilde{A}_{p_2}\tilde{n}^* + p_1\tilde{b}\tilde{c}_{p_2}^T\tilde{n}^*=\tilde{A}\tilde{n}^* + \tilde{b}f(y^*)$ by construction. Thus

$$\begin{aligned} \tilde{n}_{t+1} - \tilde{n}^* = \tilde{A}\tilde{n}_t - \tilde{A}\tilde{n}^* + \tilde{b}f(\tilde{y}_t) - \tilde{b}f(y^*). \end{aligned}$$

(6.13)

Since $\tilde{A}$ is nonlinear, the variation of parameters formula becomes

$$\begin{aligned} \tilde{n}_t - \tilde{n}^*&= \tilde{A}(\tilde{A}(\cdots \tilde{A}(\tilde{A}\tilde{n_0} + \tilde{b}f(\tilde{y_0})) + bf(\tilde{y}_1)) + \cdots ) \nonumber \\&\quad + \tilde{b}f(\tilde{y}_{t-2})) + \tilde{b}f(\tilde{y}_{t-1}) - \tilde{A}\tilde{n}^* - \tilde{b}f(y^*) \end{aligned}$$

(6.14)

Since the $X_1 \rightarrow X_1$ and $X_2 \rightarrow X_1$ components of $\tilde{A}$ ($[A \; \; \emptyset ]$) are linear, and $\tilde{b} = [b \; \; 0]^T$ we have that the $X_1$ component of $\tilde{n}_t - \tilde{n}^*$ satisfies

$$\begin{aligned} n_{t} - n^*= A^t(n_0- n^*) + \sum _{j=0}^{t-1}A^{t - j -1}b(f(\tilde{y}_j) - f(y^*)). \end{aligned}$$

(6.15)

Multiplying (6.15) on the left by $\tilde{c}_{p_2}^T$, we have

$$\begin{aligned} \alpha _1p_2c^T(n_t - n^*)&= \alpha _1p_2c^TA^t(n_0-n^*) \nonumber \\&\quad + \alpha _1p_2\sum _{j=0}^{t-1}c^TA^{t-j-1}b(f(\tilde{y}_j) - f(y^*)), \end{aligned}$$

(6.16)

Taking absolute values and using positivity gives us that

$$\begin{aligned} |\alpha _1p_2c^T(n_t - n^*)|&\le \alpha _1 p_2 | c^T A^t(n_0-n^*)| \nonumber \\&\quad + \alpha _1p_2\sum _{j=0}^{t-1}c^TA^{t-j-1}b|f(\tilde{y}_j) - f(y^*)|. \end{aligned}$$

(6.17)

Using (6.12),

$$\begin{aligned} |\alpha _1p_2c^T(n_t - n^*)|&\le \alpha _1p_2|c^TA^t(n_0-n^*)| + \alpha _1p_2m_1\sum _{j=0}^{t-1}c^TA^{t-j-1}b(\alpha _1|h(c^Tn_j) \\&\quad -h(c^Tn^*)| + |\alpha ^T(s_j - s^*)|)\\&\le \alpha _1 p_2|c^TA^t(n_0-n^*)| + \alpha _1p_2m_1\sum _{j=0}^{t-1}c^TA^{t-j-1}b \\&\quad \times (\alpha _1m_2|c^Tn_j -c^Tn^*| + |\alpha ^T(s_j - s^*)|). \end{aligned}$$

Summing from $t = 0$ to $M$, where $M$ is large, we have

$$\begin{aligned} \sum _{t=0}^M |\alpha _1p_2c^T(n_t - n^*)|&\le \sum _{t=0}^M\alpha _1p_2|c^TA^t(n_0-n^*)| \nonumber \\&\quad +\alpha _1p_2m_1\sum _{t=0}^M \sum _{j=0}^{t-1}c^TA^{t-j-1}b \nonumber \\&\quad \times \left( \alpha _1m_2|c^Tn_j -c^Tn^*| + |\alpha ^T(s_j - s^*)|\right) .\quad \quad \end{aligned}$$

(6.18)

Since $r(A) < 1$ the first term in (6.18) converges as $M \rightarrow \infty$. If we rearrange the second sum and use the fact that the system is positive, we have

$$\begin{aligned} \sum _{t=0}^M|\alpha _1p_2c^T(n_t - n^*)|&\le \sum _{t=0}^{\infty }\alpha _1p_2|c^TA^t(n_0-n^*)|\\&\quad + \alpha _1p_2m_1\sum _{j=0}^{M-1}(\alpha _1m_2|c^Tn_j -c^Tn^*| + |\alpha ^T(s_j - s^*)|)\\&\quad \times \sum _{t=j + 1}^M c^TA^{t-j-1}b. \end{aligned}$$

Adding more terms and changing indices

$$\begin{aligned} \sum _{t=0}^M|\alpha _1p_2c^T(n_t - n^*)|&\le \sum _{t=0}^{\infty }\alpha _1 p_2|c^TA^t(n_0-n^*)| \nonumber \\&+ \alpha _1p_2m_1\sum _{t=0}^{M-1}(\alpha _1m_2|c^Tn_t -c^Tn^*| + |\alpha ^T(s_t - s^*)|) \nonumber \\&\times \sum _{k=0}^{\infty } c^TA^{k}b \le \sum _{t=0}^{\infty }\alpha _1 p_2|c^TA^t(n_0-n^*)| \nonumber \\&+ \frac{\alpha _1p_2m_1}{p_e}\sum _{t=0}^M(\alpha _1m_2|c^Tn_t -c^Tn^*| + |\alpha ^T(s_t - s^*)|).\nonumber \\ \end{aligned}$$

(6.19)

The $X_2$ component of $\tilde{n}_t$ satisfies

$$\begin{aligned} s_t = \left( \sum _{j=0}^{t-1}S^{t - j - 1}\Gamma _1 h(c^TA^{j}n_0 + \sum _{k=0}^{j - 1}c^TA^{j -k - 1}bf(\tilde{y}_{k}))\right) + S^ts_0, \end{aligned}$$

(6.20)

where $\Gamma _1 := [\gamma _1 \; \; 0\, \cdots \,0]^T$. Since

$$\begin{aligned} c^TA^{j}n_0 + \sum _{k=0}^{j - 1}c^TA^{j -k - 1}bf(\tilde{y}_{k})) = c^Tn_j \end{aligned}$$

it follows that

$$\begin{aligned} s_t = \left( \sum _{j=0}^{t-1}S^{t - j - 1}\Gamma _1 h(c^Tn_j)\right) + S^ts_0. \end{aligned}$$

(6.21)

Since $\tilde{n}^*$ was is a fixed point of our system, if we insert $[n^* \; \; s^*]^T$ for $[n _0 \; \; s_0]^T$ in (6.20) we obtain

$$\begin{aligned} s^*&= \left( \sum _{j=0}^{t-1}S^{t - j - 1}\Gamma _1 h(c^TA^{j}n^* + \sum _{k=0}^{j - 1}c^TA^{j -k - 1}bf(y^*))\right) + S^ts^* \nonumber \\&= \left( \sum _{j=0}^{t-1}S^{t - j - 1}\Gamma _1 h(c^Tn^*)\right) + S^ts^*. \end{aligned}$$

(6.22)

Thus, subtracting (6.22) from (6.21), and multiplying by $\alpha ^T$ on the left gives us

$$\begin{aligned} \alpha ^T(s_t - s^*) \!=\! \left( \sum _{j=0}^{t-1}\alpha ^T S^{t - j - 1}\Gamma _1( h(c^Tn_j) \!-\! h(c^Tn^*))\right) \!+\! \alpha ^TS^t(s_0 \!-\! s^*), \end{aligned}$$

(6.23)

Using (6.12), and the positivity of the system, we have that

$$\begin{aligned} |\alpha ^T(s_t \!-\! s^*)| \!\le \! \left( \sum _{j=0}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1m_2|c^Tn_j \!-\! c^Tn^*|\right) \!+\! |\alpha ^TS^t(s_0 - s^*)|. \end{aligned}$$

(6.24)

Putting

$$\begin{aligned} c^Tn_j = c^TA^{j}n_0 + \sum _{k=0}^{j - 1}c^TA^{j -k - 1}bf(\tilde{y}_{k}) \end{aligned}$$

and

$$\begin{aligned} c^Tn^* = c^TA^{j}n^* + \sum _{k=0}^{j - 1}c^TA^{j -k - 1}bf(y^*) \end{aligned}$$

back into (6.24) we obtain

$$\begin{aligned} |\alpha ^T(s_t - s^*)|&\le \left( \sum _{j=0}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1m_2| c^TA^{j}n_0 + \sum _{k=0}^{j - 1}c^TA^{j -k - 1}bf(\tilde{y}_{k}) - c^TA^{j}n^* \right. \\&\quad \left. + \sum _{k=0}^{j - 1}c^TA^{j -k - 1}bf(y^*)|\right) +|\alpha ^TS^t(s_0 - s^*)|\\&\le |\alpha ^TS^t(s_0 - s^*)| + m_2\sum _{j=0}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1|c^TA^{j}(n_0 - n^*)| \\&\quad + m_2\sum _{j=0}^{t-1}\sum _{k=0}^{j - 1}\alpha ^TS^{t - j - 1}\Gamma _1 c^TA^{j -k - 1}b|f(\tilde{y}_{k}) - f(y^*)|. \end{aligned}$$

Summing from $t = 0$ to $M$, for $M$ large, and rearranging we have

$$\begin{aligned} \sum _{t=0}^M|\alpha ^T(s_t - s^*)|&\le \sum _{t=0}^M|\alpha ^TS^t(s_0 - s^*)| + m_2\sum _{t=0}^M\sum _{j=0}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1|c^TA^{j}n_0 - n^*|\\&+ m_2\sum _{k=0}^{M - 2}|f(\tilde{y}_{k}) - f(y^*)|\sum _{t=k + 2}^{M}\sum _{j=k+1}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1 c^TA^{j -k - 1}b \end{aligned}$$

Adding more terms and changing indices, we have

$$\begin{aligned} \sum _{t=0}^M|\alpha ^T(s_t - s^*)|&\le \sum _{t=0}^M|\alpha ^TS^t(s_0 - s^*)| + m_2\sum _{t=0}^M\sum _{j=0}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1|c^TA^{j}n_0 - n^*| \\&+ m_2\sum _{t=0}^{M}|f(\tilde{y}_{t}) - f(y^*)|\sum _{j=0}^{\infty }\alpha ^TS^{j}\Gamma _1\sum _{k=0}^{\infty } c^TA^{k}b. \end{aligned}$$

Using (6.12) again,

$$\begin{aligned} \sum _{t=0}^M|\alpha ^T(s_t - s^*)|&\le \sum _{t=0}^M|\alpha ^TS^t(s_0 - s^*)| + m_2\sum _{t=0}^M\sum _{j=0}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1|c^TA^{j}(n_0 - n^*)| \\&\quad + m_1m_2\sum _{t=0}^{M}|\tilde{y}_{t}- y^*|\sum _{j=0}^{\infty }\alpha ^TS^{j}\Gamma _1\sum _{k=0}^{\infty } c^TA^{k}b \\&\le \sum _{t=0}^M|\alpha ^TS^t(s_0 - s^*)| + m_2\sum _{t=0}^M\sum _{j=0}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1|c^TA^{j}(n_0 - n^*)| \\&\quad + m_1m_2\sum _{t=0}^{M}|\alpha _1h(c^Tn_t )+ \alpha ^Ts_t - \alpha _1h(c^Tn^*) \\&\quad -\alpha ^Ts^*|\sum _{j=0}^{\infty }\alpha ^TS^{j}\Gamma _1\sum _{k=0}^{\infty } c^TA^{k}b. \end{aligned}$$

Using the triangle inequality, as well as (6.12) again,

$$\begin{aligned} \sum _{t=0}^M|\alpha ^T(s_t - s^*)|&\le \sum _{t=0}^M|\alpha ^TS^t(s_0 - s^*)| + m_2\sum _{t=0}^M\sum _{j=0}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1|c^TA^{j}(n_0 - n^*)| \\&\quad +m_1 m_2\sum _{t=0}^{M}(\alpha _1m_2|c^Tn_t - c^Tn^*| + |\alpha ^T(s_t -s^*)|) \\&\quad \times \sum _{j=0}^{\infty }\alpha ^TS^{j}\Gamma _1\sum _{k=0}^{\infty } c^TA^{k}b. \end{aligned}$$

Since $\sum _{j=0}^{\infty }S^j= (I - S)^{-1}$ and $\sum _{k=0}^{\infty }A^k= (I - A)^{-1}$ we have

$$\begin{aligned}&\sum _{t=0}^M|\alpha ^T(s_t {-} s^*)| \le \sum _{t=0}^M|\alpha ^TS^t(s_0 - s^*)| + m_2\sum _{t=0}^M\sum _{j=0}^{t-1}\alpha ^TS^{t - j - 1}\Gamma _1|c^TA^{j}(n_0 - n^*)| \nonumber \\&\qquad \qquad \qquad \qquad \quad + \frac{m_1 m_2\alpha ^T(I - S)^{-1}\Gamma _1}{p_e}\sum _{t=0}^{M}(\alpha _1m_2|c^Tn_t - c^Tn^*|\nonumber \\&\qquad \qquad \qquad \qquad \quad + |\alpha ^T(s_t -s^*)|) \end{aligned}$$

(6.25)

The first two terms of (6.25) converge as $M \rightarrow \infty$, since $r(A) < 1$ and $\gamma _i < 1$ for all $i$. Define

$$\begin{aligned} L&:= \sum _{t=0}^{\infty } \alpha _1p_2|c^TA^t(n_0 - n^*)| + \sum _{t=0}^{\infty }|\alpha ^{T} S^{t}(s_0 - s^*)| \\&\quad + m_2\sum _{k=0}^{\infty }\sum _{j=0}^{k}S^{j}\Gamma _1 |c^{T} {A}^{k} (n_0 - n^*)| < \infty . \end{aligned}$$

Adding the (6.19) and (6.25) together, we obtain

$$\begin{aligned} \sum _{t=0}^M(|\alpha _1p_2c^T(n_t \!-\! n^*)| \!+\! |\alpha ^T(s_t \!-\! s^*)|)&\le L + \frac{\alpha _1p_2m_1 + m_2m_1\alpha ^T(I - S)^{-1}\Gamma _1}{p_e} \\&\times \sum _{t=0}^M (\alpha _1m_2|c^Tn_t \!-\!c^Tn^*| \!+\! |\alpha ^T(s_t \!-\! s^*)|). \end{aligned}$$

Since $m_1 < p_1$ and $m_2 < p_2$, and using (3.7) there exists an $m < 1$ such that

$$\begin{aligned} \frac{\alpha _1p_2m_1 + m_2m_1\alpha ^T(I - S)^{-1}\Gamma _1}{p_e} \le p_2m_1\frac{\alpha _1+\alpha ^T(I - S)^{-1}\Gamma _1}{p_e}\le \frac{p_2 m_1}{p_1 p_2} \le m < 1. \end{aligned}$$

Hence

$$\begin{aligned}&\sum _{t=0}^M(|\alpha _1p_2c^T(n_t - n^*)| + |\alpha ^T(s_t - s^*)|) \\&\le L + m\sum _{t=0}^M (\alpha _1m_2|c^Tn_t -c^Tn^*| + |\alpha ^T(s_t - s^*)|), \end{aligned}$$

which implies that

$$\begin{aligned} \sum _{t=0}^M(|\alpha _1(p_2 - m_2)c^T(n_t - n^*)| + |\alpha ^T(s_t - s^*)|)\le (1-m)^{-1}L \end{aligned}$$

(6.26)

This bound is independent of $M$. Therefore the sequence

$$\begin{aligned} \{\alpha _1c^T(n_t - n^*)| + |\alpha ^T(s_t - s^*)|\}_{t=0}^{\infty } \in \ell _1(\mathbb N ), \end{aligned}$$

so

$$\begin{aligned} \lim _{t \rightarrow \infty }(|\alpha _1c^T(n_t - n^*)| + |\alpha ^T(s_t - s^*)|)=0, \end{aligned}$$

(6.27)

which, by the continuity of $h$, implies that

$$\begin{aligned} \lim _{t \rightarrow \infty }|\tilde{y}_t - y^*|=0. \end{aligned}$$

(6.28)

By (6.13), (6.28) and assumptions (E1) and (E4) we therefore have that

$$\begin{aligned} \lim _{t \rightarrow \infty }\tilde{n}_t = \tilde{n}^*, \end{aligned}$$

(6.29)

as sought. The $(\epsilon , \delta )$ conclusion follows from Holder’s inequality and assumption $(E1)$. $\square$

Fig. 6

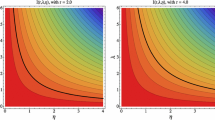
Example nonlinearities $f$ or $h$ which satisfy (D1) with sectors defined by lines with slopes $\pm p_1$ or $\pm p_2$ (dotted), showing how (6.12) holds

Appendix B

Proof of Theorem 3.3

The proof of (1) is identical to the proof of (1) in Theorem 3.2.

For (2) note that if there exists a solution $(p_1, p_2, y^*)$ of (3.10) in $(0,g_0)\times (\exp (-2),1)\times (0,\infty )$ and $m > 0$ such that $\tilde{y}_t > m$ and $c^Tn_t \ge m$ for all $t \in \mathbb{N }$, then $h_R$ is sector bounded as in (3.11) (Fig. 2). This follows from the fact that

$$\begin{aligned} h_R^{\prime }(y) = (1 - \frac{y}{c_m})\mathrm exp (-y/c_m), \quad h_R^{\prime \prime }(y) = \frac{1}{c_m}(\frac{y}{c_m} - 2)\mathrm exp (-y/c_m). \end{aligned}$$

Thus $h_R$ has $\mathrm exp (-2)$ as its maximum negative slope. If $\tilde{y}_t$ and $c^Tn_t$ are uniformly bounded away from $0$, $h_R$ satisfies

$$\begin{aligned} |h_R(c^Tn_t) - h_R(c^Tn^*)| \le m_2|c^Tn_t - c^Tn^*|\; \end{aligned}$$

for some $m_2 < p_2$. To see that there exists $m > 0$ such that $\tilde{y}_t\ge m$ and $c^Tn_t \ge m$ for all $t \in \mathbb{N }$, we note that if $\tilde{y}_t \le y^*$ and $c^Tn_t \le c^Tn^*$ or $\tilde{y}_t \ge y^*$ the lower bound follows as in Theorem 3.2. If $\tilde{y}_t \le y^*$ and $c^Tn_t \ge c^Tn^*$ we need to show that the solution $\{\tilde{n}_t\}_{t=0}^{\infty }$ is bounded above. Noting that $f(y) \le f(y^*) + m_1y$ for some $m_1 < p_1$ and $y \ge 0$ and $h_R(y) \le c_m\mathrm exp (-1)$ for all $y \ge 0$, it follows that

$$\begin{aligned} \tilde{c}_1^T\tilde{n}_t \le \tilde{c}_1^T\hat{A}\tilde{n}_{t-1} + c^Tbf(y^*) + (m_1c^Tb + \gamma _1)c_m\mathrm exp (-1): = \tilde{c}_1^T\hat{A}\tilde{n}_{t-1} + K, \end{aligned}$$

where

$$\begin{aligned} \hat{A}:= \left[ {\begin{array}{lc} A &{} B_{m_1} \\ \Gamma _{0} &{} S \\ \end{array} } \right] , \quad B_{m_1}:= \left[ \begin{array}{cccc} m_1b&m_1b&\cdots&m_1b \end{array} \right] , \end{aligned}$$

and $r(\hat{A}) <1$. Thus $\tilde{c}_1^T\tilde{n}_t \le M$ for some $M < \infty$, which implies that $c^Tn_t \le M/\alpha _1$ for all $t \ge 0$. Thus, if $\tilde{y}_t \le y^*$ and $c^Tn_t \ge c^Tn^*$ we have that $f(\tilde{y}_t) \ge f(y^*)$ and $h_R(c^Tn_t) > \mathrm min \{h_R(c^Tn^*), h_R(M/\alpha _1)\} > 0$. Letting $\tilde{w}_{p_2}^T$ be defined as in Theorem 3.2,

$$\begin{aligned} \tilde{w}_{p_2}^T\tilde{n}_t \ge \mathrm min \{\tilde{w}_{p_2}^T\tilde{n}_0,\; p_2p_1\alpha _1\tilde{w}_{p_2}^T\tilde{b}c^Tn^*,\; \tilde{w}_{p_2}^T\tilde{b}p_1h_R(M/\alpha _1)\}, \end{aligned}$$

(7.1)

thus $\tilde{y}_t$, and similarly $c^Tn_t$, are bounded from below as in Theorem 3.2. The remainder of the proof for (2) is the same as in Theorem 3.2.

For part (3) note that

$$\begin{aligned} h_R^{\prime }(c^Tn^*) = p_2(1 + \mathrm ln (p_2))< - p_2, \end{aligned}$$

(7.2)

so we cannot sector-bound $h_R$ as we did in (2) of this theorem. The linearization about $\tilde{n}^*$ yields

$$\begin{aligned} \tilde{n}_{t+1} \simeq (\tilde{A}_{(1 + \mathrm ln (p_2))p_2} + f^{\prime }(y^*) \tilde{b}\tilde{c}_{(1 +\mathrm ln (p_2))p_2}^T)\tilde{n}_t. \end{aligned}$$

Thus if $r(\tilde{A}_{(1 +\ln (p_2))p_2} + f^{\prime }(y^*) \tilde{b}\tilde{c}_{(1 +\ln (p_2))p_2}^T) < 1$ then $\tilde{n}^*$ is asymptotically stable, as sought. $\square$

Appendix C

Proof of Corollary 3.1

To prove (1) we need to show that $(\tilde{A},\tilde{b},\tilde{c})$ satisfies hypotheses (A1), (A2) and (A3) in Rebarber et al. (2012). We verified that (A1) and (A2) are met by $\tilde{A}$ and $\tilde{b}$ in the proof of Theorem 3.1. To prove that (A3) is met by $\tilde{c}^T$, note that (3.16) implies that $c^Tn \ge 0$ for all $n \in X_1$. This, coupled with (E4) implies that $\tilde{c}^T\tilde{n} \ge 0$ for all $\tilde{n} \in X_1 \otimes X_2$, proving (1).

To prove (2) and (3) note that (E3) is only used in the proof of Theorem 3.2 (2) and Theorem 3.3 (2), i.e. when $\tilde{n}^*$ is positive and globally stable. Also, the only place where we needed to use (E3) in the proofs of Theorems 3.2 and 3.3 is where we assert that there exists an $m > 0$ such that $\tilde{y_t},c^Tn_t \ge m$ for all $t \ge 0$. To prove this in the case where $h$ is continuous, increasing, concave down, with $h(0) = 0$, we introduce a new IPM system which is “close”’ to the original system (2.7). For $\epsilon >0$, let $I_{\epsilon }:=\{x \in [L,U]| c(x) > \epsilon \}, X_{1,\epsilon }:= L^1(I_{\epsilon })$ and $A_{\epsilon }:X_{1,\epsilon } \rightarrow X_{1,\epsilon }$ be such that

$$\begin{aligned} A_{\epsilon }n = \int _{I_\epsilon } k(x,y)n(y)\;dy, \end{aligned}$$

with $b_{\epsilon } = b|_{I_\epsilon }$ and

$$\begin{aligned} c^T_{\epsilon }n = \int _{I_{\epsilon }} c(y)n(y)\;dy. \end{aligned}$$

It follows that $r(A_{\epsilon }) \le r(A) < 1$, so $A_{\epsilon }$ satisfies (E1). It’s straightforward that, for sufficiently small $\epsilon$, $b_{\epsilon }$ satisfies (E2) and that $c_\epsilon ^T$ satisfies (E3) with $c_{\min } = \epsilon$. Let

$$\begin{aligned} p_e(\epsilon ) = (c_\epsilon ^T(I - A_\epsilon )^{-1}b_\epsilon )^{-1}. \end{aligned}$$

It follows that $\lim _{\epsilon \rightarrow 0}p_e(\epsilon ) = p_e$. Since in Theorem 3.2 (2) the system of Eqs. (3.10) has a solution $(p_1,p_2,y^*) \in (0,g_0)\times (0,1)\times (0,\infty )$, we can choose $\epsilon >0$ such that the system of equations

$$\begin{aligned} g(y^*(\epsilon ))&= p_1(\epsilon ) \\ p_1(\epsilon )p_2(\epsilon )&= \frac{p_e(\epsilon )}{(\alpha _1 + \alpha ^T(I - S)^{-1}\Gamma _1)}\\ h\left( \frac{p_1(\epsilon ) y^*(\epsilon )}{p_e(\epsilon )}\right)&= \frac{p_2(\epsilon )p_1(\epsilon )y^*(\epsilon )}{p_e(\epsilon )}. \end{aligned}$$

has a solution $(p_1(\epsilon ),p_2(\epsilon ),y^*(\epsilon )) \in (0,g_0)\times (0,1)\times (0,\infty )$. Let $[n(\epsilon )_t \; \; s(\epsilon )_t]^T \subset X_{\epsilon }:= X_{1,\epsilon }\otimes X_2$ solve

$$\begin{aligned} n(\epsilon )_{t+1}&= A_\epsilon n(\epsilon )_t + b_\epsilon f(\tilde{y}(\epsilon )_t), \\ \tilde{y}(\epsilon )_t&= \alpha _1h(c^T_\epsilon n(\epsilon )_t) + \alpha _2s(\epsilon )_{1,t} +\cdots +\alpha _{N+1}s(\epsilon )_{N,t} \\ s(\epsilon )_{1,t + 1}&= \gamma _{1}h(c_\epsilon ^T n(\epsilon )_t)\\ s(\epsilon )_{2,t+1}&= \gamma _{2}s(\epsilon )_{1,t}\\&\vdots&\\ s(\epsilon )_{N-1,t+1}&= \gamma _{N-1}s(\epsilon )_{N-2,t}\\ s(\epsilon )_{N,t + 1}&= \gamma _{N}s(\epsilon )_{N - 1,t} + \gamma _{N + 1 }s(\epsilon )_{N,t}. \end{aligned}$$

Since $(p_1(\epsilon ),p_2(\epsilon ),y^*(\epsilon )) \in (0,g_0)\times (0,1)\times (0,\infty )$ we have, by the proof of Theorem 3.2, the existence of an $m >0$ such that $\tilde{y}(\epsilon ), c_\epsilon ^Tn(\epsilon )_t \ge m$ for all $t \ge 0$. By the monotonicity of $f$ and $h$ and the positivity of $(A,b,c)$, $\{\alpha _j\}_{j=1}^{N+1}$ and $\{\gamma _j\}_{j=1}^{N+1}$ we have $\tilde{y}_t \ge \tilde{y}(\epsilon )_t$ and $c^Tn_t \ge c_\epsilon ^Tn(\epsilon )_t$ for all $t \ge 0$. Thus there exists an $m >0$ such that $\tilde{y}, c^Tn_t \ge m$ for all $t \ge 0$ and (2) is proved.

For (3) $h(y)$ is equal to $h_R(y) = y e^{-y/c_m}$, which is not monotone once $y$ becomes larger than $c_m$. Thus we cannot bound $\tilde{y}_t$ and $c^Tn_t$ from below by $\tilde{y}(\epsilon )_t$ and $c(\epsilon )^Tn(\epsilon )_t$ for all $t \ge 0$, unless $c^Tn_t$ does not exceed $c_m$ for all $t \ge 0$.

In the proof of Theorem 3.3, we showed that there exists an $M >0$ (which depends on $\tilde{n}_0$) such that $\tilde{c}^T_1\tilde{n}_t \le M$ for all $t \ge 0$, which implies that $c^Tn_t \le M/\alpha _1$ for all $t \ge 0$. If $M/\alpha _1 \le c_m$ we can use the same arguments as in (2), due to the monotonicity of $h_R(y)$ for $y \le c_m$. If $M/\alpha _1 > c_m$ we will construct a seed production function $\underline{h}$ that is continuous, increasing, concave down, with $\underline{h}(0) = 0, \underline{h}^{\prime }(0) = 1$ such that $\underline{h}(y) \le h_R(y)$ for all $y \in [0,M/\alpha _1]$. The population in a model with $\underline{h}$ instead of $h_R$ will be smaller than $\tilde{n}_t$ for all $t \ge 0$. If this smaller population has a nonzero globally stable equilibrium population than we will have our desired lower bound.

Define the function

$$\begin{aligned} \underline{h}(y) = \frac{M y}{M + \alpha _1\left( e^{\frac{M}{\alpha _1 c_m}} - 1\right) y}, \end{aligned}$$

which is continuous, increasing, concave down, with $\underline{h}(0) = h_R(0) = 0, \underline{h}^{\prime }(0) = h_R^{\prime }(0) = 1$ and $\underline{h}(M/\alpha _1) = h_R(M/\alpha _1) = M/\alpha _1 e^{-\frac{M}{\alpha _1 c_m}}$. Since $c_m < M/\alpha _1$ implies that

$$\begin{aligned} \underline{h}^{\prime \prime }(0) = \frac{2\alpha _1 \left( e^{\frac{M}{\alpha _1 c_m}} - 1 \right) }{M} <\frac{-2}{c_m} = h_R^{\prime \prime }(0), \end{aligned}$$

we have that $\underline{h}(y) \le h_R(y)$ for all $y \in [0,M/\alpha _1]$ (see Fig. 7). Let $\tilde{\underline{n}}_t = [\underline{n}_t \; \; \underline{s}_t]^T \subset X$ solve

$$\begin{aligned} \underline{n}_{t+1}&= A \underline{n}_t + bf(\underline{y}_t), \\ \underline{y}_t&= \alpha _1\underline{h}(c^T\underline{n}_t) + \alpha _2\underline{s}_{1,t} + \cdots +\alpha _{N+1}\underline{s}_{N,t}\\ \underline{s}_{1,t + 1}&= \gamma _{1}h(c^T \underline{n}_t)\\ \underline{s}_{2,t+1}&= \gamma _{2}\underline{s}_{1,t}\\&\vdots&\\ \underline{s}_{N-1,t+1}&= \gamma _{N-1}\underline{s}_{N-2,t}\\ \underline{s}_{N,t + 1}&= \gamma _{N}\underline{s}_{N - 1,t} + \gamma _ {N + 1 }\underline{s}_{N,t}. \end{aligned}$$

It follows that, if $\tilde{\underline{n}}_0 = \tilde{n}_0$, we have that $\tilde{\underline{n}}_t \le \tilde{n}_t$, and thus $c^T\underline{n}_t \le c^Tn_t$, for all $t \ge 0$. Since in Theorem 3.3 (2) the sytem of Eqs. (3.10) has a solution $(p_1,p_2,y^*) \in (0,g_0)\times (e^{-2},1)\times (0,\infty )$ it follows that the system of equations

$$\begin{aligned} g(\underline{y}^*)&= \underline{p}_1 \\ \underline{p}_1\underline{p}_2&= \frac{p_e}{(\alpha _1 + \alpha ^T(I - S)^{-1}\Gamma _1)}\\ \underline{h}\left( \frac{\underline{p}_1 \underline{y}^{*}}{p_e}\right)&= \frac{\underline{p}_2\underline{p}_1\underline{y}^*}{p_e}. \end{aligned}$$

has a solution $(\underline{p}_1,\underline{p}_2,\underline{y}^*) \in (0,g_0)\times (0,1)\times (0,\infty )$ (see Fig. 7). This implies, from the above proof of (2), that $\tilde{\underline{n}}_t$ converges to a positive, globally stable equilibrium population $\tilde{\underline{n}}^*$. Since $\tilde{n}_t \ge \tilde{\underline{n}}_t$ for all $t \ge 0$ we have the desired positive lower bound $m$ for $\tilde{y}_t$ and $c^Tn_t$, proving (3). $\square$

Fig. 7

An example of the comparison between $h_R$ and the increasing, convace down $\underline{h}$, with $M/\alpha _1 = 6$. Notice that if the equation $h_R(y) = p_2 y$ has a solution ($p_2, y) \in (e^{-2},1)\times (0,\infty )$, then the equation $\underline{h}(y) = p_2 y$ has a solution in $(0,1)\times (0,\infty )$, as $h_R(0) = \underline{h}(0) = 0$ and $h_R^{\prime }(0) = \underline{h}^{\prime }(0) = 1$