Thermoelastic model of minerals: application to Al₂O₃

Abstract

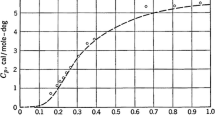
 A thermoelastic model for calculating the high-pressure and high-temperature properties of isotropic solids is presented by extending the formalism by Thomsen and combining the resulting one with the Vinet model for static lattice and the Debye model for lattice vibration. Applying it to polycrystalline corundum, we have shown that the calculated values of entropy and heat capacity at constant pressure are in agreement with literature values to 2325 K at zero pressure and that the calculated values of thermal expansivity agree reasonably with experimental data to 1100 K at zero pressure. The model reproduces experimental data of sound velocities v _p and v _s of compressional and shear waves to 1825 K at zero pressure and those to 62 GPa at room temperature, and it reproduces also experimental shock-wave equation of state to 150 GPa. The velocity correlation (∂ln v _s /∂ln v _p ) _S was found to have weak pressure and temperature dependences and the results under lower mantle conditions are compared with those of magnesian and calcium silicate perovskites and magnesiowüstite, and the PREM values of the Earth's lower mantle.