Skip to main content
SpringerLink
Log in

Long-Time Behavior of a Nonlinearly-Damped Three-Layer Rao–Nakra Sandwich Beam

  • Published:
Applied Mathematics & Optimization Aims and scope Submit manuscript

Abstract

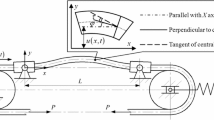
In this paper, a three-layer Rao–Nakra sandwich beam is considered where the core viscoelastic layer is constrained by the purely elastic or piezoelectric outer layers. In the model, uniform bending motions of the overall laminate are coupled to the longitudinal motions of the outer layers, and the shear of the middle layer contributes to the overall motion. Together with nonlinear damping injection and nonlinear source terms, the existence and uniqueness of local and global weak solutions are obtained by the nonlinear semigroup theory and the theory of monotone operators. The global existence of potential well solutions and the uniform energy decay rates of such a solution, given as a solution to a certain nonlinear ODE, are shown are proved under certain assumptions of the parameters and by the Nehari manifold. Finally, the existence of a smooth global attractor with finite fractal dimension, which is characterized as an unstable manifold of the set of stationary solutions, and exponential attractors for the associated dynamical system are proved. The present paper extends the linear analysis of the stability of the Rao–Nakra sandwich beam to nonlinear analysis in the existing literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Allen, A.A.: Stability results for damped multilayer composite beams and plates. Ph.D. Thesis, Iowa State University (2009)

  2. Alves, C.O., Cavalcanti, M.M., Cavalcanti, V.N.D., Rammaha, M.A., Toundykov, D.: On existence, uniform decay rates and blow up for solutions of systems of nonlinear wave equations with damping and source terms. Discrete Contin. Dyn. Syst. Ser. S 2(3), 583–608 (2009)

    MathSciNet  MATH  Google Scholar 

  3. Aouadi, M.: Regularity and upper semicontinuity of pullback attractors for non-autonomous Rao–Nakra beam. Nonlinearity 35, 1773 (2022)

    MathSciNet  MATH  Google Scholar 

  4. Baz, A.: Boundary control of beams using active constrained layer damping. J. Vib. Acoust. 119, 166–172 (1997)

    Google Scholar 

  5. Babin, A.V., Vishik, M.I.: Attractors of Evolution Equations. Studies in Mathematics and Its Application, vol. 25. North-Holland, Amsterdam (1992)

    Google Scholar 

  6. Barbu, V.: Nonlinear Differential Equations of Monotone Types in Banach Spaces. Springer, New York (2010)

    MATH  Google Scholar 

  7. Barbu, V.: Analysis and Control of Nonlinear Infinite-Dimensional Systems, Mathematics in Science and Engineering, vol. 190. Academic Press, Boston (1993)

    Google Scholar 

  8. Bociu, L.: Local and global wellposedness of weak solutions for the wave equation with nonlinear boundary and interior sources of supercritical exponents and damping. Nonlinear Anal. 71(12), 560–575 (2009)

    MathSciNet  MATH  Google Scholar 

  9. Bociu, L., Lasiecka, I.: Blow-up of weak solutions for the semilinear wave equations with nonlinear boundary and interior sources and damping. Appl. Math. (Warsaw) 35(3), 281–304 (2008)

    MathSciNet  MATH  Google Scholar 

  10. Bociu, L., Lasiecka, I.: Uniqueness of weak solutions for the semilinear wave equations with supercritical boundary/interior sources and damping. Discrete Contin. Dyn. Syst. 22(4), 835–860 (2008)

    MathSciNet  MATH  Google Scholar 

  11. Bociu, L., Lasiecka, I.: Local Hadamard well-posedness for nonlinear wave equations with supercritical sources and damping. J. Differ. Equ. 249(3), 654–683 (2010)

    MathSciNet  MATH  Google Scholar 

  12. Bociu, L., Radu, P.: Existence of weak solutions to the Cauchy problem of a semilinear wave equation with supercritical interior source and damping. Discrete Contin. Dyn. Syst. (2009), No. Dynamical Systems, Differential Equations and Applications. 7th AIMS Conference, Suppl., pp. 60–71

  13. Bociu, L., Rammaha, M., Toundykov, D.: On a wave equation with supercritical interior and boundary sources and damping terms. Math. Nachr. 284, 2032–2064 (2011)

    MathSciNet  MATH  Google Scholar 

  14. Brezis, H.: Integrales convexes dans les espaces de Sobolev. Isr. J. Math. 13, 9–23 (1972)

    MathSciNet  Google Scholar 

  15. Chueshov, I., Eller, M., Lasiecka, I.: On the attractor for a semilinear wave equation with critical exponent and nonlinear boundary dissipation. Commun. Partial Differ. Equ. 27, 1901–1951 (2002)

    MathSciNet  MATH  Google Scholar 

  16. Chueshov, I., Lasiecka, I.: Long-time behavior of second order evolution equations with nonlinear damping. Mem. Am. Math. Soc. 195, 912 (2008)

    MathSciNet  MATH  Google Scholar 

  17. Chueshov, I., Lasiecka, I.: Von Karman Evolution Equations: Well-Posedness and Long-Time Dynamics. Springer Monographs in Mathematics. Springer, New York (2010)

    MATH  Google Scholar 

  18. Georgiev, V., Todorova, G.: Existence of a solution of the wave equation with nonlinear damping and source terms. J. Differ. Equ. 109, 295–308 (1994)

    MathSciNet  MATH  Google Scholar 

  19. Guo, Y., Rammaha, M.A.: Systems of nonlinear wave equations with damping and supercritical sources. Trans. Am. Math. Soc. 366(5), 2265–2325 (2014)

    MathSciNet  MATH  Google Scholar 

  20. Guo, Y., Rammaha, M.A., Sakuntasathien, S., Titi, E.S., Toundykov, D.: Hadamard well-posedness for a hyperbolic equation of viscoelasticity with supercritical sources and damping. J. Differ. Equ. 257, 3778–3812 (2014)

    MathSciNet  MATH  Google Scholar 

  21. Guo, Y., Rammaha, M.A.: Global existence and decay of energy to systems of wave equations with damping and supercritical sources. Z. Angew. Math. Phys. 64(3), 621–658 (2013)

    MathSciNet  MATH  Google Scholar 

  22. Hale, J.K.: Asymptotic Behavior of Dissipative Systems. Mathematical Surveys and Monographs, vol. 25. American Mathematical Society, Providence (1988)

    Google Scholar 

  23. Hansen, S.W.: Several related models for multilayer sandwich plates. Math. Models Methods Appl. Sci. 14, 1103–1132 (2004)

    MathSciNet  MATH  Google Scholar 

  24. Hansen, S.W., Imanuvilov, O.Y.: Exact controllability of a multilayer Rao–Nakra plate with free boundary conditions. Math. Control Relat. Fields 1, 189–230 (2011)

    MathSciNet  MATH  Google Scholar 

  25. Hansen, S.W., Imanuvilov, O.Y.: Exact controllability of a multilayer Rao–Nakra plate with clamped boundary conditions. ESAIM Control Optim. Calc. Var. 17, 1101–1132 (2011)

    MathSciNet  MATH  Google Scholar 

  26. Hansen, S.W., Rajaram, R.: Riesz basis property and related results for a Rao–Nakra sandwich beam. Discrete Contin. Dyn. Syst. 2005, 365–375 (2005)

    MathSciNet  MATH  Google Scholar 

  27. Hansen, S.W., Rajaram, R.: Simultaneous boundary control of a Rao–Nakra sandwich beam. In: Proceedings of the 44th IEEE Conference on Decision and Control and European Control Conference, pp. 3146–3151 (2005)

  28. Horn, M.A., Lasiecka, I.: Asymptotic behavior with respect to thickness of boundary stabilizing feedback for the Kirchhoff plate. J. Differ. Equ. 114(2), 396–433 (1994)

    MathSciNet  MATH  Google Scholar 

  29. Koch, H., Lasiecka, I.: Hadamard well-posedness of weak solutions in nonlinear dynamic elasticity-full Von Karman systems. In: Evolution Equations, Semigroups and Functional Analysis. Progress in Nonlinear Differential Equations and Their Applications, vol. 50. Birkhäuser, Basel (2002)

  30. Lakshmikantham, V., Leela, S.: Differential and Integral Inequalities: Theory and Applications. Vol. I: Ordinary Differential Equations, Mathematics in Science and Engineering. Academic Press, New York (1969)

    MATH  Google Scholar 

  31. Lasiecka, I., Tataru, D.: Uniform boundary stabilization of semilinear wave equations with nonlinear boundary damping. Differ. Integr. Equ. 6(3), 507–533 (1993)

    MathSciNet  MATH  Google Scholar 

  32. Li, Y., Liu, Z., Wang, Y.: Weak stability of a laminated beam. Math. Control Relat. Fields 8, 789–808 (2018)

    MathSciNet  MATH  Google Scholar 

  33. Liu, Z., Rao, B., Zheng, Q.: Polynomial stability of the Rao–Nakra beam with a single internal viscous damping. J. Differ. Equ. 269, 6125–6162 (2020)

    MathSciNet  MATH  Google Scholar 

  34. Ma, T.F., Monteiro, R.N.: Singular limit and long-time dynamics of Bresse systems. SIAM J. Math. Anal. 49(4), 2468–2495 (2017)

    MathSciNet  MATH  Google Scholar 

  35. Nehari, Z.: On a class of nonlinear second-order differential equations. Trans. Am. Math. Soc. 95(1), 101–123 (1960)

    MathSciNet  MATH  Google Scholar 

  36. Nehari, Z.: Characteristic values associated with a class of nonlinear second-order differential equations. Acta Math. 105(3–4), 141–175 (1961)

    MathSciNet  MATH  Google Scholar 

  37. Özer, A.Ö., Hansen, S.W.: Uniform stabilization of a multi-layer Rao–Nakra sandwich beam. Evol. Equ. Control Theory 2, 695–710 (2013)

    MathSciNet  MATH  Google Scholar 

  38. Özer, A.Ö.: Modeling and well-posedness results for active constrained layered (ACL) beams with/without magnetic effects. In: Proceedings of the SPIE 9799, Active and Passive Smart Structures and Integrated Systems, 97991F (2016)

  39. Özer, A.Ö., Hansen, S.W.: Exact boundary controllability results for a multilayer Rao–Nakra sandwich beam. SIAM J. Cont. Optim. 52, 1314–1337 (2014)

    MathSciNet  MATH  Google Scholar 

  40. Özer, A.Ö.: Modeling and controlling an active constrained layered (ACL) beam actuated by two voltage sources with/without magnetic effects. IEEE Trans. Autom. Control 62, 6445–6450 (2017)

    MATH  Google Scholar 

  41. Özer, A.Ö.: Potential formulation for charge or current-controlled piezoelectric smart composites and stabilization results: electrostatic versus quasi-static versus fully-dynamic approaches. IEEE Trans. Autom. Control 64–3, 989–1002 (2018)

    MathSciNet  MATH  Google Scholar 

  42. Pei, P., Rammaha, M.A., Toundykov, D.: Local and global well-posedness of semilinear Reissner–Mindlin–Timoshenko plate equations. Nonlinear Anal. 105, 62–85 (2014)

    MathSciNet  MATH  Google Scholar 

  43. Pei, P., Rammaha, M.A., Toundykov, D.: Global well-posedness and stability of semilinear Mindlin–Timoshenko system. J. Math. Anal. Appl. 418, 535–568 (2014)

    MathSciNet  MATH  Google Scholar 

  44. Rajaram, R.: Exact boundary controllability result for a Rao–Nakra sandwich beam. Syst. Control Lett. 56, 558–567 (2007)

    MathSciNet  MATH  Google Scholar 

  45. Rao, Y.V.K.S., Nakra, B.C.: Vibrations of unsymmetrical sandwich beams and plates with viscoelastic cores. J. Sound Vib. 34, 309–326 (1974)

    MATH  Google Scholar 

  46. Simon, J.: Compact sets in the space \(L^p(0, T;B)\). Ann. Mat. 146, 65–96 (1986)

    MATH  Google Scholar 

  47. Temam, R.: Infinite-Dimensional Dynamical Systems in Mechanics and Physics. Applied Mathematical Sciences, vol. 68. Springer, New York (1988)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Southwestern University of Finance and Economics, Chengdu, 611130, People’s Republic of China

    Baowei Feng

  2. Department of Mathematics, Western Kentucky University, Bowling Green, KY, 42101, USA

    Ahmet Özkan Özer

Authors
  1. Baowei Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmet Özkan Özer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmet Özkan Özer.

Ethics declarations

Conflict of interest

The authors have not disclosed any conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The financial support of the National Science Foundation of USA under Cooperative Agreement No. 1849213 is acknowledged by A. Ö. Özer.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Feng, B., Özer, A.Ö. Long-Time Behavior of a Nonlinearly-Damped Three-Layer Rao–Nakra Sandwich Beam. Appl Math Optim 87, 19 (2023). https://doi.org/10.1007/s00245-022-09931-7

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00245-022-09931-7

Keywords

Mathematics Subject Classification

Search

Navigation