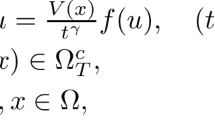Abstract
We consider the initial value problem (IVP) associated to a coupled system of Kawahara/KdV type equations. We prove the well-posedness results for given data in a Gevrey spaces. The proof relies on estimates in space-time norms adapted to the linear part of the equations. In particular, estimates in Bourgain spaces are proven for the linear and nonlinear terms of the system and the main result is obtained by a contraction principle. The class of system in view contains a number of systems arising in the modeling of waves in fluids, stability and instability of solitary waves and models for wave propagation in physical systems where both nonlinear and dispersive effects are important. The techniques presented in this work were based in Grujić and Kalisch, who studied the Gevrey regularity for a class of water-wave models and the well-posedness of a IVP associated to a general equation, whose the initial data belongs to Gevrey spaces.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Alarcon, E., Angulo, J., Montenegro, J.F.: Stability and instability of solitary waves for a nonlinear dispersive system. Nonlinear Anal. 36, 1015–1035 (1999)
Benedek, A., Panzone, R.: The spaces \(L^p\), with mixed norm. Duke Math. J. 28(3), 301–324 (1961)
Bona, J.L., Cohen, J., Wang, G.: Global well-posedness for a system of KDV-type equations with coupled quadratic nonlinearities. Nagoya Math. J. 215, 67–149 (2014)
Bourgain, J.: Fourier Transform Restriction Phenomena for Certain Lattice Subsets and Applications to Nonlinear Evolution Equations I. Geometric and Functional Analysis, Schröndiger Equations, pp. 107–156 (1993)
Bourgain, J.: Fourier Transform Restriction Phenomena for Certain Lattice Subsets and Applications to Nonlinear Evolution Equations II. Geometric and Functional Analysis, The KdV-Equation, pp. 209–262 (1993)
Carvajal, X., Panthee, M.: Sharp well-posedness for a coupled system of mKdV type equations. J. Evol. Equ. 19, 1167–1197 (2019)
Evans, L.C.: Partial Differential Equations, 2nd edn. American Mathematical Society, Providence (1998)
Gear, J., Grimshaw, R.: Weak and strong interactions between internal solitary waves equation. Stud. Appl. Math. 70, 235–258 (1984)
Grujić, Z., Kalisch, H.: Gevrey regularity for a class of water-wave models. Nonlinear Anal. 71, 1160–1170 (2009)
Ginibre, J., Tsutsumi, Y., Velo, G.: On the Cauchy problem for the Zakharov system. J. Funct. Anal. 151(2), 384–436 (1997)
Kawahara, T.: Oscillatory solitary waves in dispersive media. J. Phys. Soc. Jpn. 33, 260–264 (1972)
Kenig, C.E., Ponce, G., Vega, L.: The Cauchy problem for the Korteweg-de Vries equation in Sobolev spaces of negative indices. Duke Math. J. 71(1), 1–21 (1993)
Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 39, 422–443 (1895)
Linares, F., Ponce, G.: Introduction to Nonlinear Dispersive Equations, 2nd edn. Springer, New York (2015)
Acknowledgements
The second author was supported by the Coordenação de Aperfeiçoamento de Pessoal de nível Superior - Brasil (CAPES) - Finance Code 001. The authors express their thanks to Professor Henrik Kalisch, from Bergen University, for his valuable advices.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Kondo, C.I., Pes, R.B. Well-Posedness for a Coupled System of Kawahara/KdV Type Equations. Appl Math Optim 84, 2985–3024 (2021). https://doi.org/10.1007/s00245-020-09737-5
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00245-020-09737-5
Keywords
- Kawahara/KdV system
- Higher dispersion
- Well-posedness
- Bourgain spaces
- Analytic Gevrey spaces
- Multilinear estimates