Gröbner basis and the automaton property of Hecke–Kiselman algebras

Abstract

It is shown that the Hecke–Kiselman algebra associated to a finite directed graph is an automaton algebra in the sense of Ufnarovskii. Consequently, its Gelfand–Kirillov dimension is an integer if it is finite. Moreover, it is proved that the Hecke–Kiselman algebra associated to an oriented cycle admits a finite Gröbner basis.

1 Introduction

In the paper [7] of Ganyushkin and Mazorchuk a finitely generated monoid ${{\,\mathrm{HK}\,}}_{\Theta }$ was defined for an arbitrary finite simple digraph $\Theta$ with n vertices $\{1, \ldots , n\}$ by specifying generators and relations.

• (i) ${{\,\mathrm{HK}\,}}_{\Theta }$ is generated by idempotents $x_i^2 = x_i$, where $1 \le i \le n$,

• (ii) if the vertices i, j are not connected in $\Theta$, then $x_ix_j = x_jx_i$,

• (iii) if i, j are connected by an arrow $i \rightarrow j$ in $\Theta$, then $x_ix_jx_i = x_jx_ix_j = x_ix_j$,

• (iv) if i, j are connected by an (unoriented) edge in $\Theta$, then $x_ix_jx_i = x_jx_ix_j$.

If the graph $\Theta$ is unoriented (has no arrows), the monoid ${{\,\mathrm{HK}\,}}_{\Theta }$ is isomorphic to the so-called 0-Hecke monoid ${{\,\mathrm{H}\,}}_0(W)$, where W is the Coxeter group of the graph $\Theta$, see [6]. The latter monoid plays an important role in representation theory. In the case $\Theta$ is oriented (all edges are arrows) and acyclic, the monoid ${{\,\mathrm{HK}\,}}_{\Theta }$ is finite and it is a homomorphic image of the so-called Kiselman monoid $K_n$, see [7, 9]. It is worth mentioning that a characterization of general finite digraphs $\Theta$ such that the monoid ${{\,\mathrm{HK}\,}}_{\Theta }$ is finite remains an open problem, see [1].

The aim of this paper is to continue the study of the semigroup algebra $A = k[{{\,\mathrm{HK}\,}}_{\Theta }]$ over a field k, in the case when $\Theta$ is an oriented graph, that was started in [10], where it was shown that the growth of A is either polynomial or the monoid ${{\,\mathrm{HK}\,}}_{\Theta }$ contains a noncommutative free submonoid. The main result of the present paper states that the algebra A is automaton in the sense of Ufnarovskii [16], which means that the set of normal words of A forms a regular language. In other words, the set of normal words of A is determined by a finite automaton.

Theorem 1.1

Assume that $\Theta$ is a finite simple oriented graph. Then $A = k[{{\,\mathrm{HK}\,}}_{\Theta }]$ is an automaton algebra, with respect to any deg-lex order on the underlying free monoid of rank n. Consequently, the Gelfand–Kirillov dimension ${{\,\mathrm{GKdim}\,}}(A)$ of A is an integer if it is finite.

In the case when the digraph $\Theta$ is unoriented, the corresponding monoid algebra is known to be automaton. Indeed, as mentioned above: in this case ${{\,\mathrm{HK}\,}}_{\Theta } = {{\,\mathrm{H}\,}}_0(W)$, where W is the Coxeter group of the graph $\Theta$. In fact, one can prove that the reduced words for W and ${{\,\mathrm{H}\,}}_0(W)$ are the same, and two words represent the same element of the Coxeter group if and only if they represent the same element of the Coxeter monoid, see [14]. However, the set of normal forms of elements of a Coxeter group is known to be regular, see [4].

We note that it was proved in [10] that the following conditions are equivalent: 1) $k[{{\,\mathrm{HK}\,}}_{\Theta }]$ is a PI-algebra, 2) ${{\,\mathrm{HK}\,}}_{\Theta }$ does not contain a noncommutative free submonoid, 3) ${{\,\mathrm{GKdim}\,}}( k[{{\,\mathrm{HK}\,}}_{\Theta }])$ is finite, 4) $\Theta$ does not contain two different oriented cycles connected by an oriented path. Theorem 1.1 answers a question raised in [10].

The key method used to obtain this result is the description of a Gröbner basis of Hecke–Kiselman algebras. It is known that if the leading terms of the elements of this basis form a regular subset of the corresponding free monoid, then the algebra is automaton, see [16], Theorem 2 on p. 97. Consequently, our methods involve the monoid ${{\,\mathrm{HK}\,}}_{\Theta }$ only, rather than certain ring theoretical aspects of the algebra $k[{{\,\mathrm{HK}\,}}_{\Theta }]$. The obtained Gröbner basis is crucial for the approach to the structure of such algebras, which will be pursued in a forthcoming paper.

The class of automaton algebras was introduced by Ufnarovskii in [15]. The main motivation was to study a class of finitely generated algebras that generalizes the class of algebras that admit a finite Gröbner basis with respect to some choice of generators and an ordering on monomials. The difficulty here lies in the fact that there are infinitely many generating sets as well as infinitely many admissible orderings on monomials to deal with. There are examples of algebras with finite Gröbner bases with respect to one ordering, and infinite bases with respect to the other. Up until recently it was not known whether for any of known examples of automaton algebras with infinite Gröbner bases with respect to certain orderings one could find a better ordering that would yield a finite Gröbner basis. First counterexamples were found by Iyudu and Shkarin in [8].

There are many results indicating that the class of automaton algebras not only has better computational properties but also several structural properties that are better than in the class of arbitrary finitely generated algebras. For example, in this context one can refer to results on the Gelfand–Kirillov dimension, results on the radical in the case of monomial automaton algebras [15], results on prime algebras of this type [2], and also structural results concerned with the special case of finitely presented monomial algebras [11]. In particular, finitely generated algebras of the following types are automaton: commutative algebras, algebras defined by not more than two quadratic relations, algebras for which all the defining relations have the form $[x_ix_j] = 0$, for some pairs of generators, see [16]. Moreover, algebras that are finite modules over commutative finitely generated subalgebras are also of this type [5]. Several aspects of automaton algebras have been recently studied also in [8, 12, 13].

In Sect. 2 we introduce the necessary definitions and auxiliary results. Next, in Sect. 3, we determine a Gröbner basis of $k[{{\,\mathrm{HK}\,}}_{\Theta }]$, from which the main result follows. Finally, in Sect. 4, we prove that in the case when the graph $\Theta$ is a cycle, $k[{{\,\mathrm{HK}\,}}_{\Theta }]$ has a finite Gröbner basis. An example is given to show that this is not true for arbitrary Hecke–Kiselman algebras of oriented graphs, even in the case when the algebra satisfies a polynomial identity.

2 Definitions and the necessary background

Let F denote the free monoid on the set X of $n\ge 3$ free generators $x_1,\cdots ,x_n$. Let k be a field and let $k[F] =k\langle x_1,\cdots ,x_n\rangle$ denote the corresponding free algebra over k. Assume that a well order < is fixed on X and consider the induced degree-lexicographical order on F (also denoted by <). Let A be a finitely generated algebra over k with a set of generators $r_1, \ldots , r_n$ and let $\pi : k[F] \rightarrow A$ be the natural homomorphism of k-algebras with $\pi (x_i) = r_i$. We will assume that $\ker (\pi )$ is spanned by elements of the form $w-v$, where $w,v\in F$ (in other words, A is a semigroup algebra). Let I be the ideal of F consisting of all leading monomials of $\ker (\pi )$. The set of normal words corresponding to the chosen presentation for A and to the chosen order on F is defined by $N(A) = F \setminus I$. One says that A is an automaton algebra if N(A) is a regular language. That means that this set is obtained from a finite subset of F by applying a finite sequence of operations of union, multiplication and operation $*$ defined by $T^* = \bigcup _{i \ge 1}T^i$, for $T \subseteq F$. If $T = \{w\}$ for some $w \in F$, then we write $T^* = w^*$.

For every $x \in X$ and $w \in F$ by $|w|_x$ we mean the number of occurrences of x in w. By |w| we denote the length of the word w. The support of the word w, denoted by ${{\,\mathrm{supp}\,}}(w)$, stands for the set of all $x \in X$ such that $|w|_x > 0$. We say that the word $w = x_1\cdots x_r \in F$ is a subword of the word $v \in F$, where $x_i \in X$, if $v = v_1x_1\cdots v_r x_r v_{r+1}$, for some $v_1, \ldots , v_{r+1} \in F$. If $v_2, \ldots , v_r$ are trivial words, then we say that w is a factor of v.

Describing the normal words of a finitely generated algebra A is related to finding a Gröbner basis of the ideal $J=\ker (\pi )$. Recall that a subset G of J is called a Gröbner basis of J (or of A) if $0\notin G$, J is generated by G as an ideal and for every nonzero $f\in J$ there exists $g\in G$ such that the leading monomial ${\overline{g}}\in F$ of g is a factor of the leading monomial ${\overline{f}}$ of f. If G is a Gröbner basis of A, then a word $w\in F$ is normal if and only if w has no factors that are leading monomials in $g\in G$.

The so-called diamond lemma is often used in this context. We will follow the approach and terminology of [3]. By a reduction in k[F] determined by a pair $(w,w')\in F^2$, where $w' < w$ (the deg-lex order of F), we mean any operation of replacing a factor w in a word $f \in F$ by the factor $w'$. For a set $T \subseteq F^2$ of such pairs (these pairs will be called reductions as well) we say that the word $f \in F$ is T-reduced if no factor of f is the leading term w of a reduction $(w, w')$ from the set T. The deg-lex order on F satisfies the descending chain condition, which means there is no infinite decreasing chain of elements in F. This means that a T-reduced form of a word $w \in F$ can always be obtained in a finite series of steps. The linear space spanned by T-reduced monomials in k[F] is denoted by R(T).

The diamond lemma gives necessary and sufficient conditions for the set N(A) of normal words to coincide with the set of T-reduced words in F. The key tool is the notion of ambiguity. Let $\sigma = (w_{\sigma }, v_{\sigma })$, $\tau = (w_{\tau }, v_{\tau })$ be reductions in T. By an overlap ambiguity we mean a quintuple $(\sigma , \tau , l, w, r)$, where $1 \ne l, w, r \in F$ are such that $w_{\sigma } = wr$ and $w_{\tau } = lw$. A quintuple $(\sigma , \tau , l, w, r)$ is called an inclusive ambiguity if $w_{\sigma } = w$ and $w_{\tau } = lwr$. For brevity we will denote these ambiguities as $l(wr) = (lw)r$ and $l(w)r = (lwr)$, respectively. We will also say that they are of type $\sigma$-$\tau$. We say that the overlap (inclusive, respectively) ambiguity is resolvable if $v_{\tau }r$ and $lv_{\sigma }$ ($v_{\tau }$ and $lv_{\sigma }r$, respectively) have equal T-reduced forms. We use the following simplified version of Bergman’s diamond lemma.

Lemma 2.1

Let T be a reduction set in the free algebra k[F] over a field k, with a fixed deg-lex order in the free monoid F over X. Then the following conditions are equivalent:

• all ambiguities on T are resolvable,

• each monomial $f \in F$ can be uniquely T-reduced,

• if I(T) denotes the ideal of k[F] generated by $\{ w - v: (w, v) \in T \}$ then $k[F]=I(T) \oplus R(T)$ as vector spaces.

Moreover if the conditions above are satisfied then the k-algebra $A = k[F]/I(T)$ can be identified with R(T) equipped with a k-algebra structure with $f \cdot g$ defined as the T-reduced form of fg, for $f,g\in R(T)$. In this case, $\{ w - v: (w, v) \in T \}$ is a Gröbner basis of A.

3 Gröbner basis in the oriented graphs case

In this section we will prove that for any oriented graph $\Theta = (V(\Theta ), E(\Theta ))$, the language of normal words of the Hecke–Kiselman algebra $k[{{\,\mathrm{HK}\,}}_{\Theta }]$ is regular, and thus that the algebra is always automaton.

For $t \in V(\Theta )$ and $w \in F = \langle V(\Theta )\rangle$ we write $w \nrightarrow t$ if $|w|_t = 0$ and there are no $x \in {{\,\mathrm{supp}\,}}(w)$ such that $x \rightarrow t$ in $\Theta$. Similarly, we define $t \nrightarrow w$: again we assume that $|w|_t = 0$ and there is no arrow $t \rightarrow y$, where $y \in {{\,\mathrm{supp}\,}}(w)$. In the case when $t \nrightarrow w$ and $w \nrightarrow t$, we write $t \nleftrightarrow w$.

Theorem 3.1

Let $\Theta$ be a finite simple oriented graph with vertices $V(\Theta ) = \{x_1, x_2, \ldots , x_n\}$. Extend the natural ordering $x_1< x_2< \cdots < x_n$ on the set $V(\Theta )$ to the deg-lex order on the free monoid $F = \langle V(\Theta ) \rangle$. Consider the following set T of reductions on the algebra k[F]:

• (i) (twt, tw), for any $t \in V(\Theta )$ and $w \in F$ such that $w \nrightarrow t$,

• (ii) (twt, wt), for any $t \in V(\Theta )$ and $w \in F$ such that $t \nrightarrow w$,

• (iii) $(t_1wt_2, t_2t_1w)$, for any $t_1, t_2 \in V(\Theta )$ and $w \in F$ such that $t_1 > t_2$ and $t_2 \nleftrightarrow t_1w$.

Then the set $\{w - v, \text { where } (w, v) \in T\}$ forms a Gröbner basis of the algebra $k[{{\,\mathrm{HK}\,}}_{\Theta }]$.

Proof

Clearly, $w>v$ for every pair $(w,v)\in T$. Moreover, it is easy to see that w and v represent the same element of ${{\,\mathrm{HK}\,}}_{\Theta }$. It remains to use the diamond lemma. We will prove that all overlap and inclusive ambiguities of the reduction system T are resolvable. We begin with a simple observation. $\square$

Observation 3.2

Assume that $t \in V(\Theta )$ and $w \in F$ are such that $t \nleftrightarrow w$. Then the words tw and wt have equal T-reduced forms.

Proof

We argue by induction on the length |w| of w. If $w = 1$, the assertion is clear. If $w \in V(\Theta )$, then we either have $tw \xrightarrow {(iii)} wt$ or $wt \xrightarrow {(iii)} tw$, since $t \nleftrightarrow w$. We proceed with the induction step. Assume that $w = y_1 \cdots y_k$, where $y_i \in V(\Theta )$, for $i = 1, \ldots , k$. If $y_1 > t$, then we apply (iii) to wt and we are done. If there exists $i > 1$ such that $y_i > t$, then $y_1\cdots y_kt \xrightarrow {(iii)} y_1\cdots y_{i-1}ty_{i}\cdots y_k$. Now we apply the induction hypothesis to the words $ty_1\cdots y_{i-1}$ and $y_1\cdots y_{i-1}t$ and T-reduce them to some $w' \in F$. Thus we get that tw and wt can be both T-reduced to $w'y_{i}\cdots y_k$. Finally, if $y_i < t$, for all i, then by using reduction (iii) k times we get:

$$\begin{aligned} ty_1\cdots y_k \xrightarrow {(iii)} y_1ty_2 \cdots y_k \xrightarrow {(iii)} y_1y_2ty_3\cdots y_k \xrightarrow {(iii)} \cdots \xrightarrow {(iii)} y_1\cdots y_kt. \end{aligned}$$

$\square$

We will now list overlap and inclusive ambiguities of all possible types (x)–(y) of pairs of reductions in T, where (x), (y) $\in \{$(i), (ii), (iii)$\}$.

There are two overlap and one inclusive ambiguity of type (i)–(i):

• 1. $tw_1(tw_2t) = (tw_1t)w_2t$, for $t \in V(\Theta )$ and $w_1, w_2 \in F$ such that $w_1w_2 \nrightarrow t$,

• 2. $t_1w_1(t_2w_2t_1w_3t_2) = (t_1w_1t_2w_2t_1)w_3t_2$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $w_1t_2w_2 \nrightarrow t_1$ and $w_2t_1w_3 \nrightarrow t_2$,

• 3. $(t_1w_1t_2w_2t_2w_3t_1) = t_1w_1(t_2w_2t_2)w_3t_1$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $w_1t_2w_2t_2w_3 \nrightarrow t_1$ and $w_2 \nrightarrow t_2$.

There are two overlap and one inclusive ambiguity of type (i)–(ii):

• 4. $tw_1(tw_2t) = (tw_1t)w_2t$, for $t \in V(\Theta )$, $w_1, w_2 \in F$ such that $t \nrightarrow w_1$, $w_2 \nrightarrow t$,

• 5. $t_1w_1(t_2w_2t_1w_3t_2) = (t_1w_1t_2w_2t_1)w_3t_2$, for $t_1, t_2 \in V(\Theta )$ and $w_1, w_2, w_3 \in F$ such that $w_2t_1w_3 \nrightarrow t_2$, $t_1 \nrightarrow w_1t_2w_2$,

• 6. $(t_1w_1t_2w_2t_2w_3t_1) = t_1w_1(t_2w_2t_2)w_3t_1$, for $t_1, t_2 \in V(\Theta )$ and $w_1, w_2, w_3 \in F$ such that $w_1t_2w_2t_2w_3 \nrightarrow t_1$ and $t_2 \nrightarrow w_2$.

There are two overlap and three inclusive ambiguities of type (i)–(iii):

• 7. $t_1w_1(t_2w_2t_2) = (t_1w_1t_2)w_2t_2$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2$, $w_2 \nrightarrow t_2$ and $t_2 \nleftrightarrow t_1w_1$,

• 8. $t_1w_1(t_2w_2t_3w_3t_2) = (t_1w_1t_2w_2t_3)w_3t_2$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_1 > t_3,$$w_2t_3w_3 \nrightarrow t_2$ and $t_3 \nleftrightarrow t_1w_1t_2w_2$,

• 9. $(t_1w_1t_2w_2t_1) = (t_1w_1t_2)w_2t_1$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2$, $w_1t_2w_2 \nrightarrow t_1$ and $t_2 \nleftrightarrow t_1w_1$,

• 10. $(t_1w_1t_2w_2t_3w_3t_1) = t_1w_1(t_2w_2t_3)w_3t_1$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_2 > t_3,$$w_1t_2w_2t_3w_3 \nrightarrow t_1$ and $t_3 \nleftrightarrow t_2w_2$,

• 11. $(t_1w_1t_2w_2t_1) = t_1w_1(t_2w_2t_1)$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_2 > t_1$, $w_1t_2w_2 \nrightarrow t_1$ and $t_1 \nleftrightarrow t_2w_2$.

There are two overlap and one inclusive ambiguity of type (ii)–(i):

• 12. $tw_1(tw_2t) = (tw_1t)w_2t$, for $t \in V(\Theta )$, $w_1, w_2 \in F$ such that $w_1 \not \rightarrow t$, $t \nrightarrow w_2$,

• 13. $t_1w_1(t_2w_2t_1w_3t_2) = (t_1w_1t_2w_2t_1)w_3t_2$, for $t_1, t_2 \in V(\Theta )$ and $w_1, w_2, w_3 \in F$ such that $t_2 \nrightarrow w_2t_1w_3$, $w_1t_2w_2 \nrightarrow t_1$,

• 14. $(t_1w_1t_2w_2t_2w_3t_1) = t_1w_1(t_2w_2t_2)w_3t_1$, for $t_1, t_2 \in V(\Theta )$ and $w_1, w_2, w_3 \in F$ such that $t_1 \nrightarrow w_1t_2w_2t_2w_3$ and $w_2 \nrightarrow t_2$.

There are two overlap and one inclusive ambiguity of type (ii)–(ii):

• 15. $tw_1(tw_2t) = (tw_1t)w_2t$, for $t \in V(\Theta )$ and $w_1, w_2 \in F$ such that $t \nrightarrow w_1w_2$,

• 16. $t_1w_1(t_2w_2t_1w_3t_2) = (t_1w_1t_2w_2t_1)w_3t_2$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_1 \nrightarrow w_1t_2w_2$ and $t_2 \nrightarrow w_2t_1w_3$,

• 17. $(t_1w_1t_2w_2t_2w_3t_1) = t_1w_1(t_2w_2t_2)w_3t_1$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_1 \nrightarrow w_1t_2w_2t_2w_3$ and $t_2 \nrightarrow w_2$.

There are two overlap and three inclusive ambiguities of type (ii)–(iii):

• 18. $t_1w_1(t_2w_2t_2) = (t_1w_1t_2)w_2t_2$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2,$$t_2 \nrightarrow w_2$ and $t_2 \nleftrightarrow t_1w_1$,

• 19. $t_1w_1(t_2w_2t_3w_3t_2) = (t_1w_1t_2w_2t_3)w_3t_2$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_1 > t_3$, $t_2 \nrightarrow w_2t_2w_3$ and $t_3 \nleftrightarrow t_1w_1t_2w_2$,

• 20. $(t_1w_1t_2w_2t_1) = (t_1w_1t_2)w_2t_1$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2$, $t_1 \nrightarrow w_1t_2w_2$ and $t_2 \nleftrightarrow t_1w_1$,

• 21. $(t_1w_1t_2w_2t_3w_3t_1) = t_1w_1(t_2w_2t_3)w_3t_1$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_2 > t_3,$$t_1 \nrightarrow w_1t_2w_2t_3w_3$ and $t_3 \nleftrightarrow t_2w_2$,

• 22. $(t_1w_1t_2w_2t_1) = t_1w_1(t_2w_2t_1)$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_2 > t_1$, $t_1 \nrightarrow w_1t_2w_2$ and $t_1 \nleftrightarrow t_2w_2$.

There are two overlap and two inclusive ambiguities of type (iii)–(i):

• 23. $t_1w_1(t_1w_2t_2) = (t_1w_1t_1)w_2t_2$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2,$$w_1 \nrightarrow t_1$ and $t_2 \nleftrightarrow t_1w_2$,

• 24. $t_1w_1(t_2w_2t_1w_3t_3) = (t_1w_1t_2w_2t_1)w_3t_3$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_2 > t_3,$$w_1t_2w_2 \nrightarrow t_1$ and $t_3 \nleftrightarrow t_2w_2t_1w_3$,

• 25. $(t_1w_1t_1w_2t_2) = (t_1w_1t_1)w_2t_2,$ for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2$, $w_1 \nrightarrow t_1$ and $t_2 \nleftrightarrow t_1w_1t_1w_2$,

• 26. $(t_1w_1t_2w_2t_2w_3t_3) = t_1w_1(t_2w_2t_2)w_3t_3$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_1 > t_3$, $w_2 \nrightarrow t_2$ and $t_3 \nleftrightarrow t_1w_1t_2w_2t_2w_3$.

There are two overlap and two inclusive ambiguities of type (iii)–(ii):

• 27. $t_1w_1(t_1w_2t_2) = (t_1w_1t_1)w_2t_2$, for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2,$$t_1 \nrightarrow w_1$, $t_2 \nleftrightarrow t_1w_2$,

• 28. $t_1w_1(t_2w_2t_1w_3t_3) = (t_1w_1t_2w_2t_1)w_3t_3$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_2 > t_3$, $t_1 \nrightarrow w_1t_2w_2$ and $t_3 \nleftrightarrow t_2w_2t_1w_3$,

• 29. $(t_1w_1t_1w_2t_2) = (t_1w_1t_1)w_2t_2,$ for $t_1, t_2 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2$, $t_1 \nrightarrow w_1$ and $t_2 \nleftrightarrow t_1w_1t_1w_2$,

• 30. $(t_1w_1t_2w_2t_2w_3t_3) = t_1w_1(t_2w_2t_2)w_3t_3$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_1 > t_3$, $t_2 \nrightarrow w_2$ and $t_3 \nleftrightarrow t_1w_1t_2w_2t_2w_3$.

There are two overlap and three inclusive ambiguities of type (iii)–(iii):

• 31. $t_1w_1(t_2w_2t_3) = (t_1w_1t_2)w_2t_3$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2$, $t_2 > t_3$, $t_3 \nleftrightarrow t_2w_2$ and $t_2 \nleftrightarrow t_1w_1$,

• 32. $t_1w_1(t_2w_2t_3w_3t_4) = (t_1w_1t_2w_2t_3)w_3t_4$, for $t_1, t_2, t_3, t_4 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_1 > t_3,$$t_2 > t_4$, $t_4 \nleftrightarrow t_2w_2t_3w_3$ and $t_3 \nleftrightarrow t_1w_1t_2w_2$,

• 33. $(t_1w_1t_2w_2t_3) = (t_1w_1t_2)w_2t_3$, for $t_1, t_2, t_3 \in V(\Theta )$, $w_1, w_2 \in F$ such that $t_1 > t_2$, $t_1 > t_3$ and $t_3 \nleftrightarrow t_1w_1t_2w_2$, $t_2 \nleftrightarrow t_1w_1$,

• 34. $(t_1w_1t_2w_2t_3w_3t_4) = t_1w_1(t_2w_2t_3)w_3t_4$, for $t_1, t_2, t_3, t_4 \in V(\Theta )$, $w_1, w_2, w_3 \in F$ such that $t_1 > t_4$, $t_2 > t_3$, $t_4\nleftrightarrow t_1w_1t_2w_2t_3w_3$ and $t_3 \nleftrightarrow t_2w_2$,

• 35. $(t_1w_1t_2w_2t_3) = t_1w_1(t_2w_2t_3)$, for $t_1, t_2, t_3 \in V(\Theta )$. $w_1, w_2 \in F$ such that $t_1> t_3, t_2 > t_3$, $t_3 \nleftrightarrow t_1w_1t_2w_2$.

We will now solve these ambiguities.

• 1. $tw_1(tw_2t) \xrightarrow {(i)} tw_1tw_2 \xrightarrow {(i)} tw_1w_2$,

  $(tw_1t)w_2t \xrightarrow {(i)} tw_1w_2t \xrightarrow {(i)} tw_1w_2$.

• 2. $t_1w_1(t_2w_2t_1w_3t_2) \xrightarrow {(i)} t_1w_1t_2w_2t_1w_3 \xrightarrow {(i)} t_1w_1t_2w_2w_3,$

  $(t_1w_1t_2w_2t_1)w_3t_2 \xrightarrow {(i)} t_1w_1t_2w_2w_3t_2 \xrightarrow {(i)} t_1w_1t_2w_2w_3,$ since $w_2w_3 \nrightarrow t_2$.

• 3. $(t_1w_1t_2w_2t_2w_3t_1) \xrightarrow {(i)} t_1w_1t_2w_2t_2w_3 \xrightarrow {(i)} t_1w_1t_2w_2w_3$,

  $t_1w_1(t_2w_2t_2)w_3t_1 \xrightarrow {(i)} t_1w_1t_2w_2w_3t_1 \xrightarrow {(i)} t_1w_1t_2w_2w_3,$ since $w_1t_2w_2w_3 \nrightarrow t_1$.

• 4. $tw_1(tw_2t) \xrightarrow {(i)} tw_1tw_2 \xrightarrow {(ii)} w_1tw_2,$

  $(tw_1t)w_2t \xrightarrow {(ii)} w_1tw_2t \xrightarrow {(i)} w_1tw_2$.

• 5. $t_1w_1(t_2w_2t_1w_3t_2) \xrightarrow {(i)} t_1w_1t_2w_2t_1w_3 \xrightarrow {(ii)} w_1t_2w_2t_1w_3,$

  $(t_1w_1t_2w_2t_1)w_3t_2 \xrightarrow {(ii)}w_1t_2w_2t_1w_3t_2 \xrightarrow {(i)} w_1t_2w_2t_1w_3.$

• 6. $(t_1w_1t_2w_2t_2w_3t_1) \xrightarrow {(i)} t_1w_1t_2w_2t_2w_3 \xrightarrow {(ii)} t_1w_1w_2t_2w_3,$

  $t_1w_1(t_2w_2t_2)w_3t_1 \xrightarrow {(ii)}t_1w_1w_2t_2w_3t_1 \xrightarrow {(i)} t_1w_1w_2t_2w_3,$ since $w_1w_2t_2w_3 \nrightarrow t_1$.

• 7. $t_1w_1(t_2w_2t_2) \xrightarrow {(i)} t_1w_1t_2w_2 \xrightarrow {(iii)} t_2t_1w_1w_2$,

  $(t_1w_1t_2)w_2t_2 \xrightarrow {(iii)} t_2t_1w_1w_2t_2$. Since $t_2 \nleftrightarrow t_1w_1$, then $t_1w_1w_2 \nrightarrow t_2$ and we have:

  $t_2t_1w_1w_2t_2 \xrightarrow {(i)} t_2t_1w_1w_2.$

• 8. $t_1w_1(t_2w_2t_3w_3t_2) \xrightarrow {(i)} t_1w_1t_2w_2t_3w_3 \xrightarrow {(iii)} t_3t_1w_1t_2w_2w_3,$

  $(t_1w_1t_2w_2t_3)w_3t_2 \xrightarrow {(iii)} t_3t_1w_1t_2w_2w_3t_2 \xrightarrow {(i)} t_3t_1w_1t_2w_2w_3$, since $w_2w_3 \nrightarrow t_2$.

• 9. $(t_1w_1t_2w_2t_1) \xrightarrow {(i)} t_1w_1t_2w_2 \xrightarrow {(iii)} t_2t_1w_1w_2$,

  $(t_1w_1t_2)w_2t_1 \xrightarrow {(iii)} t_2t_1w_1w_2t_1 \xrightarrow {(i)} t_2t_1w_1w_2$, since $w_1w_2 \nrightarrow t_1$.

• 10. $(t_1w_1t_2w_2t_3w_3t_1) \xrightarrow {(i)} t_1w_1t_2w_2t_3w_3 \xrightarrow {(iii)} t_1w_1t_3t_2w_2w_3$,

  $t_1w_1(t_2w_2t_3)w_3t_1 \xrightarrow {(iii)} t_1w_1t_3t_2w_2w_3t_1 \xrightarrow {(i)} t_1w_1t_3t_2w_2w_3$, since $w_1t_3t_2w_2w_3 \nrightarrow t_1$.

• 11. $(t_1w_1t_2w_2t_1) \xrightarrow {(i)} t_1w_1t_2w_2$,

  $t_1w_1(t_2w_2t_1) \xrightarrow {(iii)} t_1w_1t_1t_2w_2 \xrightarrow {(i)} t_1w_1t_2w_2$, since $w_1 \nrightarrow t_1$.

• 12. $tw_1(tw_2t) \xrightarrow {(ii)} tw_1w_2t$,

  $(tw_1t)w_2t \xrightarrow {(i)} tw_1w_2t$.

• 13. $t_1w_1(t_2w_2t_1w_3t_2) \xrightarrow {(ii)} t_1w_1w_2t_1w_3t_2 \xrightarrow {(i)} t_1w_1w_2w_3t_2$, since $w_1w_2 \nrightarrow t_1$,

  $(t_1w_1t_2w_2t_1)w_3t_2 \xrightarrow {(i)} t_1w_1t_2w_2w_3t_2 \xrightarrow {(ii)} t_1w_1w_2w_3t_2$, since $t_2 \nrightarrow w_2w_3.$

• 14. $(t_1w_1t_2w_2t_2w_3t_1) \xrightarrow {(ii)} w_1t_2w_2t_2w_3t_1 \xrightarrow {(i)} w_1t_2w_2w_3t_1$,

  $t_1w_1(t_2w_2t_2)w_3t_1 \xrightarrow {(i)} t_1w_1t_2w_2w_3t_1 \xrightarrow {(ii)} w_1t_2w_2w_3t_1$, since $t_1 \nrightarrow w_1t_2w_2w_3$.

• 15. $tw_1(tw_2t) \xrightarrow {(ii)} tw_1w_2t \xrightarrow {(ii)} w_1w_2t$,

  $(tw_1t)w_2t \xrightarrow {(ii)} w_1tw_2t \xrightarrow {(ii)} w_1w_2t$.

• 16. $t_1w_1(t_2w_2t_1w_3t_2) \xrightarrow {(ii)} t_1w_1w_2t_1w_3t_2 \xrightarrow {(ii)} w_1w_2t_1w_3t_2$, since $t_1 \nrightarrow w_1w_2$,

  $(t_1w_1t_2w_2t_1)w_3t_2 \xrightarrow {(ii)} w_1t_2w_2t_1w_3t_2 \xrightarrow {(ii)} w_1w_2t_1w_3t_2$.

• 17. $(t_1w_1t_2w_2t_2w_3t_1) \xrightarrow {(ii)} w_1t_2w_2t_2w_3t_1 \xrightarrow {(ii)} w_1w_2t_2w_3t_1$,

  $t_1w_1(t_2w_2t_2)w_3t_1 \xrightarrow {(ii)} t_1w_1w_2t_2w_3t_1 \xrightarrow {(ii)} w_1w_2t_2w_3t_1$, since $t_1 \nrightarrow w_1w_2t_2w_3$.

• 18. $t_1w_1(t_2w_2t_2) \xrightarrow {(ii)} t_1w_1w_2t_2$,

  $(t_1w_1t_2)w_2t_2 \xrightarrow {(iii)} t_2t_1w_1w_2t_2$. Since $t_2 \nleftrightarrow t_1w_1$, we have $t_2 \nrightarrow t_1w_1w_2$ and thus:

  $t_2t_1w_1w_2t_2 \xrightarrow {(ii)} t_1w_1w_2t_2.$

• 19. $t_1w_1(t_2w_2t_3w_3t_2) \xrightarrow {(ii)} t_1w_1w_2t_3w_3t_2 \xrightarrow {(iii)} t_3t_1w_1w_2w_3t_2$, since $t_1 > t_3$ and $t_3 \nleftrightarrow t_1w_1w_2$,

  $(t_1w_1t_2w_2t_3)w_3t_2 \xrightarrow {(iii)} t_3t_1w_1t_2w_2w_3t_2 \xrightarrow {(ii)} t_3t_1w_1w_2w_3t_2$, since $t_2 \nrightarrow w_2w_3$.

• 20. $(t_1w_1t_2w_2t_1) \xrightarrow {(ii)} w_1t_2w_2t_1$,

  $(t_1w_1t_2)w_2t_1 \xrightarrow {(iii)} t_2t_1w_1w_2t_1 \xrightarrow {(ii)} t_2w_1w_2t_1$.

  Since $t_2 \nleftrightarrow w_1$, we can use Observation 3.2 to reduce $w_1t_2$ and $t_2w_1$ to the same form.

• 21. $(t_1w_1t_2w_2t_3w_3t_1) \xrightarrow {(ii)} w_1t_2w_2t_3w_3t_1 \xrightarrow {(iii)} w_1t_3t_2w_2w_3t_1$,

  $t_1w_1(t_2w_2t_3)w_3t_1 \xrightarrow {(iii)} t_1w_1t_3t_2w_2w_3t_1 \xrightarrow {(ii)} w_1t_3t_2w_2w_3t_1$.

• 22. $(t_1w_1t_2w_2t_1) \xrightarrow {(ii)} w_1t_2w_2t_1 \xrightarrow {(iii)} w_1t_1t_2w_2$,

  $t_1w_1(t_2w_2t_1) \xrightarrow {(iii)} t_1w_1t_1t_2w_2 \xrightarrow {(ii)} w_1t_1t_2w_2,$ since $t_1 \nrightarrow w_1$.

• 23. $t_1w_1(t_1w_2t_2) \xrightarrow {(iii)} t_1w_1t_2t_1w_2$. Since $t_2 \nleftrightarrow t_1w_2$, we have $w_1t_2 \nrightarrow t_1$ and:

  $t_1w_1t_2t_1w_2 \xrightarrow {(i)} t_1w_1t_2w_2$.

  $(t_1w_1t_1)w_2t_2 \xrightarrow {(i)} t_1w_1w_2t_2$. Since $t_2 \nleftrightarrow w_2$, then by Observation 3.2 we can reduce $t_2w_2$ and $w_2t_2$ to the same form.

• 24. $t_1w_1(t_2w_2t_1w_3t_3) \xrightarrow {(iii)} t_1w_1t_3t_2w_2t_1w_3$. Since $t_3 \nleftrightarrow t_2w_2t_1w_3$, then $w_1t_3t_2w_2 \nrightarrow t_1$ and:

  $t_1w_1t_3t_2w_2t_1w_3 \xrightarrow {(i)} t_1w_1t_3t_2w_2w_3$.

  $(t_1w_1t_2w_2t_1)w_3t_3 \xrightarrow {(i)} t_1w_1t_2w_2w_3t_3 \xrightarrow {(iii)} t_1w_1t_3t_2w_2w_3$, since $t_3 \nleftrightarrow t_2w_2w_3$ and $t_2 > t_3$.

• 25. $(t_1w_1t_1w_2t_2) \xrightarrow {(iii)} t_2t_1w_1t_1w_2 \xrightarrow {(i)} t_2t_1w_1w_2$,

  $(t_1w_1t_1)w_2t_2 \xrightarrow {(i)} t_1w_1w_2t_2 \xrightarrow {(iii)} t_2t_1w_1w_2$, since $t_1 > t_2$ and $t_2 \nleftrightarrow t_1w_1w_2$.

• 26. $(t_1w_1t_2w_2t_2w_3t_3) \xrightarrow {(iii)} t_3t_1w_1t_2w_2t_2w_3 \xrightarrow {(i)} t_3t_1w_1t_2w_2w_3$,

  $t_1w_1(t_2w_2t_2)w_3t_3 \xrightarrow {(i)} t_1w_1t_2w_2w_3t_3 \xrightarrow {(iii)} t_3t_1w_1t_2w_2w_3$, since $t_3 \nleftrightarrow t_1w_1t_2w_2w_3$ and $t_1 > t_3$.

• 27. $t_1w_1(t_1w_2t_2) \xrightarrow {(iii)} t_1w_1t_2t_1w_2$. Since $t_2 \nleftrightarrow w_2$, we have $t_1 \nrightarrow w_1t_2$, and thus:

  $t_1w_1t_2t_1w_2 \xrightarrow {(ii)} w_1t_2t_1w_2$.

  $(t_1w_1t_1)w_2t_2 \xrightarrow {(ii)} w_1t_1w_2t_2 \xrightarrow {(iii)} w_1t_2t_1w_2$.

• 28. $t_1w_1(t_2w_2t_1w_3t_3) \xrightarrow {(iii)} t_1w_1t_3t_2w_2t_1w_3$. Since $t_3 \nleftrightarrow t_2w_2t_1w_3$, we have $t_1 \nrightarrow w_1t_3t_2w_2$ and:

  $t_1w_1t_3t_2w_2t_1w_3 \xrightarrow {(ii)} w_1t_3t_2w_2t_1w_3.$

  $(t_1w_1t_2w_2t_1)w_3t_3 \xrightarrow {(ii)} w_1t_2w_2t_1w_3t_3 \xrightarrow {(iii)} w_1t_3t_2w_2t_1w_3$.

• 29. $(t_1w_1t_1w_2t_2) \xrightarrow {(iii)} t_2t_1w_1t_1w_2 \xrightarrow {(ii)} t_2w_1t_1w_2$,

  $(t_1w_1t_1)w_2t_2 \xrightarrow {(ii)} w_1t_1w_2t_2 \xrightarrow {(iii)} w_1t_2t_1w_2$, since $t_1 > t_2$ and $t_2 \nleftrightarrow t_1w_2$. Here, again we can see that $w_1 \nleftrightarrow t_2$ and thus $t_2w_1$ and $w_1t_2$ can be reduced to the same word, by Observation 3.2.

• 30. $(t_1w_1t_2w_2t_2w_3t_3) \xrightarrow {(iii)} t_3t_1w_1t_2w_2t_2w_3 \xrightarrow {(ii)} t_3t_1w_1w_2t_2w_3$,

  $t_1w_1(t_2w_2t_2)w_3t_3 \xrightarrow {(ii)} t_1w_1w_2t_2w_3t_3 \xrightarrow {(iii)} t_3t_1w_1w_2t_2w_3$, since $t_3 \nleftrightarrow t_1w_1w_2t_2w_3$ and $t_1 > t_3$.

• 31. $t_1w_1(t_2w_2t_3) \xrightarrow {(iii)} t_1w_1t_3t_2w_2 \xrightarrow {(iii)} t_2t_1w_1t_3w_2$, since $t_1 > t_2$ and $t_2 \nleftrightarrow t_1w_1t_3$,

  $(t_1w_1t_2)w_2t_3, \xrightarrow {(iii)} t_2t_1w_1w_2t_3$.

  Since $t_3 \nleftrightarrow w_2$ then by Observation 3.2$t_3w_2$ and $w_2t_3$ can be reduced to the same form.

• 32. $t_1w_1(t_2w_2t_3w_3t_4) \xrightarrow {(iii)} t_1w_1t_4t_2w_2t_3w_3 \xrightarrow {(iii)} t_3t_1w_1t_4t_2w_2w_3$, since $t_3 \nleftrightarrow t_1w_1t_4t_2w_2$ and $t_1 > t_3$,

  $(t_1w_1t_2w_2t_3)w_3t_4 \xrightarrow {(iii)} t_3t_1w_1t_2w_2w_3t_4 \xrightarrow {(iii)} t_3t_1w_1t_4t_2w_2w_3$, since $t_4 \nleftrightarrow t_2w_2w_3$ and $t_2 > t_4$.

• 33. $(t_1w_1t_2w_2t_3) \xrightarrow {(iii)} t_3t_1w_1t_2w_2 \xrightarrow {(iii)} t_3t_2t_1w_1w_2$, since $t_1 > t_2$ and $t_2 \nleftrightarrow t_1w_1$,

  $(t_1w_1t_2)w_2t_3 \xrightarrow {(iii)} t_2t_1w_1w_2t_3 \xrightarrow {(iii)} t_2t_3t_1w_1w_2$, since $t_1 > t_3$ and $t_3 \nleftrightarrow t_1w_1w_2$.

  Since $t_2 \nleftrightarrow t_3$, we either have $t_2t_3 \xrightarrow {(iii)} t_3t_2$, or $t_3t_2 \xrightarrow {(iii)} t_2t_3$.

• 34. $(t_1w_1t_2w_2t_3w_3t_4) \xrightarrow {(iii)} t_4t_1w_1t_2w_2t_3w_3 \xrightarrow {(iii)} t_4t_1w_1t_3t_2w_2w_3$,

  $t_1w_1(t_2w_2t_3)w_3t_4 \xrightarrow {(iii)} t_1w_1t_3t_2w_2w_3t_4 \xrightarrow {(iii)} t_4t_1w_1t_3t_2w_2w_3$, since $t_1 > t_4$ and $t_4 \nleftrightarrow t_1w_1t_3t_2w_2w_3$.

• 35. $(t_1w_1t_2w_2t_3) \xrightarrow {(iii)} t_3t_1w_1t_2w_2,$

  $t_1w_1(t_2w_2t_3) \xrightarrow {(iii)} t_1w_1t_3t_2w_2 \xrightarrow {(iii)} t_3t_1w_1t_2w_2$, since $t_1 > t_3$ and $t_3 \nleftrightarrow t_1w_1$.

We have checked that all ambiguities of the reduction system T are resolvable. Thus the diamond lemma can be applied and the result follows. $\square$

We are ready to prove our first main result.

Proof of Theorem 1.1

We have

$$\begin{aligned} N_{\Theta } = N_{(i)} \cup N_{(ii)} \cup N_{(iii)}, \end{aligned}$$

where $N_{\Theta }$ stands for the set of leading terms in pairs from the set T considered in Theorem 3.1, and $N_{(i)}, N_{(ii)}, N_{(iii)}$ are the sets of leading terms from the three families (i), (ii), (iii) of reductions in T, respectively. We only need to show that the sets $N_{(i)}, N_{(ii)}, N_{(iii)}$ are regular.

Indeed, observe that $N_{(i)} = \{tvt\, | \, t \in V(\Theta ), v \in F, v \nrightarrow t\} = \bigcup \limits _{t \in V(\Theta )}\{tvt \mid v \nrightarrow t\}$ which is a finite union of sets of the form $t\langle Y_t \rangle t$, where $Y_t$ is the subset of $V(\Theta )$ consisting of all generators z such that $z \nrightarrow t$. All these summands are clearly regular. Thus $N_{(i)}$ is regular. A similar argument works for $N_{(ii)}$.

Finally,

$$\begin{aligned} N_{(iii)} = \bigcup \limits _{x,z \in V(\Theta ), x<z, x\nleftrightarrow z} z\langle X_x\rangle x, \end{aligned}$$

where $X_x \subseteq V(\Theta )$ is the subset consisting of all generators $y \in V(\Theta )$ such that $y \nleftrightarrow x$. Again, these summands are clearly regular. Therefore, the set $N_{(iii)}$ is regular as a union of regular sets.

As a result, the entire set $N_{\Theta }$ is regular and it is well known that this implies that the algebra $k[{{\,\mathrm{HK}\,}}_{\Theta }]$ is automaton, see [16], p. 97. The fact that ${{\,\mathrm{GKdim}\,}}(k[{{\,\mathrm{HK}\,}}_{\Theta }])$ is an integer, if it is finite, follows, see [16], Theorem 3 on p. 97 and Theorem 1 on p. 90. $\square$

4 Gröbner basis of a cycle monoid

Let $C_n$ denote the Hecke–Kiselman monoid associated to the cycle consisting of $n\ge 3$ vertices. The aim of this section is to prove that in the case of $k[C_n]$ one can find a finite subset of the Gröbner basis obtained in the previous section such that it itself forms a Gröbner basis of $k[C_n]$. Our interest in this special case comes from the fact that the structure of the algebra $k[C_{n}]$ is crucial for the study of an arbitrary algebra $k[{{\,\mathrm{HK}\,}}_{\Theta }]$.

Recall that the monoid $C_n$ is defined by generators $x_1,\cdots ,x_n$ subject to the following relations:

$$\begin{aligned}&\displaystyle x_i^2=x_i,\\&\displaystyle x_ix_{i+1}x_i=x_{i+1}x_ix_{i+1}=x_ix_{i+1}, \end{aligned}$$

for all $i=1,\cdots ,n$ (with the convention that indices are taken modulo n) and

$$\begin{aligned} x_ix_j=x_jx_i \end{aligned}$$

for all $i,j=1,\cdots ,n$ satisfying $1<i-j<n-1$ (note that for $n=3$ there are no relations of this type).

The natural order $x_1< x_2< \cdots < x_n$ is considered on the set of generators and the corresponding deg-lex order on the free monoid F. We also adopt the following notation in this section. When we write a word of the form: $x_i \cdots x_j$, we mean that consecutive generators from $x_i$ up to $x_j$ if $i<j$ (or down to $x_{j}$, if $i > j$) appear in this word. For instance, $x_2 \cdots x_5$ denotes $x_2x_3x_4x_5$ and $x_6\cdots x_3$ stands for the word $x_6x_5x_4x_3$.

Consider two sets S and $S'$ of reductions on k[F]. The first one is a subset of the system T considered in the previous section that consists of all pairs of the form:

• (1) $(x_ix_i,x_i)$ for all $i\in \{1,\cdots ,n\}$,

• (2) $(x_jx_i,x_ix_j)$ for all $i,j\in \{1,\cdots ,n\}$ such that $1<j-i<n-1$,

• (3) $(x_n(x_1\cdots x_i)x_j,x_jx_n(x_1\cdots x_i))$ for all $i,j\in \{1,\cdots ,n\}$ such that $i+1<j<n-1$,

• (4) $(x_iux_i,x_iu)$ for all $i\in \{1,\cdots ,n\}$ and $1\ne u\in F$ such that $u \nrightarrow x_i$. Here, $i-1 = n$, for $i = 1$ (we say, for the sake of simplicity, that the word $x_iux_i$ is of type $(4x_i)$),

• (5) $(x_ivx_i,vx_i)$ for all $i\in \{1,\cdots ,n\}$ and $1\ne v\in F$ such that $x_i \nrightarrow u$. Here $i+1 = 1$, for $i =n$ (similarly, we say that the word $x_ivx_i$ is of type $(5x_i)$).

The second set of reductions is a subset $S'$ of S consisting of:

• (i) all pairs of type (1)–(3),

• (ii) all pairs $(x_iux_i,x_iu)$ of type (4) such that $|u|_{x_{j}}\le 1$, for $j\in \{1,\cdots ,n\}\setminus \{i,i-1\}$,

• (iii) all pairs $(x_ivx_i,vx_i)$ of type (5) such that $|v|_{x_{j}}\le 1$ for $j\in \{1,\cdots ,n\}\setminus \{i,i+1\}$,

• (iv) all pairs $(x_izx_i,zx_i)$ of type (5) such that $i < n$ and:

  $$\begin{aligned} x_izx_i = x_i(x_{i_1}\cdots x_{j_1})(x_{i_2}\cdots x_{j_2}) \cdots (x_{i_k} \cdots x_{j_k})x_n(x_1\cdots x_i), \end{aligned}$$

  where $i_1< i_2< \cdots< i_k < n$ and $j_1< j_2< \cdots< j_k < n$.

We will say that the word $x_iux_i$ that appears in (ii) is of type $(4x_{i}')$, the word $x_ivx_i$ that appears in (iii) is of type $(5x_{i}')$, and the word $x_izx_i$ that appears in (iv) is of type $(5x_{i}'')$. We will also say that a word $x \in F$ is of type (1), (2), or (3), respectively, if x is the leading term of one of the reductions of the corresponding type.

One can recognize reductions of type (1) and (4) as subsets of the reduction set (i) from Theorem 1.1. Similarly, reductions of types (2), (3) are special cases of reductions of type (iii) and reductions of type (5) correspond to the subset (ii) of T. It is convenient to explicitly distinguish five families of reductions of the system S, as they will be repeatedly used in the process of reducing the size of the Gröbner basis obtained in the previous section.

We will prove two facts concerning the reduction sets S and $S'$.

Lemma 4.1

Let T be a reduction set on $k[C_n]$ obtained in Sect. 2. If $w \in F$ is T-reduced, then it is also S-reduced.

Lemma 4.2

Every $S'$-reduced word in F is S-reduced.

The first lemma is a simple observation that is an intermediate step towards the main result of this section.

Proof of Lemma 4.1

Assume, to the contrary, that some word $w \in F$ is S-reduced, but not T-reduced. Clearly, it is enough to consider the case where w is of the form (iii) from the definition of T, namely $v = x_kwx_i$, where $k > i$ and $x_i \nleftrightarrow x_kw$. We will use inductive argument to show that v is not S-reduced, which leads to a contradiction.

Of course, if $|w| = 0$ then $x_kx_i \xrightarrow {(2)} x_ix_k$, so $x_kx_i$ is S-reducible. We proceed with the inductive step. Let $|w| > 0$ and let $w = x_{i_1}\cdots x_{i_r}$, for some $x_{i_s} \in \{x_1,\ldots , x_n \}$ such that $x_{i_s} \nleftrightarrow x_i$, for $1 \le s \le r$. If for any s we have $i_s > i$ then the factor $x_{i_s}\cdots x_{i_r}x_i$ is of the form (iii) and thus it is not S-reduced, by the induction hypothesis. So we only need to consider the case where $i_s \le i < k$, for all s. In particular, we have $i_1 \le i < k$. We consider two cases.

Case 1. $k = n$. Here we must have $i_1 = 1$. Otherwise, an S-reducible factor $x_nx_{i_1}$ appears in v and the induction step follows. If an S-reducible factor of the form (3) appears in v, then we are done, so we may only consider the case where $i_2 = 2, i_3 = 3, \ldots , x_r = r$. However, it follows that $r < i$, since $i_s < i$, for all s. Since $x_i \nleftrightarrow w = x_nx_1\cdots x_r$, we must have $i > r+1$, which means that v is of the form (3) and w is thus S-reducible. The induction step follows again.

Case 2. $k < n$. In this case we either have $i_1 < k-1$ and an S-reducible factor $x_kx_{i_1}$ appears in v, which yields the induction step, or $i_1 = k - 1$. In the latter case we have $v = x_kx_{k-1}x_{i_2} \cdots x_rx_i$. However now we can repeat the argument for $i_1$ to obtain that the only relevant case is $i_2 = k-2.$ Indeed, we have $i_2 \ne k-1$, $i_2 \ne k$ and $i_2 \le i < k$. If we were to assume that $i_2 < k-2$, then the S-reducible factor $x_{k-1}x_{i_2}$ would appear in v, which would immediately yield the inductive step. After repeating this process we are left with the case when $v x_i= x_kx_{k-1}x_{k-2} \cdots x_m \cdot x_i$. However, since $k > i$ and $x_i \nleftrightarrow x_kw$, we have $k > m-1$, so we get and an S-reducible factor $x_mx_i$. Thus, the induction step follows again.

We have shown that the word v of the form (iii) is S-reducible, which yields a contradiction. The assertion follows.

Before proving Lemma 4.2, we will prove the following fact concerning certain special family of words.

Observation 4.3

Assume that $1 \ne p \in F$ is such that $|p|_{x_{n}} = 0$ and p does not contain factors of the forms (1)-(3), $(4x_i')$, $(5{x_i}')$, where $1 \le i \le n$. Then there exists $k \in {\mathbb {N}}$ such that p is of the form:

$$\begin{aligned} (x_{i_1}\cdots x_{j_1})(x_{i_2}\cdots x_{j_2}) \cdots (x_{i_k} \cdots x_{j_k}), \end{aligned}$$

(4.1)

where $i_1< i_2< \cdots < i_k$ and $j_1< j_2< \cdots < j_k$, if $k > 1$.

Proof

We need some additional notation. We will say that a factor v of a word $w \in F$ is a block if v is of the form $x_{i}\cdots x_{j}$, for some $1 \le i,j < n$, but there is no factor $v'$ of w such that v is a factor of $v'$, the latter is also of the form $x_{i'}\cdots x_{j'}$, for some $1 \le i',j' < n$, and $v \ne v'$. The length of a block v is defined as the number $|j-i+1|$. The block is called increasing if $i \le j$ and decreasing if $i \ge j$ (note that $|p|_{x_{n}} = 0$).

Take $p \ne 1$ such that $|p|_{x_{n}} = 0$. Since p cannot have subwords of the form $x_j x_{j+1}x_{j}$ or $x_{j}x_{j-1}x_{j}$ (conditions $(4x_i')$, $(5{x_i}')$, respectively), it follows that p is (in a unique way) a product of blocks and, by definition, the product of two consecutive blocks is not a block. If p is a product of an exactly one block then there is nothing to prove – p is of the form (4.1). Assume that p is a product of at least two blocks and take two consecutive blocks of the form $(x_{i_s}\cdots x_{j_s})(x_{i_{s+1}}\cdots x_{j_{s+1}})$. Observe first, that we cannot have $i_{s+1} \le j_s +1$. Indeed, if $i_{s+1} <j_s - 1$, then a factor of type (2) would appear in p, a contradiction. If we had $i_{s+1} = j_s \pm 1$, then either the product of the two blocks $(x_{i_s}\cdots x_{j_s})(x_{i_{s+1}}\cdots x_{j_{s+1}})$ is a block itself, or a factor of one of the forms $x_{j_s}x_{j_{s}-1}x_{j_s}$, $x_{j_s}x_{j_{s}+1}x_{j_s}$ appears in p, again a contradiction. Of course, we cannot have $i_{s+1} = j_s$, as this yields a factor of type (1) in p.

We will prove that $i_s < i_{s+1}$. Note that we cannot have $i_s = i_{s+1}$ since this immediately gives a factor $x_{i_s}\cdots x_{j_s}x_{i_{s}}$ of type $(4x_{i_s}')$ or $(5x_{i_s}')$ in p, a contradiction. Assume, to the contrary, that $i_{s+1} < i_{s}$. We already know that must have $i_{s+1} > j_s +1$, so $j_s +1< i_{s+1} < i_{s}$ and thus the first block is decreasing of length $> 1$ and the factor of the form $x_{i_{s+1}} \cdots x_{j_s} x_{i_{s+1}}$ of type $(5x_{i_{s+1}}')$ appears in p, a contradiction. So $i_s < i_{s+1}$. The inequality $j_s < j_{s+1}$ is proved in a completely analogous way. $\square$

Proof of Lemma 4.2

Assume, to the contrary, that some word $w \in F$ is $S'$-reduced, but not S-reduced. We may choose w to be minimal with respect to the deg-lex order on F. It is clear that w may only be of the form $(4x_i)$ or $(5x_i)$.

We will first consider the case $(4x_i)$; in other words $w = x_iux_i$, for some $u \ne 1$, $|u|_{x_{i-1}} = |u|_{x_{i}} = 0$ (if $i = 1$, then $i-1 = n$).

First, observe that $i \ne n$. Indeed, if $i = n$, then as w is S’-reduced and $|u|_{x_{n}} = 0$, u is of the form (4.1) and

$$\begin{aligned} w = x_n(x_{i_1}\cdots x_{j_1})(x_{i_2}\cdots x_{j_2}) \cdots (x_{i_k} \cdots x_{j_k})x_n, \end{aligned}$$

(4.2)

for some k and $i_1< i_2< \cdots < i_k$ and $j_1< j_2< \cdots < j_k$, if $k > 1$. As $|w|_{x_{n-1}} = 0$ and $x_nx_{i_1}$ cannot be of the form (2), we have $i_1 = 1$ and the first block of u is increasing. If $k > 1$, however, then $i_2 > j_1 + 1$, since otherwise a factor $x_{i_2}\cdots x_{j_1}x_{i_2}$ of the form ($4x_{i_2}'$) appears in w, which is impossible. But if $i_2 \ne n-1$, then $x_nx_{i_1}\cdots x_{j_1}x_{i_2}$ is a factor of type (3) in w, a contradiction. Thus $k = 1$. In this case, however, $w = x_n(x_{1}\cdots x_{j_1})x_n$ is of the form $(4x_{n}')$, again a contradiction. Therefore $i \ne n$.

Let $t = \max \{l: |u|_{x_{l}} \ne 0\}$. Of course, $t > 1$ as otherwise w is $S'$-reducible. Moreover, $t > i$ since otherwise w has a prefix $x_ix_m$ with $m<i-1$, which is a word of the form (2), a contradiction. We consider two cases: $1< t <n$ and $t=n$.

• Case 1. $1< t < n$. Since w is $S'$-reduced and $|w|_{x_{n}} = 0$, then by Observation 4.3w is of the form (4.1), for some k and $i_1< \cdots < i_k$, $j_1< \cdots < j_k$, if $k > 1$. But since w is of the form $(4x_i)$, the first block of w must begin with $x_i$, and the last block must end with $x_i$. If the length of the first block $x_i \cdots x_{j_1}$ was greater than 1, then this block must have been increasing, since $|w|_{x_{i-1}} = 0$. However, in this case $i = i_1 < j_1 \le j_k = i$, which is impossible. Thus the first block of w consists just of $x_i$. If $k = 1$, then $w = x_i$, a contradiction. If $k > 1$, then $j_k > j_1$, which is impossible, as $i_1 = j_1 < j_k = i$. Again, a contradiction.

• Case 2. $t = n$. Then $i\ne 1$ because we are in the case $(4x_i)$. Consider the last appearance of $x_n$ in w, namely let $w = x_ipx_nqx_i$, where $p, q \in X$ and $|q|_{x_{n}} = 0$. First, assume that $q = 1$. Then i must be equal to $n-1$ since otherwise we would have a factor of type (2) in w. Hence $w = x_{n-1}px_nx_{n-1}$. If $p = 1$, then w is of type $(4x_{n-1}')$, which is impossible as w is $S'$-reduced. Thus $p = x_np'$, since otherwise w contains a factor $x_{n-1}x_s$ of type (2). Thus w has a proper factor $x_np''x_n$ of type $(4x_n)$, contradicting the minimality of the word w. Thus we may assume that $q \ne 1$. Since w is $S'$-reduced, also $qx_i$ is $S'$-reduced and since $|qx_i|_{x_{n}} = 0$, as $i < n$, we can apply Observation 4.3 and assume that it is of the form (4.1), for some k and $i_1< \cdots < i_k$ and $j_1< \cdots < j_k$, if $k > 1$. However, since $x_nx_{i_1}$ is a factor of w we must have $i_1 = n-1$ or $i_1 = 1$, as otherwise w has a factor of type (2). We consider these subcases now:

  • (a) If $i_1 = n-1$, then there is only one block in the decomposition (4.1) of $qx_i$, otherwise another block of $qx_i$ would have to begin with $x_{i_2}$, where $i_2 > i_1$ and also $n >i_2$. This is impossible. Therefore $w = x_ipx_nx_{n-1} \cdots x_i$. If $p = 1$ then w is the form $(4x_{i}')$, a contradiction. Assume that $p \ne 1$. Then $x_ipx_n\cdots x_{i+1}$ cannot contain two occurrences of $x_{i+1}$ as that would yield a factor of the form $(4x_{i+1})$ in w, which contradicts its minimality. Thus $|x_ipx_n\cdots x_{i+2}|_{x_{i+1}} = 0$ and we can see that $x_ipx_n\cdots x_{i+2}$ cannot contain two occurrences of $x_{i+2}$. Continuing this way, we can see that $|p|_{x_{l}} = 0$, for $n \ge l > i-1$. Thus $p = x_mp'$, for some $p'$, for some $m < i-1$ and thus we have a factor $x_ix_m$ of type (2) in w, a contradiction.

  • (b) If $i_1 = 1$, then $qx_i$ is of the form $(x_{1}\cdots x_{j_1}) \cdots (x_{i_k} \cdots x_i)$. We cannot have $k = 1$, since in that case, we would have a factor of the form $x_1\cdots x_i$ in w. Its length would be greater than 1, since $i \ne 1$. Therefore, w would contain $x_{i-1}$, a contradiction. If $k > 1$ then as in the case of words of the form (4.2) we have $i_2 = n-1$. This easily implies that $k = 2$ and $w = x_ipx_n(x_{1}\cdots x_{j_1})(x_{n-1} \cdots x_i)$. Next, if $p = 1$ then, since $1 \le j_1 < i - 1$ the word w is of the form $(4x_{i}')$, whence w is $S'$-reducible, a contradiction. Let $p \ne 1$. As in the previous subcase, we can easily see that $|p|_{x_{l}}=0$ for $l=i+1, \ldots , n-1$. Again, if $|p|_{x_{n}} \ne 0$, the minimality of w is violated, and thus $|p|_{x_{n}} = 0$. Therefore $p = x_mp'$, for some $m < i-1$. As in the previous case, a factor $x_ix_m$ of type (2) appears in w, a contradiction.

We have proved that if w is $S'$-reduced of the form $(4x_i)$, then it is also S-reduced. Assume now that w is a minimal $S'$-reduced word of the form $(5x_i)$ with respect to the deg-lex order on F. Namely, $w = x_iux_i$, for some $u \ne 1$, $|u|_{x_{i+1}} = |u|_{x_{i}} = 0$. Formally, we need to note that $i+1 = 1$, if $i = n$, but we will begin with showing that in fact $i \ne n$.

Assume the contrary, that $w = x_nux_n$ is of the form $(5x_n)$. Thus $|u|_{x_{n}} = 0$ and by Observation 4.3u must be of the form (4.1), for some k and $i_1, \ldots , i_k$, $j_1, \ldots , j_k$. Since $x_nx_{i_1}$ cannot be a factor of the form (2), and $i_1 \ne 1$, we must have $i_1 = n-1$. This implies, that u is a product of only one block $x_{n-1}\cdots x_{j_1}$. Since $j_1 > 1$ we can see that w is of the form $(5x_n')$, a contradiction. Thus $i < n$.

Our approach will be similar to that from the first part of the proof. Again, consider $t = \max \{l: |u|_{x_{l}} \ne 0\}$. Clearly, $t > 1$, as otherwise w is $S'$-reducible. The proof breaks into two cases:

• Case 1. $t < n$. Since w is $S'$-reduced and $|w|_{x_{n}} = 0$, it satisfies the conditions of Observation 4.3. Thus it must be of the form (4.1), namely $w = (x_{i_1}\cdots x_{j_1})(x_{i_2}\cdots x_{j_2}) \cdots (x_{i_k} \cdots x_{j_k}),$ where $i_1< i_2< \cdots < i_k$ and $j_1< j_2< \cdots < j_k$, if $k > 1$. Of course, w cannot consist of only one block $x_{i_1}\cdots x_{j_1}$, since otherwise we have $i_1 = j_1 = i$ and thus $w=x_{i}$, a contradiction. Hence $k > 1$. We claim that $j_l \ge i$, for all $l > 1$. Indeed, if we had $j_l < i$, for some $1 < l \le k$, then the block $x_{i_l}\cdots x_{j_l}$ would have to be decreasing, as $i_l > i_1 = i$, and thus it would contain $x_{i+1}$, a contradiction with the fact that w is of the form $(5x_i)$. Thus $j_l \ge i$, for all $l > 1$. Consider the second block $x_{i_2}\cdots x_{j_2}$ of w. Of course $i_2 > i_1 = i$. If we had $j_2 = i$, then the entire second block of w would be decreasing and it would contain $x_{i+1}$, a contradiction. So $j_2 > i$. It follows that $i = j_k \ge j_2 > i$, and we arrive at a contradiction, again.

• Case 2. $t= n$. Notice that $i\ne n-1$ in this case. We assume, again, that $w = x_ipx_nqx_i$, where $|q|_{x_{n}} = 0$. To avoid the appearance of a factor of type (2) in w, we must restrict ourselves to one of the following subcases: (a) $q = 1$, (b) $q = x_1q'$, or (c) $q = x_{n-1}q'$, where $q' \in F$.

  • Subcase (a). If $q = 1$, then $w = x_ipx_nx_i$. Therefore, $i = n-1$ or $i=1$, otherwise we have a factor of the form (2) in w. The first case was excluded in the beginning of Case 2. So $w = x_1px_nx_1$. Thus $p \ne 1$, as otherwise w is of type $(5x_1')$. Also, observe that $|p|_{x_{n}} = 0$, since otherwise we would have a proper factor $x_np'x_n$ of w such that $|p'|_{x_{n}} = |p'|_{x_{l}} = 0$ and thus this factor would be of the form $(5x_n)$. This violates the minimality of w as a minimal $S'$-reduced and S-reducible word with respect to the deg-lex order in F. This means that $x_1p$ satisfies the conditions of Observation 4.3 and is of the form (4.1), so that w is of the form $(5x_1'')$. This contradicts the fact that it is $S'$-reduced.

  • Subcase (b). $q = x_1q'$. Again, $qx_i$ is of the form (4.1) and as $i < n-1$ it follows, using the same arguments as in the case of words of the form (4.2), that $qx_i$ must be a single block and thus $w = x_ipx_nx_1\cdots x_i$. Now, by an argument used in the subcase (b) of Case 2 in the first part of the proof, when we considered words w of type $(4x_i)$, we can assume that $|p|_{x_{j}} =0$ for $j=i-1,i-2, \ldots ,1, n$. So $|p|_{x_{n}} = 0$ allows us to apply Observation 4.3 to prove that p is of the form (4.1). This yields a contradiction, as w is again proved to be of the form $(5x_i'')$.

  • Subcase (c). $q = x_{n-1}q'$. Once again, $qx_i$ is of the form (4.1). As the first block of $qx_i$ begins with $x_{n-1}$ we can see, as before, that this is in fact the only block of this word. Otherwise another block of $qx_i$ would have to begin with $x_{i_2}$, where $i_2 > i_1 = n-1$ and also $n >i_2$. This is impossible. Thus $qx_i = x_{n-1}q'x_i$ is a a single decreasing block of length greater than 1 which is impossible, as $|u|_{x_{i+1}} = 0$.

  The subcases (a)–(c) have been proved to lead to a contradiction. Therefore, also in the case when $t = n$ we can see that no w can be $S'$-reduced but S-reducible.

So, every $S'$-reduced word is S-reduced. Thus, Lemma 4.2 is proved.

It now follows easily from Lemma 4.1 that the reduction system S satisfies the diamond lemma, because the reduction system T satisfies this. And similarly, Lemma 4.2 implies then that the reduction system $S'$ satisfies the diamond lemma. Consequently, we have proved the following theorem.

Theorem 4.4

$G'=\{w-w':(w,w')\in S'\}\subseteq k[F]$ forms a finite Gröbner basis and $G=\{w-w':(w,w')\in S\}\subseteq k[F]$ forms a Gröbner basis of the algebra $k[{{\,\mathrm{HK}\,}}_{C_{n}}]$. Consequently, all $S'$-reduced words form a basis of $k[{{\,\mathrm{HK}\,}}_{C_{n}}]$.

As mentioned before, the fact that in the particular case of a cycle graph, even a finite Gröbner basis can be obtained, strengthens the assertion of Theorem 1.1 in view of [8].

We conclude with an example showing that the above result cannot be extended to arbitrary Hecke–Kiselman algebras of oriented graphs, even in the case of PI-algebras.

Example 4.5

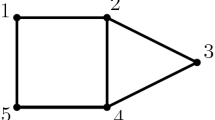
Let $\Theta$ be the graph obtained by adjoining an outgoing arrow to the cycle $C_3$:

then $V(\Theta )=\{a,b,c,d\}$ and we consider the deg-lex order on the free monoid $F=\langle a,b,c,d\rangle$ defined by $a<b<c<d$. Then the algebra $k[{{\,\mathrm{HK}\,}}_{\Theta }]$ does not have a finite Gröbner basis and it is a PI-algebra of Gelfand–Kirillov dimension 2.

Proof

It is easy to see that the set $N_{\Theta }$ used in the proof of Theorem 1.1 is the union of the following subsets of F:

• (i) $N_{(i)}= a\langle b,d\rangle a \cup b \langle c,d\rangle b \cup c\langle a,d\rangle c \cup d\langle b,c\rangle d$,

• (ii) $N_{(ii)}=a\langle c\rangle a \cup b\langle a,d\rangle b \cup c\langle b,d\rangle c \cup d\langle a,b,c\rangle d$,

• (iii) $N_{(iii)}= d\langle d \rangle b \cup d\langle d \rangle c$.

In particular, all words $d(abc)^kd, k\ge 1$, are in $N_{(ii)}$, but they do not have factors that are another words of $N_{\Theta }$. It follows that the algebra $k[{{\,\mathrm{HK}\,}}_{\Theta }]$ does not have a finite Gröbner basis (with respect to the indicated presentation and deg-lex order). By [10], this is a PI-algebra. Moreover, $k[C_{3}]$ is of linear growth with reduced words being factors of two infinite words $(abc)^{\infty }$ and $(acb)^{\infty }$ and reduced words in F are in the set $F'\cup F'dF'$, where $F'=\langle a,b,c\rangle \subseteq F$. So, ${{\,\mathrm{GKdim}\,}}(k[{{\,\mathrm{HK}\,}}_{\Theta }]) \le 2$. On the other hand, words of the form $(abc)^kd(abc)^m$, $k,m\ge 1$, do not have factors in $N_{\Theta }$, so they are reduced. Therefore ${{\,\mathrm{GKdim}\,}}(k[{{\,\mathrm{HK}\,}}_{\Theta }]) = 2$. $\square$