Skip to main content
SpringerLink
Log in

Computation of the effective thermal conductivity from 3D real morphologies of wood

  • Original Article
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

Abstract

This work is devoted to the numerical computation of the macroscopic properties of different wood species, namely the porosity and the effective thermal conductivity, following their orthotropic directions. We are interested in typical wood species, such as: spruce, poplar and balsa. First, each sample is scanned at a resolution on the order of the micrometer thanks to a lab X-ray nanotomograph (UltraTom by RX-solutions). Then, a suitable set of 3D image processing operations, coded as a Python script in ImageJ, allows obtaining a digital representation of the 3D morphology. This representation is used as an input mesh for a software developed in house, based on the finite volume method. We derive the macroscopic properties consisting of directional thermal conductivities by achieving the stationary regime. Several numerical experiments are carried out to validate the prediction approach. The focus will be on the effect of the representative elementary volume (REV) on the macroscopic property, which depends on the property itself (porosity, thermal conductivity), the species, and the material direction. An original volume reduction idea is proposed to improve the performance. It consists of amending the form and the size of the REV in the longitudinal direction by assuming that the phases are placed in parallel in this direction. It is numerically shown that this approach has a negligible impact on the property and greatly reduces the computational cost.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Wood handbook – Wood as an engineering material. U.S. Department of Agriculture, forest service. Forest Products Laboratory, Madison, WI, 2010.

  2. Woloszyn M, Rode C (2008) Tools for performance simulation of heat, air and moisture conditions of whole buildings. In: Building Simulation, Springer, pp 5–24

  3. Delgado J, Ramos NM, Barreira E et al (2010) A critical review of hygrothermal models used in porous building materials. Journal of Porous Media 13(3)

  4. Van Belleghem M, Steeman M, Willockx A et al (2011) Benchmark experiments for moisture transfer modelling in air and porous materials. Build Environ 46(4):884–898

    Article  Google Scholar 

  5. Perré P, Turner I (2001) Determination of the material property variations across the growth ring of softwood for use in a heterogeneous drying model. part 2. use of homogenisation to predict bound liquid diffusivity and thermal conductivity. Holzforschung 55(4):417–425

  6. Perré P, Almeida G, Ayouz M et al (2016) New modelling approaches to predict wood properties from its cellular structure: image-based representation and meshless methods. Ann For Sci 73(1):147–162

    Article  Google Scholar 

  7. Badel É, Perré P (2002) Predicting oak wood properties using X-ray inspection: representation, homogenisation and localisation. Part I: Digital X-ray imaging and representation by finite elements. Ann For Sci 59(7):767–776

  8. Baensch F, Zauner M, Sanabria SJ et al (2015) Damage evolution in wood: synchrotron radiation micro-computed tomography (SR\(\mu\)CT) as a complementary tool for interpreting acoustic emission (AE) behavior. Holzforschung 69(8):1015–1025

  9. Lux J, Delisée C, Thibault X (2006) 3D characterization of wood based fibrous materials: an application. Image Analysis & Stereology 25(1):25–35

  10. Standfest G, Kranzer S, Petutschnigg A et al (2010) Determination of the microstructure of an adhesive-bonded medium density fiberboard (MDF) using 3-D sub-micrometer computer tomography. J Adhes Sci Technol 24(8–10):1501–1514

    Article  Google Scholar 

  11. Zauner M, Stampanoni M, Niemz P (2016) Failure and failure mechanisms of wood during longitudinal compression monitored by synchrotron micro-computed tomography. Holzforschung 70(2):179–185

    Article  Google Scholar 

  12. Bucur V (2003) Nondestructive characterization and imaging of wood. Springer Science & Business Media

  13. Louërat M, Ayouz M, Perré P (2018) Heat and moisture diffusion in spruce and wood panels computed from 3-d morphologies using the lattice boltzmann method. Int J Therm Sci 130:471–483

    Article  Google Scholar 

  14. Perré P (2011) A review of modern computational and experimental tools relevant to the field of drying. Drying Technol 29(13):1529–1541

    Article  Google Scholar 

  15. Brodersen CR (2013) Visualizing wood anatomy in three dimensions with high-resolution X-ray micro-tomography (μCT)-a review-. IAWA J 34(4):408–424

    Article  Google Scholar 

  16. Forsberg F, Mooser R, Arnold M et al (2008) 3D micro-scale deformations of wood in bending: synchrotron radiation μCT data analyzed with digital volume correlation. J Struct Biol 164(3):255–262

    Article  Google Scholar 

  17. Van den Bulcke J, Boone M, Van Acker J et al (2009) X-ray tomography as a tool for detailed anatomical analysis. Ann For Sci 66(5):1–12

    Google Scholar 

  18. Hervé V, Mothe F, Freyburger C, et al (2014) Density mapping of decaying wood using x-ray computed tomography. Int Biodeterior Biodegrad 86:358–363

  19. Web source. https://www.jython.org/

  20. Web source. https://imagej.net/Fiji

  21. Díaz AR, Flores EIS, Yanez SJ et al (2019) Multiscale modeling of the thermal conductivity of wood and its application to cross-laminated timber. Int J Therm Sci 144:79–92

    Article  Google Scholar 

  22. Hunt JF, Gu H (2006) Two-dimensional finite heat transfer model of softwood. Part I. Effective thermal conductivity. Wood Fiber Sci 38(4):592–598

  23. Hunt JF, Gu H, Lebow PK (2008) Theoretical thermal conductivity equation for uniform density wood cells. Wood Fiber Sci 40:167–180

    Google Scholar 

  24. Sova D, Porojan M, Bedelean B et al (2018) Effective thermal conductivity models applied to wood briquettes. Int J Therm Sci 124:1–12

    Article  Google Scholar 

  25. Eymard R, Gallouët T, Herbin R (2000) Finite volume methods. In: Handbook of Numerical Analysis, vol 7. Elsevier, pp 713–1018

  26. Moukalled F, Mangani L, Darwish M (2016) The finite volume method in computational fluid dynamics: An Advanced Introduction with OpenFOAM and Matlab, vol 113. Springer

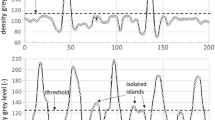
  27. Otsu N (1979) A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern 9(1):62–66

    Article  Google Scholar 

  28. Hornung U (1997) Miscible displacement. In: Homogenization and Porous Media. Springer, p 129–146

  29. Suquet PM (1985) Elements of homogenization for inelastic solid mechanics, vol 272. Springer-Verlag

    MATH  Google Scholar 

  30. Siau JF (1984) Transport processes in wood. Springer-Verlag

    Book  Google Scholar 

  31. Vay O, Busquets-Ferrer M, Emsenhuber G et al (2021) Thermal conductivity of untreated and chemically treated poplar bark and wood. Holzforschung 75(12):1125–1135

    Article  Google Scholar 

  32. Niemz P, Sonderegger W, Hering S et al (2010) Thermal conductivity of norway spruce and european beech in the anatomical directions. Annals of Warsaw University of Life Sciences-SGGW, Forestry and Wood Technology 72(72):66–72

    Google Scholar 

  33. Kotlarewski NJ, Ozarska B, Gusamo BK (2014) Thermal conductivity of papua new guinea balsa wood measured using the needle probe procedure. BioResources 9(4):5784–5793

    Article  Google Scholar 

Download references

Acknowledgements

this work is supported by SATT Pary-Saclay in the framework of the project Predict-BioMat. This study was carried out in the Centre Européen de Biotechnologie et de Bioéconomie (CEBB),supported by the Région Grand Est, Département de la Marne, Greater Reims and the European Union. In particular, the authors would like to thank the Département de la Marne, Greater Reims, Région Grand Est and the European Union along with the European Regional Development Fund (ERDF Champagne Ardenne 2014-2020) for their financial support of the Chair of Biotechnology of CentraleSupélec.

Author information

Authors and Affiliations

  1. Chair of Biotechnology, LGPM, CentraleSupélec, Centre Européen de Biotechnologie et de Bioéconomie (CEBB), 3 Rue des Rouges Terres, 51110, Pomacle, France

    El-Houssaine Quenjel & Patrick Perrée

Authors
  1. El-Houssaine Quenjel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Patrick Perrée
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed equally to the preparation of the manuscript, data collection and results analysis. They also read and approved the final version of the manuscript.

Corresponding author

Correspondence to El-Houssaine Quenjel.

Ethics declarations

Competing interests

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Quenjel, EH., Perrée, P. Computation of the effective thermal conductivity from 3D real morphologies of wood. Heat Mass Transfer 58, 2195–2206 (2022). https://doi.org/10.1007/s00231-022-03246-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-022-03246-7

Search

Navigation