1 Introduction

Microwave heating (MH) offers many advantages over convective heating (CH). Unlike CH, MH is direct, volumetric, selective and practically instantaneous [1]. Moreover, it can be more cost effective than CH, as shown in the previous work [2]. For these reasons, the use of MH can be more sensible than CH under certain operating conditions.

MH of a packed bed in a rectangular waveguide was widely investigated by Ratanadecho et al. A two-layered packed bed composed of the frozen and unfrozen layers was examined in [3, 4]. Two different configurations were tested—the frozen layer below and above the unfrozen layer. The results revealed that the direction of melting against the incident microwaves strongly depended on the configuration of the two-layered packed bed. In another paper, the microwave drying process was investigated [5]. The results showed that the variation of particle sizes and initial moisture content influences the degree of penetration and rate of microwave power absorbed within the sample. In turn, the effects of layered configuration, layered thickness, and operating frequency in different packed beds were numerically investigated in [6]. It was demonstrated that all these parameters have significant effect on temperature profiles in the packed bed. The effects of particle size, sample dimension, position inside the waveguide and microwave frequency in a saturated packed bed composed of glass beads and water were displayed in [7]. Recently, the effects of diameter, porosity, position and types of particles that have different thermal and dielectric in two-layered packed bed were studied [8]. It was concluded that the thermal and dielectric properties strongly influence heat transfer mechanism in each layer of the packed bed.

Zhu et al. studied MH of non-Newtonian fluids: apple sauce, skim milk and tomato sauce flowing in a circular [9] and rectangular [10] applicators. The applicators were located in a microwave cavity exited in TE10 mode at 915 MHz. A 3D mathematical model was developed to predict the distribution of electromagnetic field, dissipated power, temperature and velocity in the liquids. Electromagnetic field inside the cavity and liquids was described by Maxwell’s equations which were solved by finite difference time domain (FDTD) method while momentum and energy balances were calculated by the finite control volume method. The effects of dielectric properties of the fluid, the applicator geometry and its location in the microwave cavity were examined. Zhu et al. also investigated MH of a liquid carrying a single large solid particle [11] and multiple large particles [12] flowing in a circular applicator. The power absorption and temperature distributions in the liquid and particles were studied.

Two main approaches are applied in mathematical modelling to quantify the heat produced within a material due to microwaves: Maxwell’s equations [3–8] and the Lambert’s law [13–19]. While the former approach leads to determination of the spatial distribution of electromagnetic field, the latter one assumes an exponential decay of microwave power in the heated material. Although modelling based on the Lambert’s law gives only more or less approximate to the exact solution obtained with Maxwell’s equations, it is frequently used because of its simplicity. Nevertheless, the Lambert’s law gives rather reasonable results when a heated sample is thick enough, i.e. when the depth of a sample is larger than the penetration depth of microwaves.

It should be emphasised that a complete mathematical model of heat transfer in a packed bed subjected to MH should be composed of the coupled Maxwell’s and energy equations. The coupling is a consequence of the temperature dependence of the dielectric properties. The FDTD method is frequently used to solve Maxwell’s equations [3–12]. As the time scale for an integration of Maxwell’s equations at microwave frequencies is many orders of magnitude lower than the time scale for an integration of energy equation, an iterative procedure has to be established.

In this work, heat transfer in a packed column of nonporous particles due to MH and CH is investigated. Instead of the commonly used pseudo-homogeneous model the heterogeneous model was applied in the simulations of the packed column. Such the approach was motivated by the expected significant differences in the temperatures between the gas and solid phase. Therefore, transient one-dimensional mathematical models composed of the energy balance equations for the packed bed, gas and the column wall were formulated and numerically solved for the both heating methods. Because this study was focused rather on finding the differences between the both heating methods than finding the strict solution the Lambert’s law was employed in the modelling of MH to approximate the spatial variation of electromagnetic filed in the packed column. The calculations were carried out for the same electric power utilized for heating in the both packed columns. It gave the opportunity to compare the resulting temperature distributions under different heating conditions. Similar approach was applied in the previous work [2], which was aimed at determining the critical efficiency factors of microwave energy conversion into heat for different operating conditions. However, while a uniform temperature of the packed bed has been assumed in that prior work, the time and spatial distributions of temperature are taken into account in this work.

2 Mathematical model

This numerical study is based on two transient one-dimensional mathematical models for the microwave heated packed column (MHPC) and the convective heated packed column (CHPC). These models are composed of two sets of partial differential equations (PDEs) for the bed of particles, gas, and the column wall together with the appropriate sets of the initial and boundary conditions. Because of expected significant differences in the temperatures between the gas and the solid phase the heterogeneous model is employed in the simulations for the both packed columns.

Radial variations of temperature are not considered in the modelling as the generalized criterion is met [20, 21] (see also Table 1)

$$\frac{L}{{D_{i} }} > 0.04\frac{{\nu_{z} D_{i} }}{{D_{R} }} .$$
(1)

where L is the packed column length, D i is the inner diameter of the packed column, ν z is the average interstitial velocity, D R is the radial dispersion coefficient. This criterion has been validated for the two extreme limits of the particle Reynolds numbers which are characteristic for the performed simulations. When \(\text{Re}_{p}\) exceeds 100 the radial Peclet number Pe r equals 11 [22]. Therefore, the right hand side of the inequality (1) is about 4.4 in this case. In the other limit, as \(\text{Re}_{p}\) number is approx 36, the right hand side of this inequality is about 4. Comparing these results with the ratio L/D i , which equals 7.5 in these simulations, displays that the criterion (1) is satisfied in the range of applied conditions. Concluding, the transient one-dimensional heterogeneous mathematical models are used in the modelling to describe heat transfer in the both packed columns.

Table 1 Characteristics of the simulated system
Full size table

Axial dispersion of heat is neglected in the CHPC model since the particle Reynolds number is above 100 and L/d s ≥50. On the other hand, axial dispersion was taken into account in the MHPC model because much less intense gas flow rate is usually needed in such apparatus since heat is delivered to the packed bed not indirectly by convection but directly by microwaves.

The effective axial thermal conductivity, λ e,z , was calculated using the empirical formula proposed by Yagi [23]

$$\frac{{\lambda_{e,z} }}{{\lambda_{g} }} = \frac{{\lambda_{e,z}^{o} }}{{\lambda_{g} }} + 0.8\text{Re} \Pr$$
(2)

where λ g is the molecular thermal conductivity of gas, and λ o e,z is the effective static axial thermal conductivity. For the purpose of this work, the ratio λ o e,z /λ g was assumed to be 7.5 (as for glass beads in [23]). Please note that λ o e,z is attributed to the effective axial thermal conductivity in the particles, λ es , while λ e,z is assigned to the effective axial thermal conductivity in the gas, λ eg , in the MHPC model.

The proposed models give rather approximate solutions due to several assumptions made in the models formulations. They are as follows:

  1. I.

    Electromagnetics

    1. 1.

      The spatial distribution of dissipated microwave power in the packed column is approximated by the Lambert’s law.

    2. 2.

      The penetration depth of microwaves is a parameter of the MHPC model and it is assumed independent of temperature.

  1. II.

    Heat transfer

    1. 1.

      The axial dispersion of heat is neglected in the CHPC model and the plug flow is assumed.

    2. 2.

      The density, heat capacity and thermal conductivity of the column wall and particles are constant.

2.1 Characteristics of the simulated packed bed

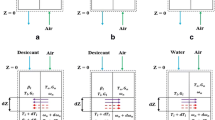
As it was mentioned earlier, two different heating methods of the packed column are compared in the numerical simulations. They are schematically shown in Fig. 1. The dimensions of the packed column are displayed in Fig. 2 and characteristics of the system are summarized in Table 1.

Fig. 1
figure 1

Schematic diagram of the MHPC—the upper half of the figure, and the CHPC—the bottom half of the figure

Full size image
Fig. 2
figure 2

Schematic diagram of the simulated packed column. D i  = 0.2 m, D o  = 0.22 m, L = 1 m

Full size image

While heat is supplied to the packed column with a preheated convective gas stream in the CHPC, it is produced directly by microwaves in the MHPC. The theoretical efficiency factor of electrical energy conversion into heat is 1 because all the energy embodied in the electric current is converted into heat in the resistance wire of a heater [24]. However, the heater is usually equipped with a fan blowing the heat off the wire. As the fan consumes some electric energy, the total efficiency factor for the heater is lower than 1. In this model, the assumed total efficiency factor of electrical energy conversion into heat, η el→heat , is 0.95. In turn, the efficiency factor η el→mw describes the effectiveness of electrical energy conversion into microwaves. The reported values of the factor for magnetrons are: 0.5 [25], 0.5–0.65 [26], 0.6–0.7 [27], 0.8 [28]. In this work, the conservative value of the factor was assumed.

2.2 Governing equations

This section presents balance equations for heat transfer in the MHPC and CHPC.

  1. 1.

    The energy balance in the bed of particles can be written for the MHPC as:

$$\left( {1 - \varepsilon } \right)\rho_{s} c_{ps} \frac{{\partial T_{s} }}{\partial t} = \lambda_{es} \frac{{\partial^{2} T_{s} }}{{\partial z^{2} }} + \frac{{6\left( {1 - \varepsilon } \right)}}{{d_{s} }}h_{g} \left( {T_{g} - T_{s} } \right) + \dot{Q}_{mw}$$
(3)

where ε is the porosity of the packed bed, ρ s is the density of particles, c ps is the specific heat of particles, T s is the temperature of particles, T g is the gas temperature, λ es is the effective thermal conductivity of the particles, d s is the particle diameter, h g is the heat transfer coefficient between the particles and gas, Q mw is the local volumetric heat dissipation due to microwaves.

The spatial distribution of the dissipated microwave power in the packed bed was approximated by the Lambert’s law [17]

$$\dot{Q}_{mw} = \frac{{P_{0} }}{{FD_{p} }}\exp \left( { - \frac{z}{{D_{p} }}} \right)$$
(4)

where P 0 is the incident microwave power at the inlet face of the packed column, F is the surface area of the inlet face, D p is the penetration depth given by the following equation

$$D_{p} = \frac{{\lambda_{0} }}{{2\pi \sqrt {(2\varepsilon^{\prime})} }}\frac{1}{{\sqrt {\left( {\sqrt {1 + \left( {\frac{{\varepsilon^{\prime\prime}}}{{\varepsilon^{\prime}}}} \right)^{2} } - 1} \right)} }}$$
(5)

where λ 0 is the wavelength of microwaves, ε′ is the dielectric constant, ε″ is the dielectric loss.

In the case of the CHPC model, the local volumetric heat dissipation due to microwaves, \(\dot{Q}_{mw}\), has to be omitted in the balance Eq. (3). Also, the first term in the right hand side of Eq. (3) vanishes since axial dispersion of heat can be neglected.

  1. 2.

    The energy balance in the gas phase is formulated for the MHPC as

$$\varepsilon \rho_{g} c_{pg} \left( {\frac{{\partial T_{g} }}{\partial t} + v_{z} \frac{{\partial T_{g} }}{\partial z}} \right) = \lambda_{eg} \frac{{\partial^{2} T_{g} }}{{\partial z^{2} }} + \frac{{6\left( {1 - \varepsilon } \right)}}{{d_{s} }}h_{g} \left( {T_{s} - T_{g} } \right) + \frac{4}{{D_{i} }}h_{i} \left( {T_{w} - T_{g} } \right) .$$
(6)

where ρ g is the gas density, c pg is the specific heat of gas, λ eg is the effective thermal conductivity of the gas phase, T g is the gas temperature, T w is the wall temperature, h i is the heat transfer coefficient between the gas and wall, D i is the inner diameter of the packed column.

In the case of the CHPC model the first term in the right hand side of Eq. (6) vanishes since axial dispersion of heat can be neglected.

  1. 3.

    The energy balance in the column wall is defined for the both packed columns as:

$$\rho_{w} c_{pw} \frac{{\partial T_{w} }}{\partial t} = \lambda_{w} \frac{{\partial^{2} T_{w} }}{{\partial z^{2} }} + \frac{4}{{D_{i} }}h_{i} \left( {T_{g} - T_{w} } \right) - \frac{4}{{D_{o} }}h_{o} \left( {T_{w} - T_{a} } \right)$$
(7)

where ρ w is the wall density, c pw is the specific heat of the wall, λ w is the thermal conductivity of the wall, T a is the ambient temperature, h o is the heat transfer coefficient between the wall and the surrounding air, D o is the outer diameter of the packed column.

The electric power needed to produce the incident microwave power, P 0, with the efficiency of energy conversion η el→mw can be defined as follows:

$$P_{el} = \frac{{P_{0} }}{{\eta_{el \to mw} }}$$
(8)

where η el→mw is the efficiency factor of electrical energy conversion into microwaves.

The electric power needed to preheat a flowing gas from the ambient temperature to the inlet temperature can be expressed as follows:

$$P_{el} = \frac{\dot{m}_{CH}}{\eta_{el \to heat}} \int\limits_{{T_{a} }}^{{T_{gin} }} {c_{pg} } dT$$
(9)

where \(\dot{m}_{CH}\) is the gas mass flow rate, and η el→heat is the efficiency factor of electrical energy conversion into heat.

2.3 Initial and boundary conditions

The initial and boundary conditions have to be specified to solve the appropriate sets of the balance equations for the MHPC and CHPC. They are summarized in Table 2. Initially, the column wall, bed of particles and gas are assumed to be in thermal equilibrium with the ambient air. Therefore, their initial temperatures are identical. Regarding the boundary conditions for the MHPC model, the classical Danckwerts condition was applied for the packed bed and the column wall at the inlet and outlet faces of the column. In turn, Dirichlet conditions were set at the inlet boundary and Danckwerts condition at the outlet boundary for the gas. In the case of the CHPC model some boundary conditions vanish because axial dispersion of heat can be neglected (see Table 2 for details).

Table 2 Initial and boundary conditions for the MHPC and CHPC
Full size table

2.4 Numerical procedure

The proposed two sets of balance equations for the MHPC and CHPC are PDEs [except simplified Eq. (3) ordinary differential equation (ODE) for the CHPC]. The method of lines (MOL) along with the uniform grid finite-difference technique was used to obtain the temperature distributions in time and space [29]. More strictly, the MOL was applied for the spatial discretization in one-dimensional domain and integration in time of the resulting system of ODEs. A grid sensitivity analysis was performed. Based on this analysis a chosen final number of axial grid points was 400. A fourth-order (five point) biased-upwind finite-difference and a fourth-order (five point) centered finite-difference approximation were applied for the first spatial derivative ∂T g /∂z and the second spatial derivatives ∂2 T s /∂z 2, ∂2 T w /∂z 2, respectively. A stagewise differentiation was used to calculate the second derivatives. An efficient variable order solver based on the numerical differentiation formulas (ode15 s) was employed to integrate the systems of ODEs in Matlab (The MathWorks, Inc.).

It should be stressed that the resulting temperature distributions for the MHPC and CHPC were compared using the criterion according to which the electric power for the both methods must be the same (Eqs. 6, 7).

3 Results and discussion

A numerical integration of the model equations for the MHPC and CHPC using the criterion mentioned in the previous section gave the temperature distributions in the packed bed, gas and the wall of the packed column (Figs. 3, 4, 5). Since a comparison of the packed bed temperatures between the MHPC and CHPC using the profiles presented in Fig. 3 is quite inconvenient, to simplify interpretation of the results, an unambiguous criterion was introduced—the average bed temperature

$$\bar{T}_{s} = \frac{1}{L}\int\limits_{0}^{L} {T_{s} dz} .$$
(10)
Fig. 3
figure 3

Comparison of the bed temperatures for the MHPC (dotted lines) and CHPC (solid lines). The simulation parameters: \(T_{gin,CH} = 320 \, \text{K}\), \(T_{gin,MH} = 293 \, \text{K}\), \(P_{0} = 1478 \, \text{W}\), D p /L = 0.5, ε = 0.5. The electric power for the both methods was approx 2.96 kW

Full size image
Fig. 4
figure 4

Comparison of the gas temperatures for the MHPC (dotted lines) and CHPC (solid lines). For the simulation parameters see Fig. 3. The electric power for the both methods was approx 2.96 kW

Full size image
Fig. 5
figure 5

Comparison of the column wall temperatures for the MHPC (dotted lines) and CHPC (solid lines). For the simulation parameters see Fig. 3. The electric power for the both methods was approx 2.96 kW

Full size image

Concerning the gas phase, time profiles of the outlet gas temperature are also more convenient for discussion of the results than the distributions presented in Fig. 4. All recalculated profiles are presented in Figs. 6 and 7. As follows from these figures the steady state was reached in the CHPC after approx 800 s. On the other hand the average bed temperature and the outlet gas temperature increase constantly in the MHPC. Obviously, it is due to the absorbed microwave power which is higher than the heat power lost from the system. It should be noted that the average bed temperature is higher for the CHPC than MHPC up to approx 850 s at the same electric powers applied; the opposite situation is for longer times.

Fig. 6
figure 6

Comparison of the average bed temperature vs. time for the MHPC (dotted lines) and CHPC (solid lines). For the simulation parameters see Fig. 3. The electric power for the both methods was approx 2.96 kW

Full size image
Fig. 7
figure 7

Comparison of the outlet gas temperature vs. time for the MHPC (dotted lines) and CHPC (solid lines). For the simulation parameters see Fig. 3. The electric power for the both methods was approx 2.96 kW

Full size image

In the next sections the effects of different operating conditions on the performance of the packed columns are presented. The conditions of the performed simulations are summarized in Table 3. Please notice that because of the same electric power used in the both packed columns, each inlet gas temperature corresponds to the different incident microwave power in Table 3.

Table 3 Conditions of the performed numerical simulations
Full size table

3.1 Effect of the gas inlet temperature

The effect of the gas inlet temperature on the average bed temperature and the outlet gas temperature are displayed in Figs. 8 and 9, respectively. The numerical simulations were performed for three different gas inlet temperatures: 320, 373 and 413 K and the related incident microwave powers (see Table 3). Two ranges can be distinguished in the compared profiles of the average bed temperature in Fig. 8. A transition between them is determined from the intersection of the corresponding temperature profiles for the CHPC and MHPC. It is typical for the obtained results that the transition is always in the second section of the temperature profile for the CHPC. Comparing both corresponding profiles it can be concluded that the average bed temperature is higher for the CHPC than MHPC in the first range, while the opposite relation is observed in the second range.

Fig. 8
figure 8

Influence of the inlet gas temperatures and the related incident microwave powers on the average bed temperatures in the CHPC (solid lines) and MHPC (dotted lines). The corresponding simulations performed for the same electric power utilized in MH and CH

Full size image
Fig. 9
figure 9

Influence of the inlet gas temperatures and the related incident microwave powers on the outlet gas temperatures in the CHPC (solid lines) and MHPC (dotted lines). The corresponding simulations performed for the same electric power utilized in the both methods

Full size image

The results displayed in Fig. 9 are also of interest. One can distinguish three ranges in the outlet gas temperature profiles. While the temperature in the first and third range is higher for the MHPC than CHPC, this relationship is reversed in the second range.

3.2 Effect of the bed porosity

The effect of bed porosity on the average bed temperature and the outlet gas temperature are displayed in Figs. 10 and 11. The simulations were performed for three different bed porosities: 0.2, 0.5 and 0.8. Please note that the character of the temperature profiles in Figs. 10 and 8 is the same. However, instead of the gas inlet temperature, the bed porosity affects the new results in Fig. 10. It can be seen from this figure that when the bed porosity increases, the average bed temperature increases as well. Two effects should be taken into account to understand this behavior. The first one is related to the change in the heat capacity of the solid particles per unit volume of the bed, (1 − ε)ρ s c ps . Please note that this term decreases with the bed porosity increase. As a result the bed temperature in the both packed columns is more susceptible to changes in the heating conditions. The second effect is related to the decrease of the specific surface area of the packed bed and the interstitial velocity with the increasing bed porosity. Naturally, it leads to deterioration of the heat transfer between the bed and the gas. In the case of the MHPC, in which heat is produced directly in the packed bed, this deterioration of the heat transfer even increases accumulation of heat in the packed bed. In turn, in the case of the CHPC, in which heat is transferred from the hot gas to the packed bed, this deterioration of the heat transfer has to be a limiting factor. However, it is less influential than the former effect as it is apparent from Fig. 10. Concluding, the heat capacity of the solid particles per unit volume of the bed, (1 − ε)ρ s c ps is the deciding factor when analyzing an influence of the bed porosity on the average bed temperature in the both packed columns.

Fig. 10
figure 10

Influence of the bed porosity on the average bed temperatures in the CHPC (solid lines) and MHPC (dotted lines). The corresponding simulations performed for the same electric power utilized in MH and CH

Full size image
Fig. 11
figure 11

Influence of the bed porosity on the outlet gas temperatures in the CHPC (solid lines) and MHPC (dotted lines). The corresponding simulations performed for the same electric power utilized in the both methods

Full size image

Naturally, the time profiles of the outlet gas temperature shown in Fig. 11 are closely related to the corresponding time profiles of the average bed temperature presented in Fig. 10. Therefore, the former profiles present exactly the same dependence on the bed porosity.

3.3 Effect of the penetration depth

The effect of the penetration depth of microwaves on the average bed temperature and the outlet gas temperature is shown in Figs. 12 and 13. The simulations were performed for three different ratios D p /L: 0.2, 0.5 and 0.8. At the first glance, it might seem puzzling that the average bed temperatures calculated for these penetration depths with Eq. (10) and presented in Fig. 12 differ. The answer is the definition of the penetration depth, which is known as the characteristic distance at which the power density decreases to 37 % of its initial value at the surface (see Eq. 3). As a consequence, when the ratio D p /L increases, an amount of microwave energy which is transmitted through the bed and is lost to the surrounding air also increases. In the extreme case, when the ratio D p /L is equal 1, the power density at the far end of the packed column decreases to 37 % of its initial value at the surface (see Table 3). This effect explains the higher rates of the temperature increase for the lower ratios D p /L.

Fig. 12
figure 12

Influence of the ratio D p /L on the average bed temperatures in the CHPC (solid lines) and MHPC (dotted lines). The corresponding simulations performed for the same electric power utilized in MH and CH

Full size image
Fig. 13
figure 13

Influence of the ratio D p /L on the outlet gas temperatures in the CHPC (solid lines) and MHPC (dotted lines). The corresponding simulations performed for the same electric power utilized in the both methods

Full size image

Please note that the microwave energy distribution also has a clear impact on the outlet gas temperature profiles (Fig. 13). With the decreasing ratio D p /L the outlet gas temperature decreases as well. It is a result of the packed bed temperature distribution in which the highest temperatures are shifted towards the entrance of the packed column while the packed bed on the other side of the column has relatively low temperatures. Naturally, the gas temperature corresponds to the solid temperature. It is worth noting that when the ratio D p /L decreases MH is especially advantageous since the difference between the average bed temperature and the outlet gas temperature increases. It means that less heat is removed from the column with the convective gas stream (Table 4).

Table 4 Ratios of microwave powers dissipated in the bed and the incident microwave power for different D p /L
Full size table

3.4 Effect of gas velocity

The effect of gas velocity on the average bed temperature and the outlet gas temperature is presented by changing the following Y ratio in the simulations

$$Y = {{\dot{m}_{CHPC} } \mathord{\left/ {\vphantom {{\dot{m}_{CHPC} } {\dot{m}_{MHPC} }}} \right. \kern-0pt} {\dot{m}_{MHPC} }} .$$
(11)

The defined Y ratio only affects the gas mass flow rate for the CHPC because the constant gas mass flow rate has been assumed for the MHPC (see Table 1). Please note that a change in the mass flow rate for the fixed bed porosity also changes the gas velocity which, in turn, influences heat transfer between the gas and the packed bed.

The simulation results carried out for different Y ratios are shown in Figs. 14 and 15. The character of the temperature profiles is the same as in the previous figures. Heat transfer between the gas and the packed bed is enhanced when the gas velocity increases. This effect accounts for the temperatures of the gas and bed that increase with the increasing Y ratios in the CHPC. However, when the gas mass flow rate increases in the CHPC, the electricity consumption predicted by Eq. (9) also increases. To meet the criterion of the same electric power applied in the both packed columns the incident microwave power has to be recalculated for every simulation. The recalculated microwave powers are summarized in Table 3. Obviously, an increase of the microwave power fully explains the observed effect of the increasing bed and gas temperatures for increasing Y ratio.

Fig. 14
figure 14

Influence of Y ratio on the average bed temperatures in the CHPC (solid lines) and MHPC (dotted lines). The corresponding simulations performed for the same electric power utilized in MH and CH

Full size image
Fig. 15
figure 15

Influence of Y ratio on the outlet gas temperatures in the CHPC (solid lines) and MHPC (dotted lines). The corresponding simulations performed for the same electric power utilized in the both methods

Full size image

4 Conclusions

The following conclusions can be drawn from the numerical simulations of the heat transfer under the same electric powers utilized in the MHPC and the CHPC:

  1. 1.

    Two ranges can be distinguished in the corresponding profiles of the average bed temperature for the CHPC and MHPC. The transition between these ranges can be determined from the intersection of those profiles. It is typical for the compared profiles that the temperature in the first range is higher for the CHPC than MHPC, while the opposite relationship is observed in the second range. Therefore, when longer heating times are expected, the MHPC should be preferred. This transition time depends on all examined parameters being: the ratio of the penetration depth of microwaves and the column length, the incident microwave power and the inlet gas temperature, the bed porosity and the Y ratio.

  2. 2.

    Three ranges can be distinguished in the corresponding outlet gas temperature profiles for the CHPC and MHPC. The transitions between these ranges can be found in the above described manner. It is typical for the compared profiles that the outlet gas temperature is higher for the MHPC than CHPC in the first and the third range, while it is lower for the MHPC than CHPC in the second range. The outlet gas temperature decreases with decreasing the incident microwave power, the bed porosity and the ratio of the penetration depth of microwaves and the column length.