Skip to main content
SpringerLink
Log in

Maximum thermal conductance for a micro-channel, utilising Newtonian and non-Newtonian fluid

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

Abstract

This paper investigates the thermal behaviour of two micro-channel elements cooled by Newtonian and non-Newtonian fluids, with the objective to maximise thermal conductance subject to constraints. This is done firstly for a two-dimensional duct micro-channel and secondly for a three-dimensional complex micro-channel. A numerical model is used to solve the governing equations relating to flow and temperature fields for both cases. The geometric configuration of each cooling channel is optimised for Newtonian and non-Newtonian fluid at a fixed inlet velocity and heat flux. In addition, the effect of porosity on thermal conductance is investigated. It was found, in both cases, that the non-Newtonian fluid characteristics result in a significant variation in thermal conductance as inlet velocity is increased. The characteristics of a dilatant fluid greatly reduce thermal conductance on account of shear thickening on the boundary surface. In contrast, a pseudoplastic fluid shows increased thermal conductance. A comparison of the complex micro-channel and the duct micro-channel shows the improved thermal conductance resulting from greater flow access to the conductive area, achieved by the complex micro-channel.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Abbreviations

A :

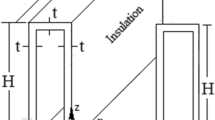
Total channel area (m2)

C :

Global thermal conductance

C p :

Specific heat (J/K)

d :

Channel depth (m)

D 1 :

Diameter of channel before branching (m)

D 2 :

Diameter of channel after branching (m)

H :

Total channel height (m)

k :

Thermal conductivity (W/m K)

K :

Consistency (Pa s0.5)

L :

Total channel length (m)

L 1 :

Length of channel before branching (m)

L 2 :

Length of channel after branching (m)

n :

Power law index

P :

Pressure (Pa)

q :

Total heat transfer (W)

R :

Global thermal resistance

Re :

Reynolds number

T :

Temperature (K)

U :

Average velocity (m/s)

\( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{U} \) :

Velocity vector (m/s)

V :

Total channel volume (m3)

α :

Ratio of L 1 to L

\( \dot{\gamma } \) :

Rate of strain

θ :

Angle between branches (radians)

μ :

Viscosity (kg/m s)

ρ :

Density (kg/m3)

φ :

Porosity ratio

~:

Dimensionless variable

max :

Maximum

in :

Inlet

References

  1. Mudawar I (2001) Assessment of high-heat-flux thermal management schemes. IEEE Trans Compon Packag Technol 24:122–141

    Article  Google Scholar 

  2. Rahman MM (2000) Measurement of heat transfer in microchannel heat sinks. Int Commun Heat Mass Transf 27:495–506

    Article  Google Scholar 

  3. Toh KC, Chen XY, Chai JC (2002) Numerical computation of fluid flow and heat transfer in microchannels. Int J Heat Mass Transf 45:5133–5141

    Article  MATH  Google Scholar 

  4. Li J, Peterson GP (2007) 3-Dimensional numerical optimization of silicon-based high performance parallel microchannel heat sink with liquid flow. Int J Heat Mass Transf 50:2895–2904

    Article  MATH  Google Scholar 

  5. Fedorov AG, Viskanta R (2000) Three-dimensional conjugate heat transfer in the microchannel heat sink for electronic packaging. Int J Heat Mass Transf 43:399–415

    Article  MATH  Google Scholar 

  6. Jung J, Oh H, Kwak H (2009) Forced convective heat transfer of nanofluids in microchannels. Int J Heat Mass Transf 52:466–472

    Article  Google Scholar 

  7. Chein R, Huang G (2005) Analysis of microchannel heat sink performance using nanofluids. Appl Therm Eng 25:3104–3114

    Article  Google Scholar 

  8. Wen D, Ding Y (2004) Experimental investigation into convective heat transfer of nanofluids at the entrance region under laminar flow conditions. Int J Heat Mass Transf 47:5181–5188

    Article  Google Scholar 

  9. Barkhordari M, Etemad SG (2007) Numerical study of slip flow heat transfer of non-Newtonian fluids in circular microchannels. Int J Heat Mass Transf 28:1027–1033

    Google Scholar 

  10. Kim HW, Jeng DR, DeWitt KJ (1983) Momentum and heat transfer in power-law fluid flow over two dimensional or axisymmetrical bodies. J Heat Transf 26(2):245–259

    Article  MATH  Google Scholar 

  11. Das S, Chakraborty S (2006) Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal Chim Acta 559:15–24

    Article  Google Scholar 

  12. Bello-Ochende T, Liebenberg L, Meyer JP (2007) Constructal cooling channels for micro-channel heat sinks. Int J Heat Mass Transf 50:4141–4150

    Article  MATH  Google Scholar 

  13. Bejan A (2006) Constructal theory of pattern formation. Hydrol Earth Syst Sci Dis 3(4):1773–1807

    Article  Google Scholar 

  14. Bejan A (2006) Constructal theory of design in engineering and nature. Therm Sci 10(1):9–18

    Article  Google Scholar 

  15. Bejan A, Lorente S (2006) Constructal theory of generation of configuration in nature and engineering. J Appl Phys 100(4). doi:10.1063/1.2221896

  16. Bello-Ochende T, Meyer JP, Ighalo FU (2010) Combined numerical optimization and constructal theory for the design of microchannel heat sinks. Numerical Heat Transfer, Part A 58:882–899

    Article  Google Scholar 

  17. Bejan A, Lorente S (2008) Design with constructal theory. Wiley, USA

    Book  Google Scholar 

  18. Balmforth NJ, Craster RV (2001) Geophysical aspects of non-Newtonian fluid mechanics. In: Balmforth NJ, Provenzale A (eds) Geomorpholohical Fluid Mechanics, Lecture Notes in Physics, vol 582. Springer, Heidelberg, pp 34–51

  19. CD-Adapco (2011) StarCCM+ user guide 6.02.007

  20. Hess WR (1914) Das Prinzip des kleinsten Kraftverbrauches im Dienste hämodynamischer Forschung. Archiv für Anatomie und Physiologie 1914:1–62

    Google Scholar 

  21. Murray CD (1926) The physiological principle of minimum work. The vascular system and the cost of blood volume. Proc Natl Acad Sci USA 12:207–214

    Article  Google Scholar 

  22. Qu W, Mudawar I (2002) Analysis of three-dimensional heat transfer in micro-channel heat sinks. Int J Heat Mass Transf 45:3973–3985

    Article  MATH  Google Scholar 

Download references

Acknowledgments

The authors acknowledge with gratitude the funding obtained from the NRF, TESP, University of Stellenbosch/University of Pretoria, SANERI/SANEDI, CSIR EEDSM Hub and NAC and the National Research Foundation (NRF-DST), as well as support from Aerotherm.

Author information

Authors and Affiliations

  1. Department of Mechanical and Aeronautical Engineering, University of Pretoria, Private Bag X20, Hatfield, Pretoria, 0028, South Africa

    M. D. Stocks & J. P. Meyer

  2. Department of Mechanical Engineering, University of Cape Town, Private Bag X3, Rondebosch, 7701, South Africa

    T. Bello-Ochende

Authors
  1. M. D. Stocks
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Bello-Ochende
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. P. Meyer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to T. Bello-Ochende.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Stocks, M.D., Bello-Ochende, T. & Meyer, J.P. Maximum thermal conductance for a micro-channel, utilising Newtonian and non-Newtonian fluid. Heat Mass Transfer 50, 865–875 (2014). https://doi.org/10.1007/s00231-014-1298-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-014-1298-0

Keywords

Search

Navigation