Skip to main content
SpringerLink
Log in

Thermal analysis of thin multi-layer metal films during femtosecond laser heating

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

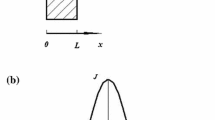
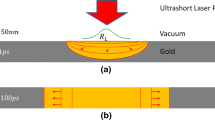
Abstract

Multi-layer metals films are widely used in modern engineering applications such as gold-coated metal mirrors used in high power laser systems. A transient heat flux model is derived to analyze multi-layer metal films under laser heating. The two separate system composed of electrons and the lattice is considered to take into account the electron–lattice interaction. The present model predicted the effects of underlying chromium’s thermal properties on temperature rise of the top gold layer. The effects of two adjacent and different metals with different electron–lattice coupling factors are analyzed for the heating mechanism of different lattices. The derived transient model combined with the two different conservation equations for the lattice and electrons are applied for the ultra short-pulse laser heating of a multi-layer film composed of gold and chromium.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Abbreviations

C :

Heat capacity (J m−3 K−1)

G :

Electron lattice coupling factor (W m−3 K−1)

J :

Laser pulse intensity (J m−3)

k B :

Boltzmann constant (J K−1)

L :

Film thickness (m)

Q :

Heat flux (W m−2)

R :

Surface reflectivity

S :

Source term (W m−3)

t :

Time (s)

t p :

Laser pulse duration (s)

T :

Temperature (K)

x :

Spatial coordinate (m)

δ :

Radiation penetration depth (m)

κ :

Thermal conductivity (W m−1 K−1)

τ :

Electron relaxation time (s)

E:

Electron

L:

Lattice

References

  1. Qiu TQ, Tien CL (1992) Short-pulse laser heating of metals. Int J Heat Mass Transfer 35:719–726

    Article  Google Scholar 

  2. Qiu TQ, Tien CL (1994) Femtosecond laser heating of multi layer metals. I. Analysis. Int J Heat Mass Transfer 37(17):2789–2797

    Article  Google Scholar 

  3. Majumdar A (1998) Microscale energy transport in solids. In: Tien CL, Majundar A, Gerner FM (eds) Microscale energy transport. Taylor & Francis, Washington, DC, pp 3–93

  4. Yilbas BS (2002) Short-pulse laser heating of gold–chromium layers: thermo-elasto-plastic analysis. J Phys D Appl Phys 35:1210–1217

    Article  Google Scholar 

  5. Musikant S (1985) Optical materials: an introduction to selection and application. Marcel-Dekker, New York

    Google Scholar 

  6. Joseph EE, Presiozi L (1989) Heat waves. Rev Mod Phys 61:41–73

    Article  MATH  Google Scholar 

  7. Maurer MJ (1969) Relaxation model for heat conduction in metals. J Appl Phys 40(13):5123–5130

    Article  Google Scholar 

  8. Kaganov MI, Lifshitz IM, Tanatarov LV (1957) Relaxation between electrons and the crystalline lattice. Sov Phys JETP 4:173–178

    MATH  Google Scholar 

  9. Anisimov SI, Kapeliovich BL, Perel’man TL (1974) Electron emission from metal surfaces exposed to ultra short laser pulses. Sov Phys JETP 39:375–377

    Google Scholar 

  10. Qiu TQ, Tien CL (1993) Heat transfer mechanisms during short-pulse laser heating of metals. ASME J Heat Transfer 115:835–842

    Article  Google Scholar 

  11. Ziman JM (1965) Principles of the theory of solids. Cambridge University Press, Cambridge

    Google Scholar 

  12. Yilbas BS (2001) Material response to thermal loading due to short pulse laser heating. Int J Heat Mass Transfer 44:3787–3798

    Article  MATH  Google Scholar 

  13. Yilbas BS (2002) Laser short-pulse heating of gold–copper two-layer assembly: thermo-elasto-plastic analysis. Jpn J Appl Phys 41:5226–5234

    Article  Google Scholar 

  14. Wilson AH (1954) The theory of metals, 2nd edn. Cambridge University Press, New York

    Google Scholar 

  15. Ziman JM (1960) Electrons and phonons: the theory of transport phenomena in solids. Clarendon Press, Oxford

    MATH  Google Scholar 

  16. Majumdar A (1993) Microscale heat conduction in dielectric thin films. ASME J Heat Transfer 115:7–16

    Article  Google Scholar 

  17. Goodson KE (1996) Thermal conduction in nonhomogeneous CVD diamond layers in electronic microstructures. ASME J Heat Transfer 118:279–286

    Article  Google Scholar 

  18. Fujimoto JG, Liu JM, Ippen EP (1984) Femtosecond laser interaction with metallic tungsten and nonequilibrium electron and lattice temperatures. Phys Rev Lett 53:1840–1847

    Article  Google Scholar 

  19. Elsayed-Ali HE, Norris TB, Pessot MA, Mourou GA (1987) Time resolved observation of electron–phonon relaxation in copper. Phys Rev Lett 58:1212–1215

    Article  Google Scholar 

  20. Brorson SD, Fujimoto JG, Ippen EP (1987) Femtosecond electronic heat transfer dynamics in thin gold film. Phys Rev Lett 59:1062–1065

    Article  Google Scholar 

  21. Allen PB (1987) Theory of thermal relaxation of electrons in metals. Phys Rev Lett 59:1460–1463

    Article  Google Scholar 

  22. Elsayed-Ali HE, Jushasz T (1993) Femtosecond time-resolved thermomodulation of thin gold films with different crystal structures. Phys Rev B 47:13599–13610

    Article  Google Scholar 

  23. Eesley GL (1986) Observation of nonequilibrium electron and lattice temperatures in copper by picosecond laser pulses. Phys Rev B 33:2144–2151

    Article  Google Scholar 

  24. Scouler WJ (1967) Temperature modulated reflectance of gold from 2 to 10 eV. Phys Rev Lett 18:445–448

    Article  Google Scholar 

  25. Chapman S, Cowling TG (1953) The mathematical theory of non-uniform gases. Cambridge University Press, Cambridge

Download references

Acknowledgments

The authors would like to acknowledge Deniz Seker, M.S. for his contribution on computer applications.

Author information

Authors and Affiliations

  1. University of California at Davis, Davis, USA

    A. Karakas

  2. Department of System Engineering, Yeditepe University, Kayısdag, 81130, Istanbul, Turkey

    M. Tunc

  3. Mechanical Engineering Department, Faculty of Engineering and Architecture, Abant Izzet Baysal University, Golkoy Campus, 14280, Bolu, Turkey

    Ü. Camdali

Authors
  1. A. Karakas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Tunc
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ü. Camdali
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ü. Camdali.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Karakas, A., Tunc, M. & Camdali, Ü. Thermal analysis of thin multi-layer metal films during femtosecond laser heating. Heat Mass Transfer 46, 1287–1293 (2010). https://doi.org/10.1007/s00231-010-0653-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-010-0653-z

Keywords

Search

Navigation