Skip to main content
SpringerLink
Log in

Numerical simulation of fluid flow and heat transfer characteristics in channel with V corrugated plates

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

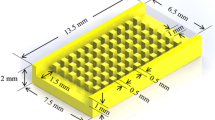
Abstract

A detailed numerical study is carried out to investigate fluid flow and heat transfer characteristics in a channel with heated V corrugated upper and lower plates. The parameters studied include the Reynolds number (Re = 2,000–5,500), angles of V corrugated plates (θ = 20°, 40°, 60°), and constant heat fluxs (q″ = 580, 830, 1,090 W/m2). Numerical results have been validated using the experimented data reported by Naphon, and a good agreement has been found. The angles of V corrugated plates (θ) and the Reynolds number are demonstrated to significantly affect the fluid flow and the heat transfer rate. Increasing the angles of V corrugated plates can make the heat transfer performance become better. The increasing Reynolds number leads to a more complex fluid flow and heat transfer rate. The numerical calculations with a non-equilibrium wall function have a better accuracy than with a standard wall function for solving high Reynolds numbers or complex flow problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Abbreviations

A :

Area

A c :

The surface area of corrugated plate

A cross :

The cross section area of channel

C1, C2, C μ :

Turbulent constant

C p :

Specific heat (J/kg K)

D h :

Hydraulic diameter (m)

E :

Enhancement ratio

H :

The height of the channel

h c :

Mean heat transfer coefficient (W/m2 K)

I :

Turbulence intensity

k f :

Thermal conductivity of fluid (W/m K)

k S :

Thermal conductivity of solid (W/m K)

k :

Turbulent kinetic energy (m2/s2)

Nu :

Nusselt number (\( Nu = h_c H \bar{\sigma }/2k_f \bar{X} \))

m a :

The air mass flow rate

n :

Normal vector

P :

Pressure (atm)

P c :

Wetted perimeter of the channel (m)

Pr :

Prandtl number

Q a :

Heat transferred to the cooling air form the corrugated plates (W)

Q heater :

Heat flux added to the top and bottom corrugated plates (W)

q″:

Heat flux (W/m2)

Re :

Reynolds number (Re = uD h /υ)

T a :

Mean temperature of air (°C)

T in :

Temperature of inlet (°C)

T s :

Mean temperature of surface (°C)

\( \bar{u}_{i} ,\;\bar{u}_{j} \) :

Velocity component (m/s)

u in :

Mean velocity of inlet (m/s)

\( \bar{X} \) :

The distance of the corrugated plate (m)

x i , x j :

Coordinate (m)

ρ :

Density (kg/m3)

μ l , μ t :

Viscosity of laminar and turbulent flow (N s/m2)

υ :

Kinematic viscosity (m2/s)

ε :

Dissipation rate of turbulent energy (m2/s2)

θ :

Angle of corregated plate

\( \bar{\sigma } \) :

Distance along the corrugated surface

σ ε , σ k , σ T :

k–ε Turbulence model constant for ε, k and T

ave:

Average

s :

Surface

in:

Inlet

w :

Wall

l :

Laminar

t :

Turbulent

out:

Outlet

References

  1. Dvorak FA (1969) Calculation of turbulent boundary layers on rough surfaces in pressure gradient. AIAA J 7:1752–1759

    Article  Google Scholar 

  2. Marriott J (1971) Where and how to use plate heat exchangers. Chem Eng 78:127–134

    Google Scholar 

  3. Sunden B, Skoldheden T (1985) Heat transfer and pressure drop in a new type of corrugated channels. Int Commun Heat Mass 12:559–566

    Article  Google Scholar 

  4. Webb BW, Ramadhyani S (1985) Conjugate heat transfer in a channel with staggered ribs. Int J Heat Mass Transfer 28:1679–1687

    Article  Google Scholar 

  5. Ghaddar NK, Karczak KZ, Mikic BB, Patera AT (1986) Numerical investigation of incompressible flow in grooved channels, part 1. Stability and self-sustained oscillations. J Fluid Mech 163:99–127

    Article  MathSciNet  Google Scholar 

  6. Focke WW, Knibbe PG (1986) Flow visualization in parallel-plate ducts with corrugated walls. J Fluid Mech 165:73–77

    Article  Google Scholar 

  7. Tachie MF, Shah MK (2008) Favorable pressure gradient turbulent flow over straight and inclined ribs on both channel walls. Phys Fluids 20:095103

    Article  Google Scholar 

  8. Brunner T, Brenig W (1988) Coupled channel calculations for the rotational excitation of molecules at corrugated surfaces. Surf Sci 201:321–334

    Article  Google Scholar 

  9. Mazouz A, Labraga L, Tournier C (1998) Anisotropy invariant of Reynolds stress tensor in a duct flow and turbulent boundary layer. J Fluids Eng 120:280

    Article  Google Scholar 

  10. Mulhearn PJ (1976) Turbulent boundary layer wall-pressure fluctuations downstream from an abrupt change in surface roughness. Phys Fluids 19:796

    Article  Google Scholar 

  11. Sunden B, Trollheden S (1989) Periodic laminar flow and heat transfer in a corrugated channel. Int Commun Heat Mass 16:215–225

    Article  Google Scholar 

  12. Bhaganagar K, Coleman G, Kim J (2007) Effect of roughness on pressure fluctuations in a turbulent channel flow. Phys Fluids 19:028103

    Article  Google Scholar 

  13. Amon CH, Mikic BB (1990) Numerical prediction of convective heat transfer in self-sustained oscillatory flows. J Thermophys Heat Transf 4:239–246

    Article  Google Scholar 

  14. Amon CH (1992) Heat transfer enhancement by flow destabilization in electronic chip configurations. ASME J Electron Packag 144:35–40

    Article  Google Scholar 

  15. Heavner RL, Kumar H, Wannizrachi AS (1993) Performance of an industrial plate heat exchanger: effect of chevron angle. AICHE Symp 89:65–70

    Google Scholar 

  16. Yalamanchili RC (1993) Flow of non-Newtonian fluids in corrugated channels. Int J Nonlinear Mech 28:535–548

    Article  Google Scholar 

  17. Yalamanchili RC, Sirivat A, Rajagopal KR (1995) An experimental investigation of the flow of dilute polymer solutions through corrugated channels. J Non-Newton Fluid 58:243–277

    Article  Google Scholar 

  18. Nikuradse J (1933) Laws of flow in rough pipes. NACA Technical Memorandum: 1292

  19. Ding J, Manglik RM (1996) Analytical solutions for laminar fully developed flows in double-sine shaped ducts. Heat Mass Transf 31:269–277

    Article  Google Scholar 

  20. Ciofalo M, Collins MW, Stasiek JA (1998) Flow and heat transfer predictions in flow passages of air preheaters: assessment of alternative modeling approaches. In: Sunden B, Faghri M (eds) Computer simulations in compact heat exchangers. Computational Mechanics Publications, UK, pp 169–225

    Google Scholar 

  21. Sawyer D, Sen M, Chang HC (1998) Heat transfer enhancement in three dimensional corrugated channel flow. Int J Heat Mass Transf 41:3559–3573

    Article  Google Scholar 

  22. Zimmerer C, Gschwind P, Gaiser G, Kottke V (2002) Comparison of heat and mass transfer in different heat exchanger geometries with corrugated walls. Exp Therm Fluid Sci 26:269–273

    Article  Google Scholar 

  23. Wang CC, Chen CK (2002) Forced convection in a wavy-wall channel. Int J Heat Mass Transf 45:2587–2595

    Article  MATH  Google Scholar 

  24. Karmare SV, Tikekar AN (2009) Experimental investigation of optimum thermohydraulic performance of solar air heaters with metal rib grits roughness. Sol Energy 83:6–13

    Article  Google Scholar 

  25. Dhananjay Gupta, Solanki SC, Saini JS (1997) Thermo hydraulic performance of solar air hearers with roughened absorber plates. Sol Energy 61:33–42

    Article  Google Scholar 

  26. Karwa R, Solanki SC, Saini JS (1999) Heat transfer coefficient and friction factor correlation for the transitional flow regime in rib roughened rectangular ducts. Int J Heat Mass Transf 42:1597–1615

    Article  Google Scholar 

  27. Nagano Y, Hattori H, Houra T (2004) DNS of velocity and thermal fields in turbulent channel flow with transverse-rib roughness. Int J Heat Fluid Flow 25:393–403

    Article  Google Scholar 

  28. Fabbri G, Rossi R (2005) Analysis of the heat transfer in the entrance region of optimized corrugated wall channel. Int Commun Heat Mass 32:902–912

    Article  Google Scholar 

  29. Naphon P (2007) Heat transfer characteristics and pressure drop in channel with V corrugated upper and lower plates. Energy Convers Manag 48:1516–1524

    Article  Google Scholar 

  30. Launder BE, Spalding DB (1972) The numerical computation of turbulent flow. Comput Methods Appl Mech Eng 3:269–289

    Article  Google Scholar 

  31. Kim SE, Choudhury D (1995) A near-wall treatment using wall functions sensitized to pressure gradient. Separated and Complex Flows ASME FED, vol 217, pp 273–279

  32. Webb RL (1994) Principles of enhanced heat transfer. Wiley, New York

    Google Scholar 

  33. Patankar SV (1980) Numerical heat transfer and fluid flow. McGraw-Hill, New York

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Cheng Kung University, Tainan, 70101, Taiwan

    Yue-Tzu Yang & Peng-Jen Chen

Authors
  1. Yue-Tzu Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Peng-Jen Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yue-Tzu Yang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, YT., Chen, PJ. Numerical simulation of fluid flow and heat transfer characteristics in channel with V corrugated plates. Heat Mass Transfer 46, 437–445 (2010). https://doi.org/10.1007/s00231-010-0586-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-010-0586-6

Keywords

Search

Navigation