1 Introduction

Problems of mass transfer at the fluid flow over a rotating disk for the Schmidt numbers greater than unity is of a great importance in a number of industrial and scientific applications. The main area of application for the present research is the naphthalene sublimation technique often employed in experimental measurements of the mass transfer coefficients h m [1–11].

Equations for the local and average Nusselt and Sherwood numbers can be written in the following generalized form [1–18]

$$ Nu = K_{1} Re^{{n_{{\text{R}}} }}_{\omega },\quad Nu_{{{\text{av}}}} = K_{2} Re^{{n_{{\text{R}}} }}_{\varphi }, $$
(1)
$$ Sh = K_{1} Re^{{n_{{\text{R}}} }}_{\omega },\quad Sh_{{{\text{av}}}} = K_{2} Re^{{n_{{\text{R}}} }}_{\varphi }, $$
(2)

where n R = 1/2 for laminar and, most often, n R = 0.8 for turbulent flows, while the constants K 1 and K 2 depend on the boundary conditions, flow regime and Pr or Sc numbers. The energy and diffusion equations, along with their boundary conditions T w = const or C w = const, are analogous, so that we will switch between their solutions (or experimental equations) throughout the paper simply substituting C, Sc and Sh instead of T, Pr and Nu (and vice versa), respectively.

There exists an analogy between the processes of convective heat transfer from a surface with surrounding air and mass transfer for naphthalene sublimation into air from the same surface. In the past, the naphthalene sublimation technique was used only to determine surface-averaged mass transfer of an entire disk by means of its weighing before and after the experiment and subsequent determination of the mass of naphthalene sublimated for the period of experiments [6–8, 10, 11]. At present, exact and reliable techniques are already available for the determination of not only surface-averaged, but also local mass transfer coefficients for laminar, transitional and turbulent flows at any point of the surface [1–5, 9].

The essence of the analogy between the processes of heat and mass transfer from a surface consists in the following. Relations for the coefficients K 1 in the equations for the Nusselt number (Eq. 1) and Sherwood number (Eq. 2) can be written as follows

$$ K_{1} = CPr^{{m_{{\text{p}}} }}, $$
(3)
$$ K_{1} = CSc^{{m_{{\text{p}}} }}, $$
(4)

where the constant С is the same for both equations, while the effect of the Prandtl and Schmidt numbers is taken into account by the respective factors in Eqs. (3) and (4).

1.1 Laminar flow

An application for the naphthalene sublimation technique means that Eqs. (3) and (4) will be used for the cases with the Pradntl and Schmidt numbers moderately less or larger than unity: Pr = 0.7…0.74 for heat transfer in air, and Sc = 2.28…2.5 for the naphthalene sublimation in air. Therefore, it is logical to assume that the coefficient С is equal to the constant K 1 at Sc = 1, Pr = 1 for the boundary conditions T w = const or C w = const [14]

$$ C = 0.3963. $$
(5)

In all the known applications of the naphthalene sublimation technique for the rotating disk problems [1–3, 5, 6, 9], it was assumed that the exponent m p is independent of the values of Pr and Sc, with the relation between the Nusselt and Sherwood numbers being written as

$$ Nu/Sh = (Pr/Sc)^{{m_{{\text{p}}} }} . $$
(6)

Different authors recommended various values of the exponent m p, which differ from each other by up to 45%. The values used were: m p = 1/3 [3]; m p = 0.4 [1, 2, 5, 7]; m p = 0.53 [6]; and m p = 0.58 [9].

A modification of Eq. (6) was offered in [10]

$$ Nu/Sh_{{{\text{Sc}} = 2.5}} = f(Pr)Pr^{{1/3}} . $$
(7)

This means that m p = 1/3, and all inaccuracies in the recalculation of the Nusselt number using the known value K 1 = 0.625 at Sc = 2.5 for the conditions at other Prandtl or Schmidt numbers should be corrected by means of the function f(Pr) = 0.576, 0.634, 0.737, 0.842 and 0.926 at Pr = 0.1, 1, 2.5, 10 and 100, respectively. As a result, K 1 = 0.321, 0.396, 0.625, 1.134 and 2.686 for the same Prandtl numbers. This coincides with the exact solution at T w = const.

It is obvious that an error in the choice of the value of m p can lead to significant errors in the recalculations of the data obtained using the naphthalene sublimation technique to the case of heat transfer in air. It is therefore necessary to analyze the values of m p suggested by different authors and develop recommendations regarding its most accurate value.

1.2 Turbulent flow

Experimental data for the local coefficients of mass transfer for naphthalene sublimation from a surface of a rotating disk in transitional and turbulent flow regimes were apparently for the first time obtained in the resent investigations [1, 5] (Fig. 1).

Fig. 1
figure 1

Local Sherwood numbers for naphthalene sublimation in air. Experiments: 1, Sc = 2.28 [1]; 2, Sc = 2.4 [8]; 3, Sc = 2.4 [11]; 4, Sc = 2.44 [6]; 5, Sc not mentioned [5]. Empirical approximations of the experiments with the help of Eq. (2): 6, laminar flow, n R  = 1/2, K 1 = 0.625 [7, 8, 10, 11]; 7, laminar flow, n R  = 1/2, K 1 = 0.604 [3]; 8, transitional flow, n R  = 4, K 1 = 2·10−19 (Eq. 8) [1]; 9, turbulent flow, n R  = 0.8, K 1 = 0.0512 (Eq. 9) [1]

Full size image

Authors [1, 5] developed approximations of their experimental data

$$ Sh = 2.0 \cdot 10^{{ - 19}} \cdot Re^{4}_{\omega } \quad {\text{for }}Re_{\omega } = (1.9 \ldots 2.75) \cdot 10^{5}, [1], $$
(8)
$$ Sh = 0.0512Re^{{0.8}}_{\omega } \quad {\text{for}}\;Re_{\omega } \ge 2.75 \cdot 10^{5}, [1], $$
(9)
$$Sh = 0.0518Re^{{0.8}}_{\omega } \quad {\text{for }}Re_{\omega } \ge 2.5 \cdot 10^{5}, [5], $$
(10)

where Eq. (8) is valid for transitional flows, and Eqs. (9), (10) relate to turbulent flows.

Authors of works [6–8, 10, 11] obtained experimental data for the average Sherwood number of the entire disk where regions of laminar, transitional and turbulent flows existed simultaneously. In order to obtain a relation for Sh av for the entire disk, authors of papers [8, 11] used an approach based on the Reynolds analogy between the processes of heat (and mass) transfer and fluid flow. Equations for the Nusselt and Sherwood number obtained as a result are inconvenient and contain parameters, whose determination in frames of the model used was quite complicated. The application of the Reynolds analogy seems to be forced by the lack of experimental data for the local Sherwood numbers that could have been used for constructing models for Sh av for the entire disk in a more direct way. Model [19] for Sh av used in electrochemical applications and considered in detail in Sect. 3 looks much more justifiable. An extension of this model to the mass transfer for naphthalene sublimation is important, because it can allow validations of the relatively recent data for the local values of the Sherwood numbers via comparisons with the huge massive of data for Sh av available for the entire disk.

Like at the laminar regime of flow, the recalculation of the data for mass transfer to the respective relations for heat transfer is based on Eq. (1) for the Nusselt number and Eq. (2) for Sherwood number, with coefficients K 1 in these equations being written as Eqs. (3) and (4), respectively. In doing so, factort С is considered to be equal to the value of K 1 at Sc = 1, Pr = 1 for the boundary conditions T w = const or C w = const.

In fact, authors [1, 5] assumed that, over the range Pr = Sc = 0.7 to 2.5, the exponent m p is constant also for the turbulent flow and equals to m p = 0.4. This assumption was made based on the recommendations of [2]. As far as we know, no other author developed any recommendation regarding the value of m p for the transitional and turbulent flows. Applying the value m p = 0.4 to Eq. (6), using Eq. (9) for the Sherwood number at Sc = 2.28 and calculating finally the coefficient K 1 for air at Pr = 0.72, one can obtain that the value K 1 at T w = const should be equal to K 1 = 0.0323. However, in the reality, at T w = const and Pr = 0.72, the coefficient K 1 is equal to 0.0188 according to experiments [15, 16] or to 0.0187 based on the theoretical model [17, 18].

So, it is again obvious also for the turbulent flow that the aforementioned error in the choice of the value of m p leads to the significant error in the recalculation of the data from the naphthalene sublimation technique to the case of heat transfer in air.

Thus, the objectives of the present research were: (a) to fulfill a comprehensive analysis and a validation of the available experimental data for the naphthalene sublimation in air; (b) to validate relations connecting local and average Sherwood numbers for the entire disk; (c) to develop recommendations regarding the most accurate correlations for the recalculation of the experimental data on mass transfer for naphthalene sublimation in air to the relations for heat transfer of a rotating disk in air.

2 Naphthalene sublimation technique at laminar flow

The values of the exponent m p can be determined from the exact solution of the system of the Navier-Stokes and thermal boundary layer equations in a self-similar form [12–14]. The data for m p for a series of the discrete values of the Prandtl (or Schmidt) numbers moderately different from unity are given in Table 1. One can conclude from these results that the exponent m p decreases from the value m p = 0.5723 to m p = 0.5024 with the Prandtl or Schmidt numbers increasing from 0.7 to 2.5. Thus, the value m p = 0.53 offered in [6] is, in fact, the average over the range of its variation with the Prandtl numbers varying from Pr = 0.7 to 2.5.

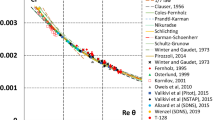
Table 1 Value m p in Eqs. (3), (4) and (6) based on the exact solution for laminar flow [12–14]
Full size table

Experimental data of different authors for the coefficient K 1 for naphthalene sublimation in air are given in Fig. 2 and explained in detail in its caption. In general, these data agree well with the results of the exact solution, which predict values K 1 = 0.6016, 0.6162 and 0.628 for Sc = 2.28, 2.4 and 2.5, the range mentioned in experimental studies. Having recalculated the experimental data with the help of Eq. (6) at m p = 0.53 to the case of Pr = 0.71, one can obtain: K 1 = 0.318 [1]; K 1 = 0.325 [3]; K 1 = 0.328 [7, 8, 11]; K 1 = 0.331 [6]; K 1 = 0.321 [10]; K 1 = 0.354 [9]. Thus, data [3, 6–8, 10, 11] are in the excellent agreement with the exact solution K 1 = 0.326 for Pr = 0.71 and T w = const [13, 14] and experimental data on heat transfer in these conditions (see review work [13]). The value K 1 = 0.318 [1] is somewhat lower than the data of other authors, and the reason lies probably in the somewhat lower value K 1 = 0.59 obtained in [1] for naphthalene sublimation at Sc = 2.28. The value K 1 = 0.354 [9] is too high, because the experimental value K 1 = 0.69 of these authors for naphthalene sublimation is also too high (see also Fig. 2).

Fig. 2
figure 2

Coefficient K 1 in Eq. (2), laminar flow at C w  = const. Experiments: 1, K 1 = 0.59, Sc = 2.28 [1]; 2, K 1 = 0.604, Sc = 2.28 [3]; 3, K 1 = 0.625, Sc = 2.4 [7, 8, 11]; 4, K 1 = 0.636, Sc = 2.44 [6]; 5, K 1 = 0.625, Sc = 2.5 [10]; 6, K 1 = 0.69, Sc = 2.5 [9]

Full size image

With the value m p = 0.4 recommended in [1, 3, 5, 7], one can obtain for the conditions at Pr = 0.71: K 1 = 0.37 [1]; K 1 = 0.379 [3]; K 1 = 0.384 [7, 8, 11]; K 1 = 0.388 [6]; K 1 = 0.378 [10]; K 1 = 0.417 [9]. These values of the coefficient K 1 are too high in comparison with the exact solution K 1 = 0.326. It is especially important to accentuate this, because the experimental results [1, 3, 5] obtained relatively recently are accurate in the part of mass transfer data.

For the value m p = 1/3 recommended in [3] one can obtain data K 1 for Pr = 0.71 that are even more overestimated in comparison with the exact solution.

Authors of the work [9] suggested the value m p = 0.58. In this case one can obtain for Pr = 0.71: K 1 = 0.3 [1]; K 1 = 0.307 [3]; K 1 = 0.308 [7, 8, 11]; K 1 = 0.311 [6]; K 1 = 0.301 [10]; K 1 = 0.332 [9]. Hence, all the values of K 1 recalculated to the case Pr = 0.71 are too low in comparison with the exact solution except for the data [9]. Apparently, authors of the work [9] had to choose such a high value of m p in order to obtain the recalculated coefficient K 1 agreeing well with the data for heat transfer at Pr = 0.71. It is obvious, however, that the problem is that the value K 1 = 0.69 obtained in [9] for naphthalene sublimation is too high and disagree with the numerous data of the other researchers.

In the approach based on Eq. (7), the factor Pr 1/3 is in principle redundant, because the correction function f(Pr) can be tabulated via a computation of the ratio Nu/Sh Sc=2.5 with the help of the exact solution over any range of Pr and Sc. An advantage of such a method is its higher accuracy and universality, while the disadvantage of Eq. (7) is its poorer obviousness, because a tabulated function is always less convenient than an accurate approximating formula.

Thus, for the recalculation of the data for laminar mass transfer from a rotating disk for naphthalene sublimation in air to the case of laminar heat transfer in air, one can recommend to use Eq. (6) at the value of the power exponent m p = 0.53 offered in [6], or, alternatively, Eq. (7) (or its modification) with the appropriately tabulated function f(Pr).

3 Comparative analysis of the experimental data for the Sherwood number for transitional and turbulent flows

As mentioned above, the development of the relation for the average Sherwood number for the entire disk will be grounded on the approach formulated in [19]. The author [19] assumed that at simultaneous existence of the regions of laminar, transitional and turbulent flows on the disk, the span of the transitional zone is rather small, and the transition from laminar to turbulent flow occurs abruptly at the radial location r tr for the Reynolds number Re ω,tr. Then the integration in order to obtain the value Sh av for the entire disk should be done as

$$ Sh_{{{\text{av}}}} = \frac{2} {b}{\left[ {{\int\limits_0^{r_{{{\text{tr}}}} } {Sh_{{{\text{lam}}}} dr + {\int\limits_{r_{{{\text{tr}}}} }^b {Sh_{{{\text{turb}}}} dr} }} }} \right]}. $$
(11)

The Sherwood numbers are defined in Eq. (2); the allowance should be made for the real values K 1,lam and n R = 1/2 for the laminar flow (subscript “lam”), and K 1,turb and n R = 0.8 for the turbulent flow (subscript “turb”).

As a result of the integration of Eq. (11), one can obtain

$$ Sh_{{{\text{av}}}} = K_{{1,{\text{lam}}}} Re^{{1/2}}_{{\omega,{\text{tr}}}} {\left( {\frac{{Re_{{\omega,{\text{tr}}}} }} {{Re_{\varphi } }}} \right)}^{{1/2}} + \frac{2} {{2n_{{\text{R}}} + 1}}K_{{1,{\text{turb}}}} Re^{{n_{{\text{R}}} }}_{\varphi } {\left[ {1 - {\left( {\frac{{Re_{{\omega,{\text{tr}}}} }} {{Re_{\varphi } }}} \right)}^{{n_{{\text{R}}} + 1/2}} } \right]}. $$
(12)

Equation (12) is valid for \( Re_{\varphi } \ge Re_{{\omega,{\text{tr}}}} . \) If \( Re_{\varphi } < Re_{{\omega,{\text{tr}}}}, \) the second term in Eq. (12) should be neglected. In the limiting case \( Re_{\varphi } \gg Re_{{\omega,{\text{tr}}}}, \) Eq. (12) reduces to the second of Eq. (2) for developed turbulent flow existing over the entire disk surface, where

$$ K_{{2,{\text{turb}}}} = \frac{2} {{2n_{{\text{R}}} + 1}}K_{{1,{\text{turb}}}} . $$
(13)

The model of [19] can be generalized taking into account every region of the laminar, transitional and turbulent flows separately as suggested in [20]. Assuming that the transition starts at the radial coordinate r tr1 for the Reynolds number Re ω,tr1, while the end of the transition takes place at the radial coordinate r tr2 for the Reynolds number Re ω,tr2, then the integration to find Sh av should be performed as follows

$$ Sh_{{{\text{av}}}} = \frac{2} {b}{\left[ {{\int\limits_0^{r_{{{\text{tr}}1}} } {Sh_{{{\text{lam}}}} dr + {\int\limits_{r_{{{\text{tr}}1}} }^{r_{{{\text{tr}}2}} } {Sh_{{{\text{tran}}}} dr} } + {\int\limits_{r_{{{\text{tr}}2}} }^b {Sh_{{{\text{turb}}}} dr} }} }} \right]}. $$
(14)

Newly introduced function Sh tran is defined by Eq. (2) with allowance for experimentally determined values of K 1,tran и n R,tran for transitional flow (subscript “tran”).

As a result of the integration of Eq. (14), one can obtain

$$ \begin{aligned}{} Sh_{{{\text{av}}}} & = K_{{1,{\text{lam}}}} Re^{{1/2}}_{{\omega,{\text{tr}}1}} {\left( {\frac{{Re_{{\omega,{\text{tr}}1}} }} {{Re_{\varphi } }}} \right)}^{{1/2}} + \frac{2} {{2n_{{{\text{R}},{\text{tran}}}} + 1}}K_{{1,{\text{tran}}}} Re^{{n_{{{\text{R}},{\text{tran}}}} }}_{{\omega,{\text{tr}}2}} {\left( {\frac{{Re_{{\omega,{\text{tr}}2}} }} {{Re_{\varphi } }}} \right)}^{{1/2}} {\left[ {1 - {\left( {\frac{{Re_{{\omega,{\text{tr}}1}} }} {{Re_{{\omega,{\text{tr}}2}} }}} \right)}^{{n_{{{\text{R}},{\text{tran}}}} + 1/2}} } \right]} \\ & \quad + \frac{2} {{2n_{{\text{R}}} + 1}}K_{{1,{\text{turb}}}} Re^{{n_{{\text{R}}} }}_{\varphi } {\left[ {1 - {\left( {\frac{{Re_{{\omega,{\text{tr}}2}} }} {{Re_{\varphi } }}} \right)}^{{n_{{\text{R}}} + 1/2}} } \right]}. \\ \end{aligned} $$
(15)

Equation (15) is applicable for \( Re_{\varphi } \ge Re_{{\omega,{\text{tr2}}}} . \) If \( Re_{\varphi } < Re_{{\omega,{\text{tr2}}}}, \) the third term in Eq. (15) should be neglected, with the second term taking a simpler form

$$ Sh_{{{\text{av}}}} = K_{{1,{\text{lam}}}} Re^{{1/2}}_{{\omega,{\text{tr1}}}} {\left( {\frac{{Re_{{\omega,{\text{tr1}}}} }} {{Re_{\varphi } }}} \right)}^{{{\text{1/2}}}} + \frac{2} {{2n_{{{\text{R}},{\text{tran}}}} + 1}}K_{{1,{\text{tran}}}} Re^{{n_{{{\text{R}},{\text{tran}}}} }}_{\varphi } {\left[ {1 - {\left( {\frac{{Re_{{\omega ,{\text{tr1}}}} }} {{Re_{\varphi } }}} \right)}^{{n_{{{\text{R}},{\text{tran}}}} + {\text{1/2}}}} } \right]}. $$
(16)

In the limiting case of \( Re_{\varphi } \gg Re_{{\omega ,{\text{tr}}2}} , \) Eq. (15) reduces to the second of Eq. (2) with K 2,turb given in Eq. (13).

Mohr and Newman [20], while determining the average Sherwood number for the entire disk, derived an expression that is a particular case of Eq. (15), because it already contains numerical values of all the empirical constants obtained in experiments [20] (electrochemical applications at high Schmidt numbers). Because of this, expression [20] cannot be directly applied for the case of naphthalene sublimation in air.

In order to make comparisons with the experimental data for Sh av, let us substitute numerical values of the constants obtained in [1] (see Eqs. (8), (9), and caption to Fig. 2) into the general equations derived above. As a result, one can obtain from Eqs. (12), (13), (15) and (16), respectively

$$ Sh_{{{\text{av}}}} = 0.59Re^{{1/2}}_{{\omega ,{\text{tr}}}} {\left( {\frac{{Re_{{\omega ,{\text{tr}}}} }} {{Re_{\varphi } }}} \right)}^{{1/2}} + \frac{2} {{2.6}}0.512Re^{{0.8}}_{\varphi } {\left[ {1 - {\left( {\frac{{Re_{{\omega ,{\text{tr}}}} }} {{Re_{\varphi } }}} \right)}^{{1.3}} } \right]}, $$
(17)
$$ K_{{2,{\text{turb}}}} = \frac{2} {{2.6}}K_{{1,{\text{turb}}}} = 0.0394, $$
(18)
$$ \begin{aligned}{} Sh_{{{\text{av}}}} & = 0.59 \cdot 1.9 \cdot 10^{5} \cdot Re^{{ - 1/2}}_{\varphi } +\, \frac{4} {9}10^{{ - 19}} (2.75 \cdot 10^{5} )^{{4.5}} Re^{{ - 1/2}}_{\varphi } {\left[ {1 - {\left( {\frac{{1.9 \cdot 10^{5} }} {{2.75 \cdot 10^{5} }}} \right)}^{{4.5}} } \right]} \\ & \quad +\,0.0394Re^{{0.8}}_{\varphi } {\left[ {1 - {\left( {\frac{{2.75 \cdot 10^{5} }} {{Re_{\varphi } }}} \right)}^{{1.3}} } \right]},\quad Re_{\varphi } \ge {\text{ }}2.75 \cdot 10^{5} ,{\text{ }} \\ \end{aligned} $$
(19)
$$ Sh_{{{\text{av}}}} = 0.59 \cdot 1.9 \cdot 10^{5} \cdot Re^{{ - 1/2}}_{\varphi } + \frac{4} {9}10^{{ - 19}} Re^{4}_{\varphi } {\left[ {1 - {\left( {\frac{{1.9 \cdot 10^{5} }} {{Re_{\varphi } }}} \right)}^{{4.5}} } \right]},{\text{ }}Re_{\varphi } = (1.9 \ldots 2.75) \cdot 10^{5} . $$
(20)

The Reynolds number of the abrupt transition to turbulent flow Re ω,tr in Eq. (17) was left as a unknown parameter that can be varied to reach a better agreement with the experiments.

A comparison of Eqs. (17)–(20) with experimental data of different authors is presented in Fig. 3. Experimental data 1, 5 and curve 6 for Sh av for developed turbulent flow were obtained in the present work by means of a recalculation of the experimental data [1, 5] and Eq. (9) with the help of Eq. (18). It should be remembered also that for laminar flow K 2,lam = K 1,lam (curves 7 and 8). Curve 9, computed via combining Eqs. (19) and (20) and taking into account boundaries of the beginning and end of the transition to the turbulent flow, agrees well with the experimental data [6, 8, 11] for Sh av for the entire disk presented in Fig. 3.

Fig. 3
figure 3

Average Sherwood numbers for naphthalene sublimation in air. Experiments: 1, Sc = 2.28 [1]; 2, Sc = 2.4 [8]; 3, Sc = 2.4 [11]; 4, Sc = 2.44 [6]; 5, Sc not mentioned [5]. Calculation based on Eq. (2): 6, turbulent flow region, n R  = 0.8, K 2 = 0.0394 (Eq. 18) [1]; 7, laminar flow, n R  = 1/2, K 1 = 0.625 [7, 8, 10, 11]; 8, laminar flow, n R  = 1/2, K 1 = 0.59 [1]. Calculation of Sh av for the entire disk: 9, Eqs. (19) and (20); 10, Eq. (17) at Re ω,tr = 1.9·105; 11, Eq. (17) at Re ω,tr = 2.75·105; 12, Eq. (17) at Re ω,tr = 2.35·105

Full size image

Experimental points 1 for Sh av for the entire disk presented in Fig. 3 were computed in the present work based on the data [1] for laminar, transitional and turbulent flow with the help of Eqs. (19) and (20). It is obvious that these points coincide with curve 9 for the correspondent values of the Reynolds number.

Substituting the Reynolds numbers on the lower and upper border of the transitional region (i.e. 1.9·105 and 2.75·105, respectively) as Re ω,tr in Eq. (17) (abrupt transition to turbulent flow) resulted in curves 10 and 11, which lie higher and lower than curve 9, respectively. In order to agree with curve 9, one should choose an average (or “effective”) Reynolds number of the abrupt transition to turbulent flow, which in this case is equal to Re ω,tr = 2.35·105 (curve 12). This effective Reynolds number Re ω,tr is, in fact, the arithmetic mean of the Reynolds numbers of the beginning Re ω,tr1 and end Re ω,tr2 of the transition to turbulent flow.

It should be pointed out that all curves 9–12 in the limiting case of Re φ→∞ merge with curve 6 for the developed turbulent flow over the entire disk.

Thus, Eqs. (15) and (16), based on the model taking into account simultaneous existence of the regions of laminar, transitional and turbulent flows, provide the highest accuracy in predicting the average Sherwood numbers for the entire disk. The simpler Eq. (12), based on the model [19], also provides the accuracy comparable with that of Eqs. (15) and (16) under the condition of correct determining the “effective” Reynolds number Re ω,tr of the abrupt transition to turbulent flow. One should also point out that the conditions of the beginning and the end of the transition to turbulent flow are different in experiments of different authors, therefore, the “effective” value Re ω,tr should be found out individually in every case.

4 Naphthalene sublimation technique for transitional and turbulent flows

As mentioned in Introduction, the coefficient С in Eqs. (3) and (4) should be equal to the value of K 1 for the turbulent regime at Sc = 1, Pr = 1 for the boundary conditions T w = const or C w = const. Thus, according to [12, 13, 17, 18]

$$ C = 0.0232. $$
(21)

Contrary to the laminar flow case, an exact self-similar solution for the turbulent flow regime does not exist at all. Hence, a determination of the exponent m p should be based on experimental data. In fact, only experiments [1, 5] for naphthalene sublimation and their approximations in the form of Eqs. (9) and (10) are available for this purpose. In view of Eqs. (9), (21), and value K 1 = 0.0188 at T w = const and Pr = 0.72, Eqs. (3) and (4) take the following form

$$ K_{1} = 0.0232Pr^{{0.64}} \quad {\text{for }}Pr \le 1, $$
(22)
$$ K_{1} = 0.0232Sc^{{0.96}} \quad {\text{for }}Sc \ge 1. $$
(23)

Thus, the exponent m p for turbulent flow varies significantly depending on the Prandtl and Schmidt numbers. The relation between the Nusselt number for heat transfer in air and Sherwood number for naphthalene sublimation in air looks therefore as follows

$$ Nu/Sh = Pr^{{0.64}} /Sc^{{0.96}} . $$
(24)

As a development of the idea [10] expressed in Eq. (7), one can rewrite Eq. (24) as

$$ Nu/Sh_{{Sc = 2.28}} = f(Pr), $$
(25)

where the correction function f(Pr) is equal to 0.367 at Pr = 0.72.

Finally, in analogy to laminar flow, one can choose an effective value of m p that allows using the relation between Nu and Sh in the form of Eq. (6)

$$ Nu/Sh = (Pr/Sc)^{{0.87}} . $$
(26)

The value of m p in Eq. (26) is more than twice as high as the value 0.4 erroneously recommended in [1, 5]. One should remember, however, that the value m p = 0.87 must not be used in Eqs. (22) and (23), because this can cause significant errors in the calculations of the coefficient K 1.

An analysis for the transitional flow shows that the empirical equation of the authors [16] for T w = const and Pr = 0.72

$$ Nu = 10.0 \cdot 10^{{ - 20}} \cdot Re^{4}_{\omega } {\text{ for }}Re_{\omega } = (1.95 \ldots 2.5) \cdot 10^{5} , $$
(27)

fits in the best way to compare with the case of C w = const considered here. For transitional flow, Eq. (26) should be modified with allowance for Eqs. (27) and (8) in the following way

$$ Nu/Sh = (Pr/Sc)^{{0.6}} . $$
(28)

The range of validity of Eq. (27) is somewhat narrower in comparison with that of Eq. (8), where Re ω = (1.9–2.75)·105. However, this difference is rather small.

Thus, in order to recalculate the data for turbulent mass transfer for naphthalene sublimation from a disk to air to the case of heat transfer with air, one can recommend using any of the Eqs. (24)–(26), while for transitional flow Eq. (28) should be applied.

5 Conclusions

Experimental data available for mass transfer for naphthalene sublimation in the transitional and turbulent flows were analyzed, the relations connecting the local and average Sherwood numbers (including those for the entire disk where laminar, transitional and turbulent regions coexist simultaneously) were thoroughly validated. For the recalculation of the experimental data on the mass transfer for naphthalene sublimation in air to the relations for heat transfer in air, recommendations regarding the most accurate correlations for laminar flow (out of the existing ones) and new original relations for transitional and turbulent flows were developed.