Skip to main content
SpringerLink
Log in

Unsteady free convection flow over an infinite vertical porous plate due to the combined effects of thermal and mass diffusion, magnetic field and Hall currents

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

Abstract.

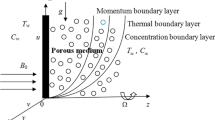
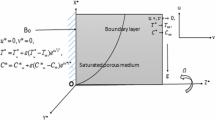
The unsteady free convection flow over an infinite vertical porous plate, which moves with time-dependent velocity in an ambient fluid, has been studied. The effects of the magnetic field and Hall current are included in the analysis. The buoyancy forces arise due to both the thermal and mass diffusion. The partial differential equations governing the flow have been solved numerically using both the implicit finite difference scheme and the difference-differential method. For the steady case, analytical solutions have also been obtained. The effect of time variation on the skin friction, heat transfer and mass transfer is very significant. Suction increases the skin friction coefficient in the primary flow, and also the Nusselt and Sherwood numbers, but the skin friction coefficient in the secondary flow is reduced. The effect of injection is opposite to that of suction. The buoyancy force, injection and the Hall parameter induce an overshoot in the velocity profiles in the primary flow which changes the velocity gradient from a negative to a positive value, but the magnetic field and suction reduce this velocity overshoot.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.
Fig. 11.
Fig. 12.

Similar content being viewed by others

References

  1. Ede AJ (1967) Advances in heat transfer. Academic Press, New York 4: 1–64

    Google Scholar 

  2. Gebhart B (1973) Advances in heat transfer. Academic Press, New York 9: 273–348

    Google Scholar 

  3. Jaluria Y (1980) Natural convection heat and mass transfer. Pergamon Press, Oxford

  4. Raithby GD; Hollands KGT (1985) Natural convection. In: Rohsenow WM et al (ed) Handbook of heat transfer fundamentals 2nd. Ed McGraw Hill, New York

  5. Gebhart B; Jaluria Y; Mahajan L; Sammakia B (1989) Buoyancy induced flows and transport. Hemisphere, publishing corporation, Washington DC

  6. Gupta AS (1960) Steady and transient free convection of an electrically conducting fluid from a vertical plate in the presence of a magnetic field. Appl Sci Res A9: 319–333

    Google Scholar 

  7. Osterle JF; Young FJ (1961) Natural convection between heated vertical plates in a horizontal magnetic field. J Fluid Mech 11: 512–518

    Google Scholar 

  8. Sparrow EM; Cess RD (1961) The effect of a magnetic field in free convection heat transfer. Int J Heat Mass Transfer 3: 267–274

    Article  Google Scholar 

  9. Gupta AS (1962) Laminar free convection flow of an electrically conducting fluid from a vertical plate with uniform surface heat flux and variable wall temperature in the presence of a magnetic field. ZAMP 13: 324–333

    Google Scholar 

  10. Cramer KR (1963) Several magnetohydrodynamic free convection solutions. J Heat Transfer 85: 35–40

    Google Scholar 

  11. Singh KR; Cowling TG (1963) Thermal convection in magnetohydrodynamics, 1. Boundary layer flow on a hot vertical plate. Q J Mech Appl Math 16: 1–15

    Google Scholar 

  12. Pop I (1969) On the unsteady hydromagnetic free convection flow past a vertical infinite flat plate. Indian J Phys 43: 196–200

    Google Scholar 

  13. Takhar HS (1971) Hydromagnetic free convection from a flat plate. Indian J Phys 45: 289–311

    Google Scholar 

  14. Katagiri M (1969) The effect of Hall current in the MHD boundary layer flow past a semi-infinite plate. J Phys Soc Jpn 27: 1051–1059

    Google Scholar 

  15. Kuiken HK (1970) Magnetohydrodynamic free convection in a strong cross field. J Fluid Mech 40: 1–15

    Google Scholar 

  16. Blums EJ; Fedin AG (1971) Non-stationary MHD free convection on a vertical plate. Izv AN Latv, SSR, Ser fiz, i tech-nauk 1: 65–75

    Google Scholar 

  17. Graham W (1976) Magnetohydrodynamic free convection about a semi-infinite vertical plate in a strong cross field. ZAMP 27: 621–631

    Google Scholar 

  18. Tokis JN; Pande GC (1981) Unsteady hydromagnetic flow near a moving porous plate. J Appl Mech 48: 255–272

    Google Scholar 

  19. Hossain MA (1986) Effect of Hall current on unsteady hydromagnetic free convection flow near an infinite vertical porous plate. J Phys Soc Jpn 55: 2183–2190

    Google Scholar 

  20. Hossain MA; Rashid R (1987) Hall effects on hydromagnetic free convection flow along a porous flat plate with mass transfer. J Physical Soc Jpn 56: 97–104

    CAS  Google Scholar 

  21. Acharya M; Dash GC; Singh LP (1995) Effect of chemical or thermal diffusion with Hall current on unsteady hydromagnetic flow near an infinite vertical porous plate. J Physics-D Appl Phy 28: 2455–2464

    Article  CAS  Google Scholar 

  22. Chamkha AJ (1997) Hydromagnetic natural convection flow on isothermal inclined surface adjacent to a thermally stratified porous medium. Int J Engng Sci 35: 975–986

    Article  CAS  Google Scholar 

  23. Minto BJ; Ingham DB; Pop I (1998) Free convection driven by an exothermic reaction on a vertical surface embedded in porous media. Int J Heat Mass Transfer 41: 11–24

    Article  CAS  Google Scholar 

  24. Yih KA (1999) Uniform transpiration effect in the combined heat and mass transfer by natural convection over a cone in saturated porous media: uniform wall temperature/concentration or heat/mass flux. Int J Heat Mass Transfer 42: 3533–3537

    Article  Google Scholar 

  25. Rees DAS; Pop I (2000) Vertical free convection in a porous medium with variable permeability effect. Int J Engng Sci 38: 2565–2572

    Google Scholar 

  26. Eringen AC; Maugin GA (1990) Electrodynamics of Continua. Vol. 2, Springer Verlag, Berlin, Germany

  27. Roache PJ (1982) Computational Fluid Dynamics. Hermosa, Albuquerque, NM, USA

  28. Varga RS (1962) Matrix Iterative Analysis. Prentice Hall, New Jersey, USA, p 194

  29. Jaffe NA; Smith AMO (1972) Calculation of laminar boundary layers by means of a differential-difference method. Progress in Aerospace Sciences, Pergamon Press, New York, USA

  30. Na TY (1979) Computational Methods in Engineering Boundary Value Problems. Academic Press, New York, USA

  31. Chen TS; Strobel FA (1980) Buoyancy effects in boundary layer adjacent to a continuous moving horizontal flat plate. J Heat Trans 102: 170–172

    CAS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering, Manchester Metropolitan University, Manchester, M1 5GD, UK

    H. S. Takhar

  2. Department of Mathematics, Indian Institute of Technology Madras, Chenai – 600036, India

    S. Roy

  3. Department of Mathematics, Indian Institute of Science, Bangalore – 560 0112 , India

    G. Nath

Authors
  1. H. S. Takhar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Roy
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G. Nath
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. S. Takhar.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Takhar, H.S., Roy, S. & Nath, G. Unsteady free convection flow over an infinite vertical porous plate due to the combined effects of thermal and mass diffusion, magnetic field and Hall currents. Heat and Mass Transfer 39, 825–834 (2003). https://doi.org/10.1007/s00231-003-0427-y

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-003-0427-y

Keywords

Search

Navigation