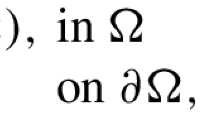Abstract
This paper deals with global integrability for solutions to quasilinear elliptic systems involving N equations of the form
where \(\alpha \in \{1,\ldots ,N\}\) is the equation index, \(\Omega \) is an open bounded subset of \({\mathbb {R}}^n\), \(n>2\), \(u=(u^1,\ldots ,u^N): \Omega \rightarrow {\mathbb {R}}^N\) and \(f\in L^m(\Omega ), \frac{2n}{n+2}\le m\le \frac{n}{2}\). Under ellipticity condition of diagonal coefficients, smallness and staircase support conditions of off-diagonal coefficients, we derive some global integrability results.
Similar content being viewed by others
References
Boccardo, L.: Problemi differenziali ellittici e parabolici con dati misure. Boll. Unione Mat. Ital. Sez. A 11, 439–461 (1997)
Baroni, P.: Riesz potential estimates for a general class of quasilinear equations. Calc. Var. Partial Differ. Equ. 53, 803–846 (2015)
Benilan, P., Boccardo, L., Gallouët, T., Gariepy, R., Pierre, M., Vazquez, J.L.: An \(L^1\) theory of existence and uniqueness of nonlinear elliptic equations. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 22, 240–273 (1995)
Boccardo, L., Croce, G.: Elliptic Partial Differential Equations, De Gruyter Studies in Mathematics, vol. 55. De Gruyter, Berlin (2014)
Boccardo, L., Croce, G.: Esistenza e regolarità di soluzioni di alcuni problemi ellittici, In: Quaderni dell\(^{\prime }\)UMI, vol. 51, Pitagora Editrice, Bologna (2010)
Boccardo, L., Cirmi, G.R.: Existence and uniqueness of solution of unilateral problems with \(L^1\) data. J. Convex Anal. 6, 195–206 (1999)
Boccardo, L., Dall’Aglio, A., Orsina, L.: Existence and regularity results for some elliptic equations with degenerate coercivity. Atti Sem. Mat. Fis. Univ. Modena. 46, 51–81 (1998)
Boccardo, L., Gallouët, T.: Nonlinear elliptic and parabolic equations involving measure data. J. Funct. Anal. 87, 149–169 (1989)
Boccardo, L., Gallouët, T., Orsina, L.: Existence and uniqueness of entropy solutions for nonlinear elliptic equations with measure data. Ann. Inst. H. Poincaré Anal. Non Linéaire 13, 539–551 (1996)
Betta, M.F., Del Vecchio, T., Posteraro, M.R.: Existence and regularity results for nonlinear degenerate elliptic equations with measure data. Ric. Mat. 47, 277–295 (1998)
Boccardo, L., Gallouët, T., Marcellini, P.: Anisotropic equations in \(L^1\). Differ. Integral Equ. 9, 209–212 (1996)
Cirmi, G.R.: On the existence of solutions to nonlinear degenerate elliptic equations with measure data. Ric. Mat. 42, 315–329 (1993)
Cirmi, G.R., Leonardi, S.: Regularity results for the gradient of solutions linear elliptic equations with \(L^{1,\lambda }\) data. Ann. Mat. Pura Appl. 185, 537–553 (2006)
Dall’Aglio, A.: Approximated solutions of equations with \(L^1\) data. Application to the \(H\)-convergence of quasi-linear parabolic equations. Ann. Mat. Pura Appl 170, 207–240 (1996)
Dolzmann, G., Hungerbühler, N., Müller, S.: The \(p\)-harmonic systems with measure-valued right hand side. Ann. Inst. H. Poincaré Anal. Non Linéaire 14, 353–364 (1997)
Fuchs, M., Reuling, J.: Non-linear elliptic systems involving measure data. Rend. Mat. Appl. 15, 101–109 (1995)
Gao, H., Liang, S., Cui, Y.: Regularity for anisotropic solutions to some nonlinear elliptic system. Front. Math. China 11, 77–87 (2016)
Gao, H., Leonetti, F., Ren, W.: Regularity for anisotropic elliptic equations with degenerate coercivity. Nonlinear Anal. 187, 493–505 (2019)
Kovalevskii, A.A.: On the summability of entropy solutions for the Dirichlet problem in a class of non-linear elliptic fourth-order equations. Izv. Math. 67, 881–894 (2003)
Kuusi, T., Mingione, G.: Universal potential estimates. J. Funct. Anal. 262, 4205–4269 (2012)
Leonardi, S., Leonetti, F., Pignotti, C., Rocha, E., Staicu, V.: Maximum principles for some quasilinear elliptic systems. Nonlinear Anal. https://doi.org/10.1016/j.na.2018.11.004
Leone, C., Porretta, A.: Entropy solutions to nonlinear elliptic equations in \(L^1\). Nonlinear Anal. 32, 325–334 (1998)
Leonetti, F., Petricca, P.V.: Anisotropic elliptic systems with measure data. Ric. Mat. 54, 591–595 (2005)
Leonetti, F., Petricca, P.V.: Existence for some vectorial elliptic problems with measure data. Riv. Math. Univ. Parma 5, 33–46 (2006)
Leonetti, F., Petricca, P.V.: Existence of bounded solutions to some nonlinear degenerate elliptic systems. Discrete Contin. Dyn. Syst, Ser B 11, 191–203 (2009)
Leonetti, F., Rocha, E., Staicu, V.: Quasilinear elliptic system with measure data. Nonlinear Anal. 154, 210–224 (2017)
Leonetti, F., Rocha, E., Staicu, V.: Smallness and cancellation in some elliptic systems with measure data. J. Math. Anal. Appl. 465, 885–902 (2018)
Mingione, G.: The Calderón-Zygmund theory for elliptic problems with measure data. Ann. Sc. Norm. Super. Pisa Cl. Sci. 6, 195–261 (2007)
Mingione, G.: Gradient estimates below the duality exponent. Math. Ann. 346, 571–627 (2010)
Mingione, G.: Nonlinear measure data problems. Milan J. Math. 79, 429–496 (2011)
Mingione, G.: La teoria di Calderon-Zygmund dal caso lineare a quello non lineare. Boll. Unione Mat. Ital. 9, 269–297 (2013)
Oppezzi, P., Rossi, A.M.: Esistenza di soluzioni per problemi unilateri con dato misura o in \(L^1\). Ric. Mat. 45, 491–513 (1996)
Zhang, C., Zhou, S.: Entropy solutions for a non-uniformly parabolic equation. Manuscr. Math. 131, 335–354 (2010)
Zhou, S.: A note on nonlinear elliptic systems involving measures. Electron. J. Differ. Equ. 8, 1–6 (2000)
Acknowledgements
The authors would like to thank the anonymous referee for careful reading of the original version of this paper, and giving valuable comments and suggestions. Ren was partially supported by NSF of Hebei Province under grant no.A2018201285 and the research funding for high-level innovative talents of Hebei University under grant no.8012605. Gao was partially supported by NSF of Hebei Province under grant no. A2019201120.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Gao, H., Huang, M., Deng, H. et al. Global integrability for solutions to quasilinear elliptic systems. manuscripta math. 164, 23–37 (2021). https://doi.org/10.1007/s00229-020-01183-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00229-020-01183-5