Abstract
Branches are not only of vital importance to tree physiology and growth but are also one of the most influential features in wood quality. To improve the availability of data throughout the forest-to-industry production, information on internal quality (e.g. knots) of both felled and standing trees in the forest would be desirable. This study presents models for predicting the internal knot diameter of Douglas-fir logs based on characteristics measured in the field. The data were composed of 87 trees (aged from 32 to 78 years), collected from six trial sites in southwest Germany, and cut into 4–5 m logs on-site. The internal knot diameter was obtained by applying a knot detection algorithm to the CT images of the logs. Applying the Random Forest (RF) technique, two models were developed: (1) MBD: to predict the branch diameter (BD) at different radial positions within the stem, and (2) MBDmax: to predict the maximum internal branch diameter (BDmax). Both models presented a good performance, predicting BD with an RMSE of 4.26 mm (R2 = 0.84) and BDmax with an RMSE of 5.65 mm (R2 = 0.78). In this context, the innovative combination of CT technology and RF modelling technique showed promising potential to be used in future investigations, as it provided a good performance while being flexible in terms of input data structure and also allowing the inclusion of otherwise underexplored databases. This study showed a possibility to predict the internal diameter of branches from field measurements, introducing an advance towards connecting forest and sawmill.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Branches are vital for tree development and as such, constitute an inherent feature in solid timber products, influencing their utilization from a wood technology perspective. Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco), as most coniferous species, typically develops its branches according to its annual longitudinal growth, forming “whorls” (groups of branches growing at the same longitudinal position in the stem). Douglas-fir may develop branches between the whorls, which originate from adventive buds in an irregular longitudinal pattern, and these “internodal branches” are typically smaller in dimension (length and diameter) than “whorl branches”. In the wood products context, knots (the portion of the branch enclosed within a log) represent a disruption of the longitudinally oriented wood matrix of the stem. The area of a log adjacent to knots suffers a significant reduction in its elastomechanical properties due to grain angle deviation in and around knots (Grace et al. 2006) and may also result in aesthetic and processing disadvantages. Therefore, when processing logs to sawn timber or veneer, knots normally have a negative effect on volume (Fahey et al. 1991) and value recovery (Barbour and Parry 2001; Gartner 2005).
From the wood quality and processing point of view, a quantitative assessment of the value-determining characteristics of knots (e.g., position within the log, size, angle, sound/dead status) early in the production chain would be beneficial for both forest growers as sellers and forest product industry as buyers of logs, since logistics, processing decisions and pricing can be based on these important quality criteria. Consequently, current log grading rules try to judge internal knot characteristics based on branch features measured from the outside of the stem. Such branches are obtained after felling in the forest or at the log yard, or even earlier, on the basis of branch features measured on standing trees.
For precise determination of log quality and prediction of timber quality for production, a number of log sorting rules exist which use a limited number of knot measurements, mostly visually assessed on logs in the forest (i.e. felled trees after bucking) or by optical measurements on the log yard of a sawmill (CEN 2008). These established log sorting rules for conifers define log grades according to the diameter of the largest branch visible on the log surface (Anonymous 2015; CEN 2008). In conifers, this typically is a whorl branch. Therefore, standard inventory protocols of tree data acquisition contain measurements of the largest branch within a whorl.
A number of measurement protocols have been developed for recording branch and knot patterns on standing trees during inventories to build models that describe knot distribution (Colin and Houllier 1991; Maguire et al. 1994; Nemec et al. 2012), frequency (Mäkinen and Colin 1999), and longevity/mortality (Hein et al. 2009; Hein and Weiskittel 2010; Kershaw et al. 1990), as well as to explain the factors that drive and/or influence branch and crown development (Hein et al. 2008a, 2008b). External branch diameter models using parameters acquired in the forest as input variables have been built for Douglas-fir over the years. Such models vary in form according to the data available and the intended application/aim of the model. Maguire et al. (1994) predicted the maximum branch diameter in young Douglas-fir trees using a quadratic-quadratic segmented polynomial model from depth into crown, diameter at breast height (DBH), tree height (H), and relative depth into crown (DINC). Weiskittel et al. (2007) used the DBH, H, relative branch height above ground, crown ratio, and crown length (CL) as input variables to a nonlinear multi-level mixed-effects model to predict the maximum branch diameter within the annual shoot. Hein et al. (2008a) fitted linear and nonlinear generalized mix effects models to predict the diameter of the thickest branch per whorl using DBH, H, H/DBH, and the ratio between distance from whorl to stem apex and CL as input variables. However, since such models use external branch diameter measurements as equivalent to internal branch diameters, these approaches have limitations, since it is impossible “to look inside the log before cutting” and therefore the relation between “outside” and “inside” cannot be expressed quantitatively, but remains a more qualitative assessment.
One of the most successful techniques to non-destructively acquire information on the internal structural features of a log is the computed tomography (CT). Studies have been conducted to develop algorithms and models that identify and quantitatively describe a variety of wood features from CT images, for example, the occurrence, morphology, and geometry of knots (Bhandarkar et al. 1999; Johansson et al. 2013; Krähenbühl et al. 2016; Nordmark 2003; Rojas et al. 2006; Roussel et al. 2014; Wei et al. 2008). In recent years, advances in CT research led to the possibility of assessing knot occurrences before the breakdown in sawmills at an industrial pace (Giudiceandrea et al. 2011; Ursella et al. 2018). In this context, CT data has been used to optimize the bucking procedure (Mäkinen et al. 2020), as well as the sawing process in terms of volume (Fredriksson and Broman 2017; Stängle et al. 2015), value (Belley et al. 2019; Fredriksson 2014; Fredriksson et al. 2017; Oja et al. 2010; Rais et al. 2017, Rinnhofer 2003), and aesthetics (Breinig et al. 2014) based on internal knot features. As knots are a result of tree growth, the information acquired through the CT scanning technique is also useful for forest management, giving the possibility to model knots to understand the influence of site conditions and forest management on sawmill’s yield (Fredriksson and Broman 2017; Rais et al. 2020), or potentially to predict knot characteristics in the previous step of the supply chain (ideally from standing trees) in the future. Thus, CT measurements can support efforts to establish a better link between tree growth and timber quality.
As data acquisition in and about forests is time-consuming, onerous, and complex, it frequently results in unbalanced or incomplete datasets, posing challenges to the use of traditional statistical analysis and modelling techniques. Such methodologies are only statistically valid as long as assumptions made a priori about the data structure and distribution are met. Alternatively, machine learning (ML) techniques do not require such pre-assumptions, presenting the potential to be applied to forestry in general, and allowing the use of new as well as archived, underexplored valuable databases.
In recent years, ML models have gained increasing attention, mostly due to their ability to deal with complex, high-dimensional interactions. As one of the most versatile ML algorithmic models, Random Forest (RF) is able to address nonlinear and hierarchical data, allowing the exploration of non-intuitive relationships, ultimately providing highly predictive power (Cutler et al. 2007). Although RF has been reported to present performance reduction due to collinearity (Dormann et al. 2013; Murphy et al. 2010), it has been successfully applied to forestry (Finch et al. 2017; Moore and Lin 2019; Schubert et al. 2020), forest ecology (Cutler et al. 2007; Evans et al. 2011; Evans and Cushman 2009; Mi et al. 2017), and remote sensing studies (Amirruddin et al. 2020; Li et al. 2020; Malek et al. 2019; Moser et al. 2017). Moreover, RF is insensitive to autocorrelation and missing values (De'ath and Fabricius 2000), makes no assumptions about the distribution of input or target variables (Cutler et al. 2007), and is recognized for providing accurate results while dealing with small datasets and a high number of input variables (Biau and Scornet 2016). These characteristics suggest the application of the RF modelling technique to the complex issue in this study.
This study aimed to predict the knot (internal branch) diameter of Douglas-fir trees, based on measurements from outside the tree after felling. To model the target variables, CT scanning and an automated knot detection algorithm were used to acquire the internal branch diameters. Furthermore, due to the unbalanced composition of the data, RF was the modelling technique applied in this study. Two RF models were developed: one to predict the internal knot diameter along the radial direction of the stem, and one to predict the maximum internal knot diameter. In theory, the maximum diameter could be estimated from the first model. However, two models are provided due to the possible applications of each model; the first can be implemented into tree growth models, and the second can be applied to roundwood quality grading. Additionally, after a comprehensive analysis of the RF results, it was possible to select the most important input variables, which can be used in targeted investigations aimed at estimations of branch-based wood quality.
Material and methods
Study sites and data acquisition
Data from 87 Douglas-fir trees from six trial sites in Baden-Württemberg, Germany, were used in this study (Table 1). Data collection and material sampling took place in several earlier projects with slightly different scopes. The material includes trees in different stages of development, with individuals aged between 30 to 80 years. A more detailed description of the data can be found in the literature (Brüchert et al. 2017; Kenk and Thren 1984; Kohnle et al. 2012; Seho and Kohnle 2014).
Field measurements
Trees were felled, measured on-site, and cut into logs of different standard length, starting either from the stump height (sites D, E, and F) or from 1.3 m height (sites A, B, and C), up to the minimum log merchantable diameter of 7 cm. This difference in the input data is present because a disc was sampled at the 1.3 m height at sites A, B, and C. Therefore, in the material from these sites, the first scanned log started at 1.3 m, instead of at the stump height, resulting in a shorter length of the first log.
A detailed field measurement protocol (Brüchert et al. 2017) was applied. It consisted of several tree and whorl characteristics, which were used as input variables (Table 2) in the modelling phase. After the field measurements, the logs were uniquely marked for further identification and transported to the Forest Research Institute of Baden-Württemberg (FVA).
Computed Tomography (CT) data
To mimic operative sawmill conditions, logs were CT scanned in their fresh state, i.e. as soon as possible after they arrived at the log yard. The logs were scanned using the MiCROTEC CT.LOG scanner (Giudiceandrea et al. 2011), a prototype developed for research purposes. The scanner captures the X-ray attenuation of the log, i.e. the difference of emitted and received energy by the scanner, which is directly related to the total density of the log (Freyburger et al. 2009; Lindgren 1991). From the X-ray attenuation of the log, grey-level images can be generated, in which each level of grey represents the log density on a scale with water density as a reference, exposing high (bright) and low (dark) density areas. Each grey-level image represents one slice of 5 mm thickness of the log in the transversal plane (cross-cuts). The image has a voxel size of 1.107 × 1.107 × 5 mm (width × height × depth). When organized by longitudinal position, a group of such images in a row forms a virtual three-dimensional log.
These reconstructed grey-level images are the input of algorithms designed to automatically detect features within the logs. The detection of features, i.e., knots, began with pith detection throughout the log length (Boukadida et al. 2012), which is the core information for subsequent analyses. In a consecutive step, borders were delineated (Baumgartner et al. 2010; Longuetaud et al. 2007), separating regions of distinct density contrasts, i.e., heartwood-sapwood, sapwood-bark, bark-outside. These borders are important because they influence image analysis and interpretation due to the knot detection algorithm used in this study (Johansson et al. 2013). The algorithm has a variety of settings that can be adjusted according to the log species, moisture condition, size, etc. Different configurations of the knot detection algorithm for Douglas-fir were tested by Longo et al. (2019), and the most suitable configuration was the one applied in this study.
The result of the knot detection algorithm is a set of variables that uniquely describe the geometry of each knot. One of them is the knot diameter (ø(r)), which is calculated as a function (Eq. 1) of the radial position (Grönlund et al. 1995). This variable was converted to a linear measure using a mathematical transformation (Eq. 2). Knot diameter was calculated at intervals of 20 mm along the log radius, from pith to bark (Longo et al. 2019).
ø = knot diameter correspondent arc, as given by the knot detection algorithm output (in rad).
RPOS = radial distance, from pith to bark (in mm).
A and B = knot-unique coefficients given as output of the knot detection algorithm.
BD = transformed linear knot diameter (in mm).
The variables acquired through the CT method were BD, BDmax, DWH, and RPOS (Table 2). Both internal diameters (BD and BDmax) are the target variables of this study, while RPOS is considered an input variable since it consists of the radial location of the knot diameter measurement within the stem. The input variable DWH was derived from the CT data based on the CT border detection step (bark-outside border) and not from field measurements.
Modelling approach
This study applied Random Forest Regression (RFR) to generate two models: (1) MBD, a prediction of the internal branch diameter at a given position in the radial direction; and (2) MBDmax, a prediction of the maximum internal branch diameter. The target variables were obtained through image analysis of CT scans, while the input variables were obtained from field measurements, except DWH and RPOS.
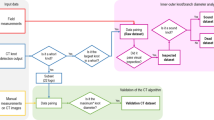
The data were divided into training and testing datasets, in order to build the RFR model and apply it to previously unseen data for model evaluation, respectively. The data (87 trees) were divided into two subsets: 70% composed the training set and 30% composed the testing set. This division was done using a random sampling process at the whorl level for each site separately, resulting in data from all sites in both subsets. The implemented approach is summarized in Fig. 1.
Random Forest Regression (RFR)
Random forest is a powerful algorithm based on Classification and Regression Trees (CARTs) and bagging (Breiman 1996, 2001; Breiman et al. 1984). It builds an ensemble (i.e. a forest) of individual regressors (i.e. decision trees—DT), each accurately covering a given variability within the training data considered (Dietterich 2000). A single DT presents a high susceptibility to overfitting (i.e. DTs growing excessively, performing well on the training data, but poorly on testing sets). In addition, there is bias and high variance between different DTs (Molnar 2019). However, by averaging the predictions of each considered DT in the forest, highly accurate overall predictions can be achieved (Breiman 2001).
DT is a nonparametric hierarchical analysis that uses a random sample (with replacement) of the training data to build a ramified decision path. Approximately one third of the training data sampled for a given DT is randomly left aside to compose the so-called out-of-bag (OOB) data. These data are used to obtain an unbiased estimate of the error of that particular DT.
DT (Fig. 2) starts with a single node (i.e. root), which ramifies based on a random sample of the input variables available in the training data. Each node applies a binary test function to one input variable, which splits the observations and turns the DT more informative at each level until it reaches a leaf node, from which it will not split further, either because there is only one observation left in the node or the pre-defined pruning parameters of the modelling settings (e.g. minimum number of observations in a node) have been reached. Each node contains the mean value of the target variable (BD or BDmax) and the number of observations related to this mean. This process produces one model per DT, predicting the target variable (BD or BDmax) according to the different paths between root and leaf nodes. Considering the decision tree presented in Fig. 2 as an example, the respective model from it would predict a BD of 17 mm when RPOS is lower than 110 mm and DWH is between 179 and 244 mm.
Example of a decision tree generated from the training data (MBD). The depth (number of levels in a tree) was limited to five to improve the visibility of nodes. The numbers inside the boxes (nodes) indicate the knot diameter prediction at that point, and the percentage of the total training dataset that is being considered in that node. At root and internal nodes, a test function regarding one explanatory variable is presented. Left and right options originating from a node always represent yes and no decisions from the test function, respectively
To observe the relationships between variables, the training data was analysed using Spearman’s correlation (due to nonparametric variables present in the data). To select and/or reduce the variables used, Recursive Feature Elimination (Guyon and Elisseeff 2003) with tenfold Cross-Validation and 3 repetitions (RFECV) was applied. RFECV trains a baseline RFR model with all available predictors and computes the mean square error (MSE) on the OOB data for each DT. As the aim of this step was to select the variables that minimize model error, the procedure was repeated permuting the variables, generating an MSE value each time. Ultimately, the RFECV yields the number of selected variables, as well as the variables that provide the optimal scenario concerning model error for the training data. The root of the MSE value was calculated and presented as an error metric (RMSE) for interpretation and comparison purposes. Furthermore, with the stepwise reduction in the number of variables, the RFECV also decreases overall processing times in the subsequent steps.
After the optimal subset of variables was selected in the RFECV analysis, the tuning of hyperparameters (thresholds used to control the machine learning process) was conducted. The hyperparameters ntree (number of DTs to grow), mtry (number of input variables randomly selected to be considered as a splitting parameter at each node), and maxnodes (maximum allowed number of leaf nodes) can be tuned to optimize memory efficiency and computing time, and/or to improve model performance. The latter was exclusively considered for this study. The hyperparameter tuning is performed by iteratively changing and running the algorithm on a range of values for each hyperparameter. Thus, values were tested for ntree (100 to 2000 with steps of 100 trees), mtry (1 to 9 or 8, for MBD and MBDmax respectively, in steps of 1 variable), and maxnodes (100 to 1000 in steps of 100 leaf nodes). The hyperparameter tuning was assessed by applying tenfold cross-validation (CV) with 3 repetitions. Ultimately, the RMSE generated in each fold of the CV is averaged across the folds and repetitions, generating an RMSE per combination of hyperparameter settings (e.g. ntree = 300, mtry = 4, maxnodes = 200 is one combination). The optimal combination of hyperparameters was considered as the one with an RMSE that did not differ in more than 1% from the lowest RMSE value (1% tolerance).
RFR training was done by applying the bootstrap aggregation technique (Breiman 1996) to generate ntree random subsamples (with replacement) of the training data. During the process of growing DTs, a subset of mtry predictor variables was randomly drawn at each splitting node, enabling the determination of the optimal split for each particular subset of variables. This step was conducted recursively, limited by the maxnodes pruning (stopping) criterion. The prediction of an individual DT is the mean of the target variable values of the respective leaf nodes. The overall RFR prediction is computed by averaging the individual predictions of each DT for a given observation.
To quantify each variable’s relative contribution to the predictive models, the Permutation-based Variable Importance (PVI) (Liaw and Wiener 2002) was the metric used. It is one of the most robust and commonly used variable importance (VI) scores for RFR (Molnar 2019). The idea behind the PVI metric is to randomly permute all values of a variable, and the importance score of this variable is defined as the reduction in model predictive performance (mean decrease error, MDE) after the permutation. If a variable is very predictive, then permuting its values will considerably affect the final model performance. Generally, variables selected at or close to the root of a tree are more important than the remaining ones, since splits near the origin of a tree lead to higher information gain.
For model performance, two indices were used to evaluate the predictive strength of the RFR training model: the pseudo coefficient of determination (R2) and the root-mean-squared error (RMSE) of the OOB estimations.
The analysis was carried out exclusively in R (R Core Team 2020), using the additional packages: caret (Kuhn 2019), ggplot2 (Wickham 2016), gridExtra (Auguie 2017), Metrics (Hamner and Frasco 2018), randomForests (Liaw and Wiener 2002), rpart (Therneau and Atkinson 2018), and rpart.plot (Milborrow 2019).
Results and discussion
Optimal number of variables
The analysis started with a set of 13 candidate input variables acquired to predict BD and BDmax. Figure 3 illustrates the strength of correlation between the considered variables. There is a strong correlation, especially concerning age, likely because the dataset consists of trees from three narrow age intervals (Table 1). Furthermore, certain variables have a well-known biological relationship, i.e. DBH and H. However, variables such as WH, WRH, and DINC, which represent different perspectives of the whorl position within the tree, when used simultaneously might clutter the model due to collinearity and might not result in a variance explanation gain. Therefore, the RFECV was applied to avoid bias on the variable selection, as well as to assess the importance of the variables to the RFR model. According to the RFECV results, RFR models with more than nine (MBD) and eight (MBDmax) selected variables do not improve the model performance by more than 1%. Thus, the variables selected within the RFECV analysis for MBD were CBH, CR, DINC, DWH, HD, RDINC, RPOS, WH, WRH; and for MBDmax were CBH, DBH, DINC, DWH, H, HD, SBW, WRH (their relative importance is presented in the section Variable importance). The selection was made to minimize the RMSE in the training dataset from the OOB data throughout the cross-validation runs (Fig. 4).
Spearman correlation matrix of the variables assessed in the training data for MBD (a) and MBDmax (b). Narrow ellipses indicate a higher correlation between variables. The colours indicate the direction and intensity of the correlation according to the scale. Regarding colours, the reader is referred to the digital version of this article
Root-mean-squared error (RMSE) versus the number of predictor variables according to the RFECV analysis. The RMSE values shown are the average over multiple runs. Circles represent values for MBD and squares for MBDmax. The star indicates the number of variables that presents the lowest value of RMSE with 1% of tolerance
Optimal hyperparameters
Based on the selected variables, it was possible to test the RFR model hyperparameters. The fine-tuning of ntree, mtry, and maxnodes in the present study resulted in a total of 18,000 and 21,000 model adjustments for the MBD and MBDmax, respectively. Figure 5 shows the results of the hyperparameter tuning step, in which a minimum value of RMSE in the order of 4.3 mm was achieved for MBD and 6.0 mm for MBDmax. These results were obtained using the combination of ntree = 500, mtry = 2, and maxnodes = 800 for MBD, and ntree = 700, mtry = 2, and maxnodes = 600 for MBDmax (Fig. 5).
Root-mean-squared error (RMSE) curves for MBD and MBDmax with different hyperparameter configurations (hyperparameter tuning step). Dashed elements indicate the hyperparameter configuration with the lowest RMSE value for each model (with 1% tolerance). Regarding colours, the reader is referred to the digital version of this article
Variable importance
With the model’s optimal hyperparameter settings identified, the mean squared error was calculated to provide the importance of each input variable to the model (Fig. 6). The analysis yielded the highest importance of the variables RPOS, DWH, and DINC in decreasing order of importance for the MBD. For MBDmax, the analysis resulted in variables DWH, SBW, followed by DINC in decreasing order of importance.
The assessment of variable importance showed RPOS as the most important variable for MBD. It was expected that such a variable would occupy a high position on the VI ranking, considering that RPOS was the only intra-branch variable in the dataset. Since the internal branch diameter represents the knot diameter expected to be seen in sawn products (Fredriksson et al. 2015; Todoroki et al. 2005; Weiskittel et al. 2006), the RPOS variable is particularly useful in further applications, to predict internal quality (i.e. internal branch diameter) at any radial position within the stem. RPOS was therefore considered to be an input variable, depending on the product settings the user desires (e.g., for a central square block of 120 mm width the user could input RPOS of 60 mm to predict the vertical knot diameter at the surface of the product). The second and third variables in the importance rankings were DWH and DINC, respectively. The tree diameter has been reported as positively correlated to branch size in coastal Douglas-fir (Maguire et al. 1991), Norway spruce (Colin and Houllier 1992), and Scots pine (Mäkinen and Colin 1998).
DWH for this study was derived from the CT scans. In practical applications of this model, this variable could be acquired in the field using traditional direct measurement methods (e.g. with a calliper) on felled trees, indirectly via remote sensing techniques in standing trees (Kankare et al. 2016; Pitkänen et al. 2019; Xie et al. 2020) or estimated through taper functions (Demaerschalk and Kozak 1977; Fonweban et al. 2011; Rustagi and Loveless Jr. 1991) based on DBH and H measurements. The effect of obtaining DWH through another method (field measurements, remote sensing techniques, or taper functions) on the model performance should be investigated in future studies. The variable DINC represents the longitudinal position of the branch within the crown. DWH and DINC cover the variability related to tree growth (i.e., tree vigour, site conditions) and space management in the stand (i.e., tree competition: planting density and thinning regime).
Variable importance analysis for MBDmax showed DWH as the first highlighted variable, followed by SBW and DINC. Knot properties are known to be normally related to the tree diameter growth (Høibø et al. 2002; Vestøl and Høibø 2001), while DINC has been reported as accounting for most of the variation of the BDmax estimation at a given whorl for Douglas-fir (Maguire et al. 1991). The importance of the knot status (SBW) for BDmax, as it shows the prominent position in the importance ranking analysis, can be explained by the different diameter development of sound and dead branches. Although the CT knot detection has limitations (Longo et al. 2019), sound knots have not reached their diameter peak internally yet in comparison to dead knots, which show a clear BDmax within the log.
Model performance
With the optimized combination of hyperparameters, the model was fitted to the training data and the trained model was then applied to the testing data. The resulting model performance is summarized in Table 3. For MBD, a maximum R2 of 0.85 was found in the training step, which translated to an R2 of 0.84 in the test set, whereas for MBDmax, the training yielded a maximum R2 value of 0.77, while the test set presented an R2 value of 0.78. The closer the results of training and testing are, the lower is the degree of overfitting in the model. Figure 7 shows the CT-derived internal branch diameter BD and BDmax against the model prediction. The model residual plots indicate no systematic pattern of deviation.
The first model (MBD) was adjusted aiming to provide information on internal branch diameter at different radial positions inside the stem, supporting future investigations on the internal quality of Douglas-fir related to sawn timber products. Since the branch diameter measurements (BD and BDmax) were obtained vertically (parallel to the log axis) from CT image analysis, a direct approximation of the knot diameter on boards can be assumed. Therefore, such a model would likely provide valuable data to, for example, sawn timber simulation models (Poschenrieder et al. 2016). The second model (MBDmax) was developed aiming at a more revealing roundwood quality assessment, which focuses on the maximum internal knot diameter instead of the maximum branch diameter measured from outside at the stem surface (e.g. as log sorting rules such as EN 1927–3 (CEN 2008) or RVR (Anonymous 2015) stipulate), which would show a closer relation to the maximum knot diameter obtained when the log is processed in the wood industry.
Results showed a good performance of MBD in the testing set (R2 = 0.84, RMSE = 4.3 mm, N = 1753 branch diameters). Applying a two-stage process involving first the estimation of individual knot parameters (nonlinear mixed-effects model) and then modelling internal BD as a function of tree and branch variables (gamma regression with a log-link and linear mixed-effects model with random tree effect), Duchateau et al. (2013) reported that 75% of the residuals were less than 1.4 mm for black spruce (Picea mariana [Mill.] SBP) and 95% of the residuals were less than 2.4 mm for jack pine (Pinus banksiana Lamb.). The authors obtained these results using a medical CT scanner to acquire BD and the following input variables: external branch diameter, knot inclination at the bark, total knot length, relative position along the stem, H, and HD. However, the use of internal measurements as input variables, the higher resolution of the CT scanner used in their study, the different species, and overall purpose of the model impede a more direct comparison to the present study.
Considering the different data acquisition used in this study (CT scanning and field measurements), the MBDmax performed well (R2 = 0.78, RMSE = 5.6 mm, N = 728 branches) in the testing data. The results achieved in this study are close to the range for BDmax models found in the literature. Kershaw et al. (2009), when modelling external BDmax for black spruce, observed the best results (adjusted R2 = 0.73, RMSE = 2.45 mm) for a nonlinear mixed-effects model from a total of six model variants and three nonlinear fitting techniques (least-squares, generalized least-squares, and mixed-effects), using as input variables DINC and the depth of the branch below crown base (= height to crown base – WH). Weiskittel et al. (2007) found an R2 = 0.80 (residual standard error = 4.45 mm) in the estimation of external BDmax of coastal Douglas-fir in the United States with CL and branch relative height as input variables. Hein et al. (2008a) modelled the external BDmax from widely spaced Douglas-fir trees in Germany using a nonlinear generalized linear mixed model that explained 85.9% of the total variance (92.7% including random effects) by using DBH, H, and RDINC as input variables. These model statistics are not directly comparable to the RFR model strength achieved in this study. Hein et al.’s model considered exclusively live branches and used a BDmax obtained on the log surface in the field as a target variable. In contrast, the present study included both live and dead branches, BDmax consisted of an internal measurement, and a different branch diameter measurement technique was applied (CT scanning). In particular, the combination of dead knots and the CT method add variance to MBDmax, due to detection accuracy (Longo et al. 2019).
The inclusion of more branch-related variables, for example, branch length, as well as variables at a higher level, for example, site index, might improve the overall performance of the models. The use of mainly tree-level field measurements as input variables would support the realization of a quality-related prediction early in the wood production chain. Recently conducted research (Brüchert et al. 2019; Grace et al. 2015; Pyörälä et al. 2018; Saladin 2014) indicate a shift towards remote data acquisition through aerial or terrestrial-based methods, i.e. aerial images, LiDAR, close-range photogrammetry, among others used for wood quality assessment and forecast.
In principle, the models fitted in this study depend essentially on the accuracy of the CT knot diameter outputs. These may not always be precise, as reported by Johansson et al. (2013) for Norway spruce (Picea abies [L.] Karst.) and Scots pine (Pinus sylvestris L.), by Fredriksson et al. (2017) for jack pine and white spruce (Picea glauca [Moench] Voss), and by Longo et al. (2019) for Douglas-fir. Therefore, there are opportunities for future improvements in the presented models, as more advanced CT image resolution might provide even higher accuracy, and/or the applied algorithm may undergo modifications to enhance the knot boundary detection, improving the knot size extraction.
RF models are capable of drawing predictions within the variability pool of the information provided to the model in the training phase (Breiman 2001). The present study focused on building the model and presenting a first model performance assessment based on the data randomly set aside during database partitioning.
An independent dataset from areas of similar conditions could be used to provide knot diameter predictions. As further data is made available, the model can then be updated to broaden its variability coverage and generalization capabilities.
Conclusion
This is the first study to use CT scanning to obtain the internal knot diameter of Douglas-fir logs, and subsequently, predict the internal knot diameter (both at a given radial position and the maximum internal value) from external tree characteristics acquired in the forest.
Data analysis revealed that RPOS, DWH, and DINC were the most important predictors for branch diameter in general, and DWH, SBW, and DINC were the variables of higher importance for predicting BDmax.
Although the evaluation of the model technique was not the focus of this study, it was noticed that RFR seems promising for this application since it does not require the data to be of a particular distribution or structure and provides a robust performance. The introduction of this advanced statistical method opens new paths in wood technology since in many investigations, data might have a similar (unbalanced) structure to the dataset in this study.
In general, both models showed a good overall performance, especially the BDmax model. However, the quality of these models relies on the accuracy of the applied CT knot detection algorithm. Thus, improvements in the algorithm’s performance might yield an enhanced prediction accuracy, which could be used in further applications in wood processing.
In terms of application, these models represent an advance regarding the connection between forest operations, management, and roundwood (and eventually sawn timber) quality assessment. Ideally, models presented in this study would evolve to receive input field data acquired remotely, allowing the construction of a larger and comprehensive database for inner log quality. Future studies should focus on the link between methodologies that facilitate field data acquisition and non-destructive techniques capable of capturing the internal branch structure. Moreover, further investigations could apply the models presented in this study to independent data (1) from similar conditions to obtain knot diameter predictions; and (2) outside the variation spectrum used in this study to expand the models in terms of variability coverage and application.
References
Amirruddin AD, Muharam FM, Ismail MH, Ismail MF, Tan NP, Karam DS (2020) Hyperspectral remote sensing for assessment of chlorophyll sufficiency levels in mature oil palm (Elaeis guineensis) based on frond numbers: analysis of decision tree and random forest. Comput Electron Agric 169:105221
Andreu J-P, Rinnhofer A (2003) Modeling of internal defects in logs for value optimization based on industrial CT scanning. In Proceedings of the Fifth Conference on Image Processing and Scanning of Wood. A. Rinnhofer (ed.), March 23–26 2003, Bad Waltersdorf, Austria. pp. 141–150
Anonymous (2015) Rahmenvereinbarung für den Rohholzhandel in Deutschland (RVR) des Deutschen Forstwirtschaftsrates e.V. und des Deutschen Holzwirtschaftsrates e.V. [Framework Agreement for the Raw Timber Trade in Germany (RVR) of the German Forestry Council and the German Timber Industry Council] 2nd updated edition
Auguie B (2017) gridExtra: Miscellaneous Functions for “Grid” Graphics. R package version 2.3. https://CRAN.R-project.org/package=gridExtra. Accessed 15 September 2020
Barbour RJ, Parry DL (2001) Log and lumber grades as indicators of wood quality in 20- to 100-year-old Douglas-fir trees from thinned and unthinned stands. Gen. Tech. Rep. General Technical Report (GTR). PNW-GTR-510. Portland, OR: U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station. p. 22
Baumgartner R, Brüchert F, Sauter UH (2010) Knots in CT scans of pine logs. In The Future of Quality Control for Wood and Wood Products, The Final Conference of COST Action E53, Edinburgh, United Kingdom, 4–7 May 2010. Dan Ridley-Ellis and John Moore (eds)
Belley D, Duchesne I, Vallerand S, Barrette J, Beaudoin M (2019) Computed tomography (CT) scanning of internal log attributes prior to sawing increases lumber value in white spruce (Picea glauca) and jack pine (Pinus banksiana). Can J for Res 49:1516–1524
Bhandarkar SM, Faust TD, Tang M (1999) CATALOG. a system for detection and rendering of internal log defects using computer tomography. Mach vis Appl 11:171–190
Biau G, Scornet E (2016) A Random Forest Guided Tour. Test 25:197–227
Boukadida H, Longuetau F, Colin F, Freyburger C, Constant T, Leban JM, Mothe F (2012) PithExtract. A robust algorithm for pith detection in computer tomography images of wood—Application to 125 logs from 17 tree species. Comput Electron Agric 85:90–98
Breiman L (1996) Bagging predictors. Mach Learn 24:123–140
Breiman L (2001) Random forests. Mach Learn 45:5–32
Breiman L, Friedman JH, Stone CJ, Olshen RA (1984) Classification and regression trees. Chapman & Hall/CRC, Boca Raton - FL.
Breinig L, Leonhart R, Broman O, Manuel A, Brüchert F, Becker G (2014) Classification of wood surfaces according to visual appearance by multivariate analysis of wood feature data. J Wood Sci 61:89–112
Brüchert F, Baumgartner R, Montoya DH, Sauter UH (2017) FastForests: Untersuchungen zur Holzqualität der Douglasie unter Berücksichtigung der Wuchsgeschwindigkeit [Fast Forests: Impacts of faster growing forests on raw material properties with consideration of the potential effects of a changing climate on species choice.] Final report. p. 114
Brüchert F, Adler P, Ganz S, Stängle SM, Yue C (2019) Weiterentwicklung statistischer Holzaufkommensprognoseverfahren zur Differenzierung von Rohholzsorten und Produktqualität (Pro-Qual-Tools). [Further development of statistical wood supply forecasting methods for the differentiation of raw wood species and product quality.] Final report. 128p. https://www.fnr.de/index.php?id=11150&fkz=22023114 Accessed 20 June 2020
CEN (2008) CEN 1927–3. 2008–06: Qualitative classification of softwood round timber - Part 3: Larches and Douglas fir. Deutsches Institut für Normung, Berlin
Colin F, Houllier F (1991) Branchiness of Norway spruce in north-eastern France. Modelling vertical trends in maximum nodal branch size. Ann Sci for 48:679–693
Colin F, Houllier F (1992) Branchiness of Norway spruce in northeastern France: predicting the main crown characteristics from usual tree measurements. Ann Sci for 49:511–538
Cutler DR, Edwards TC, Beard KH, Cutler A, Hess KT, Gibson J, Lawler JJ (2007) Random forests for classification in ecology. Ecology 88:2783–2792
De`ath G, Fabricius KE (2000) Classification and regression trees: a powerful yet simple technique for ecological data analysis. ANALYSIS. Ecology 81:3178–3192
Demaerschalk JP, Kozak A (1977) The whole-bole system: a conditioned dual-equation system for precise prediction of tree profiles. Can J for Res 7:488–497
Dietterich TG (2000) Ensemble Methods in Machine Learning. In Multiple classifier systems: First international workshop, MCS 2000/Josef Kittler, Fabio Roli (eds.). J. Kittler and F. Roli (eds). Springer, pp. 1–15
Dormann CF, Elith J, Bacher S et al (2013) Collinearity: a review of methods to deal with it and a simulation study evaluating their performance. Ecography 36:27–46
Duchateau E, Longuetaud F, Mothe F, Ung C, Auty D, Achim A (2013) Modelling knot morphology as a function of external tree and branch attributes. Can J for Res 43:266–277
Evans JS, Cushman SA (2009) Gradient modeling of conifer species using random forests. Landscape Ecol 24:673–683
Evans JS, Murphy MA, Holden ZA, Cushman SA (2011) Modeling Species Distribution and Change Using Random Forest. In Predictive species and habitat modeling in landscape ecology: Concepts and applications/C. Ashton Drew, Yolanda F. Wiersma, Falk Huettmann, editors. C.A. Drew, Y.F. Wiersma and F. Huettmann (eds). Springer, pp. 139–159
Fahey TD, Cahill JM, Snellgrove TA, Heath LS (1991) Lumber and veneer recovery from intensively managed young-growth Douglas-fir. PNW-RP-437. Portland, OR: U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station. p. 25
Finch K, Espinoza E, Jones FA, Cronn R (2017) Source identification of western oregon douglas-fir wood cores using mass spectrometry and random forest classification. Appl Plant Sci 5:12p
Fonweban J, Gardiner B, Macdonald E, Auty D (2011) Taper functions for Scots pine (Pinus sylvestris L.) and Sitka spruce (Picea sitchensis (Bong.) Carr.) in Northern Britain. Forestry 84:49–60
Fredriksson M (2014) Log sawing position optimization using computed tomography scanning. Wood Mat Sci Eng 9:110–119
Fredriksson M, Broman O (2017) Factors affecting volume yield in a forestry-wood value chain—a simulation study based on CT scanning. Pro Ligno 13:540–548
Fredriksson M, Berglund A, Broman O (2015) Validating a crosscutting simulation program based on computed tomography scanning of logs. Eur J Wood Prod 73:143–150
Fredriksson M, Cool J, Duchesne I, Belley D (2017) Knot detection in computed tomography images of partially dried jack pine (Pinus banksiana) and white spruce (Picea glauca) logs from a Nelder type plantation. Can J for Res 47:910–915
Freyburger C, Longuetaud F, Mothe F, Constant T, Leban J-M (2009) Measuring wood density by means of X-ray computer tomography. Ann for Sci 66:804
Gartner BL (2005) Assessing wood characteristics and wood quality in intensively managed plantations. J Forest 103:75–77
Giudiceandrea F, Ursella E, Vicario E (2011) A high speed CT-scanner for the sawmill industry. In: Proceedings 17th International Non-destructive Testing and Evaluation of Wood Symposium, Sopron, Hungary, September 14–16 2011. University of West Hungary
Grace JC, Pont D, Sherman L, Woo G, Aitchison D (2006) Variability in stem wood properties due to branches. NZ J Forest Sci 36(2/3):313–324
Grace JC, Brownlie RK, Kennedy SG (2015) The influence of initial and post-thinning stand density on Douglas-fir branch diameter at two sites in New Zealand. NZ J Forest Sci 45:14
Grönlund A, Björklund L, Grundberg S, Berggren G (1995) Manual för Furustambank. [Manual of the Pine Stem Bank.] Luleå University of Technology. p. 25 http://ltu.diva-portal.org/smash/record.jsf?pid=diva2%3A996216&dswid=-262 Accessed 11 March 2020
Guyon I, Elisseeff A (2003) An introduction of variable and feature selection. J Mach Learn Res 3:1157–1182
Hamner B, Frasco M (2018) Metrics: Evaluation Metrics for Machine Learning. R package version 0.1.4. https://CRAN.R-project.org/package=Metrics. Accessed 15 September 2020
Hein S, Weiskittel AR (2010) Cutpoint analysis for models with binary outcomes: a case study on branch mortality. Eur J Forest Res 129:585–590
Hein S, Weiskittel AR, Kohnle U (2008a) Branch characteristics of widely spaced Douglas-fir in south-western Germany. Comparisons of modelling approaches and geographic regions. Ecol Manage 256:1064–1079
Hein S, Weiskittel AR, Kohnle U (2008b) Effect of wide spacing on tree growth, branch and sapwood properties of young Douglas-fir [Pseudotsuga menziesii (Mirb.) Franco] in south-western Germany. Eur J Forest Res 127:481–493
Hein S, Weiskittel AR, Kohnle U (2009) Models on branch characteristics of wide-spaced Douglas-fir. R.M. D.P. Dykstra (ed). U.S. Dept. of Agriculture, Forest Service, Pacific Northwest Research Station
Høibø O, Turnblom E, Briggs D (2002) Vertical profiles of knot characteristics in young coastal U.S. Doulglas-fir plantations. In: IUFRO WP S5.01.04 Fourth Workshop, Connection between Forest Resources and Wood Quality: Modelling Approaches and Simulation Software. G. Nepveu (ed). Harrison Hot Springs, British Columbia, Canada. September 8–15, 2002. 274–281
Johansson E, Johansson D, Skog J, Fredriksson M (2013) Automated knot detection for high speed computed tomography on Pinus sylvestris L. and Picea abies (L.) Karst. using ellipse fitting in concentric surfaces. Comput Electron Agric 96:238–245
Kankare V, Puttonen E, Holopainen M, Hyyppä J (2016) The effect of TLS point cloud sampling on tree detection and diameter measurement accuracy. Remote Sens Letts 7:495–502
Kenk G, Thren M (1984) Ergebnisse verschiedener Douglasienprovenienzversuche in Baden-Württemberg. Teil I. Der Internationale Douglasien-Provenienzversuch 1958. [Results of differents Douglas-fir provenances trials in Baden-Württemberg. Part I: the International Douglas-fir provenance trial 1958.]. Allgemeine Forst-Und Jagdzeitung 155:165–184
Kershaw JA, Maguire DA, Hann DW (1990) Longevity and duration of radial growth in Douglas-fir branches. Can J Res 20:1690–1695
Kershaw JA, Benjamin JG, Weiskittel AR (2009) Approaches for modeling vertical distribution of maximum knot size in black spruce. A comparison of fixed- and mixed-effects nonlinear models. Forest Sci 55:230–237
Kohnle U, Hein S, Sorensen FC, Weiskittel AR (2012) Effects of seed source origin on bark thickness of Douglas-fir (Pseudotsuga menziesii) growing in southwestern Germany. Can J Res 42:382–399
Krähenbühl A, Roussel J-R, Kerautret B, Debled-Rennesson I, Mothe F, Longuetaud F (2016) Robust Knot Segmentation by Knot Pith Tracking in 3D Tangential Images. In Computer Vision and Graphics: International Conference, ICCVG 2016, Warsaw, Poland, September 19–21, 2016, Proceedings. L.J. Chmielewski, A. Datta, R. Kozera and K. Wojciechowski (eds). Springer International Publishing. 581–593
Kuhn M (2019) Contributions from Jed Wing and Steve Weston and Andre Williams and Chris Keefer and Allan Engelhardt and Tony Cooper and Zachary Mayer and Brenton Kenkel and the R Core Team and Michael Benesty and Reynald Lescarbeau and Andrew Ziem and Luca Scrucca and Yuan Tang and Can Candan and Tyler Hunt. caret: Classification and Regression Training. R package version 6.0–84. https://CRAN.R-project.org/package=caret Accessed 15 September 2020
Li M, Zhang Y, Wallace J, Campbell E (2020) Estimating annual runoff in response to forest change: a statistical method based on random forest. J Hydrol 589:125168
Liaw A, Wiener M (2002) Classification and Regression by randomForest. R News 2, 18–22. https://cran.r-project.org/doc/Rnews/Rnews_2002-3.pdf
Lindgren LO (1991) Medical CAT-scanning. X-ray absorption coefficients, CT-numbers and their relation to wood density. Wood Sci Technol 25:341–349
Longo BL, Brüchert F, Becker G, Sauter UH (2019) Validation of a CT knot detection algorithm on fresh Douglas-fir (Pseudotsuga menziesii (Mirb) Franco) logs. Annals Forest Sci 76:28
Longuetaud F, Mothe F, Leban J-M (2007) Automatic detection of the heartwood/sapwood boundary within Norway spruce (Picea abies (L.) Karst.) logs by means of CT images. Comput Electron Agric 58:100–111
Maguire DA, Kershaw JA Jr, Hann DW (1991) Predicting the effects of silvicultural regime on branch size and crown wood core in douglas-fir. Forest Sci 37:1409–1428
Maguire DA, Moeur M, Bennett WS (1994) Models for describing basal diameter and vertical distribution of primary branches in young Douglas-fir. For Ecol Manage 63:23–55
Mäkinen H, Colin F (1998) Predicting branch angle and branch diameter of Scots pine from usual tree measurements and stand structural information. Can J for Res 28:1686–1696
Mäkinen H, Colin F (1999) Predicting the number, death, and self-pruning of branches in Scots pine. Can J Res 29:1225–1236
Mäkinen H, Korpunen H, Raatevaara A, Heikkinen J, Alatalo J, Uusitalo J (2020) Predicting knottiness of Scots pine stems for quality bucking. Eur J Wood Prod 78:143–150
Malek S, Miglietta F, Gobakken T, Næsset E, Gianelle D, Dalponte M (2019) Prediction of stem diameter and biomass at individual tree crown level with advanced machine learning techniques. iForest 12:323–329
Mi C, Huettmann F, Guo Y, Han X, Wen L (2017) Why choose random forest to predict rare species distribution with few samples in large undersampled areas? Three Asian crane species models provide supporting evidence. PeerJ 5:e2849
Milborrow S (2019) rpart.plot: Plot ‘rpart’ models: An Enhanced Version of ‘plot.rpart’. R package version 3.0.8. https://CRAN.R-project.org/package=rpart.plot Accessed 15 September 2020
Molnar C (2019) Interpretable machine learning.: A Guide for Making Black Box Models Explainable. (n.p.) p. 318
Moore J, Lin Y (2019) Determining the extent and drivers of attrition losses from wind using long-term datasets and machine learning techniques. Forestry Int J Forest Res 92:425–435
Moser P, Vibrans AC, McRoberts RE et al (2017) Methods for variable selection in LiDAR-assisted forest inventories. Forestry Int J Forest Res 90:112–124
Murphy MA, Evans JS, Storfer A (2010) Quantifying Bufo boreas connectivity in Yellowstone National Park with landscape genetics. Ecology 91:252–261
Nemec AFL, Parish R, Goudie JW (2012) Modelling number, vertical distribution, and size of live branches on coniferous tree species in British Columbia. Can J for Res 42:1072–1090
Nordmark U (2003) Models of knots and log geometry of young Pinus sylvestris sawlogs extracted from computed tomographic images. Scand J for Res 18:168–175
Oja J, Skog J, Edlund J, Björklund L (2010) Deciding log grade for payment based on X-ray scanning of logs. In: The Future of Quality Control for Wood & Wood Products, The Final Conference of COST Action E53, Edinburgh, May 4–7 2010, Dan Ridley-Ellis and John Moore (eds)
Pitkänen TP, Raumonen P, Kangas A (2019) Measuring stem diameters with TLS in boreal forests by complementary fitting procedure. ISPRS J Photogramm Remote Sens 147:294–306
Poschenrieder W, Rais A, van de Kuilen J-W G, Pretzsch H (2016) Modelling sawn timber volume and strength development at the individual tree level—essential model features by the example of Douglas fir. Silva Fennica 50
Pyörälä J, Kankare V, Vastaranta M et al (2018) Comparison of terrestrial laser scanning and X-ray scanning in measuring Scots pine (Pinus sylvestris L.) branch structure. Scand J Res 33:291–298
R Core Team (2020) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
Rais A, Poschenrieder W, van de Kuilen J-WG, Pretzsch H (2020) Impact of spacing and pruning on quantity, quality and economics of Douglas-fir sawn timber: scenario and sensitivity analysis. Eur J Forest Res 139:747–758
Rais A, Ursella E, Vicario E, Giudiceandrea F (2017) The use of the first industrial X-ray CT scanner increases the lumber recovery value. case study on visually strength-graded Douglas-fir timber. Annals Forest Sci 74:28. 1–9.
Rojas G, Condal A, Beauregard R, Verret D, Hernández RE (2006) Identification of internal defect of sugar maple logs from CT images using supervised classification methods. Holz Roh-Werkst 64:295–303
Roussel JR, Mothe F, Krähenbühl A, Kerautret B, Debled-Rennesson I, Longuetaud F (2014) Automatic knot segmentation in CT images of wet softwood logs using a tangential approach. Comput Electron Agric 104:46–56
Rustagi KP, Loveless RS Jr (1991) Compatible variable-form volume and stem-profile equations for Douglas-fir. Can J for Res 21:143–151
Saladin D (2014) Bestimmung des Astkerndurchmessers an Fichte (Picea abies) aus TLS-Daten. [Determination of the branch core diameter on spruce (Picea abies) from TLS data.] Dissertation, University of Freiburg
Schubert M, Luković M, Christen H (2020) Prediction of mechanical properties of wood fiber insulation boards as a function of machine and process parameters by random forest. Wood Sci Technol 54:703–713
Šeho M, Kohnle U (2014) Der Internationale Douglasien-Provenienzversuch 1958: Unterschiede in der Ausprägung von Ast-und Stammmerkmalen auf den südwestdeutschen Versuchsflächen. [The International Douglas-fir Provenance Trial 1958: Differences in the expression of branch and stem characteristics on the Southwest German trial plots] Allgemeine Forst-und Jagdzeitung 185, 27–42
Stängle SM, Brüchert F, Heikkila A, Usenius T, Usenius A, Sauter UH (2015) Potentially increased sawmill yield from hardwoods using X-ray computed tomography for knot detection. Ann Sci 72:57–65
Therneau T, Atkinson B (2018) rpart: Recursive Partitioning and Regression Trees. R package version 4.1–13. https://CRAN.R-project.org/package=rpart. Accessed 15 September 2020
Todoroki CL, Monserud RA, Parry DL (2005) Predicting internal lumber grade from log surface knots: actual and simulated results. Prod J 55:38–47
Ursella E, Giudiceandrea F, Boschetti M (2018) A Fast and Continuous CT scanner for the optimization of logs in a sawmill. 8th Conference on Industrial Computed Tomography Wells, Austria
Vestøl GI, Høibø OA (2001) Prediction of knot diameter in Picea abies (L.) Karst. Eur J Wood Prod 59:129–136
Wei Q, Leblon B, Chui Y, Zhang SY (2008) Identification of selected log characteristics from computed tomography images of sugar maple logs using maximum likelihood classifier and textural analysis. Holzforschung 62(4):441–447
Weiskittel AR, Maguire DA, Monserud RA, Rose R, Turnblom E (2006) Intensive management influence on Douglas fir stem form, branch characteristics, and simulated product recovery. NZ J Forest Sci 36:293–312
Weiskittel AR, Maguire DA, Monserud RA (2007) Modeling crown structural responses to competing vegetation control, thinning, fertilization, and Swiss needle cast in coastal Douglas-fir of the Pacific Northwest, USA. Ecol Manage 245:96–109
Wickham H (2016) ggplot2: Elegant graphics for data analysis, 2nd edn. Springer, Switzerland, p 260
Xie Y, Zhang J, Chen X, Pang S, Zeng H, Shen Z (2020) Accuracy assessment and error analysis for diameter at breast height measurement of trees obtained using a novel backpack LiDAR system. Ecosyst 7(1):1–11
Acknowledgements
The authors thank Fridolin Sauter, Rafael Baumgartner, Diana Hoyos Montoya, Dr. Stefan M. Stängle, David Umhauer, and Alisa Goedecke for their assistance on field data collection, Jan Hendrik Czopp and Eike Jentner for their assistance on CT manual data acquisition, and João Paulo Pereira for crucial optimization of the CT data outputs.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was supported by the Brazilian Ministry of Education (represented by CAPES and CNPq agencies) and the German Academic Exchange Service (DAAD) through the CAPES/CNPq/DAAD Science without Borders framework [Grant number: 102014, program number 6492, to Longo, B.L.]; and by the Agency for Renewable Resources e.V. (FNR) under the German Federal Ministry of Food and Agriculture [Grant numbers: FKZ22005714, FKZ22037211, FKZ22023114].
Author information
Authors and Affiliations
Contributions
Bruna L. Longo and Franka Brüchert contributed to the study’s conception and design. Material preparation, data collection and analysis were performed by Bruna L. Longo. Franka Brüchert, Gero Becker and Udo H. Sauter supervised the work. The first draft of the manuscript was written by Bruna L. Longo and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
None declared.
Availability of data and material
The datasets analysed in this study are available from the corresponding author on reasonable request.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Longo, B.L., Brüchert, F., Becker, G. et al. Predicting Douglas-fir knot size in the stand: a random forest model based on CT and field measurements. Wood Sci Technol 56, 531–552 (2022). https://doi.org/10.1007/s00226-021-01332-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00226-021-01332-3