Skip to main content

Advertisement

SpringerLink
Log in

A relevant and robust vacuum-drying model applied to hardwoods

  • Original
  • Published:
Wood Science and Technology Aims and scope Submit manuscript

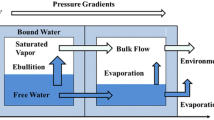
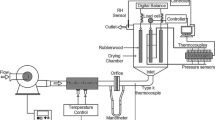
Abstract

A robust mathematical model was developed to simulate the heat and mass transfer process that evolves during vacuum-drying of four commercially important Australian native hardwood species. The hardwood species investigated were spotted gum (Corymbia citriodora), blackbutt (Eucalyptus pilularis), jarrah (Eucalyptus marginata), and messmate (Eucalyptus obliqua). These species provide a good test for the model based on their extreme diversity between wood properties and drying characteristics. The model uses boundary condition data from a series of vacuum-drying trials, which were also used to validate predictions. By using measured diffusion coefficient values to calibrate empirical formula, the accuracy of the model was greatly improved. Results of a sensitivity analysis showed that the model outputs provide excellent agreement with experimental observation despite the large range of species behaviour and variation in wood properties. This study confirms that the drying rate is significantly improved as a direct result of the enhanced convective and diffusive transfer along the board thickness. Contrary to softwood, it appears that longitudinal migration provides only a secondary effect. Not only is the model able to predict the heat and mass transfer behaviour of a range of hardwood species, it is also flexible enough to predict the behaviour for both conventional and vacuum-drying scenarios. The outcomes of this work provide the hardwood industry with a well-calibrated predictive drying tool that can be used to optimise drying schedules.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Abbreviations

c p :

Specific heat (J kg−1 K−1)

c :

Molar concentration (mol m−3)

\(\overline{{{\overline{\mathbf{D}}}}}\) :

Diffusivity tensor (m2 s−1)

FSP:

Fibre saturation point

g :

Gravitational acceleration (m s−2)

h :

Specific enthalpy (J kg−1)

h :

Heat transfer coefficient (W m−2 K−1)

J :

Flux expression

K :

Intrinsic permeability (m2)

\(\overline{{{\overline{\mathbf{K}}}}}\) :

Absolute permeability tensor (m2)

\(\overline{{{\overline{\mathbf{k}}}}}\) :

Relative permeability tensor

k :

Boltzmann’s constant

k a :

Air permeability (m2)

k m :

Mass transfer coefficient (m s−1)

k r :

Relative permeability

L :

Characteristic length (m)

M :

Molecular weight (kg mol−1)

MC:

Moisture content

ΔP :

Pressure difference (Pa)

\(\bar{P}\) :

Average pressure (Pa)

P :

Pressure (Pa)

q:

External heat transfer coefficient (W m−2 °C−1)

R :

Gas constant (J mol−1 K−1)

S :

Volume saturation

t :

Time (s)

T :

Temperature (K)

v :

Mass velocity vector (m s−1)

ν:

Poisson’s ratio

V g :

Green volume (m3)

x :

Molar fraction (mol/mol)

X :

Moisture content (dry basis) (kg kg−1)

ε :

Volume fraction

λ:

Thermal conductivity (W m−1 K−1)

ρ :

Intrinsic averaged density (kg m−2)

ρ 0 :

Wood density (kg m−2)

σ:

Surface tension (N m−1)

σ(T):

Surface tension at temperature T (N m−1)

μ:

Dynamic viscosity of air (Pa s)

φ :

Phase potential

ϕ :

Porosity (m3 m−3)

χ :

Depth scalar (m)

ω:

Mass fraction

a :

Air

b :

Bound

c :

Capillary

e :

Enthalpy

eff:

Effective property

fsp:

Fibre saturation point

g :

Gas phase

l :

Liquid

s :

Solid phase

v :

Vapour phase

ν∞ :

Vapour phase at boundary

w :

Liquid phase

∞:

Value outside the boundary layer in the free stream

References

  • Carr E, Turner I, Perré P (2011) A new control-volume finite-element scheme for heterogeneous porous media: application to the drying of softwood chemical. Eng Technol 34:1143–1150

    Article  CAS  Google Scholar 

  • Carr EJ, Turner IW, Perre P (2013a) A dual-scale modeling approach for drying hygroscopic porous media. Multiscale Model Simul 11:362–384. doi:10.1137/120873005

    Article  Google Scholar 

  • Carr EJ, Turner IW, Perre P (2013b) A variable-stepsize Jacobian-free exponential integrator for simulating transport in heterogeneous porous media: application to wood drying. J Comput Phys 233:66–82. doi:10.1016/j.jcp.2012.07.024

    Article  Google Scholar 

  • Hamby DM (1994) A review of techniques for parameter sensitivity analysis of environmental models. Environ Monit Assess 32:135–154

    Article  CAS  PubMed  Google Scholar 

  • Nolan G, Innes TC, Redman AL, McGavin R (2003) Australian hardwood drying best practice manual. Forest and Wood Products Research and Development Corporation, www.fwpa.com.au

  • O’Neill RV, Gardner RH, Mankin JB (1980) Analysis of parameter error in a nonlinear model. Ecol Model 8:297–311

    Article  Google Scholar 

  • Pang S (2007) Mathematical modeling of kiln drying of softwood timber: model development, validation and practical application. Dry Technol 25:421–431. doi:10.1080/07373930601183751

    Article  CAS  Google Scholar 

  • Perré P (2007) Fundamentals of wood drying. A.R.BO.LOR, Nancy

    Google Scholar 

  • Perré P (2010) Multiscale modeling of drying as a powerful extension of the macroscopic approach: application to solid wood and biomass processing. Dry Technol 28:944–959. doi:10.1080/07373937.2010.497079

    Article  Google Scholar 

  • Perre P, Moyne C (1991) Processes related to drying: part II use of the same model to solve transfers both in saturated and unsaturated porous media. Dry Technol 9:1153–1179. doi:10.1080/07373939108916747

    Article  Google Scholar 

  • Perré P, Turner IW (1999a) A 3-D version of TransPore: a comprehensive heat and mass transfer computational model for simulating the drying of porous media. Int J Heat Mass Transf 42:4501–4521. doi:10.1016/s0017-9310(99)00098-8

    Article  Google Scholar 

  • Perré P, Turner IW (1999b) Transpore: a generic heat and mass transfer computational model for understanding and visualising the drying of porous media. Dry Technol 17:1273–1289. doi:10.1080/07373939908917614

    Article  Google Scholar 

  • Perré P, Turner JW (2008) A mesoscopic drying model applied to the growth rings of softwood: mesh generation and simulation results. Maderas, Ciencia y technologia 10:251–274. doi:10.4067/s0718-221x2008000300008

    Google Scholar 

  • Perré P, Turner I, Remond R (2007) Chapter 1—comprehensive drying models based on volume-averaging: background, application and perspective. In: Tsotsas E, Mujumdar AS (eds) modern drying technology: volume 1: computational tools at different scales

  • Redman AL (2011) Evaluation of super-heated steam vacuum drying viability and development of a predictive drying model for four Australian hardwood species. Report for Forest and Wood Products Australia, http://www.fwpa.com.au

  • Redman AL, Bailleres H, Perré P (2011) Characterization of viscoelastic, shrinkage and transverse anatomy properties of four Australian hardwood species. Wood Mat Sci Eng 6:95–104. doi:10.1080/17480272.2010.535014

    Article  Google Scholar 

  • Redman AL, Bailleres H, Turner I, Perré P (2012) Mass transfer properties (permeability and mass diffusivity) of four Australian hardwood species. BioResources 7:3410–3424

    Google Scholar 

  • Redman AL, Bailleres H, Turner I, Perré P (2016) Characterisation of wood-water relationships and transverse anatomy and thier relationship to drying degrade. Wood Sci Technol 50:739–757

    Article  CAS  Google Scholar 

  • Rozsa A, Mills RG (1997) Index of kiln seasoning schedules. In: Waterson GC (ed) Australian timber seasoning manual, 3rd edn. Australian Furniture Research and Development Institute, Launceston, pp 167–175

    Google Scholar 

  • Salin JG (1991) Modeling of wood drying: a bibliography. Dry Technol 9(3):775–793

    Article  Google Scholar 

  • Salin JG (2010) Problems and solutions in wood drying modelling: history and future. Wood Mat Sci Eng 5:123–134

    Article  CAS  Google Scholar 

  • Salin JG (2011) Inclusion of the sorption hysteresis phenomenon in future drying models. Some basic considerations. Maderas Ciencia y tecnologia 13:173–182. doi:10.4067/s0718-221x2011000200005

    Article  Google Scholar 

  • Savard M, Lavoie V, Trembala C (2004) Technical and economical assessment of superheated steam vacuum drying of northern red oak. In: N.A.G.R.E.F. COST E15 conference, Athens, Greece, 22–24 April 2004. Forintek Canada Corp., pp 1–10

  • Siau JF (1984) Transport processes in wood. Springer, Berlin. doi:10.1007/978-3-642-69213-0

    Book  Google Scholar 

  • Turner IW, Perré P (2004) Vacuum drying of wood with radiative heating: II comparison between theory and experiment. AIChE J 50:108–118

    Article  CAS  Google Scholar 

  • Whitaker S (1977) Simultaneous heat, mass and momentum transfer in porous media: a theory of drying. Adv Heat Transf 13:119–203

    Article  CAS  Google Scholar 

  • Yu C, Cheng JJ, Zielen AJ (1991) Sensitivity analysis of the RESRAD, a dose assessment code. Trans Am Nucl Soc 64:73

    Google Scholar 

Download references

Acknowledgements

The substantial contributions of CentraleSupelec, Université Paris-Saclay, Queensland University of Technology (QUT), Forest and Wood Products Australia (FWPA) and the Queensland Government Department of Agriculture and Fisheries (DAF), to the undertaking of this collaborative project are gratefully acknowledged. Authors Turner and Carr wish to acknowledge that this research was partially supported by the Australian Research Council (ARC) via the Discovery Project DP150103675 and DECRA project DE150101137, respectively. Thank you to the reviewers for their comments and suggestions that led to an improved final version of the paper.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Science and Engineering Faculty, Queensland University of Technology (QUT), 2 George Street, GPO Box 2434, Brisbane, QLD, 4001, Australia

    Adam L. Redman, Elliot Carr & Ian Turner

  2. Agri-Science Queensland, Department of Agriculture and Fisheries, Queensland Government, 50 Evans Road, Salisbury, QLD, 4107, Australia

    Adam L. Redman & Henri Bailleres

  3. LGPM, CentraleSupelec, Université Paris-Saclay, Grande Voie des Vignes, 92 290, Châtenay-Malabry, France

    Patrick Perré

  4. Australian Research Council Centre of Excellence for Mathematical and Statistical Frontiers (ACEMS), Queensland University of Technology (QUT), Brisbane, Australia

    Ian Turner

Authors
  1. Adam L. Redman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Henri Bailleres
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Patrick Perré
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Elliot Carr
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ian Turner
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Adam L. Redman.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (DOCX 50 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Redman, A.L., Bailleres, H., Perré, P. et al. A relevant and robust vacuum-drying model applied to hardwoods. Wood Sci Technol 51, 701–719 (2017). https://doi.org/10.1007/s00226-017-0908-7

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00226-017-0908-7

Keywords

Search

Navigation