Skip to main content
SpringerLink
Log in

Uniformization of two-dimensional metric surfaces

  • Published:
Inventiones mathematicae Aims and scope

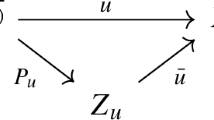
Abstract

We establish uniformization results for metric spaces that are homeomorphic to the Euclidean plane or sphere and have locally finite Hausdorff 2-measure. Applying the geometric definition of quasiconformality, we give a necessary and sufficient condition for such spaces to be QC equivalent to the Euclidean plane, disk, or sphere. Moreover, we show that if such a QC parametrization exists, then the dilatation can be bounded by 2. As an application, we show that the Euclidean upper bound for measures of balls is a sufficient condition for the existence of a 2-QC parametrization. This result gives a new approach to the Bonk–Kleiner theorem on parametrizations of Ahlfors 2-regular spheres by quasisymmetric maps.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ambrosio, L., Kirchheim, B.: Rectifiable sets in metric and Banach spaces. Math. Ann. 318, 527–555 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  2. Ambrosio, L., Tilli, P.: Topics on Analysis in Metric Spaces. Oxford University Press, Oxford (2004)

    MATH  Google Scholar 

  3. Astala, K., Bonk, M., Heinonen, J.: Quasiconformal mappings with Sobolev boundary values. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 1(3), 687–731 (2002)

    MathSciNet  MATH  Google Scholar 

  4. Azzam, J., Badger, M., Toro, T.: Quasiconformal planes with bi-Lipschitz pieces and extensions of almost affine maps. Adv. Math. 275, 195–259 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  5. Ball, K.: Volumes of sections of cubes and related problems. In: Geometric aspects of functional analysis (1987–1988), Lecture Notes in Math., 1376, pp. 251–260. Springer, Berlin (1989)

  6. Balogh, Z., Koskela, P., Rogovin, S.: Absolute continuity of quasiconformal mappings on curves. Geom. Funct. Anal. 17, 645–664 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Barthe, F.: Inégalités de Brascamp–Lieb et convexité. C. R. Acad. Scis. Paris 324, 885–888 (1997)

    Article  MATH  Google Scholar 

  8. Behrend, F.: Über einige Affininvarianten konvexer Bereiche. Math. Ann. 113(1), 713–747 (1937)

    Article  MathSciNet  MATH  Google Scholar 

  9. Bonk, M.: Quasiconformal geometry of fractals. In: International Congress of Mathematicians. vol. II, pp. 1349–1373. European Mathematical Society, Zürich (2006)

  10. Bonk, M.: Uniformization of Sierpinski carpets in the plane. Invent. Math. 186(3), 559–665 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  11. Bonk, M., Kleiner, B.: Quasisymmetric parametrizations of two-dimensional metric spheres. Invent. Math. 150(1), 127–183 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  12. Bonk, M., Kleiner, B.: Conformal dimension and Gromov hyperbolic groups with 2-sphere boundary. Geom. Topol. 9, 219–246 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  13. Bonk, M., Lang, U.: Bi-Lipschitz parametrization of surfaces. Math. Ann. 327(1), 135–169 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  14. Bonk, M., Merenkov, S.: Quasisymmetric rigidity of square Sierpinski carpets. Ann. Math. 177(2), 591–643 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  15. Bonk, M., Meyer, D.: Expanding Thurston maps. In: AMS Mathematical Surveys and Monographs (to appear) (2010)

  16. Cannon, J.W.: The combinatorial Riemann mapping theorem. Acta Math. 173, 155–234 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  17. David, G., Semmes, S.: Quantitative rectifiability and Lipschitz mappings. Trans. Am. Math. Soc. 337(2), 855–889 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  18. David, G., Toro, T.: Reifenberg flat metric spaces, snowballs, and embeddings. Math. Ann. 315(4), 641–710 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  19. Derrick, W.R.: Inequalities for \(p\)-modules of curve families on Lipschitz surfaces. Math. Z. 119, 1–10 (1971)

    Article  MathSciNet  MATH  Google Scholar 

  20. Derrick, W.R.: Extremal length and Rayleigh’s reciprocal theorem. Appl. Anal. 6(2):119–125 (1976/1977)

  21. Folland, G.B.: Real analysis: modern techniques and their applications. Wiley, New York (1984)

    MATH  Google Scholar 

  22. Fu, J.H.G.: Bi-Lipschitz rough normal coordinates for surfaces with an \(L^1\)-curvature bound. Indiana Univ. Math. J. 47(2), 439–453 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  23. Gehring, F.W.: Extremal length definitions for the conformal capacity of rings in space. Mich. Math. J. 9(2), 137–150 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  24. Gehring, F.W.: Lower dimensional absolute continuity properties of quasiconformal mappings. Math. Proc. Camb. Philos. Soc. 78, 81–93 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  25. Gehring, F.W.: Some metric properties of quasi-conformal mappings. In: Proceedings of the International Congress of Mathematicians (Vancouver B. C. 1974), vol. 2, pp. 203–206 (1975)

  26. Haïssinsky, P., Pilgrim, K.: Coarse expanding conformal dynamics, Astérisque, No. 325 (2009)

  27. Heinonen, J.: Lectures on analysis on metric spaces. Springer, New York (2001)

    Book  MATH  Google Scholar 

  28. Heinonen, J., Keith, S.: Flat forms, bi-Lipschitz parametrizations, and smoothability of manifolds. Publ. Math. Inst. Hautes Études Sci. 113(1), 1–37 (2011)

    Article  MATH  Google Scholar 

  29. Heinonen, J., Koskela, P.: Quasiconformal mappings in metric spaces with controlled geometry. Acta Math. 181, 1–61 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  30. Heinonen, J., Rickman, S.: Geometric branched covers between generalized manifolds. Duke Math. J. 113(3), 465–529 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  31. Heinonen, J., Semmes, S.: Thirty-three yes or no questions about mappings, measures, and metrics. Conform. Geom. Dyn. 1, 1–12 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  32. Heinonen, J., Sullivan, D.: On the locally branched Euclidean metric gauge. Duke Math. J. 114(1), 15–41 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  33. Heinonen, J., Wu, J.-M.: Quasisymmetric nonparametrization and spaces associated with the Whitehead continuum. Geom. Topol. 14(2), 773–798 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  34. Heinonen, J., Koskela, P., Shanmugalingam, N., Tyson, J.: Sobolev spaces on metric measure spaces: an approach based on upper gradients. In: New Mathematical Monographs, p. 27. Cambridge University Press, Cambridge (2015)

  35. Hurewicz, W., Wallman, H.: Dimension theory, Princeton Mathematical Series, vol. 4. Princeton University Press, Princeton (1941)

  36. Kirchheim, B.: Rectifiable metric spaces: local structure and regularity of the Hausdorff measure. Proc. Am. Math. Soc. 121(1), 113–123 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  37. Kleiner, B.: The asymptotic geometry of negatively curved spaces: uniformization, geometrization and rigidity, International Congress of Mathematicians. vol. II, pp. 743–768, European Mathematical Society, Zürich (2006)

  38. Laakso, T.: Plane with \(A_{\infty }\)-weighted metric not bilipschitz embeddable to \(R^n\). Bull. Lond. Math. Soc. 34, 667–676 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  39. Mattila, P.: Geometry of sets and measures in Euclidean spaces. Fractals and rectifiability. Cambridge Studies in Advanced Mathematics, vol. 44. Cambridge University Press, Cambridge (1995)

  40. Merenkov, S., Wildrick, K.: Quasisymmetric Koebe uniformization. Rev. Mat. Iberoam. 29(3), 859–909 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  41. Meyer, D.: Quasisymmetric embedding of self-similar surfaces and origami with rational maps. Ann. Acad. Sci. Fenn. Math. 27(2), 461–484 (2002)

    MathSciNet  MATH  Google Scholar 

  42. Meyer, D.: Snowballs are quasiballs. Trans. Am. Math. Soc. 362(3), 1247–1300 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  43. Moore, R.L.: Foundations of point set theory. American Mathematical Society Colloquium Publications, American Mathematical Society, Providence (1962)

  44. Müller, S., Šverák, V.: On surfaces of finite total curvature. J. Differ. Geom. 42(2), 229–259 (1995)

    MathSciNet  MATH  Google Scholar 

  45. Pankka, P., Wu, J.-M.: Geometry and quasisymmetric parametrization of Semmes spaces. Rev. Mat. Iberoam. 30(3), 893–970 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  46. Rado, T., Reichelderfer, P.V.: Continuous transformations in analysis. With an introduction to algebraic topology. Springer, Berlin (1955)

    MATH  Google Scholar 

  47. Schramm, O.: Transboundary extremal length (preprint version) (1993)

  48. Semmes, S.: Chord-arc surfaces with small constant. II. Good parametrizations. Adv. Math. 88, 170–199 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  49. Semmes, S.: Good metric spaces without good parametrizations. Rev. Mat. Iberoam. 12(1), 187–275 (1996)

    Article  MATH  Google Scholar 

  50. Semmes, S.: On the nonexistence of bi-Lipschitz parametrizations and geometric problems about \(A_{\infty }\)-weights. Rev. Mat. Iberoam. 12(2), 337–410 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  51. Semmes, S.: Finding curves on general spaces through quantitative topology, with applications to Sobolev and Poincaré inequalities. Sel. Math. (N.S.) 2, 155–295 (1996)

    Article  MATH  Google Scholar 

  52. Toro, T.: Surfaces with generalized second fundamental form in \(L^2\) are Lipschitz manifolds. J. Differ. Geom. 39(1), 65–101 (1994)

    MathSciNet  MATH  Google Scholar 

  53. Toro, T.: Geometric conditions and existence of bi-Lipschitz parametrizations. Duke Math. J. 77(1), 193–227 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  54. Tukia, P., Väisäl̈ä, J.: Quasisymmetric embeddings of metric spaces. Ann. Acad. Sci. Fenn. Ser. A I Math. 5(1), 97–114 (1980)

  55. Tyson, J.: Quasiconformality and quasisymmetry in metric measure spaces. Ann. Acad. Sci. Fenn. Ser. A I Math. 23, 525–548 (1998)

    MathSciNet  MATH  Google Scholar 

  56. Tyson, J.: Analytic properties of locally quasisymmetric mappings from Euclidean domains. Indiana Univ. Math. J. 49(3), 995–1016 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  57. Väisälä, J.: Lectures on \(n\)-dimensional quasiconformal mappings. Lecture Notes in Mathematics, vol. 229. Springer, Berlin, New York (1971)

  58. Väisälä, J.: Quasisymmetric embeddings in Euclidean spaces. Trans. Am. Math. Soc. 264(1), 191–204 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  59. Wildrick, K.: Quasisymmetric parametrizations of two-dimensional metric planes. Proc. Lond. Math. Soc. (3) 97(3), 783–812 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  60. Wildrick, K.: Quasisymmetric structures on surfaces. Trans. Am. Math. Soc. 362(2), 623–659 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  61. Williams, M.: Geometric and analytic quasiconformality in metric measure spaces. Proc. Am. Math. Soc. 140(4), 1251–1266 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  62. Ziemer, W.P.: Extremal length and conformal capacity. Trans. Am. Math. Soc. 126(3), 460–473 (1967)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

We are grateful to the anonymous referee for the careful reading of the manuscript and the thoughtful comments that lead to several improvements. We thank Mario Bonk, Changyu Guo, Jeff Lindquist, Dimitrios Ntalampekos, Martti Rasimus and Vyron Vellis for their comments and corrections.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, University of Jyväskylä, P.O. Box 35 (MaD), 40014, University of Jyväskylä, Finland

    Kai Rajala

Authors
  1. Kai Rajala
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kai Rajala.

Additional information

Research supported by the Academy of Finland, Project Number 257482. Parts of this research were carried out while the author was visiting the University of Michigan. He thanks the Department of Mathematics for hospitality.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rajala, K. Uniformization of two-dimensional metric surfaces. Invent. math. 207, 1301–1375 (2017). https://doi.org/10.1007/s00222-016-0686-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00222-016-0686-0

Mathematics Subject Classification

Search

Navigation