Abstract
The paper is devoted to the study of shock formation of the 3-dimensional quasilinear wave equation

where \(G^{\prime \prime }(0)\) is a non-zero constant. We will exhibit a family of smooth initial data and show that the foliation of the incoming characteristic hypersurfaces collapses. Similar to 1-dimensional conservational laws, we refer this specific type breakdown of smooth solutions as shock formation. Since \((\star )\) satisfies the classical null condition, it admits global smooth solutions for small data. Therefore, we will work with large data (in energy norm). Moreover, no symmetry condition is imposed on the initial datum. We emphasize the geometric perspectives of shock formation in the proof. More specifically, the key idea is to study the interplay between the following two objects: (1) the energy estimates of the linearized equations of \((\star )\); (2) the differential geometry of the Lorentzian metric \(g=-\frac{1}{(1+3G^{\prime \prime }(0) (\partial _t\phi )^2)} d t^2+dx_1^2+dx_2^2+dx_3^2\). Indeed, the study of the characteristic hypersurfaces (implies shock formation) is the study of the null hypersurfaces of g. The techniques in the proof are inspired by the work (Christodoulou in The Formation of Shocks in 3-Dimensional Fluids. Monographs in Mathematics, European Mathematical Society, 2007) in which the formation of shocks for 3-dimensional relativistic compressible Euler equations with small initial data is established. We also use the short pulse method which is introduced in the study of formation of black holes in general relativity in Christodoulou (The Formation of Black Holes in General Relativity. Monographs in Mathematics, European Mathematical Society, 2009) and generalized in Klainerman and Rodnianski (Acta Math 208(2):211–333, 2012).
Similar content being viewed by others
Notes
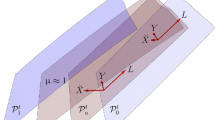
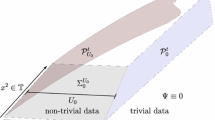
In a future work, we will consider a more general case for which the data is prescribed at past infinity. Therefore, we have to let \(r_0\) go to \(\infty \) and the dependence of the estimates (of the current work) on \(r_0\) will be crucial.
For a multi-index \(\alpha \), the symbol \(\alpha -1\) means another multi-index \(\beta \) with degree \(|\beta | = |\alpha |-1\).
This sentence always means that, there exists \(\varepsilon = \varepsilon (M)\) so that for all \(\delta \le \varepsilon \), we have ...
We emphasize that the trace \({\text {tr}}\) is defined with respect to g.
We emphasize that the traceless part of
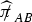 is defined with respect to
is defined with respect to 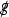 .
.The inequality is up to a constant depending only on the bootstrap constant M.
References
Alinhac, S.: Temps de vie des solutions régulières des équations d’Euler compressibles axisymétriques en dimension deux. Invent. Math. 111(3), 627–670 (1993)
Alinhac, S.: Blowup of small data solutions for a quasilinear wave equation in two space dimensions. Ann. Math. (2) 149(1), 97–127 (1999)
Alinhac, S.: Blowup of small data solutions for a class of quasilinear wave equations in two space dimensions. II. Acta Math. 182(1), 1–23 (1999)
Christodoulou, D.: The Action Principle and Partial Differential Equations. Annals of Mathematics Studies, vol. 146. Princeton University Press, Princeton, NJ (2000)
Christodoulou, D.: The Formation of Shocks in 3-Dimensional Fluids. Monographs in Mathematics. European Mathematical Society, Zürich (2007)
Christodoulou, D.: The Formation of Black Holes in General Relativity. Monographs in Mathematics. European Mathematical Society, Zürich (2009)
Christodoulou, D., Klainerman, S.: The Global Nonlinear Stability of Minkowski Space. Princeton Mathematical Series, vol. 41. Princeton University Press, Princeton, NJ (1993)
Christodoulou, D., Miao, S.: Compressible Flow and Euler’s Equations. (Monograph, 602 pp.). Surveys in Modern Mathematics, vol. 9. International Press, Somerville, MA; Higher Education Press, Beijing (2014)
Holzegel, G., Klainerman, S., Speck, J., Wong, W.: Shock Formation in Small-Data Solutions to \(3D\) Quasilinear Wave Equations: An Overview. J. Hyperbolic Differ. Equ. 13(1), 1–105 (2016)
John, F.: Blow-up of radial solutions of \(u_{tt}=c^2(u_t)\Delta u\) in three space dimensions. Mat. Apl. Comput. 4(1), 3–18 (1985)
John, F.: Nonlinear Wave Equations, Formation of Singularities. University Lecture Series, vol. 2. AMS, Providence (1990)
Klainerman, S.: Global existence for nonlinear wave equations. Commun. Pure Appl. Math. 33(1), 43–101 (1980)
Klainerman, S., Rodnianski, I.: On the formation of trapped surfaces. Acta Math. 208(2), 211–333 (2012)
Speck, J.: Shock formation in small-data solutions to \(3D\) quasilinear wave equations. arXiv:1407.6320v1 (preprint)
Acknowledgments
The authors are grateful to three anonymous referees, who carefully read a previous version of this paper and suggested many valuable improvements and corrections. S. Miao is supported by NSF Grant DMS-1253149 to The University of Michigan. P. Yu is supported by NSFC 11522111 and NSFC 11271219. The research of S. Miao was in its initial phase supported by ERC Advanced Grant 246574 “Partial Differential Equations of Classical Physics”.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Miao, S., Yu, P. On the formation of shocks for quasilinear wave equations. Invent. math. 207, 697–831 (2017). https://doi.org/10.1007/s00222-016-0676-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-016-0676-2



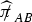 is defined with respect to
is defined with respect to 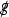 .
.