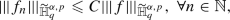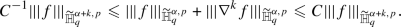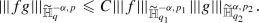Abstract
In this paper we show the existence of stochastic Lagrangian particle trajectory for Leray’s solution of 3D Navier–Stokes equations. More precisely, for any Leray’s solution \(\mathbf{u }\) of 3D-NSE and each \((s,x)\in \mathbb {R}_+\times \mathbb {R}^3\), we show the existence of weak solutions to the following SDE, which have densities \(\rho _{s,x}(t,y)\) belonging to \(\mathbb {H}^{1,p}_q\) with \(p,q\in [1,2)\) and \(\frac{3}{p}+\frac{2}{q}>4\):
where W is a three dimensional standard Brownian motion, \(\nu >0\) is the viscosity constant. Moreover, we also show that for Lebesgue almost all (s, x), the solution \(X^n_{s,\cdot }(x)\) of the above SDE associated with the mollifying velocity field \(\mathbf{u }_n\) weakly converges to \(X_{s,\cdot }(x)\) so that X is a Markov process in almost sure sense.
Similar content being viewed by others
References
Aizenman, M., Simon, B.: Brownian motion and Harnack inequaity for Schrödinger operators. Commun. Pure Appl. Math. 35, 209–273 (1982)
Bass, R.F., Chen, Z.Q.: Brownian motion with singular drift. Ann. Probabil. 31(2), 791–817 (2003)
Beck, L., Flandoli, F., Gubinelli, M., Maurelli, M.: Stochastic odes and stochastic linear pdes with critical drift: regularity, duality and uniqueness. Electron. J. Probabil. 24, 2019 (2019)
Buckmaster, T., Vicol, V.: Nonuniqueness of weak solutions to the Navier-Stokes equation. Ann. Math. 189(1), 101–144 (2019)
Chemin, J.Y., Lerner, N.: Flot de champs de vecteurs non lipschitziens et équations de Navier-Stokes. J. Differ. Equ. 121(2), 314–328 (1995)
Constantin, P., Iyer, G.: A stochastic Lagrangian representation of the three- dimensional incompressible Navier-Stokes equations. Commun. Pure Appl. Math. 61, 330–345 (2008)
Fedrizzi, E., Flandoli, F.: Noise prevents singularities in linear transport equations. J. Funct. Anal. 264, 1329–1354 (2013)
Flandoli, F., Gubinelli, M., Priola, E.: Well-posedness of the transport equation by stochastic perturbation. Invent. Math. 180, 1–53 (2010)
Flandoli, F., Issoglio, E., Russo, F.: Multidimensional stochastic differential equations with distributional drift. Trans. Am. Math. Soc. 369(3), 1665–1688 (2017)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (2015)
Hajaiej, H., Molinet, L., Ozawa, T., Wang, B.: Sufficient and necessary conditions for the fractional Gagliardo-Nirenberg inequalities and applications to Navier-Stokes and generalized Boson equations. RIMS Kokyuroku Bessatsu B26, 159–175 (2011)
Han, Q., Lin, F.: Elliptic Partial Differential Equations, vol. 1. American Mathematical Soc, London (2011)
Ikeda, N., Watanabe, S.: Stochastic differential equations and diffusion processes. North-Holland Mathematical Library, Vol.24. North-Holland Publishing Co., Amsterdam; Kodansha, Ltd., Tokyo (1989)
Kinzebulatov, D., Semënov, Y.A.: Brownian motion with general drift. Stochast. Process. Appl. 130(5), 2737–2750 (2020)
Krylov, N.V., Röckner, M.: Strong solutions of stochastic equations with singular time dependent drift. Probab. Theory Relat. Fields 131, 154–196 (2005)
Nazarov, A., Ural’tseva, N.N.: The Harnack inequality and related properties for solutions of elliptic and parabolic equations with divergence-free lower-order coefficients. St. Petersburg Math. J. 23(1), 93–115 (2012)
Portenko, N.I.: Generalized diffusion processes. Nauka, Moscow. In Russian; English translation: American Mathematical Society, Provdence, Rhode Island 1990 (1982)
Qian, Z., Xi, G.: Parabolic equations with divergence-free drift in space \(L_ {t}^{l} L_ {x}^{q}\). J. London Math. Soc. 100(2), 17–40 (2019)
Rezakhanlou, F.: Regular flows for diffusions with rough drifts. arXiv preprint arXiv:1405.5856 (2014)
Robinson, J.C., Rodrigo, J.L., Sadowski, W.: The Three-Dimensional Navier-Stokes Equations: Classical Theory. Cambridge University Press, Cambridge (2016)
Simon, J.: Compact sets in the space \(L^{p} ([0, T];B)\). Ann. Mat. Pura Appl. 146, 65–96 (1986)
Stein, E.M.: Singular integrals and differentiability properties of functions. Princeton Mathematical Series, No. 30. Princeton University Press, Princeton, NJ (1970)
Stroock, D.W., Varadhan, S.R.S.: Multidimensional Diffusion Processes, Grundlehren der Mathematischen Wissenschaften, 233. Springer, Berlin (1979)
Triebel, H.: Theory of function spaces II. Reprinted 2010 by Springer Basel AG
Veretennikov, A.: On the strong solutions of stochastic differential equations. Theory Probab. Appl. 24, 354–366 (1979)
Xi, G.: Parabolic equations and diffusion processes with divergence-free vector fields. Doctoral dissertation, University of Oxford (2018)
Zhang, X.: Stochastic homeomorphism flows of SDEs with singular drifts and Sobolev diffusion coefficients. Electron. J. Probab. 16, 1096–1116 (2011)
Zhang, X.: A stochastic representation for backward incompressible Navier-Stokes equations. Probab. Theory Relat. Fields 148, 305–332 (2010)
Zhang, X.: Stochastic flows of SDEs with irregular coefficients and stochastic transport equations. Bull. Sci. Math. France 134, 340–378 (2010)
Zhang, X.: Stochastic Lagrangian particle approach to fractal Navier-Stokes equations. Commun. Math. Phys. 311, 133–155 (2012)
Zhang, X.: Well-posedness and large deviation for degenerate SDEs with Sobolev coefficients. Rev. Mat. Iberoam. 29(1), 25–52 (2013)
Zhang, X.: Stochastic differential equations with Sobolev diffusion and singular drift. Ann. Appl. Probabil. 26(5), 2697–2732 (2016)
Zhang, X., Zhao, G.: Heat kernel and ergodicity of SDEs with distributional drifts. arXiv:1710.10537 (2017)
Zhang, X., Zhao, G.: Singular Brownian diffusion processes. Commun. Math. Stat. pp. 1–49 (2018)
Zvonkin, A.K.: A transformation of the phase space of a diffusion process that removes the drift. Mat. Sbornik 93(135), 129–149 (1974)
Acknowledgements
The authors would like to thanks two referees for their quite useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. Hairer
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research of X. Zhang is partially supported by NNSFC grant of China (No. 11731009). Research of G. Zhao is supported by the German Research Foundation (DFG) through the Collaborative Research Centre (CRC) 1283 “Taming uncertainty and profiting from randomness and low regularity in analysis, stochastics and their applications”.
Appendix: Properties of Space \(\widetilde{\mathbb {H}}^{\alpha ,p}_q\)
Appendix: Properties of Space \(\widetilde{\mathbb {H}}^{\alpha ,p}_q\)
In this “Appendix” we prove some important properties about the space \(\widetilde{\mathbb {H}}^{\alpha ,p}_q\). We need the following lemma, which can be found in [24, p.205] and [33, Lemma 2.2].
Lemma 4.1
-
(i)
For any \(\alpha \in {\mathbb {R}}\) and \(p\in (1,\infty )\), there is a \(C=C(d,\alpha ,p)>0\) such that
$$\begin{aligned} \Vert fg\Vert _{\alpha ,p}\leqslant C\Vert f\Vert _{\alpha ,p}\Vert g\Vert _{|\alpha |+1,\infty }. \end{aligned}$$(4.1) -
(ii)
Let \(p\in (1,\infty )\) and \(\alpha \in (0,1]\) be fixed. For any \(p_1\in [p,\infty )\) and \(p_2\in [\frac{p_1}{p_1-1},\infty )\) with \(\frac{1}{p}\leqslant \frac{1}{p_1}+\frac{1}{p_2}<\frac{1}{p}+\frac{\alpha }{d}\), there is a constant \(C>0\) such that for all \(f\in H^{-\alpha ,p_1}\) and \(g\in H^{\alpha ,p_2}\),
$$\begin{aligned} \Vert fg\Vert _{-\alpha ,p}\leqslant C \Vert f\Vert _{-\alpha ,p_1} \Vert g\Vert _{\alpha ,p_2}. \end{aligned}$$(4.2)
The following proposition shows that the localized norm  enjoys the almost same properties as the global norm \(\Vert \cdot \Vert _{\mathbb {H}^{\alpha ,p}_q}\).
enjoys the almost same properties as the global norm \(\Vert \cdot \Vert _{\mathbb {H}^{\alpha ,p}_q}\).
Proposition 4.1
Let \(p,q\in (1,\infty )\) and \(\alpha \in {\mathbb {R}}\).
-
(i)
For \(r\not =r'>0\), there is a constant \(C=C(d,\alpha ,r,r')\geqslant 1\) such that for all \(f\in \widetilde{\mathbb {H}}^{\alpha ,p}_q\),
$$\begin{aligned} C^{-1}\sup _{s,z}\Vert f\chi ^{s,z}_{r'}\Vert _{\mathbb {H}^{\alpha ,p}_q}\leqslant \sup _{s,z}\Vert f\chi ^{s,z}_r\Vert _{\mathbb {H}^{\alpha ,p}_q}\leqslant C \sup _{s,z}\Vert f\chi ^{s,z}_{r'}\Vert _{\mathbb {H}^{\alpha ,p}_q}. \end{aligned}$$(4.3)In other words, the definition of \(\widetilde{\mathbb {H}}^{\alpha ,p}_q\) does not depend on the choice of r.
-
(ii)
Let \((\rho _n)_{n\in {\mathbb {N}}}\) be a family of mollifiers in \({\mathbb {R}}^d\) and \(f_n(t,x):=f(t,\cdot )*\rho _n(x)\). For any \(f\in \widetilde{\mathbb {H}}^{\alpha ,p}_q\), it holds that \(f_n\in L^q_{loc}({\mathbb {R}}; C^\infty _b({\mathbb {R}}^d))\) and for some \(C=C(d,\alpha ,p,q)>0\),
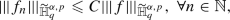 (4.4)
(4.4)and for any \(\varphi \in C^\infty _c({\mathbb {R}}^{d+1})\),
$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert (f_n-f)\varphi \Vert _{\mathbb {H}^{\alpha ,p}_q}=0. \end{aligned}$$(4.5) -
(iii)
For any \(k\in {\mathbb {N}}\), there is a constant \(C=C(d,k,\alpha ,p,q)\geqslant 1\) such that for all \(f\in \widetilde{\mathbb {H}}^{\alpha +k,p}_q\),
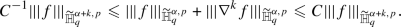
-
(iv)
Let \(p\in (1,\infty )\) and \(\alpha \in (0,1]\), \(q\in [1,\infty ]\). For any \(p_1\in [p,\infty )\) and \(p_2\in [\frac{p_1}{p_1-1},\infty )\) with \(\frac{1}{p}\leqslant \frac{1}{p_1}+\frac{1}{p_2}<\frac{1}{p}+\frac{\alpha }{d}\), and \(\frac{1}{q_1}+\frac{1}{q_2}=\frac{1}{q}\), there is a constant \(C>0\) such that
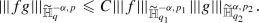
-
(v)
\(\mathbb {L}^p_q+\mathbb {L}^\infty _\infty \subsetneq \widetilde{\mathbb {L}}^p_q\).
Proof
-
(i)
Let \(r>r'\). We first prove the right hand side inequality in (4.3). Fix \((s,z)\in {\mathbb {R}}^{d+1}\). Notice that the support of \(\chi ^{s,z}_r\) is contained in \(Q^{s,z}_{2r}\). Clearly, \(Q^{s,z}_{2r}\) can be covered by finitely many \(Q_{r'}^{s_i,z_i}, i=1,\cdots , N\), where \(N=N(d,r,r')\) does not depend on s, z. Let \((\varphi _i)_{i=1}^{N}\) be the partition of unity associated with \(\{Q_{r'}^{s_i,z_i}, i=1,\cdots ,N\}\) so that
$$\begin{aligned} (\varphi _1+\cdots +\varphi _N)|_{Q^{s,z}_{2r}}=1,\ \mathrm{supp}(\varphi _i)\subset Q_{r'}^{s_i,z_i}. \end{aligned}$$Thus, due to \(\chi ^{s_i,z_i}_{r'}|_{Q_{r'}^{s_i,z_i}}=1\), by (4.1) we have
$$\begin{aligned} \Vert f\chi ^{s,z}_{r}\Vert _{\mathbb {H}^{\alpha ,p}_q}&\leqslant \sum _{i=1}^N\Vert f\chi ^{s,z}_{r}\varphi _i\Vert _{\mathbb {H}^{\alpha ,p}_q} =\sum _{i=1}^N\Vert f\chi ^{s_i,z_i}_{r'}\varphi _i\Vert _{\mathbb {H}^{\alpha ,p}_q}\\&\leqslant \sum _{i=1}^N\Vert f\chi ^{s_i,z_i}_{r'}\Vert _{\mathbb {H}^{\alpha ,p}_q}\Vert \varphi _i\Vert _{\mathbb {H}^{|\alpha |+1,\infty }_\infty } \leqslant C\sup _{i=1,\cdots , N}\Vert f\chi ^{s_i,z_i}_{r'}\Vert _{\mathbb {H}^{\alpha ,p}_q}, \end{aligned}$$where \(C=C(N,\alpha ,d,r,r')>0\), which yields the right hand side inequality in (4.3). On the other hand, since \(\chi ^{s,z}_{r'}=\chi ^{s,z}_{2r}\chi ^{s,z}_{r'}\), by what we have proved, we have
$$\begin{aligned} \Vert f\chi ^{s,z}_{r'}\Vert _{\mathbb {H}^{\alpha ,p}_q}=\Vert f\chi ^{s,z}_{2r}\chi ^{s,z}_{r'}\Vert _{\mathbb {H}^{\alpha ,p}_q} \leqslant C \Vert f\chi ^{s,z}_{2r}\Vert _{\mathbb {H}^{\alpha ,p}_q}\Vert \chi ^{s,z}_{r'}\Vert _{\mathbb {H}^{|\alpha |+1,\infty }_\infty }\leqslant C\Vert f\chi ^{s,z}_{r}\Vert _{\mathbb {H}^{\alpha ,p}_q}, \end{aligned}$$where C does not depend on s, z, which gives the left hand side inequality.
-
(ii)
By the definition of convolutions, it is easy to see that
$$\begin{aligned} (\chi ^{s,z}_1f_n)(t,x)=\chi ^{s,z}_1(t,x)\cdot (f\chi ^{s,z}_2)(t,\cdot )*\rho _n(x). \end{aligned}$$Hence,
$$\begin{aligned} \Vert \chi ^{s,z}_1f_n\Vert _{\mathbb {H}^{\alpha ,p}_q}\lesssim \Vert \chi ^{s,z}_1\Vert _{\mathbb {H}^{|\alpha |+1,\infty }_\infty }\Vert (f\chi ^{s,z}_2)_n\Vert _{\mathbb {H}^{\alpha ,p}_q} \lesssim \Vert \chi _1\Vert _{\mathbb {H}^{|\alpha |+1,\infty }_\infty }\Vert f\chi ^{s,z}_2\Vert _{\mathbb {H}^{\alpha ,p}_q}, \end{aligned}$$which gives (4.4). As for (4.5), it follows by a finitely covering technique.
-
(iii)
We only prove it for \(k=1\). By definition and \(\chi ^{s,z}_2\nabla \chi ^{s,z}_1=\nabla \chi ^{s,z}_1\) we have
$$\begin{aligned} \Vert (\nabla f) \chi ^{s,z}_1\Vert _{\mathbb {H}^{\alpha ,p}_q}&\leqslant \Vert \nabla (f \chi ^{s,z}_1)\Vert _{\mathbb {H}^{\alpha ,p}_q}+\Vert f \nabla \chi ^{s,z}_1\Vert _{\mathbb {H}^{\alpha ,p}_q}\\&\lesssim \Vert f \chi ^{s,z}_1\Vert _{\mathbb {H}^{\alpha +1,p}_q}+\Vert f\chi ^{s,z}_2\Vert _{\mathbb {H}^{\alpha ,p}_q}\Vert \nabla \chi ^{s,z}_1\Vert _{\mathbb {H}^{|\alpha |+1,\infty }_\infty }, \end{aligned}$$which in turn gives the right hand side estimate by (i). The left hand side inequality is similar.
-
(iv)
By (4.2) and \(\chi ^{s,z}_2\chi ^{s,z}_1=\chi ^{s,z}_1\), we have
$$\begin{aligned} \Vert (fg)\chi ^{s,z}_1\Vert _{\mathbb {H}^{-\alpha ,p}_q}=\Vert (f\chi ^{s,z}_2) (g\chi ^{s,z}_1)\Vert _{\mathbb {H}^{-\alpha ,p}_q} \leqslant \Vert f\chi ^{s,z}_2\Vert _{\mathbb {H}^{-\alpha ,p_1}_{q_1}} \Vert g\chi ^{s,z}_1\Vert _{\mathbb {H}^{\alpha ,p_2}_{q_2}}. \end{aligned}$$The desired estimate follows by (i).
-
(v)
Let \(\mathbb {Z}^d\) be the set of all lattice points. Define
$$\begin{aligned} f(t,x):=\mathbf{1}_{[0,1]}(t)\sum _{z\in \mathbb {Z}^d}|x-z|^{-d/p}\mathbf{1}_{|x-z|\leqslant 1}. \end{aligned}$$It is easy to see that \(f\in \widetilde{\mathbb {L}}^p_q\), but \(f\notin \mathbb {L}^p_q+\mathbb {L}^\infty _\infty \). \(\quad \square \)
Rights and permissions
About this article
Cite this article
Zhang, X., Zhao, G. Stochastic Lagrangian Path for Leray’s Solutions of 3D Navier–Stokes Equations. Commun. Math. Phys. 381, 491–525 (2021). https://doi.org/10.1007/s00220-020-03888-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-020-03888-w