Skip to main content
SpringerLink
Log in

Semiclassical Limit to the Vlasov Equation with Inverse Power Law Potentials

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

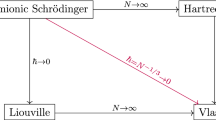
We consider mixed quasi-free states describing N fermions in the mean-field limit. In this regime, the time evolution is governed by the nonlinear Hartree equation. In the large N limit, we study the convergence towards the classical Vlasov equation. Under integrability and regularity assumptions on the initial state, we prove strong convergence in trace and Hilbert–Schmidt norm and provide explicit bounds on the convergence rate for a class of singular potentials of the form \({V(x)=|x|^{-\alpha}}\) , for \({\alpha\in(0,1/2)}\) .

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Amour L., Khodja M., Nourrigat J.: The semiclassical l imit of the time dependent Hartree–Fock equation: the Weyl symbol of the solution. Anal. PDE 6(7), 1649–1674 (2013)

    Article  MathSciNet  Google Scholar 

  2. Amour L., Khodja M., Nourrigat J.: The classical limit of the Heisenberg and time dependent Hartree–Fock equations: the Wick symbol of the solution. Math. Res. Lett. 20(1), 119–139 (2013)

    Article  MathSciNet  Google Scholar 

  3. Athanassoulis A., Paul T., Pezzotti F., Pulvirenti M.: Strong semiclassical approximation of Wigner functions for the Hartree dynamics. Rend. Lincei Mat. Appl. 22, 525–552 (2011)

    MathSciNet  MATH  Google Scholar 

  4. Bardos C., Degond P.: Global existence for the Vlasov–Poisson equation in 3 space variables with small initial data. Ann. Inst. H. Poincaré Anal. Non Linéaire 2, 101–118 (1985)

    Article  ADS  MathSciNet  Google Scholar 

  5. Benedikter N., Jaksic V., Porta M., Saffirio C., Schlein B.: Mean-field Evolution of Fermionic Mixed States. Commun. Pure Appl. Math. 69, 2250–2303 (2016)

    Article  MathSciNet  Google Scholar 

  6. Benedikter N., Porta M., Saffirio C., Schlein B.: From the Hartree–Fock dynamics to the Vlasov equation. Arch. Ration. Mech. Anal. 221(1), 273–334 (2016)

    Article  MathSciNet  Google Scholar 

  7. Benedikter N., Porta M., Schlein B.: Mean-field evolution of fermionic systems. Commun. Math. Phys. 331, 1087–1131 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  8. Dobrushin R.L.: Vlasov equations. Funct. Anal. Appl. 13(2), 115–123 (1979)

    Article  Google Scholar 

  9. Desvillettes L., Miot E., Saffirio C.: Polynomial propagation of moments and global existence for a Vlasov–Poisson system with a point charge. Ann. Inst. H. Poincaré (C) Anal. Non Linéaire 32(2), 373–400 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  10. Elgart A., Erdős L., Schlein B., Yau H.-T.: Nonlinear Hartree equation as the mean field limit of weakly coupled fermions. J. Math. Pures Appl. (9) 83(10), 1241–1273 (2004)

    Article  MathSciNet  Google Scholar 

  11. Evans, L.C.: Partial Differential Equations Graduate Studies in Mathematics, 19. American Mathematical Society, Providence (1998)

  12. Fefferman Ch.L., de la Llave R.: Relativistic stability of matter–I. Rev. Mat. Iberoam. 2(2), 119–213 (1986)

    Article  MathSciNet  Google Scholar 

  13. Figalli A., Ligabò M., Paul T.: Semiclassical limit for mixed states with singular and rough potentials. Indiana Univ. Math. J. 61(1), 193–222 (2012)

    Article  MathSciNet  Google Scholar 

  14. Gasser I., Illner R., Markowich P.A., Schmeiser C.: Semiclassical, \({t \to \infty}\) asymptotics and dispersive effects for HF systems. Math. Modell. Numer. Anal. 32, 699–713 (1998)

    Article  Google Scholar 

  15. Golse, F.: Mean field kinetic equations (2013). http://www.cmls.polytechnique.fr/perso/golse/M2/PolyKinetic.pdf

  16. Golse F., Paul T.: The Schrödinger equation in the mean-field and semiclassical regime. Arch. Ration. Mech. Anal. 223, 57–94 (2017)

    Article  MathSciNet  Google Scholar 

  17. Golse, F., Paul, T.: Empirical measures and quantum mechanics: applications to the mean-field limit. arXiv:1711.08350

  18. Golse, F., Pulvirenti, M., Paul, T.: On the derivation of the hartree equation in the mean field limit: uniformity in the planck constant. J. Funct. Anal. (To appear)

  19. Graffi S., Martinez A., Pulvirenti M.: Mean-field approximation of quantum systems and classical limit. Math. Models Methods Appl. Sci. 13(1), 59–73 (2003)

    Article  MathSciNet  Google Scholar 

  20. Hainzl C., Seiringer R.: General decomposition of radial functions on \({\mathbb{R}^n}\) and applications to N-body quantum systems. Lett. Math. Phys. 61(1), 75–84 (2002)

    Article  MathSciNet  Google Scholar 

  21. Holding, T., Miot, E.: Uniqueness and stability for the Vlasov–Poisson system with spatial density in Orlicz spaces. arXiv:1703.03046v1

  22. Iordanskii S.V.: The Cauchy problem for the kinetic equation of plasma. Trudy Mat. Inst. Steklov. 60, 181–194 (1961)

    MathSciNet  Google Scholar 

  23. Krylov, N.V.: Lectures on Elliptic and Parabolic Equations in Hölder Spaces, Graduate Studies in Mathematics AMS, vol. 12 (1996)

  24. Lieb E.H.: Thomas–Fermi and related theories of atoms and molecules. Rev. Mod. Phys. 53(4), 603–641 (1981)

    Article  ADS  MathSciNet  Google Scholar 

  25. Lieb, E.H., Loss, M.: Analysis: second edition. Graduate Studies in Mathematics, vol. 14. American Mathematical Society, Providence (2001). ISBN: 0-8218-2783-9

  26. Lieb E.H., Simon B.: The Thomas–Fermi theory of atoms, molecules and solids. Adv. Math. 23, 22–116 (1977)

    Article  MathSciNet  Google Scholar 

  27. Lions P.-L., Paul T.: Sur les mesures de Wigner. Rev. Mat. Iberoamericana 9, 553–618 (1993)

    Article  MathSciNet  Google Scholar 

  28. Lions P.-L., Perthame B.: Propagation of moments and regularity for the 3-dimensional Vlasov–Poisson system. Invent. Math. 105, 415–430 (1991)

    Article  ADS  MathSciNet  Google Scholar 

  29. Loeper G.: Uniqueness of the solution to the Vlasov–Poisson system with bounded density. J. Math. Pures Appl. (9) 86(1), 68–79 (2006)

    Article  MathSciNet  Google Scholar 

  30. Markowich P.A., Mauser N.J.: The classical limit of a self-consistent quantum Vlasov equation. Math. Models Methods Appl. Sci. 3(1), 109–124 (1993)

    Article  MathSciNet  Google Scholar 

  31. Miot E.: A uniqueness criterion for unbounded solutions to the Vlasov–Poisson system. Commun. Math. Phys. 345(2), 469–482 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  32. Narnhofer H., Sewell G.L.: Vlasov hydrodynamics of a quantum mechanical model. Commun. Math. Phys. 79(1), 9–24 (1981)

    Article  ADS  MathSciNet  Google Scholar 

  33. Okabe S., Ukai T.: On classical solutions in the large in time of the two-dimensional Vlasov equation. Osaka J. Math. 15, 245–261 (1978)

    MathSciNet  MATH  Google Scholar 

  34. Pallard C.: Moment propagation for weak solutions to the Vlasov–Poisson system. Commun. Partial Differ. Equ. 37(7), 1273–1285 (2012)

    Article  MathSciNet  Google Scholar 

  35. Pezzotti F., Pulvirenti M.: Mean-field limit and semiclassical expansion of a quantum particle system. Ann. H. Poincaré 10(1), 145–187 (2009)

    Article  MathSciNet  Google Scholar 

  36. Pfaffelmoser K.: Global existence of the Vlasov–Poisson system in three dimensions for general initial data. J. Differ. Equ. 95, 281–303 (1992)

    Article  ADS  MathSciNet  Google Scholar 

  37. Porta M., Rademacher S., Saffirio C., Schlein B.: Mean field evolution of fermions with Coulomb interaction. J. Stat. Phys. 166, 1345–1364 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  38. Saffirio, C.: Mean-field evolution of fermions with singular interaction. In: Cadamuro D., Duell M., Dybalski W., Simonella S. (eds.) Macroscopic limits of quantum systems. MaLiQS 2017. Springer Proceedings in Mathematics & Statistics, vol. 270, pp. 81–89. Springer, Cham (2018)

  39. Saffirio, C.: In preparation

  40. Sobolev, S.L.: On a theorem of functional analysis. Mat. Sb. (4) 46, 471–497 (1938) (translated into English in Transl. Amer. Math. Soc. 34, 39–68)

  41. Spohn H.: On the Vlasov hierarchy. Math. Methods Appl. Sci. 3(4), 445–455 (1981)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author is supported by the Grant SNSF Ambizione PZ00P2_161287/1.

Author information

Authors and Affiliations

  1. Institute of Mathematics, University of Zürich, Winterthurerstrasse 190, 8057, Zurich, Switzerland

    Chiara Saffirio

Authors
  1. Chiara Saffirio
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chiara Saffirio.

Additional information

Communicated by H. Spohn

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saffirio, C. Semiclassical Limit to the Vlasov Equation with Inverse Power Law Potentials. Commun. Math. Phys. 373, 571–619 (2020). https://doi.org/10.1007/s00220-019-03397-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-019-03397-5

Search

Navigation