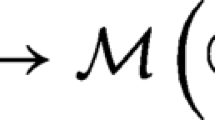Abstract
There are essentially two different approaches to the axiomatization of quantum field theory (QFT): algebraic QFT, going back to Haag and Kastler, and functorial QFT, going back to Atiyah and Segal. More recently, based on ideas by Baez and Dolan, the latter is being refined to “extended” functorial QFT by Freed, Hopkins, Lurie and others. The first approach uses local nets of operator algebras which assign to each patch an algebra “of observables”, the latter uses n-functors which assign to each patch a “propagator of states”.
In this note we present an observation about how these two axiom systems are naturally related: we demonstrate under mild assumptions that every 2-dimensional extended Minkowskian QFT 2-functor (“parallel surface transport”) naturally yields a local net, whose locality derives from the 2-categorical exchange law, and which is covariant if the 2-functor is equivariant. This is obtained by postcomposing the propagation 2-functor with an operation that mimics the passage from the Schrödinger picture to the Heisenberg picture in quantum mechanics. The argument has a straightforward generalization to general Lorentzian structure, bare lightcone structure and higher dimensions. It does not, however, by itself imply anything about the existence of a vacuum state or about positive energy representations.
Similar content being viewed by others
References
Abramsky, S., Coecke, B.: A categorical semantics of quantum protocols. In: Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS’04). IEEE Computer Science Press, 2004, pp. 415–425[arXiv:quant-ph/0402130]
Atiyah M.: Topological quantum field theory. Publ. Math. de l’IHÉS 68, 175–186 (1988)
Baas, N., Bökstedt, M., Kro, T.: Two-categorical bundles and their classifying spaces. http://arxiv.org/abs/math/0612549v2[math.AT], 2008
Baez, J.: Quantum quandaries: a category-theoretic perspective. In: Structural Foundations of Quantum Gravity, eds. S. French, D. Rickles, J. Saatsi, Oxford: Oxford U. Press, 2006, pp. 240–265
Baez J., Crans A.: Lie 2-algebras. Theor. Appl. of Categories 12, 492–528 (2004)
Baez J., Crans A., Schreiber U., Stevenson D.: From loop groups to 2-groups. Homology, Homotopy Appl. 9(2), 101–135 (2007)
Baez J., Dolan J.: Higher dimensional algebra and topological quantum field theory. J. Math. Phys. 36, 6073–6105 (1995)
Baez, J., Schreiber, U.: Higher gauge theory. In: Contemporary Mathematics 431, Categories in Algebra, Geometry and Mathematical Physics, Providence, RI: Amer. Math. Soc., 2007, pp. 7–30
Bartels, T.: 2-Bundles. PhD Thesis, UC Riverside, 2006, available at http://math.ver.edu/home/baez/thesis_toby.pdf
Bartlett, B.: Categorical aspects of topological quantum Field theories. M.Sc Thesis, Utrecht University, 2005, http://arxiv.org/abs/math/0512103v1[math.QA], 2005
Bartlett, B.: On unitary 2-representations of finite groups and TQFT. PdD Thesis, University of Sheffield, 2008
Brunetti R., Fredenhagen K., Verch R.: The generally covariant locality principle – A new paradigm for local quantum physics. Commun. Math. Phys. 237, 31–68 (2003)
Buchholz D., Haag R.: The quest for understanding in relativistic quantum physics. J. Math. Phys. 41, 3674–3697 (2000)
Cheng E., Gurski N.: Towards an n-category of cobordisms. Theory and Applications of Categories 18(10), 274–302 (2007)
Coecke, B.: Kindergarten quantum mechanics. Talk at Quantum Information, Computation and Logic (Perimeter Institute, 2005), available at http://www.quxat.org/quoxic.talks/bobkinder.pdf
Elgueta J.: Representation theory of 2-groups on Kapranov and Voevodsky’s 2-vector spaces. Adv. in Math. 213(1), 53–92 (2007)
Evans D.E., Kawahigashi Y.: Quantum symmetries on operator algebras. Oxford University Press, Oxford (1998)
Fjelstad J., Fuchs J., Runkel I., Schweigert C.: Uniqueness of open/closed rational CFT with given algebra of open states. Adv. Theor. Math. Phys. 12(6), 1283–1375 (2008)
Fjelstad, J., Schreiber, U.: Rational CFT is parallel transport, in preparation [http://www.math.uni-hamburg.de/home/schreiber/cc.pdf], 2008
Fredenhagen K., Rehren K., Seiler E.: Quantum field theory: Where we are. Lecture Notes in Physics 721, 61–87 (2007)
Freed D.S.: Higher algebraic structures and quantization. Commun. Math. Phys. 159, 343–398 (1994)
Freed, D.S.: Quantum groups from path integrals. Proceedings of Particles and Fields (Banff, 1994), 63Ð107, CRM Ser. Math. Phys., New York: Springer, 1999, available at http://arxiv.org/abs/q-alg/9501025v1, 1995
Freed D.S.: Remarks on Chern-Simons Theory. Bull. Amer. Math. Soc. (NS) 46(2), 221–254 (2009) [arXiv:0808.2507]
Ganter N., Kapranov M.: Representation and character theory in 2-categories. Adv. in Math. 213(1), 53–92 (2007)
Haag R.: Local Quantum Physics: Fields, Particles, Algebras. Springer, Berlin (1992)
Halvorson H., Mueger M.: Algebraic quantum field theory. In: Butterfield, J., Earman, J. (eds) Handbook of the Philosophy of Physics, pp. 731–922. North-Holland, Amsterdam (2007)
Lurie, J.: On the classication of topological field theories, [http://www-math.mit.edu/~lurie/papers/cobordism.pdf], 2009
Huang Y.-Z.: Geometric interpretation of vertex operator algebras. Proc. Natl. Acad. Sci. USA 88, 9964–9968 (1991)
Kapranov, M., Voevodsky, V.: 2-categories and Zamolodchikov tetrahedra equations. In: Algebraic Groups and Theor Generalization Quantum and Infinite-Dimension Methods, Proc. Symp. Pure Math. 56, Part 2, Providence, RI: Amer. Math. Soc., 1994, pp. 177–259
Kawahigashi, Y.: Classification of operator algebraic conformal field theories in dimensions one and two. In: Proceedings of XIV International Congress on Mathematical Physics at Lisbon (2003) [arXiv:math-ph/0308029]
Kawahigashi, Y.: Conformal Field Theory and Operator Algebras. In: Proceedings of ICMP, Rio de Janeiro (2006), available at http://arxiv.org/abs/0704.0097v1[math-ph], 2007
Kawahigashi, Y., Longo, R.: Classification of two-dimensional local conformal nets with c < 1 and 2-cohomology vanishing for tensor categories. 244, Number 1, 63–97 (2004)
Kelly, G.M.: Basic concepts of enriched category theory. Cambridge University Press, Lecture Notes in Mathematics 64, 1982; Republished in: Reprints in Theory and Applications of Categories, No. 10 (2005) pp. 1–136, available at http://www.tac.mta.ca/tac/reprints/articles/10/+10.pdf
Kawahigashi Y., Longo R.: Local conformal nets arising from framed vertex operator algebras. Adv. in Math. 206(2), 729–751 (2006)
Kong L.: Open-closed field algebras. Commun. Math. Phys. 280, 207–261 (2008)
Lauda A.: Frobenius algebras and ambidextrous adjunctions. Theory and Applications of Categories 16(4), 84–122 (2006)
Lechner, G.: On the construction of quantum field theories with factorizing S-Matrices. PhD thesis, Göttingen, 2006
Leinster, T.: Basic bicategories. http://arxiv.org/abs/math/9810017v2[math.CT], 1998
Longo R., Rehren K.-H.: Nets of subfactors. Rev. Math. Phys. 7, 567–597 (1995)
Longo R., Rehren K.-H.: Local fields in boundary conformal QFT. Rev. Math. Phys. 16, 909 (2004)
Müger M.: From subfactors to categories and topology I. Frobenius algebras in and Morita equivalence of tensor categories. J, Pure Appl. Alg. 180, 81–157 (2003)
Nill F., Szlachány K.: Quantum chains of Hopf algebras with order-disorder fields and quantum double symmetry. Commun. Math. Phys. 187(1), 159–200 (1997)
Ocneanu, A.: Quantized group, string algebras and Galois theory for algebras. In: Operator Algebras and Applications, Vol. 2, eds. Evans, D.E., Takesaki, M. Cambridge: Cambridge University Press, 1988, 119
Rehren, K.-H.: weblog comment, [http://golem.ph.utexas.edu/~distler/blog/archives/000987.html#c005396]
Roberts J., Longo R.: A theory of dimension. K-Theory 11(2), 103–159 (1997)
Runkel I., Fjelstad J., Fuchs J., Schweigert C.: Topological and conformal field theory as Frobenius algebras. Contemp. Math. 431, 225–248 (2007)
Sati, H., Schreiber, U., Škoda, Z., Stevenson, D.: Twisted nonabelian differential cohomology. In preparation, [http://www.math.uni-hamburg.de/home/schreiber/nactwist.pdf], 2008
Schreiber, U.: The canonical 2-representation. [http://www.math.uni-hamburg.de/home/schreiber/canrep.pdf], 2008
Schreiber, U., Waldorf, K.: Parallel transport and functors. To appear in Journal of Homotopy and Related Structures available at http://arxiv.org/abs/0705.0452v2[math.D6], 2008
Schreiber, U., Waldorf, K.: Smooth functors vs. differential forms. http://arxiv.org/abs0802.0663v2[math.DG], 2008
Schreiber, U., Waldorf, K.: Connections on non-abelian Gerbes and their Holonomy. http://arxiv.org/abs/0808.1923v1[math.DG], 2008
Schroer B.: Modular Wedge Localization and the d = 1 + 1 Formfactor Program. Annals Phys. 275, 190–223 (1999)
Segal, G.: The definition of conformal field theory. In: Topology, geometry and quantum field theory, London Math. Soc. LNS 308, edited by U. Tillmann, Cambridge: Cambridge Univ. Press 2004, pp. 247–343
Shulman M.: Framed bicategories and monoidal fibrations. Theory and Applications of Categories 20(18), 650–738 (2008)
Stolz, S., Teichner, P.: What is an elliptic object? In: Topology, geometry and quantum field theory, London Math. Soc. LNS 308, Cambridge: Cambridge Univ. Press, 2004, pp. 247–343
Street R.: Categorical and combinatorial aspects of descent theory. Applied Categorical Structures 12(5-6), 537–576 (2004)
Verity, D.: Cobordisms and weak complicial sets. Talk given at Macquarie Univ., Australian Category Theory Seminar, February 13, 2008
Walker, K.: TQFTs, [http://canyon23.net/math/tc.pdf]
Wockel, C.: A global perspective to gerbes and their gauge stacks. http://arxiv.org/abs/0803.3692v3[math.DG], 2008
Zito, P.: 2-C*-categories with non-simple units. PhD thesis, available at http://arxiv.org/abs/math/0509266v1, 2005
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Y. Kawahigashi
Rights and permissions
About this article
Cite this article
Schreiber, U. AQFT from n-Functorial QFT. Commun. Math. Phys. 291, 357–401 (2009). https://doi.org/10.1007/s00220-009-0840-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-009-0840-2