Skip to main content
SpringerLink
Log in

Random Matrices, Graphical Enumeration and the Continuum Limit of Toda Lattices

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

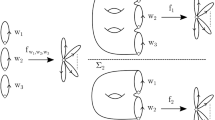
In this paper we derive analytic characterizations for and explicit evaluations of the coefficients of the matrix integral genus expansion. The expansion itself arises from the large N asymptotic expansion of the logarithm of the partition function of N × N Hermitian random matrices. Its g th coefficient is a generating function for graphical enumeration on Riemann surfaces of genus g. The case that we particularly consider is for an underlying measure that differs from the Gaussian weight by a single monomial term of degree 2ν. Our results are based on a hierarchy of recursively solvable differential equations, derived through a novel continuum limit, whose solutions are the coefficients we want to characterize. These equations are interesting in their own right in that their form is related to partitions of 2g + 1 and joint probability distributions for conditioned random walks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abramowitz, M., Stegun, I.: Handbook of Mathematical Functions. Washington, D.C.: U.S. Govt. Printing Office, 1972

  2. Ambjorn J., Chekhov L., Kristjansen C.F. and Makeenko Yu. (1993). Matrix Model Calculations Beyond the Spherical Limit. Nucl. Phys. B 404: 127–172

    Article  ADS  MathSciNet  Google Scholar 

  3. Albeverio S., Pastur L. and Shcherbina M. (2001). On the 1/n expansion for some unitary invariant ensembles of random matrices. Commun. Math. Phys. 224: 271–305

    Article  MATH  ADS  MathSciNet  Google Scholar 

  4. Bauer M. and Itzykson C. (1996). Triangulations. Discr. Math. 156: 29–81

    Article  MATH  MathSciNet  Google Scholar 

  5. Bessis D., Itzykson X. and Zuber J.B. (1980). Quantum Field Theory Techniques in Graphical Enumeration. Adv. Appl. Math. 1: 109–157

    Article  MATH  MathSciNet  Google Scholar 

  6. Bloch A., Golse F. and Uribe A. (2003). Dispersionless Toda and Toeplitz operators. Duke Math. J. 117: 157–196

    Article  MATH  MathSciNet  Google Scholar 

  7. Bouttier J., DiFrancesco P. and Guitter E. (2002). Census of Planar Maps: From the One-Matrix Model Solution to a Combinatorial Proof. Nucl. Phys. B 645: 477–499

    Article  MATH  ADS  MathSciNet  Google Scholar 

  8. Bleher P. and Its A. (2005). Asymptotics of the partition function of a random matrix model. Ann. Inst. Fourier (Grenoble) 55(6): 1943–2000

    MATH  MathSciNet  Google Scholar 

  9. Bousquet-Melou, M., Schaeffer, G.: The Degree Distribution in Bipartite Planar Maps: Applications to the Ising Model. http://arXiv.org/list/math.CO/0211070, 2002

  10. Deift P., Kriecherbauer T. and McLaughlin K.T.-R. (1998). New results on the equilibrium measure for logarithmic potentials in the presence of an external field. J. Approx. Thry. 95: 388–475

    Article  MATH  MathSciNet  Google Scholar 

  11. Deift P., Kriecherbauer T., McLaughlin K.T.-R., Venakides S. and Zhou X. (1999). Uniform asymptotics for polynomials orthogonal with respect to varying exponential weights and applications to universality questions in random matrix theory. Commun. Pure Appl. Math. 52(11): 1335–1425

    Article  MATH  MathSciNet  Google Scholar 

  12. Deift, P., McLaughlin, K.T.-R.: A Continuum Limit of the Toda Lattice. Memoirs of the AMS, 131 (624), January 1998

  13. Di Francesco P., Ginsparg P. and Zinn-Justin J. (1995). 2D gravity and random matrices. Phys. Rep. 254: 1–133

    Article  ADS  MathSciNet  Google Scholar 

  14. Dijkgraaf R., Verlinde E. and Verlinde H. (1991). Loop Equations and Virasoro Constraints in Non-perturbative Two-Dimensional Quantum Gravity. Nucl. Phys. B 348: 435–456

    Article  ADS  MathSciNet  Google Scholar 

  15. Ercolani N.M., Flaschka H. and Singer S. (1993). The Geometry of the Full Toda Lattice. Progress in Mathematics 115: 181–226

    MathSciNet  Google Scholar 

  16. Ercolani N.M. and McLaughlin K.D.T-R. (2003). Asymptotics of the partition function for random matrices via Riemann-Hilbert techniques and applications to graphical enumeration. Internat. Math. Research Notices 14: 755–820

    Article  MathSciNet  Google Scholar 

  17. Ercolani, N.M., McLaughlin, K.D.T-R.: A Quick Derivation of the Loop Equations for Random Matrices. To appear in Probability, Geometry and Integrable Systems, Cambridge University Press

  18. Erdélyi, A., Magnus, W., Oberhettinger, F., Tricomi, F.G.: Higher Transcendental Functions. Vol. 1. New York: Krieger, 1981, pp. 30–31

  19. Flascka H. (1974). On the Toda lattice. II. Inverse-scattering solution. Progr. Theoret. Phys. 51: 703–716

    Article  ADS  MathSciNet  Google Scholar 

  20. Flaschka, H.: Integrable Systems and Torus Actions. In: Lectures on Integrable Systems, eds. O. Babelon, P. Cartier, Y. Kosmann-Schwarzbach. London: World Scientific, pp. 43–101, 1994

  21. Geronimo J.S. and Case K.M. (1980). Scattering theory and polynomials orthogonal on the real line. Trans. Amer. Math. Soc. 258(2): 467–494

    Article  MATH  MathSciNet  Google Scholar 

  22. Johansson K. (1998). On fluctuations of eigenvalues of random hermitian matrices. Duke Math. J. 91(1): 151–204

    Article  MATH  MathSciNet  Google Scholar 

  23. Makeenko Y., Marshakov A., Mironov A. and Morozov A. (1991). Continuum versus Discrete Virasoro in One-Matrix Models. Nucl. Phys. B 356: 574–628

    Article  ADS  MathSciNet  Google Scholar 

  24. Mehta M.L. and Gaudin M. (1960). On the density of eigenvalues of a random matrix. Nucl. Phys. 18: 420–427

    Article  MathSciNet  Google Scholar 

  25. Mehta M.L. (1991). Random Matrices, 2nd edn. Academic Press, San Diego, CA

    MATH  Google Scholar 

  26. Pierce, V.: The asymptotic expansion of the partition function of random matrices. PhD Thesis, The University of Arizona, 2004

  27. Pierce, V.: Combinatoric Results to Planar Maps. http://arXiv.org/list/math.CO/0703160v1, 2007

  28. Pierce, V.: An Algorithm for Map Enumeration. http://arXiv.org/list/math.CO/0610586 , 2006

  29. Saff E.B. and Totik V. (1997). Logarithmic Potentials with External Fields. Springer-Verlag, New York

    MATH  Google Scholar 

  30. Szegő, G.: Orthogonal Polynomials, AMS Colloquium Publications, Vol. 23, Providence, RI: Amer. Math. Soc., 1939

  31. Witten, E.: Two-Dimensional Gravity and Intersection Theory on Moduli Space. In: Surveys in Differential Geometry, Vol 1, Boston: Ditl. Press, 1991, pp. 243–310

  32. Zvonkin A. (1998). How to Draw a Group. Discrete Math. 180: 403–413

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dept. of Math., Univ. of Arizona, Tucson, AZ, 85721, USA

    N. M. Ercolani & K. D. T-R. McLaughlin

  2. Dept. of Math., The Ohio State University, Columbus, OH, 43210, USA

    V. U. Pierce

Authors
  1. N. M. Ercolani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. D. T-R. McLaughlin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. U. Pierce
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. M. Ercolani.

Additional information

Communicated by M. Aizenman

K. D. T-R McLaughlin was supported in part by NSF grants DMS-0451495 and DMS-0200749, as well as a NATO Collaborative Linkage Grant “Orthogonal Polynomials: Theory, Applications, and Generalizations” Ref no. PST.CLG.979738.

N. M. Ercolani and V. U. Pierce were supported in part by NSF grants DMS-0073087 and DMS-0412310.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ercolani, N.M., McLaughlin, K.D.TR. & Pierce, V.U. Random Matrices, Graphical Enumeration and the Continuum Limit of Toda Lattices. Commun. Math. Phys. 278, 31–81 (2008). https://doi.org/10.1007/s00220-007-0395-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-007-0395-z

Keywords

Search

Navigation