Skip to main content
SpringerLink
Log in

Optimal Estimation of Qubit States with Continuous Time Measurements

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

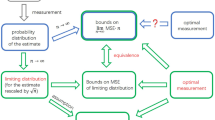
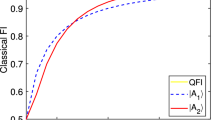
We propose an adaptive, two step strategy, for the estimation of mixed qubit states. We show that the strategy is optimal in a local minimax sense for the trace norm distance as well as other locally quadratic figures of merit. Local minimax optimality means that given n identical qubits, there exists no estimator which can perform better than the proposed estimator on a neighborhood of size n −1/2 of an arbitrary state. In particular, it is asymptotically Bayesian optimal for a large class of prior distributions.

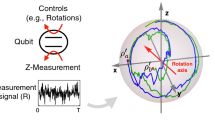
We present a physical implementation of the optimal estimation strategy based on continuous time measurements in a field that couples with the qubits. The crucial ingredient of the result is the concept of local asymptotic normality (or LAN) for qubits. This means that, for large n, the statistical model described by n identically prepared qubits is locally equivalent to a model with only a classical Gaussian distribution and a Gaussian state of a quantum harmonic oscillator. The term ‘local’ refers to a shrinking neighborhood around a fixed state ρ 0. An essential result is that the neighborhood radius can be chosen arbitrarily close to n −1/4. This allows us to use a two step procedure by which we first localize the state within a smaller neighborhood of radius n −1/2+ϵ, and then use LAN to perform optimal estimation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Artiles L., Gill R.D. and Guţă M. (2005). An invitation to quantum tomography. J. Royal Statist. Soc. B (Methodological) 67: 109–134

    Article  MATH  Google Scholar 

  2. Bagan E., Baig M. and Muñoz-Tapia R. (2002). Optimal Scheme for Estimating a Pure Qubit State via Local Measurements. Phys. Rev. Lett. 89: 277904

    Article  ADS  Google Scholar 

  3. Bagan E., Baig M., Muñoz-Tapia R. and Rodriguez A. (2004). Collective versus local measurements in a qubit mixed-state estimation. Phys. Rev. A 69: 010304(R)

    ADS  Google Scholar 

  4. Bagan E., Ballester M.A., Gill R.D., Monras A. and Muñoz-Tapia R. (2006). Optimal full estimation of qubit mixed states. Phys. Rev. A 73: 032301

    Article  ADS  Google Scholar 

  5. Bagan E., Monras A. and Muñoz-Tapia R. (2005). Comprehensive analysis of quantum pure-state estimation for two-level system. Phys. Rev. A 71: 062318

    Article  ADS  Google Scholar 

  6. Barndorff-Nielsen O.E., Gill R. and Jupp P.E. (2003). On quantum statistical inference (with discussion). J. R. Statist. Soc. B 65: 775–816

    Article  MATH  MathSciNet  Google Scholar 

  7. Barndorff-Nielsen O.E. and Gill R.D. (2000). Fisher information in quantum statistics. J. Phys. A 33: 1–10

    Article  ADS  MathSciNet  Google Scholar 

  8. Bouten L., Guţă M. and Maassen H. (2004). Stochastic Schrödinger equations. J. Phys. A 37: 3189–3209

    Article  MATH  ADS  MathSciNet  Google Scholar 

  9. Butucea C., Guţă M. and Artiles L. (2007). Minimax and adaptive estimation of the Wigner function in quantum homodyne tomography with noisy data. Ann. Stat 35(2): 465–494

    Article  MATH  Google Scholar 

  10. Caves C.M. (1982). Quantum limits on noise in linear amplifiers. Phys. Rev. D 26: 1817–1839

    Article  ADS  Google Scholar 

  11. Cirac J.I., Ekert A.K. and Macchiavello C. (1999). Optimal Purification of Single Qubits. Phys. Rev. Lett. 82: 4344

    Article  ADS  Google Scholar 

  12. D’Ariano G.M., Leonhardt U. and Paul H. (1995). Homodyne detection of the density matrix of the radiation field. Phys. Rev. A 52: R1801–R1804

    Article  ADS  Google Scholar 

  13. Dyson F.J. (1956). General Theory of Spin-Wave Interactions. Phys. Rev. 102: 1217–1230

    Article  MATH  ADS  MathSciNet  Google Scholar 

  14. Embacher F. and Narnhofer H. (2004). Strategies to measure a quantum state. Ann. of Phys. (N.Y.) 311: 220

    Article  MATH  ADS  MathSciNet  Google Scholar 

  15. Fisher D.G., Kienle S.H. and Freyberger M. (2000). Quantum-state estimation by self-learning measurements. Phys. Rev. A 61: 032306

    Article  ADS  Google Scholar 

  16. Fujiwara A. (2006). Strong consistency and asymptotic efficiency for adaptive quantum estimation problems. J. Phys. A 39: 12489–12504

    Article  MATH  ADS  MathSciNet  Google Scholar 

  17. Fujiwara A. and Nagaoka H. (1995). Quantum Fisher metric and estimation for pure state models. Phys. Lett. A 201: 119–124

    Article  MATH  ADS  MathSciNet  Google Scholar 

  18. Gardiner C.W. and Zoller P. (2004). Quantum Noise. Springer, Berlin-Heidelberg-New York

    MATH  Google Scholar 

  19. Geremia J., Stockton J.K. and Mabuchi H. (2004). Real-Time Quantum Feedback Control of Atomic Spin-Squeezing. Science 304: 270–273

    Article  ADS  Google Scholar 

  20. Gill, R.D.: Asymptotic information bounds in quantum statistics. http://arxiv.org/abs/math.ST/0512443, 2005, to appear in Annals of Statistics

  21. Gill R.D. and Massar S. (2000). State estimation for large ensembles. Phys. Rev. A 61: 042312

    Article  ADS  Google Scholar 

  22. Guţă M. and Kahn J. (2006). Local asymptotic normality for qubit states. Phys. Rev. A 73: 052108

    Article  ADS  MathSciNet  Google Scholar 

  23. Guţă, M., Jenčová, A.: Local asymptotic normality in quantum statistics, preprint quant-ph/0606213, to appear in Commun. Math. Phys

  24. Hannemann T., Reiss D., Balzer C., Neuhauser W., Toschek P.E. and Wunderlich C. (2002). Self-learning estimation of quantum states. Phys. Rev. A 65: 050303(R)

    Article  ADS  Google Scholar 

  25. Hayashi, M.: Presentations at MaPhySto and QUANTOP Workshop on Quantum Measurements and Quantum Stochastics, Aarhus, 2003, and Special Week on Quantum Statistics, Isaac Newton Institute for Mathematical Sciences, Cambridge, 2004

  26. Hayashi M. (2002). Two quantum analogues of Fisher information from a large deviation viewpoint of quantum estimation. J. Phys. A: Math. Gen. 35: 7689–7727

    Article  MATH  ADS  Google Scholar 

  27. Hayashi, M.: Quantum estimation and the quantum central limit theorem. Bull. Math. Soc. Japan 55, 368–391 (2003) (in Japanese; Translated into English in quant-ph/0608198)

    Google Scholar 

  28. Hayashi, M., editor: Asymptotic theory of quantum statistical inference: selected papers. River Edge, NJ: World Scientific, 2005

  29. Hayashi, M., Mastumoto, K.: Asymptotic performance of optimal state estimation in quantum two level system. http://arxive.org/list/quant-ph/0411073, 2001

  30. Hayashi, M., Matsumoto, K.: Statistical Model with Measurement Degree of Freedom and Quantum Physics. In: M. Hayashi, editor. Asymptotic theory of quantum statistical inference: selected papers, River Edge, NJ: World Scientific, 2005, pp. 162–170, (English translation of a paper in Japanese published in Surikaiseki Kenkyusho Kokyuroku 35, 7689-7727 (2002))

  31. Helstrom C.W. (1976). Quantum Detection and Estimation Theory. Academic Press, New York

    Google Scholar 

  32. Holevo, A.S.: Probabilistic and Statistical Aspects of Quantum Theory. Amsterdam: North-Holland, 1982

  33. Holtz R. and Hanus J. (1974). On coherent spin states. J. Phys. A 7: 37

    Article  ADS  Google Scholar 

  34. Hudson R.L. and Parthasarathy K.R. (1984). Quantum Itô’s formula and stochastic evolutions. Commun. Math. Phys. 93: 301–323

    Article  MATH  ADS  MathSciNet  Google Scholar 

  35. Janssens, B.: Unifying decoherence and the Heisenberg principle. http://arxiv.org/abs/quant-ph/0606093, 2006

  36. Jones K.R. (1994). Fundamental limits upon the measurement of state vectors. Phys. Rev. A 50: 3682

    Article  ADS  MathSciNet  Google Scholar 

  37. Kahn, J., Guţă, M., Matsumoto, K.: Local asymptotic normality for d-dimensional quantum states. in preparation

  38. Keyl M. and Werner R.F. (2001). Estimating the spectrum of a density operator. Phys. Rev. A 64: 052311

    Article  ADS  MathSciNet  Google Scholar 

  39. Latorre J.I., Pascual P. and Tarrach R. (1998). Minimal Optimal Generalized Quantum Measurements. Phys. Rev. Lett. 81: 1351

    Article  MATH  ADS  MathSciNet  Google Scholar 

  40. Le Cam L. (1986). Asymptotic Methods in Statistical Decision Theory. Springer Verlag, New York

    MATH  Google Scholar 

  41. Leonhardt U., Munroe M., Kiss T., Richter T. and Raymer M.G. (1996). Sampling of photon statistics and density matrix using homodyne detection. Optics Commun 127: 144–160

    Article  ADS  Google Scholar 

  42. Leonhardt U., Paul H. and D’Ariano G.M. (1995). Tomographic reconstruction of the density matrix via pattern functions. Phys. Rev. A 52: 4899–4907

    Article  ADS  Google Scholar 

  43. Mack H., Fischer D.G. and Freyberger M. (2000). Enhanced quantum estimation via purification. Phys. Rev. A 62: 042301

    Article  ADS  MathSciNet  Google Scholar 

  44. Massar S. and Popescu S. (1995). Optimal Extraction of Information from Finite Quantum Ensembles. Phys. Rev. Lett. 74: 1259–1263

    Article  MATH  ADS  MathSciNet  Google Scholar 

  45. Matsumoto K. (2002). A new approach to the Cramer-Rao type bound of the pure state model. J. Phys. A 35(13): 3111–3123

    Article  MATH  ADS  MathSciNet  Google Scholar 

  46. Nagaoka, H.: On the parameter estimation problem for quantum statistical models. In: M. Hayashi, editor. Asymptotic Theory of Quantum Statistical Inference, River Edge, NJ: World Scientific (2005), pp 125–132

  47. Schiller S., Breitenbach G., Pereira S.F., Müller T. and Mlynek J. (1996). Quantum statistics of the squeezed vacuum by measurement of the density matrix in the number state representation. Phys. Rev. Lett. 77: 2933–2936

    Article  ADS  Google Scholar 

  48. Smithey D.T., Beck M., Raymer M.G. and Faridani A. (1993). Measurement of the Wigner distribution and the density matrix of a light mode using optical homodyne tomography: Application to squeezed states and the vacuum. Phys. Rev. Lett. 70: 1244–1247

    Article  ADS  Google Scholar 

  49. Vaart A. (1998). Asymptotic Statistics. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  50. Wellner J. and Vaart A. (1996). Weak Convergence and Empirical Processes. Springer, New York

    MATH  Google Scholar 

  51. Vidal G., Latorre J.I., Pascual P. and Tarrach R. (1999). Optimal minimal measurements of mixed states. Phys. Rev. A 60: 126

    Article  ADS  Google Scholar 

  52. Vogel K. and Risken H. (1989). Determination of quasiprobability distributions in terms of probability distributions for the rotated quadrature phase. Phys. Rev. A 40: 2847–2849

    Article  ADS  Google Scholar 

  53. Wald A. (1943). Tests of Statistical Hypotheses Concerning Several Parameters When the Number of Observations is Large. Trans. Amer. Math. Soc. 54: 426–482

    Article  MATH  MathSciNet  Google Scholar 

  54. Werner R.F. (1998). Optimal cloning of pure states. Phys. Rev. A 58: 1827–1832

    Article  ADS  Google Scholar 

  55. Yuen H.P. and Lax M. (1973). Multiple-parameter quantum estimation and measurement of non-selfadjoint observables. IEEE Trans. Inform. Theory 19: 740

    Article  MATH  MathSciNet  Google Scholar 

  56. Zavatta A., Viciani S. and Bellini M. (2004). Quantum to classical transition with single-photon-added coherent states of light. Science 306: 660–662

    Article  ADS  Google Scholar 

  57. Zyczkowski K. and Sommers H.J. (2005). Average fidelity between random quantum states. Phys. Rev. A 71: 032313

    Article  ADS  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, University of Nottingham, University Park, Nottingham, NG7 2RD, UK

    Mădălin Guţă & Bas Janssens

  2. Département de Mathématiques, Université Paris-Sud 11, Bât 425, 91405, Orsay Cedex, France

    Jonas Kahn

Authors
  1. Mădălin Guţă
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bas Janssens
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jonas Kahn
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mădălin Guţă.

Additional information

Communicated by M.B. Ruskai

Rights and permissions

Reprints and permissions

About this article

Cite this article

Guţă, M., Janssens, B. & Kahn, J. Optimal Estimation of Qubit States with Continuous Time Measurements. Commun. Math. Phys. 277, 127–160 (2008). https://doi.org/10.1007/s00220-007-0357-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-007-0357-5

Keywords

Search

Navigation