Abstract
The experimental UV–Vis spectra of the biologically relevant [2Fe–2S] iron–sulfur clusters feature typically three bands in the 300–800 nm range. Based on ground-state orbitals and using the one electron transition picture, these bands are said to be of charge transfer character. The key complication in the electronic structure calculations of these compounds are the antiferromagnetic coupling of the iron centers and high covalency of Fe–S bonds. Thus, the examples of the direct computations of electronically excited states of these systems are rare. Whereas low lying electronic excited states were subject of recent studies, higher energy states computed with many-body theories were never reported. In this work we present, for the first time, calculations of the electronic spectra of [Fe2S2](SMe)2−4 biomimetic compound. We demonstrate that spin-averaged restricted open-shell Hartree–Fock orbitals are superior to high-spin orbitals and are convenient reference for subsequent configuration interaction calculations. Moreover, the use of conventional configuration interaction methods enabled us to study the nature of the excited states in details with the difference density maps. By systematic extension of the donor orbital space we show that key excitations in the 300–800 nm range are of Fe 3d ← (μ-S) character.
Similar content being viewed by others
1 Introduction
Iron–sulfur clusters are ubiquitous in nature. Their key biological role is to mediate the electron transfer (e.g. in hydrogenases [1]) but they also serve as the enzymatic reaction centers like in S-adenosyl-l-methionine reducing proteins that are involved in the DNA repair [2]. The clusters feature a core assembly of iron and sulfur atoms typically denoted as [FexSy]z, where x and y > 1 and z denotes the charge of the cluster, that is anchored to the protein scaffold with cysteine residues. Other linkers, such as histidine or aspartate, are also possible and were recently shown both experimentally [3] and theoretically [4] to influence the electronic properties of the clusters.
The key feature that makes the iron–sulfur clusters efficient electron mediators is the dense ladder of excited states that presumably allows the system to switch between them upon geometry change in a nonadiabatic process [5, 6]. Recently, light-induced charge-transfer (CT) pathways were spectroscopically characterized and a presence of long-lived CT states was confirmed [7, 8]. Based on a classical works on iron–sulfur clusters [9,10,11] that provide the analysis of a symmetry-broken (BS) ground state determinant of the Xα (or related) method, the CT state was attributed to Fe ← S(cysteine) excitation. We note, however, that the reasoning adapted is approximately valid only in a case of pure single electron transitions that may be characterized by a single pair of donor–acceptor orbitals. The key issue is that iron–sulfur clusters are known to posses unusually high density of states that is a consequence of low-spin, antiferromagnetic coupling between locally high-spin iron centers [12]. This property makes any quantum chemical calculations on iron–sulfur clusters very demanding as it requires proper treatment of the static correlation. Moreover, to the best of our knowledge, no UV–Vis spectra computed directly with a multiconfigurational approach was reported in the literature. The knowledge of the nature of states that are excited by the chosen wavelength (photoinduction, e.g. 400 nm) is prerequisite for a charge transfer dynamics analysis.
The usual approach, pioneered for iron–sulfur systems by Noodleman [9], involves the use of BS unrestricted wave function. It was shown later that the method provides good description of the low-spin ground state geometries and electronic properties of the iron–sulfur species [9,10,11, 13,14,15,16]. However, as the BS wave function is in fact a mixture of low- and higher-multiplicity states, the resulting BS determinant does not constitute good reference for the spin-adapted single reference correlated methods to describe the excited states.
The correct treatment of static correlation in iron–sulfur clusters requires at least a minimal complete active space (CAS) [17] consisting of all 3d orbitals of iron atoms and 3p orbitals of the bridging sulfurs. For a cluster with [Fe2S2]2+ core this yields an orbital space of 22 electrons distributed over 16 orbitals [CAS(22,16)]. For lowest possible spin state, such space is close to the limit of a canonical CAS self-consistent filed (CASSCF) calculations and still miss CT contributions from other ligands as well as dynamic correlation outside of the CAS is not covered.
The multireference character of the ground state wave function of the iron–sulfur clusters was first accounted for in an approximated way in the density matrix renormalization group (DMRG) study of Sharma et al. [18] that used minimal and extended CAS spaces for the analyzed systems. Authors computed first 10 excited states of [Fe2S2] and [Fe4S4] clusters with CH3S− ligands at various oxidation and spin states and found high density of low lying excited states. More recent work covered 20 excited states of the [Fe2S2](SMe)3−/2−4 system [19]. Interestingly, no ligand-to-metal CT states were found up to about 400 nm. DMRG was also employed to study even larger [Fe8S7] cluster (P-cluster of the nitrogenase) [20]. It was noted that the calculations become very demanding with increasing number of averaged states. Moreover, the wave function is prone to get stuck in a local minimum in the space of matrix product states, although these issues were partially alleviated with either applying exchange integrals shift [18] or by initiating the wave function with a complete collection of possible BS solutions for a given system [20].
[Fe2S2](SMe)3−/2−4 species were also subject of a restricted active space (RAS) study [21] of Presti et al. [22] In this case the reference space was partitioned into three sub-spaces: (1) 3p orbitals of the bridging sulfurs (RAS1), (2) 3d orbitals of the irons (RAS2) and (3) 3d’ orbitals that constitute the so-called second d shell (RAS3). Full configuration interaction was performed within the RAS2 space while only single excitations were allowed out of RAS1 or into RAS3. The dynamic correlation outside of the RAS was covered with the multiconfigurational pair-density functional approach [23]. Similarly to DMRG work [18], orbitals optimized at high-spin state were used to lower the computational cost. The main focus of the study was on the spin-state ladder and, interestingly, the ground spin state of [Fe2S2](SMe)3−4 was found to be high-spin.
In any case, the states reported to date for the simplest multimetallic iron–sulfur cluster model [Fe2S2](SMe)3−/2−4 cover excited states up to 25,000 cm−1 (3.1 eV, 400 nm). Some number of higher energy states were computed with RAS-based approach [22] but their nature was not analyzed. Thus, in this study we demonstrate economic computational strategy to compute and analyze the complete experimental UV–Vis spectra of the oxidized [Fe2S2](SMe)2−4 model iron–sulfur cluster for which the experimental data are available [24]. Our approach focus on obtaining best low-spin orbitals that can be used as a reference in a multireference configuration interaction (CI) scheme within the active space. We demonstrate, that spin-averaged Hartree–Fock (SAHF) method provides good orbitals for CI treatment of charge-transfer excited states. While only limited number of states can be computed at low-spin state, we show that by virtue of intrinsic electronic properties of iron–sulfur clusters the nature of key CT states can be approximated by assuming ferromagnetic coupling (total high spin). The use of canonical CI methods enables computations of oscillator strengths for obtained electronic transitions and allows to compare theoretical electronic spectrum with the measured UV–Vis spectrum. The key outcome is that we found excellent agreement between the two and point out that the spectrum is mainly due to Fe ← (μ-S) CT transitions and Fe ← S(cysteine) excitations can only be observed above 300 nm.
2 Methods
All electronic structure calculations were carried out with ORCA 4.2.0 program [25]. Multiwfn [26] was used to carry out cube files manipulations. Visualizations were performed with VMD 1.9.0 [27].
The geometry of the [Fe2S2](SMe)2−4 molecule was optimized within the density functional theory using BP86 functional [28, 29] augmented with the D3BJ dispersion correction [30, 31]. The ground electronic state has antiferromagnetic character (total spin of 0 with locally high-spin 3d5 iron atoms) and it was simulated with the broken symmetry approach. From a technical point of view, orbital preparation is a three-step procedure that uses localized natural orbitals: [4, 32] (1) first the high spin natural orbitals (NOs) state (multiplicity 11) orbitals are obtained, then (2) the singly occupied NOs are localized and duplicated into the alpha and beta sets providing the Fe-localized 3d orbitals of different iron atoms are placed in different sets so that (3) subsequent low spin (multiplicity 1) unrestricted calculations converge smoothly to the BS state. The optimized geometry was subject to second derivative calculations and all normal modes were positive (local energy minimum). Cartesian coordinates of the structure can be found in the Supplementary Information.
Unrestricted high-spin Kohn–Sham BP86 orbitals of the low-spin optimized geometry were fed into the unrestricted Hartree–Fock (UHF) calculations to generate UHF quasi-restricted orbitals (QROs) [33] that are good starting point in the spin-restricted calculations. The spin-averaged Hartree–Fock (SAHF) [34] calculations were set to average all states of multiplicity 1 resulting from the distribution of 10 electrons over 10 singly occupied QROs. The final orbital set was subject to orbital localization with Pipek-Mezey approach [35]. Doubly occupied and singly occupied sets were localized separately. Resulting orbitals were then sorted according to visual inspection so that four principal sets were formed: (1) ten orbitals of mainly iron 3d character (2) six μ-S 3p orbitals (3) four σ-S(cysteine) bonding orbitals of mainly S 3p character and (4) four n-S(cysteine) 3p orbitals that accommodate the lone pair. The orbitals are depicted in Fig. 1. For comparison, analogous procedure was followed for simple high-spin ROHF reference.
Obtained SAHF orbitals were used in the CASCI calculations with the active space comprising of orbitals from sets (1) and (2) what resulted in a (22,16) space (22 electrons and 16 orbitals). Additional RASCI calculations included also orbitals from sets (3) and (4) by allowing single excitations into the RAS2 (16 orbitals, essentially full CI) out of the RAS1 space (8 orbitals). In RASCI calculations 38 electrons were correlated and the full calculations are denoted as RAS(38: 8 1/16). Computed spectra were plotted with 2000 cm−1 broadening and were shifted by − 6000 cm−1 to visually match with the experimental spectrum. Such shift does not affect the shape of the spectrum and accounts for systematic errors of the method. Unshifted absolute excitation energies for various wave functions considered are provided in the Supplementary Information.
The nature of the excited states was analyzed by first forming the state-specific natural orbitals for all excited states. In the next step, state-specific electronic densities were generated on a grid and saved as cube files with orca_plot utility program that is part of the ORCA system. Final density differences were obtained by taking the difference between ground state electron density and the chosen excited state electron density.
All calculations reported employed def2-TZVP basis set [36]. Whenever implemented, resolution of identity (RI) approximation [37, 38] was used to ease Coulomb integrals evaluations while chain-of-spheres approximation (COSX) [39] was applied to the exchange integrals. These calculations utilized def2-TZVP/J (HF or DFT) or def2-TZVP/C (CI methods) auxiliary basis sets [40].
3 Results
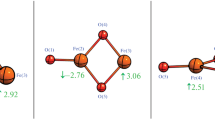
In the optimized geometry, the Fe–Fe interatomic distance was 2.63 Å and (μ-S1)-Fe-(μ-S2) angle was 106°. All four Fe–S(cysteine) bond lengths were found to be 2.32 Å while iron-inorganic sulfur bonds were shorter (2.19 Å). Obtained data are consistent with synthetic [2Fe–2S] clusters as well as those found in proteins [41].
SAHF orbitals optimization on the top of BP86 geometry yielded orbitals shown in Fig. 1. We note that SAHF procedure yields virtually the same orbitals as CASSCF method with maximal number of roots for a given multiplicity and initial orbital space. We confirm the equivalence by computing the total SAHF and state-averaged CASSCF (5 states) energies of high-spin Fe2+ ion with the active space of 5 3d orbitals and 6 associated electrons. Total energy of − 1261.630285 a.u. was found in both cases. The key difference is that for SAHF averaging occurs at the level of energy expression so that only total averaged energy is computed while in the CASSCF method averaged are electronic states and CI matrix eigenvalues are readily available. In the latter case, the formation of spin-adapted states limits the practical applications of the method.
In our scheme, to access the excited states manifold, we performed multi-root multireference CI calculations on the top of SAHF orbitals within the active space orbitals shown in Fig. 1. In this case the singly occupied set (SOMOs) is mainly of Fe 3d character but the Fe–S covalency is significant owing large delocalization onto sulfur atoms. The orbitals were then subject to CASCI(22,16) calculations and all bridging S 3p and SOMOs were included in the active space. The computed UV–Vis spectra are shown in Fig. 2.
Comparison of experimental (black) and computed UV–Vis electronic absorption spectra of Fe2S2](SMe)2−4 The active space in CASCI calculations was always (22,16) and SAHF reference orbitals (multiplicity 1) were used. The spin state and the number of states accounted in the target CASCI wave function is indicated in the legend
In the first step, CASCI(22,16) calculations were performed by solving the CI problem for 50 roots (red line in Fig. 2). State with energy of 18,245 cm−1 was identified and associated with experimentally observed transition about 18,000 cm−1. Attempts to obtain higher number of roots (e.g. 100) failed as the residual norm of higher-energy roots oscillated significantly and did not converge. However, we observed that the same calculations but with spin state set to 5 in CASCI step yielded spectrum that up to 20,000 cm−1 resembles the low spin spectrum (blue line in Fig. 2). Interestingly, the two bands around 21,000 and 24,000 cm−1 were reproduced. By further increasing the number of roots to 100 (green line in Fig. 2) and 200 (gray line in Fig. 2) we were able to qualitatively cover the spectrum up to 35,000 cm−1. Beyond this energy, the agreement was not that good and two maxima were obtained in theory while single maximum of high intensity was observed in the experimental spectrum.
The striking overlap of energies of the state responsible for the band around 18,000 cm−1 computed at high- and low-spin states prompted us to investigate this phenomenon more in details. Inspection of the differential electron density provided in Fig. 3 revealed that the state is of CT character: the electrons are excited from the Fe-(μ-S) bonds to a Fe 3d orbitals. Why then the excitation energy does not depend on the spin of the wave function? To answer this question we analyzed two selected determinants from a simple three orbital—four electron system (Fig. 4). First determinant represents an open-shell singlet case (Fig. 4a) while the second is a classical triplet (Fig. 4b). Both determinants are assumed to share the same spatial orbitals that are spatially separated. The double occupied spin-orbital (2) represents donor ligand orbital (e.g. 3p S) and two SOMOs (1) and (2) form the magnetic pair. The energy difference ΔES-T between the ground state determinants is proportional to the exchange integral between magnetic orbitals (K23). We also consider corresponding single exited states and here the energy difference is proportional to K13. Excitation energy in the case of open-shell singlet is proportional to combination of Coulomb integrals only. On the other hand, excitation out of the triplet determinant has an exchange component (− K23 + K12). If the latter is close to 0 then the excitation energy would not depend on the spin state used in calculations. This will happen either in case of K12 ≈ K23 or when simultaneously the magnitude of K12 and K23 is small. We note that we assumed the spin orbitals (1), (2) and (3) to be spatially well separated. Exchange interactions fall quickly with the distance so that we can expect K12 and K23 to be small. In the real system Fe…Fe exchange interaction must necessarily be small as the spins on two iron centers tend to align antiferromagnetically. Indeed, inspection of exchange integrals over orbitals centered on different iron atoms shows that they are small, on the order of 0.001 a.u.. To put this number into a perspective, Coulomb integrals for the same orbitals are ~ 0.2 a.u. while exchange integrals that involve orbitals centered on the same atom are roughly around 0.01 a.u. Exchange integrals between iron atom and μ-S 3p orbitals falls in range between 0.01 and 0.001 a.u. Thus, the iron–sulfur cluster fulfills simultaneously both requirements for excitation energy being insensitive to the spin state used in calculations (low- or high-spin): exchange interactions between magnetic centers is small and comparable in magnitude to exchange interactions between 3d electrons of iron and 3p electrons of sulfurs. We note, that such equivalence would not hold for intermediate spin-states that involve local Fe excitations.
Analysis of energies and energy differences between selected determinants representing open-shell singlet (a) and triplet (b) states arising in a simple three orbital—four electron system. Both spin states are assumed to share the same spatial orbitals. J and K are Coulomb and exchange integrals, respectively; subscripts denote spin orbitals
With an established successful protocol for UV–Vis spectrum simulations up to 35,000 cm−1 one has to deal with even higher energy features in the experimental spectrum that are not that well reproduced. Earlier studies suggested possible CT states closer to 25,000 cm−1 that result from Fe ← S(cysteine) transitions. To investigate these possibilities we extended our CASCI(22,16) to RASCI(38: 8 1/16) approach, also with a high-spin state. Here, the previous CAS space constitutes the so-called RAS2 space in which essentially the full CI calculation is performed. This space is supplemented with additional set of orbitals called RAS1 and only single excitations are allowed out of RAS1 into the RAS2. The essential physics should be then covered—CT states of Fe ← S(cysteine) character will be generated, multireference character will be accounted for and simultaneously the RAS2 excitations will be polarized by the cysteinyl ligands. We also note that trial calculations shows that orbitals associated with inorganic sulfur atoms must necessarily be part of the RAS2 and cannot be moved to RAS1 as each computed state is comprised of multiple number of configuration state functions of small weight (< 0.02) where the hole is placed on any of the six sulfur-centered orbitals.
The results of the calculations are presented in the Fig. 5. It is clear that extended orbital space does not alter the lower energy spectrum. In the region above 35,000 cm−1 a significant changes were noted due to presence of expected Fe ← S(cysteine) excited states. On the basis of the differential density plots derived from RASCI calculations (see Fig. 5b) we can make final experimental band assignment in a following way:
-
1.
~ 13,000 cm−1: low intensity Fe 3d ← n-(μ-S) coupled with local Fe 3d excitations
-
2.
~ 18,000 cm−1: Fe 3d(e.g.) ← σ*-(μ-S)
-
3.
~ 21,000 and 25,000 cm−1: Fe 3d(e.g.) ← σ-(μ-S)
-
4.
~ 30,000 cm−1: Fe 3d(t2) ← (μ-S)
-
5.
~ 36,000 cm−1: Fe 3d ← n-S(cysteine)
-
6.
~38,000 cm−1: Fe 3d ← σ-S(cysteine)
In the classification, we used σ and σ* to denote 3p atomic orbitals that form binding and antibonding pairs with iron 3d orbitals, respectively; 3d orbitals were classified using Td point group whenever possible.
4 Summary
In this work for the first time the high energy UV–Vis spectrum was simulated using multireference approach. Up to 35,000 cm−1 the spectrum was found to have exclusively Fe 3d ← (μ-S) character with marked features that come from inorganic sulfur lone pairs as well as from Fe–S σ and σ* orbitals. The postulated Fe ← S(cysteine) charge transfer states were found in higher energies. The latter means that only little to none of them would be accessible with 400 nm excitation light. However, thermal vibrations and potential created by the protein may shift these state lower in energy. Such shift will be investigated in an upcoming work.
From a methodological point of view, we pointed out that special electronic properties of the iron–sulfur clusters (small exchange interaction between Fe atoms as well as between iron and sulfurs) allow to compute and characterize CT excited states by using high-spin CI approach. However, the use of low-spin orbitals is mandatory. We have shown that SAHF method provides excellent orbital basis for subsequent CI treatment of the excited states. In contrary, high-spin ROHF orbitals are not suitable for the present method—the first excited state is found > 55,000 cm−1 (unshifted) and the spectrum does not show proper band structure. In a broader perspective, we believe that SAHF reference should be tested in schemes that approximate true multireference wave functions such as DMRG. It may happen that the orbital space would be more compact as compared to high-spin reference. In this way computations on even larger iron–sulfur clusters or clusters that feature additional hetero atom may become accessible.
References
Lubitz W, Ogata H, Rüdiger O, Reijerse E (2014) Chem Rev 114:4081–4148
Fuss JO, Tsai CL, Ishida JP, Tainer JA (2015) Biochim Biophys Acta Mol Cell Res 1853:1253–1271
Dementin S, Burlat B, Fourmond V, Leroux F, Liebgott PP, Abou Hamdan A, Léger C, Rousset M, Guigliarelli B, Bertrand P (2011) J Am Chem Soc 133:10211–10221
Kubas A, Maszota P (2018) Eur J Inorg Chem 2018:2419–2428
Voityuk AA (2010) Chem Phys Lett 495:131–134
Teo RD, Rousseau BJG, Smithwick ER, Di Felice R, Beratan DN, Migliore A (2019) Chem 5:122–137
Mao Z, Carroll EC, Kim PW, Cramer SP, Larsen DS (2017) J Phys Chem Lett 8:4498–4503
Mao Z, Liou SH, Khadka N, Jenney FE Jr, Goodlin DB, Seefeldt LC, Adams MWW, Cramer SP, Larsen DS (2018) Biochemistry 57:978–990
Norman J, Ryan P, Noodleman L (1980) J Am Chem Soc 102:4279–4282
Aizman A, Case DA (1982) J Am Chem Soc 104:3269–3279
Noodleman L, Baerends EJ (1984) J Am Chem Soc 106:2316–2327
Beinert H, Holm RH, Mück E (1997) Science 277:653–659
Noodleman L, Norman JG, Osborne JH, Aizman A, Case DA (1985) J Am Chem Soc 107:3418–3426
Noodleman L, Case DA, Aizman A (1985) J Am Chem Soc 110:1001–1005
Bergeler M, Striebritz MT, Reiher M (2013) ChemPlusChem 2013:1082–1098
Finkelmann AR, Striebritz MT, Reiher M (2014) Inorg Chem 2014:11890–11902
Roos BO, Taylor PR, Siegbahn PEM (1980) Chem Phys 48:157–173
Sharma S, Sivalingam K, Neese F, Chan GKL (2014) Nat Chem 6:927–933
Cho D, Rouxel JR, Mukamel S, Chan GKL, Li Z (2019) J Phys Chem Lett 10:6664–6671
Li Z, Guo S, Sun Q, Chan GKL (2019) Nat Chem 11:1026–1033
Malmqvist PÅ, Rendell A, Roos BO (1990) J Phys Chem 94:5477–5482
Presti D, Stoneburner SJ, Truhlar DG, Gagliardi L (2019) J Phys Chem C 123:11899–11907
Li Manni G, Carlson RK, Luo S, Ma D, Olsen J, Truhlar DG, Gagliardi L (2014) J Chem Theory Comput 10:3669–3680
Hagen KS, Watson AD, Holm RH (1983) J Am Chem Soc 105:3905–3913
Neese F (2018) WIRes: comp. Mol. Sci. 8:e1327
Lu T, Chen F (2012) J Comp Chem 33:580–592
Humphrey W, Dalke A, Schulten K (1996) J Mol Graph 14:33–38
Perdew JPP (1986) Phys Rev B 33:8822–8824
Becke AD (1988) Phys Rev A 38:3098–3100
Grimme S, Antony J, Ehrlich S, Krieg H (2010) J Chem Phys 132:154104
Grimme S, Ehrlich S, Goerigk L (2011) J Comput Chem 32:1456–1465
Shoji M, Yoshioka Y, Yamaguchi K (2014) Chem Phys Lett 608:50–54
Neese F (2006) J Am Chem Soc 128:10213–10222
Stavrev KK, Zerner MC (1997) Int J Quant Chem 65:877–884
Pipek J, Mezey PG (1989) J Chem Phys 90:4916–4926
Weigend F, Ahlrichs R (2005) Phys Chem Chem Phys 7:3297–3305
Eichkorn K, Treutler O, Öhm H, Häser M, Ahlrichs R (1995) Chem Phys Lett 242:652–660
Eichkorn K, Weigend F, Treutler O, Ahlrichs R (1997) Theor Chem Acc 97:119–124
Izsák R, Neese F (2011) J Chem Phys 135:144105
Weigend F (2006) Phys Chem Chem Phys 8:1057–1065
Venkateswara Rao P, Holm RH (2004) Chem Rev 104:527–560
Acknowledgements
This work was supported by the National Science Centre, Poland (NCN) under Grant no. 2015/17/D/ST4/00112. Access to high performance computing resources was provided by the Interdisciplinary Centre for Mathematical and Computational Modelling in Warsaw, Poland, under Grant no. GB77-11.
Funding
National Science Centre, Poland (NCN) under Grant no. 2015/17/D/ST4/00112.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
None.
Availability of data and material (data transparency)
Upon request, stored in local repository.
Code availability (software application or custom code)
Free software was used: ORCA (https://orcaforum.kofo.mpg.de/app.php/portal), Multiwfn (http://sobereva.com/multiwfn/), VMD (https://www.ks.uiuc.edu/Research/vmd/).
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Published as part of the topical collection of articles from the 17th edition of the Central European Symposium on Theoretical Chemistry (CESTC 2019) in Austria.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kubas, A. Characterization of charge transfer excited states in [2Fe–2S] iron–sulfur clusters using conventional configuration interaction techniques. Theor Chem Acc 139, 120 (2020). https://doi.org/10.1007/s00214-020-02635-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00214-020-02635-7