1 Introduction

Calculations of nuclear spin–spin coupling constants, important structural parameters, present some unique challenges. Firstly, electron correlation plays a crucial role for these second-order response properties, since, at the nonrelativistic level, they are determined mostly by triplet perturbation operators, which means that the Hartree–Fock results, often affected by triplet instabilities, are practically meaningless [1]. Secondly, they are properties associated with electron density at the nucleus, where the electron velocity is the largest, which means that in heavy-element containing compounds relativistic effects are expected to play a large role. In fact, it turns out that the relativistic phenomena affect not only the NMR parameters of heavy nuclei, but also of the nearby light nuclei, the phenomenon known as heavy-atom-on-light-atom (HALA) effect (see e.g., Refs. [2, 3]).

Accurate description of the electron density at the nucleus, and therefore also the nuclear spin–spin coupling constants, requires also specially constructed basis sets with large number of ’tight’ functions. Another factor contributing to the difficulty of calculations of the spin–spin coupling constants is their strong dependence on molecular geometry, and, therefore, relatively large vibrational effects.

In contemporary computational quantum chemistry, there are two approaches to electron correlation: the use of density functional theory and of conventional methods, employing wave function models based on the Hartree–Fock approximation. Among the latter methods, the coupled-cluster (CC) theory is probably the most successful one. As far as the spin–spin coupling constants calculations are concerned, both approaches are proven to be useful. The coupled-cluster theory presents the advantage of taking the electron correlation into account in a systematic manner, allowing for hierarchical improvement of the results. On the other hand, the performance of DFT strongly depends on the analytical form of the exchange–correlation functional. However, DFT is often more efficient then CC in terms of resource/performance ratio, and, moreover, it is currently the only correlated computational method implemented for calculations of molecular properties such as spin–spin coupling constants with relativistic Hamiltonians. More information about these theoretical methods and their application in the studies of spin–spin coupling constants can be found in numerous works (see e.g., [4,5,6,7]) and reviews (see e.g., [8,9,10] and references therein).

Over the years, there has been a number of both experimental [11,12,13,14,15,16] and computational [17,18,19,20] studies of the coupling constants in variously substituted acetylenes. Ref. [16] presents an extensive review of the experimentally measured coupling constants in these compounds. In Ref. [17], the values of \(^{1}J_{C{\equiv }C}\) for a large series of substituted acetylenes have been calculated using the DFT method. Not only did the DFT calculated data follow the trends observed for the experimental results, but also the values were in satisfactory agreement with the experiment (in most cases within several Hz). However, no relativistic effects were taken into account and the agreement was obviously worse for heavy atom-substituted acetylene derivatives. No vibrational corrections were taken into account, either. Apart from the commonly investigated values of \(^{1}J_{C{\equiv }C}\) also other coupling constants involving the alkynyl carbon atoms,\(^{1}J_{HC{\equiv }}\) and \(^{2}J_{H,C{\equiv }}\), were analyzed. In Ref. [14] the experimental values of carbon-tin and carbon-lead spin–spin coupling constants in alkynyl tin(IV) and alkynyl lead(IV) compounds have been presented, including \(^{1}J_{SnC{\equiv }}\), \(^{1}J_{PbC{\equiv }}\), \(^{2}J_{Sn,C{\equiv }}\) and \(^{2}J_{Pb,C{\equiv }}\). In the most recent work [20], relativistic effects on the shielding and spin–spin coupling constants in methyl-substituted acetylene derivatives were examined.

The aim of this work is to calculate spin–spin coupling constants in a series of acetylenes \(\hbox {HC}{\equiv }\hbox {CXH}_3\), including those containing heavy atoms (X is C, Si, Ge, Sn, Pb). Particular attention is paid to the vibrational corrections and comparison of the geometry derivatives calculated at the relativistic (with four-component Dirac–Coulomb Hamiltonian) and nonrelativistic level. We discuss the results for \(^{1}J_{C{\equiv }C}\), \(^{1}J_{HC{\equiv }}\), \(^{2}J_{H,C{\equiv }}\), \(^{1}J_{XC{\equiv }}\) and \(^{2}J_{X,C{\equiv }}\) constants, which have been observed in the experiment. Since the experimental data mostly come from the ethylene-substituted derivatives, nonrelativistic DFT calculations have been carried out also for these compounds (too bulky for coupled-cluster or relativistic four-component calculations) to assess the effect of the substitution.

2 Computational details

Nonrelativistic DFT calculations of nuclear spin–spin coupling constants used to study the influence of basis set and exchange–correlation functional choice have been performed with the Dalton program [21]. Three different exchange–correlation functionals: BLYP, B3LYP, BHLYP and two different basis sets have been used. In the first basis set, later referred to as basis set A, for all atoms the all-electron augmented triple-\(\zeta\) set with polarization functions (ATZP) [22,23,24] basis set has been used. For acetylene derivative containing lead ADZP basis set [25, 26] was used instead of ATZP. In the basis set B, we used for the light atoms (hydrogen, carbon) augmented version of triple-\(\zeta\) Dunning basis set modified for spin–spin coupling constants (aug-cc-pVTZ-J) [27] and ATZP (ADZP for lead-containing molecule) basis set for heavy atoms (silicon, germanium, tin, lead). All of these basis sets have been uncontracted. The nonrelativistic calculations have been carried out using point-nucleus model.

Furthermore, nonrelativistic DFT calculation of vibrationally averaged spin–spin coupling constants have been performed employing the B3LYP functional (we report only basis set A results; similar values have been obtained with basis set B). The method, relying on second-order perturbation theory and requiring the first and diagonal second derivatives of the spin–spin coupling constant as well as the harmonic frequencies and the semi-diagonal part of the cubic force field (described in detail in Ref. [28]), is implemented in the Dalton program.

The nonrelativistic CC calculations have been performed at the coupled-cluster singles-and-doubles (CCSD) level using the CFOUR program [29] (modified locally to include the g factors for the heavy nuclei). To optimize the CCSD molecular geometries, the basis set A in contracted form has been used. To compute the coupling constants the same basis sets, but in uncontracted form were applied.

The relativistic four-component DFT calculations of spin–spin coupling constants have been performed with Dirac program [30] using the default four-component Dirac–Coulomb Hamiltonian with the simple Coulombic correction [31]. The computations employed the B3LYP exchange–correlation functional and the uncontracted basis set B. These calculations have been carried out using Gaussian charge distribution nuclear model (some computations have also been performed using the point-nucleus model in order to compare the results). Additionally, corresponding nonrelativistic DFT calculations have been performed with Dirac program. These computations, used to assess the relativistic effects, have been carried out with the same computational parameters as the relativistic ones, with one exception: the value of the speed of light has been increased to 2000 a.u.

The geometric parameters of acetylene derivatives under study have been obtained through structure optimization; the relevant results are shown in the Appendix. Relativistic geometries are based on four-component DFT calculations (similar approach has recently been used in Ref. [32]). Unless otherwise noted, the following calculation of the nuclear spin–spin coupling constants has been carried out on the same level of theory as the structure optimization.

The derivatives of the coupling constants with respect to a single geometry parameter have been computed numerically using the three-point formula for the optimized geometry.

It should be noted that we did not want to use a different basis set at each stage (geometry optimization, geometry derivatives, relativistic contribution etc.), as it would make the comparison between the calculated values even harder and the aim of this work was to examine a simple methodology that could be used more routinely.

3 Results and discussion

We begin with the comparison of spin–spin coupling constants calculated for acetylene derivatives substituted either with ethylene groups or with hydrogen atoms so as to estimate the changes resulting from this substitution. Afterward, the influence of the chosen basis set and nucleus model will be studied. Then, the values of coupling constants obtained with CC method and nonrelativistic DFT method will be compared in order to evaluate the performance of different exchange–correlation functionals in reproducing the electron correlation. Next, a comparison between nonrelativistic and relativistic DFT values will be drawn so as to estimate the contribution of relativistic effects. Finally, the zero-point vibrational corrections to spin–spin coupling constants calculated at nonrelativistic DFT level of theory will be presented. The derivatives of the calculated coupling constants with respect to single geometry parameters (relativistic and nonrelativistic results) will be examined in order to assess the quality of vibrational corrections calculated at the nonrelativistic level.

The values of spin–spin coupling constants, J, will be given in Hz, the values of the reduced constants, K, in \(10^{-19} \hbox {J}\;\hbox {T}^{-2}\;\hbox {s}^{-1}\). The K values will be used whenever we compare the coupling constants for different X nuclei.

3.1 The influence of the substitution of H atoms with ethylene groups

Most of the available experimental data refer to ethylene-substituted acetylene derivatives \(\hbox {HC}{\equiv }\hbox {CX}(\hbox {C}_2\hbox {H}_5)_3\), whereas the coupling constants discussed below in detail have been calculated for compounds containing hydrogen atoms instead of ethylene groups. Therefore, the influence of the substitution of H atoms with ethylene groups on the coupling constants was studied by comparing the nonrelativistic DFT values for both types of molecules. The results can be seen in Table 1.

Table 1 \(^{1}J_{C{\equiv }C}\), \(^{1}J_{HC{\equiv }}\), \(^{2}J_{H,C{\equiv }}\), \(^{1}J_{XC{\equiv }}\) and \(^{2}J_{X,C{\equiv }}\) values (in Hz) calculated for \(\hbox {HC}{\equiv }\hbox {CXH}_3\) and \(\hbox {HC}{\equiv }\hbox {CX}(\hbox {C}_{2}\hbox {H}_5)_3\) acetylene derivatives (nonrelativistic DFT approach, B3LYP functional, basis set B)
Full size table

The differences between coupling constants calculated for the studied acetylene derivatives and corresponding ethylene-substituted derivatives turn out to be significant, which makes it difficult to compare directly the computed values with the experimental ones. However, for the couplings not including a heavy atom, there are some trends that can be observed. The difference between the values obtained for \(\hbox {HC}{\equiv }\hbox {CXH}_3\) and \(\hbox {HC}{\equiv }\hbox {CX(C}_2\hbox {H}_5)_3\) fluctuates around 10 Hz in case of \(^{1}J_{C{\equiv }C}\), 5 Hz in case of \(^{1}J_{HC{\equiv }}\) and 2 Hz in case of \(^{2}J_{H,C{\equiv }}\). We note that although a different approach has been used in the recent study of \(\hbox {HC}{\equiv }\hbox {CX(CH}_3)_3\) acetylene derivatives [20] the values of the computed constants (except for Sn-compound) are in between our results for \(\hbox {HC}{\equiv }\hbox {CXH}_3\) and \(\hbox {HC}{\equiv }\hbox {CX(C}_2\hbox {H}_5)_3\) derivatives.

In order to make the comparison between the calculated values and the experimental ones easier, the evaluated ’experimental’ values for \(\hbox {HC}{\equiv }\hbox {CXH}_3\) will be given in parentheses next to the experimental values for \(\hbox {HC}{\equiv }\hbox {CX(C}_2\hbox {H}_5)_3\).

3.2 The basis set choice

In order to investigate the basis set dependence of the calculated spin–spin coupling constants, calculations have been carried out using basis sets A and B described in Sect. 2. The values of \(^{1}J_{C{\equiv }C}\), \(^{1}J_{HC{\equiv }}\) and \(^{1}J_{XC{\equiv }}\) obtained using different basis sets and B3LYP (see Table 2), BLYP and BHLYP functionals have been compared. In every case the absolute values obtained using basis set B were higher. What is more, the relative differences arising from the use of either basis set B or basis set A seem to be systematic (excluding \(\hbox {HC}{\equiv }\hbox {CPbH}_3\); however, in this case it is impossible to get reliable results employing a nonrelativistic method). No matter which exchange–correlation functional has been used, the relative difference between the values obtained with basis set B or basis set A comes to 6.3–6.7% for \(^{1}J_{C{\equiv }C}\), 3.6–4% for \(^{1}J_{XC{\equiv }}\) and 12.9–13% for \(^{1}J_{HC{\equiv }}\). In case of \(^{1}J_{HC{\equiv }}\) the experimental results (see Table 6 below) are in between the results obtained using basis sets A and B, with the basis set A values being somewhat closer to the experiment.

Table 2 \(^{1}J_{C{\equiv }C}\), \(^{1}J_{XC{\equiv }}\), \(^{1}J_{HC{\equiv }}\) values (in Hz) calculated using basis sets A (ATZP(ADZP)) and B (aug-cc-pVTZ-J \(+\) ATZP(ADZP)) (nonrelativistic DFT approach, B3LYP functional)
Full size table

In principle, stand-alone aug-cc-pVTZ-J basis set should give better results in spin–spin coupling calculations, since it was specially modified for this use. It contains tight exponents necessary for a proper description of the electron density close to the nuclei, probed in the NMR experiment. On the other hand, in case of this work the performance of ATZP basis set seems to be more satisfying, since the obtained values are in better agreement with the experiment. There is a possibility that for the ATZP basis set different effects have canceled out, thus giving results closer to the experimental values.

3.3 Electron correlation effects

First, the values of the constants obtained with CC method and nonrelativistic DFT method using different exchange–correlation functionals: BLYP, B3LYP and BHLYP have been compared. All the results are collected in Tables 3 and 4 together with the experimental data. Each set of calculations has been carried out within the same approach as used for geometry optimization, with the exception of CC calculation for the tin compound. In this case, the bond lengths obtained using CC were unphysically small, and DFT-optimized geometry has been used instead.

Table 3 \(^{1}J_{C{\equiv }C}\), \(^{1}J_{HC{\equiv }}\) and \(^{2}J_{H,C{\equiv }}\) values (in Hz) calculated using CC method (basis set A) and DFT method (basis set A) with BLYP, B3LYP and BHLYP functionals
Full size table
Table 4 \(^{1}J_{XC{\equiv }}\) and \(^{2}J_{X,C{\equiv }}\) values (in Hz) calculated using CC method (basis set A) and DFT method (basis set A) with BLYP, B3LYP and BHLYP functionals
Full size table

A priori, the CC method should, at least as long as heavy atoms are not present and relativistic effects are negligible, give results in better agreement with experiment than DFT. The values of \(^{1}J_{C{\equiv }C}\) obtained by the CC method are indeed in much better agreement with the experiment than these obtained with any of the used DFT functionals. However, DFT values of \(^{1}J_{HC{\equiv }}\) are closer to the experiment than those obtained by the CC method. It is possible that in this case the environmental effects, neglected in the calculations, counterbalance the deficiencies of the DFT method.

One of the aims of this work was to assess the performance of different exchange–correlation functionals. For the \(^{1}J_{C{\equiv }C}\) constants, the BLYP functional gave results that were in the best agreement both with the values obtained by the CC method and with the experiment. The B3LYP values vary only slightly (up to 4%) from those calculated using the BLYP functional, whereas the differences between the values calculated using the BHLYP functional and the BLYP functional are bigger and reach almost 15%. For \(^{1}J_{XC{\equiv }}\) and \(^{2}J_{X,C{\equiv }}\) the B3LYP values were the closest to the CC results (there are not enough experimental data for comparison). In case of \(^{1}J_{HC{\equiv }}\), the BHLYP values are in best agreement with experiment, yet, the values computed using the B3LYP functional are the closest to the CC results. The \(^{2}J_{H,C{\equiv }}\) coupling constants obtained with the B3LYP and BHLYP functionals do not differ much (about 4%) and are in good agreement both with the experiment and with the CC values. Taking everything into consideration, the performance of the B3LYP functional seems to be the most satisfactory and consequently it was used in relativistic DFT calculations.

3.4 The model of the nucleus

Another factor which should be taken into account in relativistic calculations is the nucleus model [36]. We present the results obtained using the Gaussian charge distribution model. We have compared them with the values computed using the point-nucleus model, applying the relativistic DFT approach, B3LYP functional and basis set B. We do not show these values, since in most cases the difference between point-nucleus and finite-nucleus model is below 0.2 Hz, the only exceptions are \(^{1}J_{XC{\equiv }}\) and \(^{2}J_{X,C{\equiv }}\) couplings in \(\hbox {HC}{\equiv }\hbox {CSnH}_3\) and \(\hbox {HC}{\equiv }\hbox {CPbH}_3\). When the change from point-nucleus to finite-nucleus model is made, a reduction by about 0.2% of the total value for \(\hbox {HC}{\equiv }\hbox {CSnH}_3\) and 2% for \(\hbox {HC}{\equiv }\hbox {CPbH}_3\) in the results can be noticed.

3.5 Relativistic effects

Unfortunately, at present, there is no possibility to include the relativistic effects in the CC calculations of the spin–spin coupling constants; in most cases, relativistic DFT approach is applied to take electron correlation into account (see e.g., Refs. [37,38,39] and references therein). All relativistic computations in this work have been performed using the four-component DFT method.

To investigate the relativistic effects, the values obtained using the Dirac program with relativistic and nonrelativistic approach were compared. In case of the couplings that do not involve a heavy atom (\(^{1}J_{C{\equiv }C}\), \(^{1}J_{HC{\equiv }}\), \(^{2}J_{H,C{\equiv }}\)), the differences between nonrelativistic and relativistic results are negligible. The largest differences occur for \(\hbox {HC}{\equiv }\hbox {CPbH}_3\), but even in this case they do not exceed 1.5% of the total value (2 Hz for \(^{1}J_{C{\equiv }C}\), 2.7 Hz for \(^{1}J_{HC{\equiv }}\), 0.7 Hz for \(^{2}J_{H,C{\equiv }}\)).

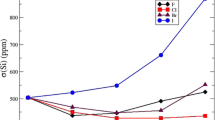
As shown in Table 5, the relativistic effects on the couplings that involve a heavy atom (\(^{1}J_{XC{\equiv }}\), \(^{2}J_{X,C{\equiv }}\)) become relevant for the molecules that contain tin and lead. For \(\hbox {HC}{\equiv }\hbox {CSiH}_3\) and \(\hbox {HC}{\equiv }\hbox {CGeH}_3\) the constants calculated with relativistic and nonrelativistic approach differ by only about 1.5% of the total value in case of \(^{1}J_{XC{\equiv }}\) and about 2.5% in case of \(^{2}J_{X,C{\equiv }}\), whereas the difference between the relativistic and nonrelativistic results for \(^{1}J_{XC{\equiv }}\) for \(\hbox {HC}{\equiv }\hbox {CSnH}_3\) and \(\hbox {HC}{\equiv }\hbox {CPbH}_3\) is significant, since it is 30.8 Hz (over 5% of the total value) for the tin-containing molecule and 198.8 Hz (almost 50% of the total value) for the lead-containing molecule. The comparison of relativistic and nonrelativistic results for \(^{2}J_{X,C{\equiv }}\) for \(\hbox {HC}{\equiv }\hbox {CSnH}_3\) and \(\hbox {HC}{\equiv }\hbox {CPbH}_3\) indicates that, in this case, the relativistic effects are more pronounced in the tin-containing molecule. The difference in \(^{2}J_{X,C{\equiv }}\) for \(\hbox {HC}{\equiv }\hbox {CSnH}_3\) comes to 14 Hz, that is \(\approx 10\%\) of the total value, whereas for \(\hbox {HC}{\equiv }\hbox {CPbH}_3\) it is only 6.6 Hz, \(\approx 6\%\) of the total value.

Table 5 \(^{1}J_{XC{\equiv }}\) and \(^{2}J_{X,C{\equiv }}\) values (in Hz) calculated using relativistic and nonrelativistic approach (B3LYP functional, basis set B)
Full size table

All in all, it appears that in case of the discussed acetylene derivatives it is sufficient to consider the relativistic effects only for the \(^{1}J_{XC{\equiv }}\) and \(^{2}J_{X,C{\equiv }}\) coupling constants and for the tin- and lead-containing molecules. Essentially, the differences between the values calculated using the nonrelativistic and relativistic methods are significant only for these couplings.

3.6 Vibrational effects

Spin–spin coupling constants depend strongly on the nuclear positions, which means that they often have large vibrational contributions and exhibit a strong temperature dependence [8, 40]. Consequently, particularly the zero-point vibrational (ZPV) corrections cannot be neglected when a comparison with experimental data is made. For instance, in acetylene, the vibrational correction to \(^{1}J_{C{\equiv }C}\) exceeds 10 Hz [41].

The ZPV correction to a given property can be calculated from the expectation value of this property over the vibrational ground-state wave function, therefore calculating vibrational corrections to the coupling constants for polyatomic molecules is computationally demanding. Thus, it becomes cost-effective to calculate the equilibrium values of the coupling constants at an advanced level of theory, and then estimate the vibrational corrections at a less expensive level, for instance DFT [8]. We use here such a simplified approach, vibrationally averaging spin–spin coupling constants at the nonrelativistic DFT level and then comparing the dependence of the coupling constants on selected geometry parameters as calculated with nonrelativistic and relativistic Hamiltonians.

3.6.1 Nonrelativistic ZPV corrections

The comparison of vibrationally averaged spin–spin coupling constants and the results for the optimized geometry can be found in Tables 6 and 7.

Table 6 Optimized geometry values of \(^{1}J_{C{\equiv }C}\), \(^{1}J_{HC{\equiv }}\) and \(^{2}J_{H,C{\equiv }}\) constants, vibrationally averaged values (nonrelativistic DFT, basis set A, B3LYP functional) and estimated experimental data (in Hz)
Full size table
Table 7 Optimized geometry values of \(^{1}K_{XC{\equiv }}\) and \(^{2}K_{X,C{\equiv }}\), vibrationally averaged values (nonrelativistic DFT, basis set A, B3LYP functional) and the experimental data
Full size table

For \(^{1}J_{C{\equiv }C}\), \(^{1}J_{HC{\equiv }}\), \(^{2}J_{H,C{\equiv }}\) the ZPV correction does not change significantly with the X atom, whereas for the values of reduced spin–spin coupling constants of carbon and the X atom (\(^{1}K_{XC{\equiv }}\), \(^{2}K_{X,C{\equiv }}\)) a clear trend can be observed. With the increase in the atomic number of the X atom, the value of the ZPV correction increases.

In most cases (\(^{1}J_{C{\equiv }C}\), \(^{2}J_{H,C{\equiv }}\), \(^{1}J_{HC{\equiv }}\), \(^{1}J_{XC{\equiv }}\)) the differences between the vibrationally averaged and optimized geometry results constitute only 2–4% of the values. For \(^{1}J_{C{\equiv }C}\) and \(^{1}J_{HC{\equiv }}\) the addition of the ZPV correction leads to improved agreement with the experimental values. As far as \(^{2}J_{X,C{\equiv }}\) is concerned, the difference exceeds 10% of the value.

3.6.2 Comparison of vibrational effects computed with relativistic and nonrelativistic method

In order to estimate the importance of different vibrational effects, the derivatives of the coupling constants with respect to the \(\hbox {C}{\equiv }\hbox {C}\) and \(\hbox {C}{-}\hbox {X}\) bond length have been computed, both with relativistic and nonrelativistic method. In addition, second derivatives of the constants with respect to \(\hbox {C}{\equiv }\hbox {C}-\hbox {X}\) angle have been calculated (the first derivatives vanish by symmetry). All the results can be found in Table 8. To interpret the role of the relativistic effects, we have also computed the derivatives with respect to the \(\hbox {C}{\equiv }\hbox {C}\) bond length at the relativistic equilibrium geometry, but using the nonrelativistic approach.

Table 8 Derivatives of reduced coupling constants with respect to the \(\hbox {C}{\equiv }\hbox {C}\) and the \(\hbox {C}{-}\hbox {X}\) bond length and second derivatives with respect to the \(\hbox {C}{\equiv }\hbox {C}{-}\hbox {X}\) angle computed with relativistic and nonrelativistic method (B3LYP functional, basis set B)
Full size table

The conclusions that can be drawn from the comparison of the nonrelativistic and relativistic values of derivatives of the coupling constants with respect to the bond lengths and of the second derivatives with respect to the angle are largely similar to the conclusions drawn from the comparison of the corresponding coupling constants. In case of the couplings that do not include a heavy atom (\(^{1}J_{C{\equiv }C}\), \(^{1}J_{HC{\equiv }}\), \(^{2}J_{H,C{\equiv }}\)) the differences between nonrelativistic and relativistic results are small, whereas larger differences occur for the couplings that include a heavy atom (\(^{1}J_{XC{\equiv }}\), \(^{2}J_{X,C{\equiv }}\)). On the other hand, in case of the coupling constants the relativistic effects became observable only for tin- and lead-containing molecules, whereas for the first and second derivatives of the coupling constants these effects can be clearly seen also for the germanium-containing molecule. As far as the derivative of \(^{1}J_{XC{\equiv }}\) with respect to the \(\hbox {C}{\equiv }\hbox {C}\) bond length is concerned, with the change from nonrelativistic to relativistic approach for the lead-containing molecule the absolute value increases by one order of magnitude. A sign change can also be observed for the second derivative of \(^{2}J_{X,C{\equiv }}\) with respect to the \(\hbox {C}{\equiv }\hbox {C}{-}\hbox {X}\) angle in case of lead-containing molecule. This indicates, not unexpectedly, that the derivatives of the coupling constants with respect to geometric parameters are even more sensitive to the relativistic effects than the coupling constants.

All the discussed reduced coupling constants are positive. When the first derivatives of the reduced spin–spin coupling constants (\(K'\) values) are analyzed a clear trend can be noticed. For each of the derivatives under consideration: \(^{1}K'_{C{\equiv }C}\), \(^{1}K'_{HC{\equiv }}\), \(^{2}K'_{H,C{\equiv }}\), \(^{1}K'_{XC{\equiv }}\) and \(^{2}K'_{X,C{\equiv }}\) the value of the derivative decreased with the increase in the atomic number of the X atom. There were only two significant exceptions - the nonrelativistic values of \(^{1}K'_{HC{\equiv }}\) and \(^{1}K'_{XC{\equiv }}\) for the tin-containing molecule. A comparison with the nonrelativistic derivatives with respect to the \(\hbox {C}{\equiv }\hbox {C}\) bond length computed at the relativistic equilibrium geometry indicates that in this case the latter values are correct (in all the other cases, the nonrelativistic \(K'\) values computed at nonrelativistic and relativistic equilibrium geometries were similar—e.g., the largest difference for Ge-containing molecule was \(\approx 15\%\)).

The same trend can be observed for the second derivatives (\(K''\) values) with respect to the \(\hbox {C}{\equiv }\hbox {C}{-}\hbox {X}\) angle, however, in this case the values for \(\hbox {HC}{\equiv }\hbox {CCH}_3\) stand out.

In Ref. [41] SOPPA(CCSD) calculated coordinate and internal valence coordinate coefficients for each of the four spin–spin coupling surfaces of the acetylene molecule—\(^{1}J(C,H)\), \(^{1}J(C,C)\), \(^{2}J(C,H)\), and \(^{3}J(H,H)\)—have been presented. It has been shown that for acetylene the dominant nuclear motion effect comes from bending at the carbon atoms, with stretching being of greater importance only for \(^{1}J(C,H)\). The comparison of some of the values calculated for \(\hbox {HC}{\equiv }\hbox {CCH}_3\) with those for acetylene (Table 8) suggests that the role of the nuclear motion effects on the spin–spin coupling constants for \(\hbox {HC}{\equiv }\hbox {CXH}_3\) might be similar.

It should be noted at this point that since the relativistic effects on the derivatives of the coupling constants with respect to molecular geometry parameters tend to be more pronounced than on the coupling constants themselves, the zero-point vibrational corrections calculated at the nonrelativistic level are not necessarily reliable. The relativistic effects on the quadratic and cubic force field (not investigated in this work) may also contribute.

4 Summary and conclusions

The nuclear spin–spin coupling constants calculated for a series of acetylene derivatives \(\hbox {HC}{\equiv }\hbox {CXH}_3\), where X is an element from group XIV of the periodic table (C, Si, Ge, Sn, Pb), have been presented. The calculations have been performed using different methods (nonrelativistic CC, nonrelativistic and relativistic DFT) in order to estimate the effects of electron correlation and relativity.

The values of coupling constants obtained with CC method and nonrelativistic DFT method have been compared in order to investigate the performance of DFT in the description of electron correlation. The CC method reproduced the experimental values better in case of \(^{1}J_{C{\equiv }C}\), however, in case of \(^{1}J_{HC{\equiv }}\) and \(^{2}J_{H,C{\equiv }}\) the DFT method brought the results in better agreement with the experiment. As far as the performance of different exchange–correlation functionals in reproducing the electron correlation is concerned, the use of B3LYP functional turns out to be the most satisfactory. The BLYP values vary only slightly (up to 4%) from those calculated using the B3LYP functional, whereas the differences between the values calculated using the BHLYP functional and the B3LYP functional are bigger and come to almost 15%.

For the studied systems, the use of ATZP basis set gives results in better agreement with the experiment than the aug-cc-pVTZ-J basis set. No matter which exchange–correlation potential has been used, the relative difference between the values obtained with basis set B or basis set A comes to approximately 7% for \(^{1}J_{C{\equiv }C}\), 4% for \(^{1}J_{HC{\equiv }}\) and 13% for \(^{1}J_{XC{\equiv }}\).

A comparison between nonrelativistic and relativistic DFT results has been drawn to estimate the contribution of relativistic effects. In case of the molecules under consideration it is sufficient to take the relativistic effects into account only for the couplings including heavy atoms (\(^{1}J_{XC{\equiv }}\) and \(^{2}J_{X,C{\equiv }}\) for the tin- and lead-containing molecules), in these cases the difference between the relativistic and nonrelativistic value can reach almost 50% of the value. In general, as far as the acetylene derivatives including a light X atom are concerned, proper description of the electron correlation seems to have greater impact on the calculated values of the coupling constants than the relativistic effects. Furthermore, the difference between point-nucleus and finite-nucleus model is negligible.

The calculations of the derivatives of the coupling constants confirm that in the comparison with experiment the related vibrational effects should be taken into account. It appears that, similarly to acetylene, the \({C{\equiv }C{-}X}\) bending motion might be the most significant. Moreover, the derivatives of the coupling constants are even more sensitive to the relativistic effects than the corresponding constants.

One factor which we did not take into account are solvent effects. As a rule, they do not affect significantly the nuclear spin–spin coupling constants, however, \(^{1}J_{\mathrm{CC}}\) in acetylene has been shown to be an exception [42]. The coupling constants transmitted through triple bonds in the studied acetylene derivatives may change to similar extent (5–6%).