Quantum dynamics of a plasmonic metamolecule with a time-dependent driving

Abstract

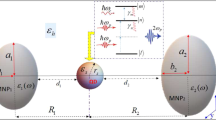
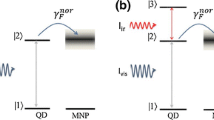
We simulate the dynamics of a quantum dot coupled to the single resonating mode of a metal nanoparticle. Systems like this are known as metamolecules. In this study, we consider a time-dependent driving field acting onto the metamolecule. We use the Heisenberg equations of motion for the entire system, while representing the resonating mode in Wigner phase space. A time-dependent basis is adopted for the quantum dot. We integrate the dynamics of the metamolecule for a range of coupling strengths between the quantum dot and the driving field, while restricting the coupling between the quantum dot and the resonant mode to weak values. By monitoring the average of the time variation in the energy of the metamolecule model, as well as the coherence and the population difference in the quantum dot, we observe distinct nonlinear behavior in the case of strong coupling to the driving field.

Appendices

Appendix 1: Adimensional coordinates and parameters

Upon indicating the dimensional coordinates and parameters with a prime, and introducing the energy scale $\hbar \omega _{{\mathrm{a}}}'$, we have the following definitions:

$$\begin{aligned} \varOmega= & {} \frac{\varOmega '}{\omega _{{\mathrm{a}}}'} , \end{aligned}$$

(28)

$$\begin{aligned} P= & {} \frac{P'}{\sqrt{M'\hbar \omega _{{\mathrm{a}}}'} }, \end{aligned}$$

(29)

$$\begin{aligned} R= & {} \sqrt{\frac{\hbar \omega _{{\mathrm{a}}}'}{\hbar }} R', \end{aligned}$$

(30)

$$\begin{aligned} \omega= & {} \frac{\omega '}{\omega _{{\mathrm{a}}}'},\end{aligned}$$

(31)

$$\begin{aligned} c= & {} \frac{c'}{\sqrt{ \hbar \omega _{{\mathrm{a}}}^{\prime 3}M'}},\end{aligned}$$

(32)

$$\begin{aligned} g= & {} \frac{g'}{\hbar \omega _{{\mathrm{a}}}'},\end{aligned}$$

(33)

$$\begin{aligned} \beta&= {} \hbar \omega _{{\mathrm{a}}}'\beta '\;. \end{aligned}$$

(34)

The symbol M is the inertial parameter of the oscillator, which has been set to unity. Upon choosing $\omega _{{\mathrm{a}}}'$ in such a way that the frequency $\omega =0.5$ of the oscillator in Eq. (16) corresponds to the value $\omega '=8.9 \times 10^{12}$ Hz, which is typical for the dynamics of metal nanoparticles [14], we obtain a spanned timescale in our simulations of $5.62 \times 10^{-12}$ s and an energy variation for the quantum dot, as shown in Fig. 4, of 24.6 meV.

Appendix 2: Phase-space-grid algorithm

The equation of the density matrix in the partial Wigner representation is analogous to that given in Eq. (4):

$$\begin{aligned} \frac{\partial }{\partial t}\hat{\rho }(X,t)=-\frac{i}{\hbar }\left[ \begin{array}{cc} \hat{H}_{{\mathrm{W}}}(X)&\hat{\rho }_{{\mathrm{W}}}(X,t)\end{array}\right] {{\mathcal {D}}} \left[ \begin{array}{c}\hat{H}_{{\mathrm{W}}}(X) \\ \hat{\rho }_{{\mathrm{W}}}(X,t)\end{array}\right] \;. \end{aligned}$$

(35)

Using the basis defined by $\hat{H}_{{\mathrm{S}}}|\alpha \rangle = \epsilon _{\alpha } |\alpha \rangle$ ($\alpha =1,2$), Eq. (35) can be written as

$$\begin{aligned} \frac{\partial }{\partial t}\rho _{{\mathrm{W}}}^{\alpha \alpha '}(R,P,t)= & {} -i\tilde{\omega }_{\alpha \alpha '}\rho _{{\mathrm{W}}}^{\alpha \alpha '}-L\rho _{{\mathrm{W}}}^{\alpha \alpha '}- \frac{i}{\hbar }\left( H_{{\mathrm{C,W}}}^{\alpha \beta }\rho _{{\mathrm{W}}}^{\beta \alpha '} - \rho _{{\mathrm{W}}}^{\alpha \beta '}H_{{\mathrm{C,W}}}^{\beta '\alpha '}\right) \nonumber \\&- \frac{i}{\hbar }\left( H_{E}^{\alpha \beta }\rho _{{\mathrm{W}}}^{\beta \alpha '} - \rho _{{\mathrm{W}}}^{\alpha \beta '}H_{E}^{\beta '\alpha '}\right) \nonumber \\&+ \frac{1}{2}\left( \frac{\partial H_{{\mathrm{C,W}}}^{\alpha \beta }}{\partial R}\frac{\partial \rho _{{\mathrm{W}}}^{\beta \alpha '}}{\partial P} + \frac{\partial \rho _{{\mathrm{W}}}^{\alpha \beta '}}{\partial P}\frac{\partial H_{{\mathrm{C,W}}}^{\beta '\alpha '}}{\partial R}\right), \end{aligned}$$

(36)

where the frequency $\tilde{\omega }_{\alpha \alpha '} = \left( \epsilon _{\alpha } - \epsilon _{\alpha '}\right) /\hbar$ has been defined. The Liouville operator, L, is given by

$$\begin{aligned} L = P\frac{\partial }{\partial R}- \frac{\partial H_{B,W}}{\partial R}\frac{\partial }{\partial P}\;. \end{aligned}$$

(37)

One can introduce the following frequencies $\tilde{\omega }^{\alpha \alpha '}$:

$$\begin{aligned}&\tilde{\omega }^{11} = 0, \quad \tilde{\omega }^{22} = 0, \nonumber \\&\tilde{\omega }^{12} = \varOmega , \quad \tilde{\omega }^{21} = -\hbar \varOmega . \end{aligned}$$

(38)

The equations of motion for matrix elements of the density operator can be written explicitly as:

$$\begin{aligned} \frac{\partial }{\partial t}\rho _{{\mathrm{W}}}^{11}(R,P,t)= & {} \frac{i}{\hbar }cR\left( 2i\text {Im}\left[ \rho _{{\mathrm{W}}}^{21}\right] \right) -\frac{i}{\hbar }g\cos (\omega _{d}t)\left( 2i\text {Im}\left[ \rho _{{\mathrm{W}}}^{21}\right] \right) \nonumber \\&- L\rho _{{\mathrm{W}}}^{11}- \frac{c}{2}\frac{\partial }{\partial P}\left( 2\text {Re}\left[ \rho _{{\mathrm{W}}}^{21}\right] \right), \end{aligned}$$

(39)

$$\begin{aligned} \frac{\partial }{\partial t}\rho _{{\mathrm{W}}}^{21}(R,P,t)= & {} {-}i\tilde{\omega }_{21}\rho _{{\mathrm{W}}}^{21}+ \frac{i}{\hbar }cR\left( \rho _{{\mathrm{W}}}^{11} - \rho _{{\mathrm{W}}}^{22}\right) -\frac{i}{\hbar }g\cos (\omega _{d}t)\left( \rho _{{\mathrm{W}}}^{11}- \rho _{{\mathrm{W}}}^{22}\right) \nonumber \\&- L\rho _{{\mathrm{W}}}^{21}- \frac{c}{2}\frac{\partial }{\partial P}\left( \rho _{{\mathrm{W}}}^{11}+\rho _{{\mathrm{W}}}^{22}\right), \end{aligned}$$

(40)

$$\begin{aligned} \frac{\partial }{\partial t}\rho _{{\mathrm{W}}}^{22}(R,P,t)= & {} -\frac{i}{\hbar }cR\left( 2i\text {Im}\left[ \rho _{{\mathrm{W}}}^{21}\right] \right) +\frac{i}{\hbar }g\cos (\omega _{d}t)\left( 2i\text {Im}\left[ \rho _{{\mathrm{W}}}^{21}\right] \right) \nonumber \\&- L\rho _{{\mathrm{W}}}^{22}- \frac{c}{2}\frac{\partial }{\partial P}\left( 2\text {Re}\left[ \rho _{{\mathrm{W}}}^{21}\right] \right) \,. \end{aligned}$$

(41)

In order to simplify the integration, one can use the definition

$$\begin{aligned} \rho _{{\mathrm{W}}}^{\alpha \alpha '}(X,t)=\eta _{{\mathrm{W}}}^{\alpha \alpha '}(X,t) e^{-i\tilde{\omega }^{\alpha \alpha '}t}\;. \end{aligned}$$

(42)

Hence, using dimensionless coordinates, the equations of motion become

$$\begin{aligned} \frac{\partial }{\partial t}\eta _{{\mathrm{W}}}^{11}= & {} -2cR\left( -\text {Re}\left[ \eta _{{\mathrm{W}}}^{21}\right] \sin \left( \tilde{\omega }_{21}t\right) + \text {Im}\left[ \eta _{{\mathrm{W}}}^{21}\right] \cos \left( \tilde{\omega }_{21}t\right) \right) \nonumber \\&+ 2g\cos {(\omega t)}\left( -\text {Re}\left[ \eta _{{\mathrm{W}}}^{21}\right] \sin \left( \tilde{\omega }_{21}t\right) + \text {Im}\left[ \eta _{{\mathrm{W}}}^{21}\right] \cos \left( \tilde{\omega }_{21}t\right) \right) \nonumber \\&- L\eta _{{\mathrm{W}}}^{11}- c\frac{\partial }{\partial P}\left( \text {Re}\left[ \eta _{{\mathrm{W}}}^{21}\right] \cos \left( \tilde{\omega }_{21}t\right) + \text {Im}\left[ \eta _{{\mathrm{W}}}^{21}\right] \sin \left( \tilde{\omega }_{21}t\right) \right), \end{aligned}$$

(43)

$$\begin{aligned} \frac{\partial }{\partial t}\eta _{{\mathrm{W}}}^{22}=\; & {} 2cR\left( -\text {Re}\left[ \eta _{{\mathrm{W}}}^{21}\right] \sin \left( \tilde{\omega }_{21}t\right) + \text {Im}\left[ \eta _{{\mathrm{W}}}^{21}\right] \cos \left( \tilde{\omega }_{21}t\right) \right) \nonumber \\&- 2g\cos {(\omega t)}\left( -\text {Re}\left[ \eta _{{\mathrm{W}}}^{21}\right] \sin \left( \tilde{\omega }_{21}t\right) + \text {Im}\left[ \eta _{{\mathrm{W}}}^{21}\right] \cos \left( \tilde{\omega }_{21}t\right) \right) \nonumber \\&- L\eta _{{\mathrm{W}}}^{22}- c\frac{\partial }{\partial P}\left( \text {Re}\left[ \eta _{{\mathrm{W}}}^{21}\right] \cos \left( \tilde{\omega }_{21}t\right) + \text {Im}\left[ \eta _{{\mathrm{W}}}^{21}\right] \sin \left( \tilde{\omega }_{21}t\right) \right), \end{aligned}$$

(44)

$$\begin{aligned} \frac{\partial }{\partial t}\left( \text {Re}\left[ \eta _{{\mathrm{W}}}^{21}\right] \right)= & {} {-}cR\left( \eta _{{\mathrm{W}}}^{11}- \eta _{{\mathrm{W}}}^{22}\right) \sin (\tilde{\omega }_{21}t)+g\cos (\omega _{d}t)\left( \eta _{{\mathrm{W}}}^{11}- \eta _{{\mathrm{W}}}^{22}\right) \sin (\tilde{\omega }_{21}t) \nonumber \\&- L\left( \text {Re}\left[ \eta _{{\mathrm{W}}}^{21}\right] \right) - \frac{c}{2}\frac{\partial }{\partial P}\left( \eta _{{\mathrm{W}}}^{11}+ \eta _{{\mathrm{W}}}^{22}\right) \cos (\tilde{\omega }_{21}t), \end{aligned}$$

(45)

$$\begin{aligned} \frac{\partial }{\partial t}\left( \text {Im}\left[ \eta _{{\mathrm{W}}}^{21}\right] \right)= & {} cR\left( \eta _{{\mathrm{W}}}^{11}- \eta _{{\mathrm{W}}}^{22}\right) \cos (\tilde{\omega }_{21}t) -g\cos (\omega _{d}t)\left( \eta _{{\mathrm{W}}}^{11}- \eta _{{\mathrm{W}}}^{22}\right) \cos (\tilde{\omega }_{21}t) \nonumber \\&- L\left( \text {Im}\left[ \eta _{{\mathrm{W}}}^{21}\right] \right) - \frac{c}{2}\frac{\partial }{\partial P}\left( \eta _{{\mathrm{W}}}^{11}+ \eta _{{\mathrm{W}}}^{22}\right) \sin (\tilde{\omega }_{21}t)\;. \end{aligned}$$

(46)

Equations (43), (44), (45), and (46) describe a set of coupled partial differential equations (PDE’s) which can be solved to obtain the elements of the density matrix as functions of time. In order to solve these coupled PDEs, the numerical integration approach known as the method of lines can be employed. The method of lines transforms the PDEs into a set of ordinary differential equations (ODEs) by using finite difference approximations for all but one of the integration variables. In this case, the phase-space derivatives are approximated, while the time variable is left un-approximated. For the types of potentials studied in this work, a fourth-order finite difference approximation for the phase-space derivatives proves to be more than sufficient:

$$\begin{aligned} \frac{{\text {d}}f}{{\text {d}} X} = \left( \frac{f(X - 2{\text {d}}X) - 8f(X - {\text {d}}X) + 8f(X + {\text {d}}X) - f(X + 2{\text {d}}X)}{12{\text {d}}X}\right) \,. \end{aligned}$$

(47)

Once the conversion from PDEs to ODEs has been performed, a numerical integration method can be utilized. In this work, a Runge-Kutta 5 Cash–Karp method was found to be suitable for stable numerical results. In such an approach, the phase space of the system is essentially discretized into a numerical grid, upon which the coupled ODEs are solved.