The generic geometry of helices and their close-packed structures

Abstract

The formation of helices is an ubiquitous phenomenon for molecular structures whether they are biological, organic, or inorganic, in nature. Helical structures have geometrical constraints analogous to close-packing of three-dimensional crystal structures. For helical packing the geometrical constraints involve parameters such as the radius of the helical cylinder, the helical pitch angle, and the helical tube radius. In this communication, the geometrical constraints for single helix, double helix, and for double helices with minor and major grooves are calculated. The results are compared with values from the literature for helical polypeptide backbone structures, the α-, π-, 3₁₀-, and γ-helices. The α-helices are close to being optimally packed in the sense of efficient use of space, i.e. close-packed. They are also more densely packed than the other three types of helices. For double helices comparisons are made to the A, B, and Z forms of DNA. The helical geometry of the A form is nearly close-packed. The packing density for the B and Z forms of DNA are found to be approximately equal to each other.

1 Introduction

Helical structures are common in chain molecules such as proteins, RNA, and DNA, e.g., α-helices and the A, B and Z forms of DNA. In this paper, we consider the packing of idealized helices formed by a continuous tube with the purpose to calculate the constraints on such helices which arise from close-packing and space filling considerations; we consider single helical tubes, as well as sets of two identical helical tubes. It is found that the efficiency of the use of space depends on the helical pitch angle, and the optimum helical pitch angle is determined for single and for double helices. This geometrical packing problem is an interesting variant of Kepler’s problem of the densest possible sphere packing [1].

Mathematical aspects of single helices has been considered previously with the purpose to understand their topology. Single helices has been investigated by Maritan et al. [2], and Przybył and Pierański [3]. Maritan et al. [2] introduced the thickness of a tube in terms of a new quantity called global radius of curvature. This was used in a numerical simulation of packing with the surprising result that the resulting center line defines a helix with a specific shape. In a succeeding paper, Przybył and Pierański [3] gave an analytical argument, which included the consideration of self-contact points for single helices, and led to the determination of the same helix as in the study of Maritan et al. [2]. This helix geometry is the one we describe as being tightly packed in the classification suggested below. In search of tight conformations of ideal knots, Pierański [4] has studied the tightly packed double helix, which has a helical pitch angle of 45°. In the context of two basic structural motifs in biology, the α-helix and the B form of DNA, these tightly packed helices has been discussed by Stasiak and Maddocks [5].

The importance of entropy for helix formation was later discussed by Snir and Kamien [6]. In their paper, a polymer is also modeled as a thick tube, but now immersed in a solution of hard spheres, which have an entropy depending on the polymers use of available space. It was shown by an entropy argument, that when the spheres are relatively small, the optimal shape of the polymer is again a helix of the shape originally found by Maritan et al. [2]. The complete classification of the single helices has been discussed in the Kirchhoff frame by Chouaieb et al. [7], and the close-packing of many rods has been studied by Starostin [8]. The work of Starostin generalizes the densest hexagonal packing of many infinite straight cylinders by applying a collective helical twist. A review of tube models of proteins has been given by Banavar and Maritan [9], see also Banavar et al. [10].

It would be interesting to extend and incorporate such topological arguments to the protein folding question, see Sali et al. [11], Mirny and Shakhnovich [12], and Trovato et al. [13].

2 Single helix

For molecular helices one often see preferences for a specific handedness; the continuous models presented here can not discern between left and right chirality from packing considerations and this distinction is not included in the analysis. The basic structures of a single helix can then be described as being in one of the following configurations.

2.1 Open helices

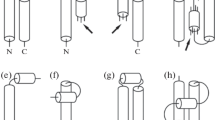
A single helical line has a sinuous trace through space on a cylindrical surface. The radius of this cylindrical surface is denoted a and referred to as the helical cylinder radius. The properties of a helix are uniquely defined by two geometrical quantities, e.g. curvature and torsion. Generally, the helix line will trace a relatively open structure, see Fig. 1a. The repetition length along the z-axis of the helix, also called the helix pitch, is denoted by H. It is convenient in the following to work with the reduced helix pitch, h = H/2π.

Fig. 1

Single helical tubes of finite diameter D. a Open helix on a cylinder of radius a; the repetition length is H = 2πh which then defines the slope of the curve. b Packed helix. In this case the distance from the center line to itself is equal to the diameter D of the tube. c Schematic representation of a tightly twisted helix; a is minimal (D is not shown to scale). d Tightly packed helix, in which case the center line helix has a critical h/a ratio. Depicted is the helix with a pitch angle of 21.8° and not 25.0° as the latter is prohibited by the generalized Poisson criterion

2.2 Packed helices

If one attempts to shorten the helix pitch, H, of an open helix while maintaining the radius, a, of the cylinder surface hosting the helical line, one will find that at a certain minimum helical pitch the distance from the helical line to itself becomes equal to the diameter, D, of the helical backbone tube. We call this geometry a packed helix, see Fig. 1b.

2.3 Tightly twisted helices

The helical line of a helix traces out a continuous path on the hosting cylinder. If the diameter of this cylinder is minimized while preventing the repetition length from diverging one obtains structures we will denote as being tightly twisted. The structure depicted in Fig. 1c is not tightly twisted; it would require a larger value of D, while maintaining H and a.

2.4 Tightly packed helices

If a helix is both packed and twisted we will use the notation that it is tightly packed, see Fig. 1d.

2.5 Generalized Poisson criterion

A note on the volume of the tubes: When studying three-dimensional deformations of bulk material it is sometimes useful to consider an ideal incompressible material, i.e. a material where the differential volume elements are preserved under shape changes. For solid materials these are the ones with a Poisson’s ratio of 0.5. For a helical tube, volume elements are not preserved: On the outer part of the helix the volume elements are expanded while on the inner part the volume elements are compressed. However, integrated these compressions and expansions cancel each other. Hence the backbone tube volume is differentially preserved along the helical line, of local curvature κ, as long as D ≤ 2/κ. We will call this a generalized Poisson criterion, and it will allow us to calculate absolute volumes in our analysis. Previously, in studies of helical topologies a criterion preventing the tube from bending into itself has been considered [2, 3, 14]. These two criteria are mathematically identical though their motivations can be phrased differently. When the generalized Poisson criterion is obeyed, the volume of a helical tube is πD ² L/4 where L is the curve-length of the helical line.

2.6 Differential geometry

We first review the geometry which is used in our analysis. A helix is a curve of constant curvature, κ, and torsion, τ, and can therefore be specified by two scalars [15]. It can equivalently well be specified by two alternative parameters, for example a and h, where a is the helix radius and H = 2πh the helix pitch (repetition length). For a single (infinite) helix, we have the parametric equation

$$ \mathbf{r}={\overrightarrow{OP}}= (a\cos t, a\sin t, ht) $$

(1)

for $t\in {\bf R}.$ The radius a and the reduced pitch h are related to the curvature and torsion as

$$ \kappa = {\frac{a}{a^2+h^2}}, \quad \tau= {\frac{h}{a^2+h^2}}. $$

(2)

The helix angle, v, is found through differentiation

$$ {\frac{{\rm d} \mathbf{r}}{{\rm d} t}} = (-a\sin t, a \cos t, h) $$

(3)

so that,

$$ \left|{\frac{{\rm d} \mathbf{r}} {{\rm d} t}}\right| = \sqrt{a^2+h^2}. $$

(4)

The tangent is therefore at an angle v (the helix angle) with respect to the vertical axis. This angle, v, and its complementary angle, or pitch angle, $v_{\bot} =90^{\circ} - v$ are determined by

$$ \cos v = \left( \left( {\frac{a}{h}} \right)^2 +1\right)^{-1/2}, \quad \cos v_\bot = \left( 1+ \left( {\frac{h}{a}} \right)^2 \right)^{-1/2}. $$

(5)

We will imagine that the helix above is the center line of a circular tube of radius D/2. This will give certain conditions on how such idealized tubes can be packed, which we describe in the following.

We now investigate self-contacts; for two points on the helical line to be in contact (on the surface of the tube) it is a requirement that their distance is a local minimum. Without loss of generality take two points on a helix with coordinates ${\mathbf{r}}_1=(a,0,0),$ and ${\mathbf{r}}_2=(a\cos t, a\sin t, ht).$ The square of their distance is

$$ D_{1}^2= |\overrightarrow{r_1r_2}|^2 = a^2(1-\cos t)^2 + a^2\sin^2 t + h^2t^2 $$

(6)

and the derivative hereof is

$$ {\frac{{\rm d}}{{\rm d}t}}|\overrightarrow{r_1r_2}|^2 = 2a^2\sin t+ 2h^2t. $$

(7)

Therefore, the local minima, which define possible self-contact points, are among the solutions to,

$$ \sin t+ {\frac{h^2}{a^2}}t=0 . $$

(8)

The solutions of this transient equation can be found numerically; in Fig. 2 the solutions are depicted in a $(t,v_{\bot})$ plot. It can be seen that for $v_\bot$ greater than a maximal value v _m , which is about 25.0°, the equation has no nontrivial solutions. This means that for these values, $v_{\bot} > v_m,$ no packed helical structures exist, but open helices, Fig. 1a, and twisted helices, Fig. 1c, are possible.

Fig. 2

Solutions $(t,v_{\bot})$ of the transient equation (8) for a single helix. The solutions are symmetric under t → −t; the vertical line in the middle corresponds to the trivial solution. The branch $t\in [-2\pi, -3\pi/2]$ represents solutions where a single helix can be packed. The maximal value of $v_{\bot}$ of the hairpin is 25.0°

Packed helical structures, Fig. 1b, are possible for $v_{\bot} < v_m,$ and arise when the tube diameter D is equal to D ₁ (the distance to the nearest self-contact point correspond to the branch of solutions $t \in [-2\pi, -{\frac{3\pi}{2}} ]).$ In Fig. 3 is shown the minimum values of 2a/D as a function of $v_{\bot}$ (see solid line). The structures on this line are packed. Also shown in Fig. 3 are the minimum values of 2a/D for which the generalized Poisson criterion is obeyed (see dashed line). Interestingly, as can be seen in the figure, structures with $v_\bot$ between v _p (21.8°) and v _m (25.0°) are prohibited by the generalized Poisson criterion from being packed. Hence, the structure at $v_\bot = v_p$ is both packed (limited by self-interactions) and tightly twisted (limited by minimization of a), i.e. a tightly packed helix, see Fig. 1d. This is the helix found in Refs. [2, 3].

Fig. 3

Single helix. Minimum values of 2a/D plotted as function of pitch angle $v_\bot$ (solid curve) which describes the packed helical structures. The minimum values of 2a/D which obey the generalized Poisson criterion are shown as the dashed curve. The crossing point is at $v_\bot = 21.8^{\circ}$

2.7 Close-packed helices

We now consider the efficiency of the use of volume for different helical structures. When selecting the most densely packed geometry one needs to compare with a reference volume. For this purpose we will here choose to consider an enclosing cylinder with volume V _E  = 2π² h(a + D/2)² and compare it to the volume, V _H , occupied by the helical tube, π² h D ²/(2 cosv). The packing efficiency is then calculated as the fraction of the volume occupied,

$$ f_V = V_H/V_E. $$

(9)

In Fig. 4 is shown f _V for the packed helices. The maximum is at $v_\bot^* = 18.1^{\circ},$ and the corresponding fraction of volume occupied is f ^* _V  = 0.784. It is interesting to notice that $v_\bot^* < 21.8^{\circ}:$ This means that for an efficient use of volume it is better to allow for a small central channel in the helix than to form a tightly packed helix. For the optimum close-packed single helix the channel radius is about 2.5% of a; e.g. if a = 2.5 Å then the channel width is only 0.1 Å.

Fig. 4

Volume fraction f _V for the packed helices (solid curve), and for twisted helices that obey the generalized Poisson criterion (dashed curve). The maximum packing fraction on the solid curve is about 78.4% and is obtained for $v_\bot =18.1^{\circ}.$ The four vertical lines indicate the helical pitch angles calculated for the four structures γ-, π-, α-, and 3₁₀-helices, from left to right, respectively

2.8 Helical polypeptide backbones

In the original paper on the α-helix, Pauling et al. [16] suggested a γ-helical structure in addition to the α-helix. In a commemorative article, Eisenberg [17] elucidates how the success of Pauling, Corey and Branson was furthered by their chemical insight into the planar nature of the peptide unit and from the rather strict requirements they used for the hydrogen bonds, as well as from their willingness to consider incommensurate helices (e.g. helices with no, or with relatively long repeating crystallographic unit cells). A way to enumerate the different helical structures of the polypeptide backbone is by the number, j, of peptide units that the hydrogen bond spans when the backbone binds to itself. Because of the discreteness of this self-binding only a discrete number of helices are possible. The four helices we are considering here have j = 3, 4, 5, and 6, corresponding to the 3₁₀-helix, α-helix, π-helix, and γ-helix, respectively. We wish to compare these structures to the tube model. This leads us to consider the question of how to represent the polypeptide backbone by a helical line. The absolute determination of the helical pitch, H, is straightforward. For the determination of the helical radius, a, there is no unique way to go forward; any choice taken will influence the results to be obtained. One could fit a helical line to a detailed model of the electronic density of the chain molecule in order to obtain the helical radius a. But such an approach counter the simplicity of the considerations of this paper. Instead, we will choose to let the polypeptide backbone be represented by the C ^α atoms. In Fig. 4 the pitch angles calculated for the four structures are indicated by four vertical lines, and in Table 1 the numbers are listed. For j = 4, i.e. the α-helix, the structure’s agreement with optimum packing is quite striking, and it is consistent with α-helices being the prevailing helical structure of polypeptides. The discussion on the γ-structure is somewhat archaic now, though we find it interesting that a close-packing criterion could have distinguished between the α and γ helical structures suggested by Pauling et al. [16]; the other helical structures were dismissed on the basis of implausible chemical bonding configurations.

Table 1 Helical polypeptide backbone structures: j is the number of peptide units spanned by the hydrogen bonds, n is number of residues per turn, Ω _r is the rotational twist per residue, H _r is the raise per residue, h is the reduced helical pitch, a is the helix radius (here chosen to be at the positions of the C^α atoms), $v_\bot$ is the calculated helical pitch angle, f _V the calculated volume fraction for a packed helix, f _V /f ^* _V the relative volume fraction compared to the ideal packed structure (f ^* _V  = 0.784)

3 Double helix

For a symmetric double helix the situation is very similar to the one for single helices; there are open double helices, see Fig. 5a, there are packed double helices, see Fig. 5b, there are twisted double helices, see Fig. 5c, and there are tightly packed double helices, see Fig. 5d. In the following we will investigate the geometrical constraints for packings where two identical helices are wrapped on the same cylinder.

Fig. 5

Symmetrical double helices consisting of two identical helical tubes with tube diameter D. a Two open helices on a cylinder of radius a; the repetition length is H = 2πh. b Packed helices. In this case the distance from the center line to the neighboring center line is equal to the diameter D of the tube. c Twisted double helices with a minimal value of a for a particular pitch angle (here 69°). d Tightly packed double helix. The helix has a pitch angle of 45°

The symmetric (infinite) double spirals have the parametric equations,

$$ \mathbf{r}_1 = (a\cos t_1, a\sin t_1, ht_1) $$

(10)

$$ \mathbf{r}_2=(a\cos t_2, a\sin t_2, ht_2+\pi h) $$

(11)

for $t_1,t_2\in {\bf R}.$ Consider two points on such a double helix with coordinates $\mathbf{r}_1 = (a, 0, 0)$ and $\mathbf{r}_2=(a\cos t, a\sin t, h t+\pi h).$ The square of their distance is

$$ D_{2}^2=|\overrightarrow{r_1r_2}|^2 = a^2(\cos t-1)^2 + a^2\sin^2 t + (\pi h+ht)^2; $$

(12)

the derivative of D ²₂ is

$$ {\frac{{\rm d}}{{\rm d}t}}|\overrightarrow{r_1r_2}|^2=2a^2\sin t +2\pi h^2 + 2h^2t. $$

(13)

The local minima of D ₂ are among the solutions to the following equation; compare it with Eq. (8):

$$ \sin t+{\frac{h^2}{a^2}}t +\pi{\frac{h^2}{a^2}}=0. $$

(14)

The solutions can be seen in Fig. 6. The double helix is packed when D ₂ = D, where D is the diameter of the tubes around the two backbones. The condition for packing can be seen from Fig. 7 where it can be observed that the generalized Poisson criterium is not for any helix angle a limiting factor. From the figure it can be seen that twisted double helices, Fig. 5c, with a structure that minimizes 2a/D can be obtained for $v_{\bot}= 45^{\circ}$ and larger angles. The v _tp  = 45° solution corresponds to the tightly packed double helix. This double helix can be found in Ref. [4].

Fig. 6

Solutions $(t,v_{\bot})$ of the transient equation (14) for a double helix. The solutions are symmetric under t + π → −(t + π). The maximum value of $v_{\bot}$ for nontrivial solutions is 45°

Fig. 7

Double helix. Minimum values of 2a/D plotted as function of pitch angle $v_\bot.$ The values for the packed helical structures are shown by the solid curve. The minimum values of 2a/D which obey the generalized Poisson criterion is shown as the dashed curve; as it is always below the solid curve the generalized Poisson criterion is never the one limiting the packing. The dotted curve is the packed double helices with minor and major grooves for Δ = 0.21

3.1 Close-packed double helices

The efficiency of the utilization of volume can be found using a cylindrical reference volume with diameter 2a + D which circumscribes the double helix. For a double helix the fraction of volume occupied then becomes

$$ f_V=2 \left( 1+\left( {\frac{a}{h}}\right)^2 \right)^{1/2} \left({\frac{2a}{D}}+1\right)^{-2}. $$

(15)

This volume fraction is shown in Fig. 8 as a function of the pitch angle $v_{\bot}.$ Its maximum value is approximately f ^* _V  = 0.769 found for $v_\bot^*$ about 32.5°. The result that $v_\bot^* < v_{tp}$ means that it is more efficient to allow for a central channel (of space not filled by the two helical tubes) than to select the tightly packed double helix ($v_\bot = 45^{\circ})$ when space is to be efficiently used. For the optimum close-packed double helix the channel radius is about 17% of a; if a = 7 Å then the channel width is about 2.4 Å.

Fig. 8

Volume fraction f _V for the symmetric packed double helices with Δ = 0 (solid curve). The maximum packing fraction on the solid curve is 0.796 and is obtained for $v^{*}_\bot$ about 32.5°. Also shown is the volume fraction for the case Δ = 0.21 (dotted line). For this case, the densest packing is 0.597 and is obtained for $v^*_\bot$ about 38.5°. The three vertical lines indicate the helical pitch angles calculated for the A, B, and Z forms of DNA, from left to right, respectively

3.2 Minor and major grooves

Some double helices have a broken symmetry such as the B form of DNA, which results in a minor and a major groove. They can be modeled in the same fashion as above if one introduces a phase shift Δ as an order parameter for the symmetry breaking. The transient equation then becomes

$$ \sin t+{\frac{h^2}{a^2}}t +(1-\Updelta) \pi {\frac{h^2}{a^2}}=0. $$

(16)

In Fig. 9 the solutions are shown for Δ = 0.21, which approximately corresponds to the B form of DNA. In Fig. 7 is also shown the result for 2a/D when Δ = 0.21, and in Fig. 8 the packing fraction f _V as a function of $v_{\bot}.$ As can be observed the densest packed structure appears for $v^*_{\bot}$ around 38.3° and is about f ^* _V  = 0.597.

Fig. 9

Solutions $(t,v_{\bot})$ of the transient equation (16) for a double helix with major and minor groove (Δ = 0.21). This value of Δ is about the same as for B-DNA. The first hairpin has a maximum value of $v_{\bot} = 35.4^{\circ}$

3.3 Polydeoxyribonucleotides

There are several different helical structures of DNA, here we compare the above results with the structures of double stranded A-, B-, and Z-DNA. For each of these the helical pitch, H, is well defined and easy to obtain from the literature. The arduous question is how to represent the molecular structure with helical lines. For DNA, the helical backbones are often represented by the phosphorus atoms. The phosphorus atom sits distinctly in the peripheral of the structure and can therefore not be said to be an approximate locator for the helical tubes. As a qualified first guess of the position of the helical lines we shall take a point 2.5 Å closer to the central line. This estimate is the basis for the numbers reported in Table 2, and for the calculated pitch angles which are shown in Fig. 8 as vertical lines. From Table 2 one can see that A and B DNA both are near the optimum close-packed structures when the symmetry breaking in B DNA is taken to be a priori.

Presumably, there is chemical insight to be obtained from noticing that the absolute packing ratios for B and Z DNA are nearly identical. One could speculate that this would allow the two structures to change into each other without much change in their hydration state. I.e. their hydration would involve the same, or near the same, numbers of water molecules. Even if the hydration is changed, there is little volume swelling (or contraction) involved in the transition.

Table 2 DNA structures: helical pitch angle and estimates of the fraction of volume occupied

4 Conclusion

We have calculated some simple requirements for packing of single and double helices and demonstrated the geometrical constraints that lead to specific limitations for the helical line. Tight helices can in certain cases be obtained, while open helices in others, governed by the maximum value of the pitch angle $v_{\bot}$ for which there are nontrivial self-interactions. The helices are specified by their pitch angle, $v_\bot,$ cylinder radius, a, and tube diameter, D. We define an enclosing cylinder and consider its measure of volume as an indicator of how closely packed the helices are.

Certain helical structures have more efficiently packed volumes than others and we have calculated the close-packed structures for some simple cases, including the double helix with minor and major grooves. Table 3 summarizes these results. It is remarkable how close the two prevalent molecular motives, α-helix and the B form of DNA are to these numbers. At first it might seem surprising that tiny fractions of changes in f _V can be determinative between different choices, e.g. between the prevailing α-helix and non-existing γ-helix. The 3₁₀-helix should be prohibited by the generalized Poisson criterion; this could be a contributing factor to why it is only seen in very short segments, so short that the above conservation of volume considerations are not directly applicable.

Perhaps counter to intuition, the central cylindrical cavity often seen in helical molecules is found to be a feature native of being close-packed, i.e. of optimizing space used. Such channels are common in double helices, e.g. A RNA [21].

Table 3 Close-packed single and double helices: Δ measures the symmetry breaking between major and minor grooves, $v_\bot$ is the helical pitch angle, 2a/D is the ratio of the diameters of the cylinder with the helical line and diameter of the helical tubes, A is the aspect ratio of the height to the width of the circumscribing cylinder, $A=H/(2a+D)=(2a/D) \pi \tan v_\bot/((2a/D)+1),\; f^*_V$ the volume fraction

One message to take home from this study is the importance of density. This is not surprising as density plays an important role in many of the inter-molecular interactions such as electrostatic, overlap forces, and London forces. Curiously, one could also notice that perhaps the significant role of density is one of the reasons that the application of density functional theory has become such a successful tool for molecular modeling [22].

The examples in this paper have been from the world of chain molecules; this type of considerations can perhaps be applied at larger length-scales, such as the coiling of DNA on histones, tertiary structures of proteins, carbon nanotubes, collagen, keratin, cellulose, cotton, hair, and plants.