Composite finite elements for the approximation of PDEs on domains with complicated micro-structures

Summary.

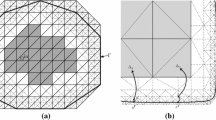
Usually, the minimal dimension of a finite element space is closely related to the geometry of the physical object of interest. This means that sometimes the resolution of small micro-structures in the domain requires an inadequately fine finite element grid from the viewpoint of the desired accuracy. This fact limits also the application of multi-grid methods to practical situations because the condition that the coarsest grid should resolve the physical object often leads to a huge number of unknowns on the coarsest level. We present here a strategy for coarsening finite element spaces independently of the shape of the object. This technique can be used to resolve complicated domains with only few degrees of freedom and to apply multi-grid methods efficiently to PDEs on domains with complex boundary. In this paper we will prove the approximation property of these generalized FE spaces.