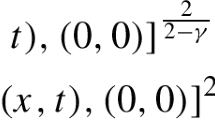Abstract
Infinite-dimensional Newton methods can be effectively used to derive numerical proofs of the existence of solutions to partial differential equations (PDEs). In computer-assisted proofs of PDEs, the original problem is transformed into the infinite-dimensional Newton-type fixed point equation \(w = - {\mathcal {L}}^{-1} {\mathcal {F}}(\hat{u}) + {\mathcal {L}}^{-1} {\mathcal {G}}(w)\), where \({\mathcal {L}}\) is a linearized operator, \({\mathcal {F}}(\hat{u})\) is a residual, and \({\mathcal {G}}(w)\) is a nonlinear term. Therefore, the estimations of \(\Vert {\mathcal {L}}^{-1} {\mathcal {F}}(\hat{u}) \Vert \) and \(\Vert {\mathcal {L}}^{-1}{\mathcal {G}}(w) \Vert \) play major roles in the verification procedures . In this paper, using a similar concept to block Gaussian elimination and its corresponding ‘Schur complement’ for matrix problems, we represent the inverse operator \({\mathcal {L}}^{-1}\) as an infinite-dimensional operator matrix that can be decomposed into two parts: finite-dimensional and infinite-dimensional. This operator matrix yields a new effective realization of the infinite-dimensional Newton method, which enables a more efficient verification procedure compared with existing Nakao’s methods for the solution of elliptic PDEs. We present some numerical examples that confirm the usefulness of the proposed method. Related results obtained from the representation of the operator matrix as \({\mathcal {L}}^{-1}\) are presented in the “Appendix”.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we study a new approach to proving the existence of solutions to elliptic problems. The proposed approach offers an improvement over existing Nakao’s methods that use a finite-dimensional projection, that is, FN and IN methods in [11] and [9, Part I]. Particularly, an important aspect of our approach is the formulation using the Schur complement without direct estimates of an inverse of the linearized operator. Our approach inherits the advantages of both Nakao’s FN and IN methods using a finite-dimensional projection, which also indicates that the disadvantages of both methods are resolved.
We consider computer-assisted existence proofs for the nonlinear elliptic boundary value problem
where \(\varOmega \subset {\mathbb R}^n (n = 1,2,3)\) is a bounded domain with a Lipschitz boundary, and \(f:H^1_0(\varOmega ) \rightarrow H^{-1}(\varOmega )\) is a given nonlinear function which is assumed to be Fréchet differentiable. Equation (1) is a basic case of a semi-linear elliptic partial differential equation (PDE), for which many computer-assisted proof methods have been developed [4,5,6, 8,9,10,11, 13,14,17]. These methods are intended to prove the existence of solutions based on the fixed point theorem in Sobolev spaces. Throughout this paper, \( H^1(\varOmega ) \) is defined as the first-order \( L^2 \) Sobolev space, \( H^1_0(\varOmega ) := \{ u \in H^1(\varOmega ) : u = 0~\text{ on } ~ \partial \varOmega \} \) with the inner product \((u, w)_{H^1_0}:=(\nabla u, \nabla w)_{L^2}\), and \( H^{-1}(\varOmega ) \) is the topological dual of \( H^1_0(\varOmega )\). We now categorize the verification methods developed to date to clarify the significance and advantages of the method described in this paper:
-
FN method: Applies Newton’s method only for the finite-dimensional part (e.g., FN-Int [5, 6, 9, 11], FN-Norm [9,10,11]).
-
IN method: Uses the infinite-dimensional Newton method (e.g., Newton–Kantorovich-like theorem [9, 15,16,17], IN-Linz [8, 9, 11, 13], Newton–Kantorovich theorem [18]).
In the FN method, with an appropriate setting of the finite-dimensional subspace \(V_h \subset H^1_0(\varOmega )\), we first consider the Ritz projection \(R_h : H^1_0(\varOmega ) \rightarrow V_h\) defined as
for \(u \in H^1_0(\varOmega )\), where I denotes the identity operator on \(H^1_0(\varOmega )\). As a property of \(R_h\), we assume that there exists a positive constant C(h) which can be numerically estimated satisfying
with the property that \(C(h) \rightarrow 0\) as the parameter \(h \rightarrow 0\). Using this projection, the problem is decomposed into two parts: finite-dimensional and infinite-dimensional. Let \(\psi _1, \! \ldots , \! \psi _N \) be a basis of \(V_h\), and let \(V_\bot := \{ u \in H^1_0(\varOmega ) ~ | ~ (u, v_h)_{H^1_0} = 0, ~ v_h \in V_h \}\) be an orthogonal complement of \(V_h\). For a given approximate solution \(\hat{u} \in V_h\), setting \(w := u - \hat{u}\), \(w_h := R_h w\), and \(w_\bot := (I - R_h)w\), the FN method uses the following fixed point formulation:
find \(w_h \in V_h, ~ w_\bot \in V_\bot \) satisfying
where \({\mathcal {A}}: H^1_0(\varOmega ) \rightarrow H^{-1}(\varOmega )\) is equal to minus the weak Laplace operator. In [4], the candidate set of solutions was set to
and the fixed point theorem was applied to (3) to verify a solution in the set \(W= W_h + W_\bot \). To confirm the verification condition in the fixed point theorem, the verified computation of solutions for a linear system of equations and the constructive a priori error estimates (2) for the Ritz projection play an essential role. This was the first approach to numerical verification, but is based on a contraction assumption which is more restrictive compared with the FN method.
The FN method applies Newton’s method to the finite-dimensional part of (3) as follows:
Let \(f'[\hat{u}]\) be the Fréchet derivative at \(\hat{u}\) of the nonlinear term f(u), and let \({\mathcal {L}}: H^1_0(\varOmega ) \rightarrow H^{-1}(\varOmega )\) be a linear operator defined as
Furthermore, the finite-dimensional operator \(T : V_h \rightarrow V_h\) is defined as
and T is assumed to be invertible. Then, we can rewrite the finite-dimensional part of (3) as
This FN method was developed in [5], and it has been confirmed that Newton’s method is more effective for the verification of \(w_h\) than the method in [4]. Additionally, because the computation of \(w_h\) by the iterative use of (8) is sufficient to simply solve the linear system of equations, the cost is not large compared with the matrix norm estimation of \(T^{-1}\). However, when f(u) includes the first-order derivative \( \nabla u\), because of the property of interval arithmetic, it sometimes causes unexpected inefficiencies in the estimation of the right-hand side of (8); that is, the inefficiency appears as a result of the effect of the corresponding estimation of \(\nabla w_{\perp }\) and leads to the failure of verification because of an explosive expansion of intervals in the iteration (e.g., see [9, 10]). This implies that the effect of Newton’s method on \(w_{\perp }\) has not been achieved. To overcome this difficulty, in [9, 10], the FN-Norm method was introduced. This ensures a more effective verification procedure by setting the candidate set \( W_h \) of the finite-dimensional part to
By contrast, the IN method assumes that the linearized operator \({\mathcal {L}}\) is invertible and considers the following fixed point equation:
find \(w \in H^1_0(\varOmega )\) such that
where
and
As (9) is a Newton-type formulation in the infinite-dimensional sense, the linear term with respect to w, which is a shortcoming of the FN method, is no longer present on the right-hand side of the equation. Therefore, a Newton–Kantorovich-like theorem can be derived using the fixed point equation (9). However, as the inverse operator \({\mathcal {L}}^{-1}\) cannot be calculated directly, it is necessary to show the invertibility of \({\mathcal {L}}\) and estimate the operator norm \(\Vert {\mathcal {L}}^{-1} \Vert \). Thus, the evaluation of \(|| {\mathcal {L}}^{- 1} ||\) is the major task in the verification procedures of the IN method, and has been studied by many researchers since 1991. For example, [3, 8, 12, 13, 19,20,21,22] and [9, Part I] used the Ritz projection \(R_h\) and the projection error bound C(h) by limiting \(\varOmega \) to bounded domains. Other methods exist that avoid the Ritz projection \(R_h\) and its error bound C(h), and hence can be applied even for unbounded domains \(\varOmega \), where the projection error bound C(h) is not accessible or does not even exist (e.g., [14,15,16] and [9, Part II]). IN methods that do not need a projection error bound and methods that use projection error bounds have strengths and weaknesses, and a comparison of their qualities on a general level is impossible. Generally, the IN method defines the candidate set as
Therefore, the IN method overestimates the finite-dimensional parts compared with the FN method.
We now describe a new approach that incorporates the advantages of both Nakao’s FN and IN methods using the Ritz projection \(R_h\) in [11] and [9, Part I]. In this paper, we essentially consider the IN method based on (9), but we propose a verification method without estimating the norm \(\Vert {\mathcal {L}}^{-1} \Vert \). Through a computational procedure that avoids the direct evaluation of the operator norm \(\Vert {\mathcal {L}}^{-1} \Vert \), highly accurate and efficient verification can be expected. We decompose (9) into finite-dimensional and infinite-dimensional parts; that is, \((w_h, w_\bot )^T \in V_h \times V_\bot \) such that
However, we cannot directly calculate \({\mathcal {L}}^{-1}\) for the same reason as for the existing IN method. To overcome this difficulty, we introduce an operator matrix, whose existence will be proved later,
satisfying
Here, we apply the fixed point theorem to the following equation:
with candidate sets (4) and (5). Note that the right-hand side of this fixed point equation no longer has linear terms in \(w_h\) nor \(w_\bot \). Therefore, the proposed method overcomes the disadvantages of the FN method. Additionally, note that we can directly compute the finite-dimensional part (e.g., \(H_{11}R_h {\mathcal {A}}^{-1} {\mathcal {F}}(\hat{u})\)) by solving the linear system of equations, which is an advantage of the FN method. Therefore, the proposed method also overcomes the disadvantages of the IN method. Thus, our approach inherits the advantages of both Nakao’s FN and IN methods using a finite-dimensional projection in [11] and [9, Part I], which also indicates that the disadvantages of both methods are resolved; that is, the disadvantage of the Newton method not working for the infinite-dimensional part of the FN method and the disadvantage of the poor computational efficiency of the finite-dimensional part in the IN method are removed. For the actual implementation of the verification procedure, it is necessary to obtain a more detailed form of the operator matrix H. Thus, we consider a specific construction of this matrix below.
The remainder of this paper is organized as follows: In Sect. 2, we describe how to construct the operator matrix H. In Sect. 3, we present the results of numerical experiments using the operator matrix H. We also describe why the proposed method offers an improvement over previous techniques based on some useful results in the “Appendix”.
2 Constitution of the inverse operator matrix H
In this section, we present a detailed description of the actual construction of the operator matrix H satisfying (14) and (15). The basic idea comes from the concept of block Gaussian elimination and its corresponding ‘Schur complement’ for matrix problems.
We consider a solution \(\phi \) that satisfies the linear equation
for a given \(g \in H^{-1}(\varOmega )\). We denote
We multiply \({\mathcal {A}}^{-1}\) from the left on both sides of (17), and decompose the result into the finite and infinite-dimensional parts using the Ritz projection \(R_h\) as follows:
where \(I_{V_{\bot }}\) is the identity operator on \(V_{\bot }\). Furthermore, transforming the above equation using the operator matrix yields
Let \(Y: V_{\bot } \rightarrow V_h\), \(Z: V_h \rightarrow V_{\bot }\), and \(G: V_{\bot } \rightarrow V_{\bot }\) be bounded linear operators defined as
respectively. Additionally, we define the \(2 \times 2\) block operator matrix D as
Moreover, if the operators \({\mathcal {L}}\) and D are invertible, then we have
and H is equal to \(D^{-1}\) from (15).
We first present a sufficient condition for the invertibility of the operator D, which also provides a detailed expression for \(D^{-1}\).
Lemma 1
The finite-dimensional operator \(T : V_h \rightarrow V_h\) defined as (7) is assumed to be invertible. Let \(S: V_{\bot } \rightarrow V_{\bot }\) be a linear operator defined as
which is the so-called Schur complement corresponding to the operator T of the block operator matrix D. If S is bijective, then the operator D defined by (20) is also bijective and we have
where
where \(I_{V_h}\) is the identity operator on \(V_h\).
Proof
. We first apply block Gaussian elimination to the operator matrix D. We multiply \(M_1\) from the left of D as follows:
This procedure is so-called block forward elimination. Next, we multiply \(M_2\) from the left of \(M_1 D\) as
From the assumption that T and S are bijective, we have
Note that the multiplication of \(M_3 M_2\) corresponds to so-called back substitution.
Next, to show that \(M_3 M_2 M_1\) is \(D^{-1}\), we multiply \(M_3 M_2 M_1\) from the right of D as follows:
Thus, \(M_3 M_2 M_1 = D^{-1}\) is proved. \(\square \)
We obtain the inverse operator of D using Lemma 1. However, the operator matrix H satisfying (15) cannot be introduced without the invertibility of \({\mathcal {L}}\). Therefore, the following theorem provides a sufficient condition for the invertibility of \({\mathcal {L}}\).
Theorem 1
Under the same notation and assumptions as in Lemma 1, the linearized operator \({\mathcal {L}}\) defined by (6) is bijective, and the operator matrix H satisfying (15) is given by
Proof
We show that the linearized operator \({\mathcal {L}}\) is bijective. From the assumptions and Lemma 1, we have an inverse operator of D. Multiplying \(D^{-1}\) from the left of (18), we obtain
To prove that \({\mathcal {L}}\) is injective, we show that \(\phi = 0\) is the only solution of the equation \({\mathcal {L}} \phi = 0\). This can be readily seen from the fact that, using the bijectivity of operators D and \({\mathcal {A}}\), the solution of (18) with \(g = 0\) implies that \(\phi = 0\).
Finally, we prove that the linearized operator \({\mathcal {L}}\) is surjective. For this, it is sufficient to show that there exists a solution \(\phi \in H^1_0(\varOmega )\) satisfying \({\mathcal {L}} \phi = g\) for any \(g \in H^{-1}(\varOmega )\). Now, for \(g \in H^{-1}(\varOmega )\), define \(( \phi _h, \phi _{\bot })^T\) as the left-hand side of (22) and set \(\phi := \phi _h + \phi _{\bot }\). Then, by the invertibility of the operator matrix H, the function \(\phi \) satisfies (18), and therefore it also implies (17), which proves the desired surjectivity. Thus, the operator \({\mathcal {L}}\) is bijective. \(\square \)
Theorem 1 provides a specific expression of the operator matrix H satisfying (14). Moreover, Theorem 1 provides a new expression for the solution \(\phi \) of the linear noncoercive elliptic PDE \({\mathcal {L}} \phi = g\). Therefore, for example, the exact expression of the Ritz projection error for the solution of the linear noncoercive elliptic PDE \({\mathcal {L}} \phi = g\) is also derived from Theorem 1 (see Appendix C for details).
At the end of this section, we describe how to verify that T and S in the assumptions of Theorem 1 are invertible operators. Let \({\mathbf {G}} \in {\mathbb R}^{N \times N}\) be a real matrix defined as \(( {\mathbf {G}} )_{i, j} := ( \nabla \psi _j, \nabla \psi _i)_{L^2} - (f'[\hat{u}] \psi _j, \psi _i)_{L^2}\). Then, the matrix \({\mathbf {G}}\) is invertible if and only if T is the invertible operator (e.g., [9, Lemma 2.1, p.44]). Therefore, by confirming the invertibility of the matrix \({\mathbf {G}}\) using numerical computation with guaranteed accuracy, we can easily check the invertibility of T.
To confirm the invertibility of the operator S, the following operator norm is used. For two Banach spaces X and Y, the set of bounded linear operators from X to Y is denoted by L(X, Y) with the operator norm \(\Vert {\mathcal {B}} \Vert _{ L(X, Y) } := \sup \{ \Vert {\mathcal {B}} u \Vert _{Y}/\Vert u \Vert _{X} : {u \in X \setminus \{0\}}\} \) for \({\mathcal {B}} \in L(X, Y)\). When \(X = Y\), we simply use L(X). Then, we can confirm the invertibility of S using the following well-known theorem.
Lemma 2
Let S be a bounded linear operator satisfying (21). Setting \(\kappa := \Vert {\mathcal {A}}_{\bot }^{-1} f'[\hat{u}] |_{V_\bot } + {\mathcal {A}}_{\bot }^{-1} f'[\hat{u}] |_{V_h} T^{-1} {\mathcal {A}}_h^{-1} f'[\hat{u}] |_{V_\bot } \Vert _{L(V_\bot )}\), if \(\kappa < 1\) holds, then S is bijective and its norm satisfies
Proof
The Ritz projection \(R_h\) is a continuous projection; therefore, \(V_h\) and \(V_{\bot }\) are Hilbert spaces with the inner product \((\cdot , \cdot )_{H^1_0}\), respectively. The definition \(S := I_{V_\bot } - {\mathcal {A}}_{\bot }^{-1} f'[\hat{u}] |_{V_\bot } - {\mathcal {A}}_{\bot }^{-1} f'[\hat{u}] |_{V_h} T^{-1} {\mathcal {A}}_h^{-1} f'[\hat{u}] |_{V_\bot }\) and the assumption \(\kappa < 1\) yield the bijectively of S as a result of the well-known theory of the Neumann series. \(\square \)
To compute the constant \(\kappa \), we use the inequality (2) and the Aubin–Nitsche trick
There are several ways to compute the constant \(\kappa \). For example, in the case of \(f'[\hat{u}] \in L(L^2(\varOmega ))\), we define the constants \(C_{f,L^2}\) and \(\tau _{L^2}\) as
Then, we can estimate \(\kappa \) as
Note that \(\tau _{L^2}\) can be estimated as the matrix norm \(\Vert {\mathbf {L}}^{\frac{1}{2}} {\mathbf {G}}^{-1} {\mathbf {L}}^{\frac{T}{2}} \Vert _{E}\) induced by the Euclidean vector norm, where \({\mathbf {L}}^{\frac{1}{2}}\) is the Cholesky factorization of the matrix \({\mathbf {L}}\), which is defined as \(({\mathbf {L}})_{i,j} := (\psi _j, \psi _i)_{L^2}\).
If \(f'[\hat{u}]\) is in \(L(H^1_0(\varOmega ), L^2(\varOmega ))\), we define the constants \(C_{f}\), \(C_{f, \bot }\), and \(\tau _{L^2,H^1_0}\) as
where \(\tau _{L^2,H^1_0}\) can be also estimated using verified computing (e.g., see [9, (3.63), p.93]). Then, we can estimate \(\kappa \) as
The estimation (24) is the same as [9, (3.64), p.93]. It is also possible to derive an evaluation similar to [9, (3.46), p.89] from Lemma 2. Moreover, since C(h) has the property that \(C(h) \rightarrow 0\) as \(h \rightarrow 0\), it is expected to satisfy the sufficient condition \(\kappa < 1\).
3 Numerical examples
3.1 Verification procedure
In this subsection, we describe a verification procedure to realize computer-assisted proofs using the fixed point formulation (16) with the operator matrix H. The proposed verification method is a combination of the FN and IN methods developed above.
Let \(\hat{u} \in V_h \subset H^1_0(\varOmega )\) be a solution that satisfies the following equation:
For example, \(\hat{u}\) may be obtained by numerical computations with guaranteed accuracy for finite-dimensional nonlinear equations, such as the Krawczyk method. Note that \(R_h {\mathcal {A}}^{-1} {\mathcal {F}}(\hat{u})\) in (16) becomes zero.
Next, we verify that the matrix \({\mathbf {G}}\) defined as \(( {\mathbf {G}} )_{i, j} := ( \nabla \psi _j, \nabla \psi _i)_{L^2} - (f'[\hat{u}] \psi _j, \psi _i)_{L^2}\) and the operator S are invertible. As Theorem 1 implies that the linearized operator \({\mathcal {L}}\) defined as (6) is invertible, we can transform problem (1) into the fixed point equation (16) using the operator matrix H.
Schauder or Banach’s fixed point theorem may be applied to the equation (16) with the candidate sets (4) and (5), as in [4, 5]. Here, the fixed point theorem may be selected as follows. If the nonlinear term f(u) is similar to that in [15] (e.g., \(f(u) \in L^2(\varOmega )~ \forall u \in H^1_0(\varOmega )\)), then because \({\mathcal {L}}^{-1} {\mathcal {G}}\) is a compact operator, Schauder’s fixed point theorem can be used. If this is not the case, or if we need to prove the local uniqueness of the solution, it is preferable to use Banach’s fixed point theorem. A survey of the FN method [6] makes it easy to select the appropriate method.
3.2 Example
In this subsection, we present an example in which our method is used to verify a solution of the elliptic boundary value problem
with \(\varOmega = (0,1)^2\). This is Emden’s equation, which is a good test problem for comparing the proposed method with other approaches. Additionally, because the results for \(\rho \) in (12) given by many existing IN methods [8, 15, 16, 18] are almost the same, it is not necessary to compare numerous existing IN approaches. Emden’s equation has also been discussed in terms of the FN method [23].
All computations were implemented on a computer with 2.20 GHz Intel Xeon E7-4830 v2 CPU \(\times \) 4, 2 TB RAM, and CentOS 7.2 using C++11 with GCC version 4.8.5. All rounding errors were strictly estimated using kv library [1]. This guarantees the mathematical correctness of all the results.
We constructed approximate solutions for (26) using a Legendre polynomial basis. Specifically, we defined the set \(\{ \psi _1, \psi _2, \ldots \psi _N \}\) of Legendre polynomials as
with
and defined the finite-dimensional subspace as a tensor product
See [2] for information on how to compute C(h) in (2) corresponding to the Legendre polynomial basis. Then, \(\hat{u} \in V_h^N\) satisfying the finite-dimensional nonlinear problem (25) can be written as
where \(\hat{u}_{i,j}\) are real numbers. Note that, in a real computation, \(\hat{u}_{i,j}\) are obtained as intervals that include the exact solution of (25) using the Krawczyk method. For example, when \(N=10\), a solution \(\hat{u}\) satisfying (25) can be obtained (see Table 1). Here, \(1.23_{456}^{789}\) denotes the interval [1.23456, 1.23789]. As the solution has symmetry, note that \(\hat{u}_{i,j}\) is zero when i and j are even. Under this setting, exact solutions \(\hat{u} \in V_h^{10}\) satisfying (25) were computed numerically. Their graphs are displayed in Fig. 1. The computational results of the constants C(h) and \(\kappa \) using (23) were 0.037268163011998514 and 0.31088290279527165, respectively. Therefore, because \(\kappa < 1\), the operator S was bijective. Thus, taking the candidate set as
the method proposed in this paper succeeded in the numerical verification of problem (26). The verified \(W_h\) results for the finite-dimensional parts are presented in Tables 1 and 2, and the \(\alpha \) results for the infinite-dimensional parts are given in Table 2. Furthermore, we can prove that the exact solution \(u^*\) of (26) exists in \(\hat{u} + W_h + W_\bot \), and we can estimate
FN-Int (e.g., [5, 6, 11]) was also applied using similar candidate sets (27) and (28) and performing a detailed evaluation of the finite-dimensional and infinite-dimensional parts. However, as FN-Int only applies Newton’s method to the finite-dimensional parts, the verification failed for \(N=10\), which implies that \(N=10\) was too small to achieve a successful verification.
As the error bound of the form \(\Vert u^* - \hat{u} \Vert _{H^1_0} \le \rho \) was obtained in the course of a successful verification by the IN method for \(N=10\), we compared the proposed method with the IN method [8, 18] from this viewpoint in Table 2. It is clear from the table that the value of \(\rho \) given by the proposed method was smaller than that produced by the existing IN method [8, 18]. Additionally, as described in Sect. 3.1, because we partially incorporated the detailed calculations of the IN method into the proposed method, enhancing the IN method could lead to improvements to the results of the proposed method. The reason why the proposed method produced smaller values of \(\rho \) than [8, 18] is discussed in Appendix B.
Approximate solution of (26) (\(N=10\))
From Table 1, which presents results for \(N = 10\), the error interval of the finite-dimensional part appears to be rather large. This is because N was too small. In fact, very sharp results were obtained in the case of \(N = 40\) (see Tables 3 and 4). Additionally, we obtained \(C(h) = 0.01150109366291357\) and \(\kappa = 0.029612643887446451\) using (23). Because C(h) was smaller than the case of \(N = 10\), the constant \(\kappa \) was also small . Here, \(\pm 1.23_{456}^{789} \times 10^{-11}\) denotes the interval \([-1.23456 \times 10^{-11}, 1.23789 \times 10^{-11}]\).
4 Conclusion
In this paper, we described a new formulation (16) for the numerical proof of the existence of solutions for elliptic problems. The proposed approach has advantages over both Nakao’s FN and IN methods using the Ritz projection \(R_h\) in [11] and [9, Part I]. In particular, we derived a specific formula for the operator matrix H, which is needed to compute (16), in Theorem 1. As a result, while using the infinite-dimensional Newton method, the error evaluation for each coefficient interval of the finite basis is also enclosed, as demonstrated by the results in Tables 1 and 3. This is considered an advantage of the FN method. Furthermore, the proposed method produced better results than the IN method [8, 18], even for the norm estimation, as demonstrated in Tables 2 and 4.
References
Kashiwagi, M.: kv library (2016). http://verifiedby.me/kv/index-e.html
Kimura, S., Yamamoto, N.: On explicit bounds in the error for the \( H_0^1 \)-projection into piecewise polynomial spaces. Bull. Inf. Cybern. 31(2), 109–115 (1999)
Kinoshita, T., Watanabe, Y., Nakao, M.T.: An alternative approach to norm bound computation for inverses of linear operators in Hilbert spaces. J. Differ. Equ. 266(9), 5431–5447 (2019)
Nakao, M.T.: A numerical approach to the proof of existence of solutions for elliptic problems. Jpn. J. Appl. Math. 5(2), 313–332 (1988)
Nakao, M.T.: A numerical approach to the proof of existence of solutions for elliptic problems ii. Jpn. J. Appl. Math. 7(3), 477 (1990)
Nakao, M.T.: Numerical verification methods for solutions of ordinary and partial differential equations. Numer. Funct. Anal. Optim. 22(3–4), 321–356 (2001)
Nakao, M.T., Hashimoto, K.: Guaranteed error bounds for finite element approximations of noncoercive elliptic problems and their applications. J. Comput. Appl. Math. 218(1), 106–115 (2008)
Nakao, M.T., Hashimoto, K., Watanabe, Y.: A numerical method to verify the invertibility of linear elliptic operators with applications to nonlinear problems. Computing 75(1), 1–14 (2005)
Nakao, M.T., Plum, M., Watanabe, Y.: Numerical Verification Methods and Computer-Assisted Proofs for Partial Differential Equations. Springer, Berlin (2019)
Nakao, M.T., Watanabe, Y.: An efficient approach to the numerical verification for solutions of elliptic differential equations. Numer. Algorithms 37(1–4), 311–323 (2004)
Nakao, M.T., Watanabe, Y.: Numerical verification methods for solutions of semilinear elliptic boundary value problems. Nonlinear Theory Appl. IEICE 2(1), 2–31 (2011)
Nakao, M.T., Watanabe, Y., Kinoshita, T., Kimura, T., Yamamoto, N.: Some considerations of the invertibility verifications for linear elliptic operators. Jpn. J. Ind. Appl. Math. 32(1), 19–31 (2015)
Oishi, S.: Numerical verification of existence and inclusion of solutions for nonlinear operator equations. J. Comput. Appl. Math. 60(1), 171–185 (1995)
Plum, M.: Bounds for eigenvalues of second-order elliptic differential operators. Zeitschrift für angewandte Mathematik und Physik ZAMP 42(6), 848–863 (1991)
Plum, M.: Enclosures for weak solutions of nonlinear elliptic boundary value problems. In: Agarwal, R.P. (ed.) Inequalities and Applications, pp. 505–521. World Scientific, Singapore (1994)
Plum, M.: Existence and multiplicity proofs for semilinear elliptic boundary value problems by computer assistance. Jahresbericht der Deutschen Mathematiker Vereinigung 110(1), 19–54 (2008)
Plum, M.: Computer-assisted proofs for semilinear elliptic boundary value problems. Jpn. J. Ind. Appl. Math. 26(2–3), 419–442 (2009)
Takayasu, A., Liu, X., Oishi, S.: Verified computations to semilinear elliptic boundary value problems on arbitrary polygonal domains. Nonlinear Theory Appl. IEICE 4(1), 34–61 (2013)
Tanaka, K., Takayasu, A., Liu, X., Oishi, S.: Verified norm estimation for the inverse of linear elliptic operators using eigenvalue evaluation. Jpn. J. Ind. Appl. Math. 31(3), 665–679 (2014)
Watanabe, Y., Kinoshita, T., Nakao, M.: A posteriori estimates of inverse operators for boundary value problems in linear elliptic partial differential equations. Math. Comput. 82(283), 1543–1557 (2013)
Watanabe, Y., Kinoshita, T., Nakao, M.T.: An improved method for verifying the existence and bounds of the inverse of second-order linear elliptic operators mapping to dual space. Jpn. J. Ind. Appl. Math. 36(2), 1–14 (2019)
Watanabe, Y., Nagatou, K., Plum, M., Nakao, M.T.: Norm bound computation for inverses of linear operators in Hilbert spaces. J. Differ. Equ. 260(7), 6363–6374 (2016)
Watanabe, Y., Nakao, M.T.: Numerical verifications of solutions for nonlinear elliptic equations. Jpn. J. Ind. Appl. Math. 10(1), 165–178 (1993)
Acknowledgements
This work was supported by JST CREST Grant Number JPMJCR14D4 and MEXT under the “Exploratory Issue on Post-K computer” project (Development of verified numerical computations and super high-performance computing environment for extreme research). The second author was supported by JSPS KAKENHI Grant Number 18K03434. We thank the editors and reviewers for providing useful comments that helped to improve the content of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A Another formula for the operator matrix H
In Lemma 1 and Theorem 1, the Schur complement S (defined in (21)) for the (1, 1) element T of the operator matrix D is created and some properties are proved. We present another form of the operator matrix H using the Schur complement \(S_h: V_h \rightarrow V_h\) for the (2, 2) element \(I_{V_{\bot }} - {\mathcal {A}}_{\bot }^{-1} f'[\hat{u}] |_{V_\bot } (=: G)\) of the operator matrix D.
Lemma 3
The infinite-dimensional operator \(G: V_{\bot } \rightarrow V_{\bot }\) defined in (19) is assumed to be nonsingular. Let \(S_h: V_h \rightarrow V_h\) be a linear operator defined as
which is the so-called Schur complement corresponding to the operator G of the block operator matrix D. If \(S_h\) is bijective, then the operator D defined by (20) is also bijective and we have
where
Proof
We prove Lemma 3 in the same way as Lemma 1. We multiply \(M_1'\) from the left of D as follows:
Next, we multiply \(M_2'\) from the left of \(M_1' D\) as follows:
From the assumption that \(S_h\) and G are bijective, we have
Next, to show that \(M_3' M_2' M_1'\) is \(D^{-1}\), we multiply \(M_3' M_2' M_1'\) from the right of D as follows:
Therefore, \(M_3' M_2' M_1'\) is the bounded inverse operator of D. \(\square \)
Theorem 2
Under the same notation and assumptions as in Lemma 3, the linearized operator \({\mathcal {L}}\) defined by (6) is bijective, and the operator matrix H satisfying (15) is
Proof
This assertion can be proved in a similar manner to Theorem 1 using Lemma 3 instead of Lemma 1. \(\square \)
As we can verify the invertibility of the operator G in a similar manner to that used in Lemma 2, it is also possible to derive a verification procedure using Theorem 2 instead of Theorem 1.
Moreover, it is possible to derive, from the operator matrix D in Theorem 1, the results in previous papers [8, 12, 21] for the norm evaluation \(\Vert {\mathcal {L}}^{-1} \Vert _{L(H^{-1}, H^1_0)}\) of the inverse operator \({\mathcal {L}}^{-1}\) (see Appendix B). However, there has been no previous discussion (e.g., [9]) of the norm evaluation of the operator \( {\mathcal {L}}^{-1} \; : \; H^{-1}(\varOmega ) \rightarrow H^1_0(\varOmega )\) using the operator matrix D in Theorem 2.
Appendix B Relation between the norm \(\Vert {\mathcal {L}}^{-1} \Vert _{L(H^{-1}, H^1_0)}\) and Theorem 1
There have been many studies on the estimation of the norm \(\Vert {\mathcal {L}}^{-1} \Vert _{L(H^{-1}, H^1_0)}\) because it plays an important role in the existing IN method (e.g., [8, 9, 12,13,14,15, 19, 21]). In the following, we show that it is also possible to obtain the upper bound of the inverse operator norm \(\Vert {\mathcal {L}}^{-1} \Vert _{L(H^{-1}, H^1_0)}\) using Theorem 1.
Corollary 1
(of Theorem 1) Under the same assumptions as in Theorem 1, \({\mathcal {L}}\) is invertible, and it follows that
where \(\Vert \cdot \Vert _{E}\) denotes a matrix norm induced by the Euclidean vector norm \(| \cdot |_{E}\).
Proof
We define the norm of the direct product space \(V_h \times V_{\bot }\) as
Then, from Theorem 1, the solution \(\phi \) of the linear equation (17) can be evaluated as
Therefore, we have
Moreover, using the structure of the operator matrix H satisfying (14), we have
\(\square \)
Remark 1
The estimation of the inverse operator norm in Corollary 1 is closely related to the method used in previous studies [8, 9, 12, 21]. However, it is noted that Theorem 1 can be applied directly without using Corollary 1. For example, for the first term on the right-hand side of (9), the existing IN method evaluates
to apply Corollary 1. If \(\hat{u}\) is a solution satisfying (25), then \(R_h {\mathcal {A}}^{-1} {\mathcal {F}}(\hat{u})\) vanishes, but this is not reflected in the estimation of the norm \(\Vert {\mathcal {L}}^{-1} \Vert _{ L(H^{-1}, H^1_0) }\). By contrast, using Theorem 1 directly, we can estimate
Therefore, the estimations of \(\Vert H_{11} \Vert _{L(H^1_0)}\) and \(\Vert H_{21} \Vert _{L(H^1_0)}\) are useless in the evaluation for \(\Vert {\mathcal {L}}^{-1} \Vert _{L(H^{-1}, H^1_0)}\); that is, the proposed method is better than existing IN methods for evaluating \(\Vert {\mathcal {L}}^{-1} \Vert _{L(H^{-1}, H^1_0)}\).
The inverse operator norm \(\Vert {\mathcal {L}}^{-1} \Vert _{L(H^{-1}, H^1_0)}\) can be evaluated from Theorem 2 using the same procedure as in Corollary 1.
Corollary 2
(of Theorem 2) Under the same assumptions as in Theorem 2, \({\mathcal {L}}\) is invertible and
Appendix C An exact expression for the Ritz projection error in the solution of the noncoercive equation (17)
In this appendix, we derive an expression for the Ritz projection error \(\phi - R_h \phi \) in the exact solution \(\phi \) of the linear noncoercive elliptic PDE (17). Using this result, we can, for example, determine a constant C that satisfies the inequality \(\Vert \phi - R_h \phi \Vert _{H^1_0} \le C \Vert {\mathcal {L}} \phi \Vert _{L^2}, ~ \phi \in \{ \phi \in H^1_0 | \varDelta \phi \in L^2(\varOmega ) \}\), even though the elliptic operator \(\mathcal {L}\) is noncoercive (cf. [7]).
Corollary 3
(of Theorem 1) Under the same assumptions as in Theorem 1, the Ritz projection error of the solution \(\phi \in H^1_0(\varOmega )\) of the linear noncoercive elliptic PDE (17) is
Proof
The proof is obtained immediately from \(\phi _\bot \) in the expression of the proof for Theorem 1. \(\square \)
Using Corollary 3 as \(g \in L^2(\varOmega )\), it is easy to derive the constant C satisfying \(\Vert \phi - R_h \phi \Vert _{H^1_0} \le C \Vert {\mathcal {L}} \phi \Vert _{L^2}\) in [7].
Similarly, we can derive the following proposition from Theorem 2.
Corollary 4
(of Theorem 2) Under the same assumptions as in Theorem 2, the Ritz projection error in the solution \(\phi \in H^1_0(\varOmega )\) of the linear noncoercive elliptic PDE (17) is represented as follows:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sekine, K., Nakao, M.T. & Oishi, S. A new formulation using the Schur complement for the numerical existence proof of solutions to elliptic problems: without direct estimation for an inverse of the linearized operator. Numer. Math. 146, 907–926 (2020). https://doi.org/10.1007/s00211-020-01155-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-020-01155-7