Error estimates for a finite difference scheme associated with Hamilton–Jacobi equations on a junction

Abstract

This paper is concerned with monotone (time-explicit) finite difference scheme associated with first order Hamilton–Jacobi equations posed on a junction. It extends the scheme introduced by Costeseque et al. (Numer Math 129(3):405–447, 2015) to general junction conditions. On the one hand, we prove the convergence of the numerical solution towards the viscosity solution of the Hamilton–Jacobi equation as the mesh size tends to zero for general junction conditions. On the other hand, we derive some optimal error estimates of in $L^{\infty }_{\text {loc}}$ for junction conditions of optimal-control type.

1 Introduction

This paper is concerned with numerical approximation of first order Hamilton–Jacobi equations posed on a junction, that is to say a network made of one node and a finite number of edges.

The theory of viscosity solutions for such equations on such domains has reached maturity by now [1, 25, 26, 30, 31]. In particular, it is now understood that general junction conditions reduce to special ones of optimal-control type [25]. Roughly speaking, it is proved in [25] that imposing a junction condition ensuring the existence of a continuous viscosity solution and a comparison principle is equivalent to imposing a junction condition obtained by “limiting the flux” at the junction point.

For the “minimal” flux-limited junction conditions, Costeseque, Lebacque and Monneau [16] introduced a monotone numerical scheme and proved its convergence. Their scheme can be naturally extended to general junction conditions and our first contribution is to introduce it and to prove its convergence.

Our second and main result is an error estimate in the style of Crandall–Lions [17] in the case of flux-limited junction conditions. It is explained in [17] that the proof of the comparison principle between sub- and super-solutions of the continuous Hamilton–Jacobi equation can be adapted in order to derive error estimates between the numerical solution associated with monotone (stable and consistent) schemes and the continuous solution. In the case of a continuous equation, the comparison principle is proved thanks to the technique of doubling variables; it relies on the classical penalisation term $\varepsilon ^{-1} |x-y|^2$. Such a penalisation procedure is known to fail in general if the equation is posed on a junction, because the equation is discontinuous in the space variable; it is explained in [25] that it has to be replaced with a vertex test function. But the vertex test function used in [25] is not regular enough (the derivatives are not locally Lipschitz) to get the error estimates. So here we replace it by the reduced minimal action introduced in [26] for the “minimal” flux-limited junction conditions, i.e. the flux is not limited since $A\le A_0$ the smallest limiting parameter defined in (1.7). We study and use it in the case where the flux is “strictly limited”, i.e. $A>A_0$.

In order to derive error estimates as in [17], it is important to study the regularity of the test function. More precisely, we prove (Proposition 5.9) that its gradient is locally Lipschitz continuous, at least if the flux is “strictly limited” and far away from a special curve. But we also see that the reduced minimal action is not of class $C^{1}$ on this curve. However we can get “weaker” viscosity inequalities thanks to a result in [25] (see Proposition 2.4). Such a regularity result is of independent interest.

1.1 Hamilton–Jacobi equations posed on junctions

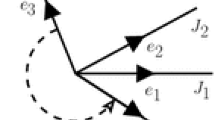
A junction is a network made of one node and a finite number of infinite edges. It can be viewed as the set of N distinct copies $(N \ge 1)$ of the half-line which are glued at the origin. Let us consider different unit vectors $e_{\alpha } \in \mathbb {R}^2$ for $\alpha =1,\ldots , N.$ We define the branches

$$\begin{aligned} J_{\alpha }= & {} [0,\infty ).e_{\alpha },\qquad J_{\alpha }^{\star } =J_{\alpha }{\setminus } \{0\}, \qquad \alpha =1,\ldots N,\\ J= & {} \bigcup _{\alpha =1,\ldots ,N} J_\alpha \quad \text { with } \quad J_{\alpha }\cap J_{\beta } =\{0\} \quad \text {for} \quad \alpha \ne \beta \end{aligned}$$

where the origin 0 is called the junction point.

Let $T>0$ be fixed and finite. For points $x,y\in J$, d(x, y) denotes the geodesic distance on J defined as

$$\begin{aligned} d(x,y)=\left\{ \begin{array}{ll} |x-y| &{}\quad \text { if } x,y \text { belong to the same branch},\\ |x|+|y| &{}\quad \text { if } x,y \text { belong to different branches.} \end{array}\right. \end{aligned}$$

With such a notation in hand, we consider the following Hamilton–Jacobi equation posed on the junction J,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} u_t+H_{\alpha }(u_x)=0 &{}\quad \text { in } (0,T)\times J_\alpha ^{\star }, \quad \alpha = 1, \dots , N \\ u_t +F\left( \frac{\partial u}{\partial x_{1}},\dots ,\frac{\partial u}{\partial x_{N}}\right) =0 &{}\quad \text { in } (0,T)\times \{0\}, \end{array}\right. \end{aligned}$$

(1.1)

with the initial condition

$$\begin{aligned} u(0,x)=u_0(x), \quad \text { for } x\in J \end{aligned}$$

(1.2)

where $u_0$ is globally Lipschitz in J. The second equation in (1.1) is referred to as the junction condition.

Hypotheses on the Hamiltonians We consider two cases of quasi-convex Hamiltonians $H_{\alpha }$. The first case is used for the theorem of convergence (Theorem 1.22) and here the Hamiltonians $H_{\alpha }$ satisfy the following conditions

$$\begin{aligned} \text {There exists}\ p_0^{\alpha } \in \mathbb {R}\ \text {such that } \left\{ \begin{array}{ll} H_{\alpha }\in C^1 (\mathbb {R}) \\ \pm H'_\alpha (p) \ge 0 \text { for } \pm (p-p_0^{\alpha }) \ge 0 \\ \lim _{|p|\rightarrow +\,\infty }H_{\alpha }(p)=+\,\infty . \end{array}\right. \end{aligned}$$

(1.3)

The second case is used for the error estimates (Theorem 1.2) and here the Hamiltonians $H_{\alpha }$ satisfy the following conditions

$$\begin{aligned} \text {There exists}\ p_0^{\alpha } \in \mathbb {R}\ \text {such that } \left\{ \begin{array}{ll} H_{\alpha }\in C^2 (\mathbb {R}) \text { and } H''_\alpha (p_0^{\alpha })>0 \\ \pm H'_\alpha (p)> 0 \text { for } \pm (p-p_0^{\alpha }) > 0 \\ \lim _{|p|\rightarrow +\,\infty }H_{\alpha }(p)=+\,\infty . \end{array}\right. \end{aligned}$$

(1.4)

In particular $H_{\alpha }$ is non-increasing in $(-\infty ,p_0^{\alpha }]$ and non-decreasing in $[p_0^{\alpha },+\,\infty )$, and we set

$$\begin{aligned} H_{\alpha }^-(p)={\left\{ \begin{array}{ll} H_{\alpha }(p) &{} \text { for } p \le p_0^{\alpha }\\ H_{\alpha }(p_0^{\alpha }) &{} \text { for } p\ge p_0^{\alpha } \end{array}\right. } \quad \text { and } \quad H_{\alpha }^+(p)= {\left\{ \begin{array}{ll} H_{\alpha }(p_0^{\alpha }) &{} \text { for } p \le p_0^{\alpha },\\ H_{\alpha }(p) &{} \text { for } p\ge p_0^{\alpha } \end{array}\right. } \end{aligned}$$

where $H_{\alpha }^-$ is non-increasing and $H_{\alpha }^+$ is non-decreasing.

Junction conditions We next introduce a one-parameter family of junction conditions: given a flux limiter$A\in \mathbb {R}\cup \{-\infty \},$ the A-limited flux junction function is defined for $\mathbf {p}=(p_1,\dots ,p_N)$ as,

$$\begin{aligned} F_{A}(\mathbf {p})=\max \bigg (A,\max _{\begin{array}{c} \alpha =1,\dots ,N \end{array}} H_{\alpha }^{-}(p_{\alpha })\bigg ) \end{aligned}$$

(1.5)

for some given $A \in \mathbb {R}\bigcup \{-\infty \}$ where $H_{\alpha }^{-}$ is the non-increasing part of $H_{\alpha }$.

We now consider the following important special case of (1.1),

$$\begin{aligned} \left\{ \begin{array}{ll} u_t+H_{\alpha }(u_x)=0 &{} \text { in } (0,T)\times J_\alpha ^{\star }, \\ u_t +F_A\left( \frac{\partial u}{\partial x_{1}},\dots ,\frac{\partial u}{\partial x_{N}}\right) =0 &{} \text { in } (0,T)\times \{0\}. \end{array}\right. \end{aligned}$$

(1.6)

We point out that all the junction functions $F_A$ associated with $A\in [-\infty ,A_0]$ coincide if one chooses

$$\begin{aligned} A_0= \max _{\begin{array}{c} \alpha =1,\dots ,N \end{array}}\min _{\begin{array}{c} \mathbb {R} \end{array}} H_{\alpha } =\max _{\begin{array}{c} \alpha =1,\dots ,N \end{array}} H_{\alpha }(p_0^{\alpha }). \end{aligned}$$

(1.7)

As far as general junction conditions are concerned, we assume that the junction function $F:\mathbb {R}^{n}\mapsto \mathbb {R}$ satisfies

$$\begin{aligned} \left\{ \begin{array}{l} F\text { is continuous and piecewise } C^{1}(\mathbb {R}^N),\\ \forall \alpha , \forall \mathbf {p}=(p_1,\dots ,p_N) \in \mathbb {R}^{N}, \frac{\partial F}{\partial p_{\alpha }}(\mathbf {p})<0, \\ F (p_1,\dots ,p_N) \rightarrow + \infty \text { as } \displaystyle \min _{i\in \{1,\dots ,N\}} p_i \rightarrow -\infty . \end{array}\right. \end{aligned}$$

(1.8)

Hypothesis in the following of the paper:$p_{0}^{\alpha }=0$ Without loss of generality (see [25, Lemma 3.1]), we consider in this paper that $p_{0}^{\alpha }=0$ for $\alpha =1,\ldots ,N$, i.e.,

$$\begin{aligned} \min \limits _{\mathbb {R}} H_{\alpha }=H_{\alpha }(0). \end{aligned}$$

(1.9)

Indeed, u solves (1.6) if and only if $\tilde{u}(t, x) := u(t, x)-p_{0}^{\alpha }x$ for $x\in J_{\alpha }$ solves the same equation in which $H_{\alpha }$ is replaced by $\tilde{H}_{\alpha }(p)=H_{\alpha }(p+p_{0}^{\alpha })$. We have the same result for $u^{h}$ the solution of the scheme (1.16).

The optimal control framework It is well known that the Legendre-Fenchel conjugate is crucial in establishing a link between the general Cauchy problem (1.6)–(1.2) and a control problem [28]. Through this link, we obtain the representation formula for the exact solution. While deriving the error estimate, regarding to Lemma 6.2, treating the case where the Hamiltonians $H_{\alpha }$ satisfy (1.4), reduce to the case of Hamiltonians satisfying the hypotheses of [26] i.e.,

$$\begin{aligned} \left\{ \begin{array}{ll} (\mathbf{Regularity}) &{} H_{\alpha }\text { is of class } C^2 \\ (\mathbf{Coercivity}) &{} \lim _{|p|\rightarrow +\,\infty }H_{\alpha }(p) =+\,\infty \\ (\mathbf{Convexity}) &{}H_\alpha \text { is convex and is the Legendre Fenchel transform of } L_{\alpha } \\ &{}\text { where } L_{\alpha } \text { is of class } C^{2} \text { and satisfies (B0)}. \end{array}\right. \end{aligned}$$

(1.10)

We recall that

$$\begin{aligned} H_{\alpha }(p)=L_{\alpha }^{\star }(p)=\sup _{q\in \mathbb {R}} (pq-L_{\alpha }(q)). \end{aligned}$$

(1.11)

We consider the following hypothesis for $L_{\alpha }$,

$$\begin{aligned} \begin{array}{c} \mathbf (B0) \ \text {There exists a constant}\ \gamma>0\ \text {such that for all} \ \alpha =1,\ldots ,N,\ \text {the}\ C^2(\mathbb {R})\ \\ \text {functions}\ L_{\alpha } \text {satisfy}\ L_{\alpha }^{\prime \prime }\ge \gamma >0. \end{array} \end{aligned}$$

An optimal control interpretation of the Hamilton–Jacobi equation (1.6) is given in [4, 7, 27, 28]. Let $(e_{\alpha })_{\alpha =1,\dots ,N}$ be the family of unit vectors for each $J_{\alpha }$. We define the set of admissible controls at a point $x\in J$ by

$$\begin{aligned} \mathcal {U}(x)=\left\{ \begin{array}{ll} \mathbb {R}e_{\alpha _{0}} &{}\text { if } x\in J_{\alpha _{0}}^{\star },\\ \cup _{\alpha =1,\ldots N}\mathbb {R}^{+} e_{\alpha } &{}\text { if } x=0. \end{array}\right. \end{aligned}$$

For $(s,y), (t,x)\in [0,T]\times J$ with $s\le t,$ we define the set of admissible trajectories from (s, y) to (t, x) by

$$\begin{aligned} \mathcal {A}(s ,y;t,x)=\left\{ X\in W^{1,1}([s,t], \mathbb {R}^2): \quad \left| \begin{array}{ll} X(\tau )\in J &{} \text { for all } \tau \in (s,t)\\ \dot{X} (\tau ) \in \mathcal {U}(X(\tau )) &{} \text { for a.e } \tau \in (s,t)\\ X(s)=y &{} \text { and } X(t)=x \end{array}\right| \right\} . \end{aligned}$$

(1.12)

For $P=pe_i\in \mathcal {U}(x)$ with $p\in \mathbb {R},$ we define the Lagrangian on the junction

$$\begin{aligned} L(x,P)=\left\{ \begin{array}{ll} L_{\alpha }(p) &{} \text { if } x\in J_{\alpha }^{\star },\\ \tilde{L}_{A}(p) &{} \text { if } x=0, \end{array}\right. \end{aligned}$$

(1.13)

with

$$\begin{aligned} \tilde{L}_{A}(p)= \min \bigg (-A,\min _{\begin{array}{c} \alpha =1,\dots ,N \end{array}} L_{\alpha }(p)\bigg ). \end{aligned}$$

The Hopf-Lax representation formula provides a solution of (1.6)–(1.2) only assuming (1.10). This formula is given in [2, 26] by

$$\begin{aligned} u_{oc}(t,x)= \inf _{\begin{array}{c} {y\in J} \end{array}}\{u_0(y)+\mathcal {D}(0,y;t,x)\} \end{aligned}$$

(1.14)

with

$$\begin{aligned} \mathcal {D}(s,y;t,x)=\inf _{\begin{array}{c} {X\in \mathcal {A}(s,y;t,x)} \end{array}}\bigg \{\int _s^t L(X(\tau ),\dot{X}(\tau ))d\tau \bigg \}. \end{aligned}$$

Remark 1

More details about this function are explained in Sect. 5 where the relevant trajectories of the optimal control problem are given. Also this function plays a crucial role in getting the error estimates with the doubling variable method.

1.2 Presentation of the scheme

The domain $(0,+\,\infty ) \times J$ is discretized with respect to time and space with a constant time step and space step. The space step is denoted by $\Delta x$ and the time step by $\Delta t$. If h denotes $(\Delta t,\Delta x)$, the mesh (or grid) $\mathcal {G}_h$ is chosen as

$$\begin{aligned} \mathcal {G}_h = \{n \Delta t : n \in \mathbb {N}\} \times J^{\Delta x} \end{aligned}$$

(1.15)

where

$$\begin{aligned} J^{\Delta x} = \bigcup _{\alpha =1,\dots ,N} J_\alpha ^{\Delta x} \quad \text { with } \quad J_\alpha \supset J_\alpha ^{\Delta x} \simeq \{ i \Delta x : i \in \mathbb {N}\}\cdot e_{\alpha } . \end{aligned}$$

It is convenient to write $x_i^{\alpha }$ for $i\Delta x \in J_\alpha$.

A numerical approximation $u^h$ of the solution u of the Hamilton–Jacobi equation (1.1) is defined in $\mathcal {G}_h$; the quantity $u^h (n \Delta t, x_i^{\alpha })$ is simply denoted by $U_i^{\alpha , n}$. We want it to be an approximation of $u(n\Delta t, x_i^{\alpha })$ for $n \in \mathbb {N}$, $i\in \mathbb {N}$, where $\alpha$ stands for the index of the branch.

We consider the following time-explicit scheme: for $n\ge 0$,

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{U^{\alpha ,n+1}_i-U^{\alpha ,n}_i}{\Delta t} +\max \{H_{\alpha }^{+}(p_{i,-}^{\alpha ,n}),H_{\alpha }^{-} (p_{i,+}^{\alpha ,n})\}=0, &{}\quad i\ge 1, &{} \alpha =1,\dots ,N\\ U_0^{\beta ,n}:=U_0^n, &{}\quad i=0, &{} \beta =1,\dots ,N\\ \frac{U_0^{n+1}-U_0^{n}}{\Delta t}+F(p_{0,+}^{1,n}, \dots ,p_{0,+}^{N,n})=0, &{} &{} \end{array}\right. \end{aligned}$$

(1.16)

where $p_{i,\pm }^{\alpha ,n}$ are the discrete (space) gradients defined by

$$\begin{aligned} p_{i,+}^{\alpha ,n}:= \frac{U_{i+1}^{\alpha ,n} -{U_{i}^{\alpha ,n}}}{\Delta x}, \qquad p_{i,-}^{\alpha ,n}:= \frac{U_{i}^{\alpha ,n} -{U_{i-1}^{\alpha ,n}}}{\Delta x} \end{aligned}$$

(1.17)

with the initial condition

$$\begin{aligned} U_i^{\alpha ,0}=u_0(x_i^{\alpha }), \quad i\ge 0,\quad \alpha =1,\dots ,N. \end{aligned}$$

(1.18)

One can notice that $p_{i,-}^{\alpha ,n}=p_{i-1,+}^{\alpha ,n}$ but the notation is useful to do the analogy between the viscosity inequalities in the discrete (see Lemma 4.3) and continuous case (see Proposition 2.4).

The following Courant–Friedrichs–Lewy (CFL) condition ensures that the explicit scheme is monotone (proof provided in Lemma 4.1),

$$\begin{aligned} \frac{\Delta x}{\Delta t}\ge \max \bigg \{ \max _{\begin{array}{c} {i\ge 0},\\ {\alpha =1,\dots ,N,}\\ {0\le n\le n_T} \end{array}} {|H_{\alpha }^{'}(p_{i,+}^{\alpha ,n})|}; \max _{\begin{array}{c} 0\le n\le n_T \end{array}}\bigg \{(-\nabla \cdot F) (p_{0,+}^{1,n},\dots ,p_{0,+}^{N,n})\bigg \}\bigg \} \end{aligned}$$

(1.19)

where the integer $n_T$ is the integer part of $\frac{T}{\Delta t}$ for a given $T>0$.

1.3 Main results

As previously noticed in [16] in the special case $F=F_{A_0}$, it is not clear that the time step $\Delta t$ and space step $\Delta x$ can be chosen in such a way that the CFL condition (1.19) holds true since the discrete gradients $p_{i,+}^{\alpha ,n}$ depend itself on $\Delta t$ and $\Delta x$ (through the numerical scheme). We thus impose a more stringent CFL condition,

$$\begin{aligned} \frac{\Delta x}{\Delta t}\ge \max \bigg \{\max _{\begin{array}{c} {\alpha =1,\dots ,N},\\ {\underline{p}_{\alpha }\le p\le \overline{p}_\alpha } \end{array}}{|H_{\alpha }'(p)|}; \max _{\begin{array}{c} {\alpha =1,\dots ,N},\\ \underline{p}_{\alpha }^0\le p_{\alpha } \le \overline{p}_\alpha \end{array}} \bigg \{(-\nabla \cdot F)(p_{1}, \dots ,p_{N})\bigg \}\bigg \} \end{aligned}$$

(1.20)

for some $\underline{p}_\alpha ,\overline{p}_\alpha , \underline{p}_\alpha ^0 \in \mathbb {R}$ to be fixed (only depending on $u_0$, H, and F). We can argue as in [16] and prove that $\underline{p}_\alpha ,\overline{p}_\alpha ,\underline{p}_\alpha ^0 \in \mathbb {R}$ can be chosen in such a way that the CFL condition (1.20) implies (1.19) and, in turn, the scheme is monotone (Lemma 4.1 in Sect. 4). We will also see that it is stable (Lemma 4.4) and consistent (Lemma 4.5). It is thus known that it converges [6, 17]. Notice that taking $F=F_{A}$, gives the following CFL condition

$$\begin{aligned} \frac{\Delta x}{\Delta t}\ge \max _{\begin{array}{c} {\alpha =1,\dots ,N},\\ {\underline{p}_{\alpha }\le p\le \overline{p}_\alpha } \end{array}} {|H_{\alpha }'(p)|}. \end{aligned}$$

(1.21)

Theorem 1.1

(Convergence for general junction conditions) Let $T>0$ and $u_0$ be Lipschitz continuous. Let the Hamiltonians $H_{\alpha }$ satisfy (1.3) and the junction function F satisfies (1.8). Then there exist $\underline{p}_\alpha , \overline{p}_\alpha ,\underline{p}_\alpha ^0 \in \mathbb {R}$, $\alpha =1,\dots , N$, depending only on the initial data,$H_{\alpha }$ and F such that, if h satisfies the CFL condition (1.20), then the numerical solution $u^h$ defined by (1.16)–(1.18) converges locally uniformly as h goes to zero to the unique relaxed viscosity solution u of (1.1)–(1.2), on any compact set $\mathcal {K} \subset [0, T )\times J$, i.e.

$$\begin{aligned} \limsup _{|h| \rightarrow 0} \sup _{\begin{array}{c} (t,x)\in \mathcal {K} \cap \mathcal {G}_h \end{array}}|u^h (t,x)-u(t,x)|=0, \end{aligned}$$

(1.22)

where $h=(\Delta t, \Delta x)$.

Remark 2

We know from [25] that the equation (1.1)–(1.2) may have no viscosity solution but always a unique relaxed viscosity solution (in the sense of Definition 2). Notice that the scheme has a junction condition which is not relaxed. However the solution of the scheme converges to the unique relaxed solution of the associated Hamilton–Jacobi equation.

The main result of this paper lies in getting error estimates in the case of flux-limited junction conditions.

Theorem 1.2

(Error estimates for flux-limited junction conditions) Let $T>0$ and $u_0$ be Lipschitz continuous. Let the Hamiltonians $H_{\alpha }$ satisfy (1.4), $u^h$ be the solution of the associated numerical scheme (1.16)–(1.18) and u be the viscosity solution of (1.6)–(1.2) for some $A \in \mathbb {R}$. If the CFL condition (1.21) is satisfied, then there exists $C>0$ (independent of h) such that

$$\begin{aligned} \sup _{\begin{array}{c} [0,T)\times J \cap \mathcal {G}_h \end{array}} |u^h(t,x)-u(t,x)|\le {\left\{ \begin{array}{ll} C(\Delta x)^{1/2} &{} \text { if } A > A_0, \\ C (\Delta x)^{2/5} &{} \text { if } A = A_0. \end{array}\right. } \end{aligned}$$

(1.23)

1.4 Related results

Numerical schemes for Hamilton–Jacobi equations on networks The discretization of viscosity solutions of Hamilton–Jacobi equations posed on networks has been studied in a few papers only. Apart from [16] mentioned above, we are only aware of two other works. A convergent semi-Lagrangian scheme is introduced in [9] for equations of eikonal type and in [13] for Hamilton–Jacobi equations with application to traffic flow models. In [23], an adapted Lax-Friedrichs scheme is used to solve a traffic model; it is worth mentioning that this discretization implies to pass from the scalar conservation law to the associated Hamilton–Jacobi equation at each time step.

Numerical schemes for Hamilton–Jacobi equations for optimal control problems For optimal control problems, the numerical approximation of Hamilton–Jacobi equations has already been studied using schemes based on the discrete dynamic programming principle. Essentially, these schemes are built by replacing the continuous optimal control problem by its discrete time version. We refer to Capuzzo Dolcetta [11], Capuzzo Dolcetta-Ishii [12] for the results concerning the convergence of $u_h$ to u and the a priori estimates (of order $\Delta x)$ , in the $L^{\infty }$ norm, giving the order of convergence of the discrete-time approximation. For papers related to Lax-Hopf formulas and programming principle with a traffic application, we refer to [8]. We refer to Falcone [20] for the results related to the order of convergence of the fully discrete (i.e. in space and time) approximation and for the construction of the algorithm, we mention that under a semiconcavity assumption the rate of convergence is of order 1. We cite also [21] and references therein for discrete time high order schemes for Hamilton Jacobi Bellman equations. Also semi-Lagrangian schemes [9] can be seen as a discrete version of the Hopf-Lax formula and are related to optimal control problems.

Link with monotone schemes for scalar conservation laws We first follow [16] by emphasizing that the convergence result, Theorem 1.1, implies the convergence of a monotone scheme for scalar conservation laws (in the sense of distributions).

In order to introduce the scheme, it is useful to introduce a notation for the numerical Hamiltonian $\mathcal {H}_\alpha$,

$$\begin{aligned} \mathcal {H}_\alpha (p^+,p^-) =\max \{H_{\alpha }^{-}(p^+),H_{\alpha }^{+}(p^-)\}. \end{aligned}$$

The discrete solution $(V^n)$ of the scalar conservation law $v_t+(H_{\alpha }(v))_x=0$ with $v=u_x$ far from the junction is defined as follows,

$$\begin{aligned} V ^{\alpha ,n}_{i+\frac{1}{2}}={\left\{ \begin{array}{ll} \frac{U^{\alpha ,n}_{i+1}-U^{\alpha ,n}_i}{\Delta x} &{} \text { if } i \ge 1 \\ \frac{U^{\alpha ,n}_1 -U^n_0}{\Delta x} &{} \text { if } i = 0. \end{array}\right. } \end{aligned}$$

In view of (1.16), it satisfies for all $\alpha =1,\dots ,N$,

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{V^{\alpha ,n+1}_{i+\frac{1}{2}}-V^{\alpha ,n}_{i+\frac{1}{2}}}{\Delta t} + (\Delta x)^{-1} \left( \mathcal {H}_\alpha \left( V^{\alpha ,n}_{i+\frac{3}{2}},V^{\alpha ,n}_{i+\frac{1}{2}}\right) -\mathcal {H}_\alpha \left( V^{\alpha ,n}_{i+\frac{1}{2}}, V^{\alpha ,n}_{i-\frac{1}{2}}\right) \right) =0, &{} i\ge 1, \\ \frac{V_{\frac{1}{2}}^{\alpha ,n+1}-V_{\frac{1}{2}}^{\alpha ,n}}{\Delta t} + (\Delta x)^{-1} \left( \mathcal {H}_\alpha \left( V^{\alpha ,n}_{\frac{3}{2}},V^{\alpha ,n}_{\frac{1}{2}}\right) - F\left( V_{\frac{1}{2}}^{1,n},\dots ,V_{\frac{1}{2}}^{N,n}\right) \right) =0, &{} \end{array}\right. \end{aligned}$$

submitted to the initial condition

$$\begin{aligned} V_{i+\frac{1}{2}}^{\alpha ,0}=\frac{u_0(x_i^{\alpha })-u_0(0)}{\Delta x}, \quad i\ge 0,\quad \alpha =1,\dots ,N. \end{aligned}$$

In view of Theorem 1.1, we thus can conclude that the discrete solution $v^h$ constructed from $(V^n)$ converges towards $u_x$ in the sense of distributions, at least far from the junction point.

Error estimates for numerical schemes We would like next to explain why our result can be seen as the Hamilton–Jacobi counterpart of the error estimates obtained by Ohlberger and Vovelle [29] for scalar conservation laws submitted to Dirichlet boundary conditions.

On the one hand, it is known since 1979 and Bardos et al. [5] that Dirichlet boundary conditions imposed to scalar conservation laws should be understood in a generalized sense. This can be seen by studying the parabolic regularization of the problem. A boundary layer analysis can be performed for systems if the solution of the conservation law is smooth; see for instance [22, 24]. Depending on the fact that the boundary is characteristic or not, the error is $h^{\frac{1}{2}}$ or h. In the scalar case, it is proved in [19] that the error between the solution of the regularized equation with a vanishing viscosity coefficient equal to h and the entropy solution of the conservation law (which is merely of bounded variation in space) is of order $h^{1/3}$ (in $L^{\infty }_t L^1_x$ norm). In [29], the authors derive error estimates for finite volume schemes associated with such boundary value problems and prove that it is of order $(\Delta x)^{1/6}$ (in $L^1_t L^1_x$ norm). More recently, scalar conservation laws with flux constraints were studied [14, 15] and some finite volume schemes were built [3]. In [10], assuming that the flux is bell-shaped, that is to say the opposite is quasi-convex, it is proved that the error between the finite volume scheme and the entropy solution is of order $(\Delta x)^{\frac{1}{3}}$ and that it can be improved to $(\Delta x)^{\frac{1}{2}}$ under an additional condition on the traces of the BV entropy solution. It is not known if the estimates from [10] are optimal or not.

On the other hand, the derivative of a viscosity solution of a Hamilton–Jacobi equation posed on the real line is known to coincide with the entropy solution of the corresponding scalar conservation law. It is therefore reasonable to expect that the error between the viscosity solution of the Hamilton–Jacobi equation and its approximation is as good as the one obtained between the entropy solution of the scalar conservation law and its approximation.

Moreover, it is explained in [26] that the junction conditions of optimal-control type are related to the Bardos, Le Roux and Nédélec (BLN) condition mentioned above. It is therefore interesting to get an error estimate of order $(\Delta x)^{1/2}$ for the Hamilton–Jacobi problem.

1.5 Open problems

Let us first mention that it is not known if the error estimate between the (entropy) solution of the scalar conservation law with Dirichlet boundary condition and the solution of the parabolic approximation [19] or with the numerical scheme [29] is optimal or not. Here, we prove an optimal error estimate for $A>A_{0}$ but we do not know if our error estimate is optimal or not for $A=A_{0}$. But the test performed seems to suggest that the estimate is not optimal for $A=A_0$.

Deriving error estimates for general junction conditions seems difficult to us. The main difficulty is the singular geometry of the domain. The test function, used in deducing the error estimates with flux limited solutions, is designed to compare flux limited solutions. Consequently, when applying the reasoning of Sect. 6, the discrete viscosity inequality cannot be combined with the continuous one.

1.6 Organization of the article

The remaining of the paper is organized as follows. In Sect. 2, we recall definitions and results from [25] about viscosity solutions for (1.1)–(1.2). Section 3 is dedicated to the derivation of discrete gradient estimates for the numerical scheme. In Sect. 4, the convergence result, Theorem 1.1 is proved. In Sect. 5, we study the reduced minimal action for a “strictly” limited flux and prove that the gradient is locally Lipschitz continuous (at least if the flux is strictly limited). The final section, Sect. 6, is dedicated to the proof of the error estimates.

2 Preliminaries

2.1 Viscosity solutions

We introduce the main definitions related to viscosity solutions for Hamilton–Jacobi equations that are used in the remaining. For a more general introduction to viscosity solutions, the reader could refer to Barles [7] and to Crandall et al. [18].

Space of test functions For a smooth real valued function u defined on J, we denote by $u^{\alpha }$ the restriction of u to $(0,T)\times J_{\alpha }$. Let $J_T= (0,T)\times J$.

Then we define the natural space of functions on the junction:

$$\begin{aligned} C^1(J_T)=\{u \in C(J_T) : \forall \alpha =1,\dots ,N, u^{\alpha } \in C^1((0,T)\times J_\alpha )\}. \end{aligned}$$

Viscosity solutions In order to define classical viscosity solutions, we recall the definition of upper and lower semi-continuous envelopes $u^{\star }$ and $u_{\star }$ of a (locally bounded) function u defined on $[0, T ) \times J$:

$$\begin{aligned} u^{\star }(t,x)=\limsup _{(s,y)\rightarrow (t,x)}u(s,y)\qquad u_{\star }(t,x)=\liminf _{(s,y)\rightarrow (t,x)}u(s,y). \end{aligned}$$

Definition 1

(Viscosity solution) Assume that the Hamiltonians satisfy (1.4) and that F satisfies (1.8) and let $u :(0,T)\times J \rightarrow \mathbb {R}.$

• (i) We say that u is a sub-solution (resp. super-solution) of (1.1) in $(0,T)\times J$ if for all test function $\varphi \in C^{1}(J_{T})$ such that

  $$\begin{aligned} u^{\star }\le \varphi \quad (\text {resp. } u_{\star }\ge \varphi ) \quad \text { in a neighborhood of } \quad (t_0,x_0)\in J_{T} \end{aligned}$$

  with equality at $(t_0,x_0)$ for some $t_{0}>0,$ we have

  $$\begin{aligned} \left\{ \begin{array}{lll} \varphi _{t}+H_{\alpha }(\varphi _{x})\le 0 &{} \quad (\text {resp. } \ge 0) &{} \quad \text { at } (t_{0},x_{0})\in (0,T)\times J_{\alpha }^{\star } \\ \varphi _{t}+F_A\left( \frac{\partial \varphi }{\partial _{x_1}},\dots , \frac{\partial \varphi }{\partial _{x_N}}\right) \le 0 &{}\quad (\text {resp. }\ge 0) &{} \quad \text { at } (t_{0},x_{0})\in (0,T)\times \{0\}. \end{array}\right. \end{aligned}$$

• (ii) We say that u is a sub-solution (resp. super-solution) of (1.1)-(1.2) on $[0,T)\times J$ if additionally

  $$\begin{aligned} u^{\star }(0,x)\le u_{0}(x) \quad (\text {resp. } u_{\star }(0,x)\ge u_{0}(x)) \quad \text { for all} \quad x\in J. \end{aligned}$$

• (iii) We say that u is a (viscosity) solution if u is both a sub-solution and a super-solution.

As explained in [25], it is difficult to construct viscosity solutions in the sense of Definition 1 because of the junction condition. It is possible in the case of the flux-limited junction conditions $F_A$. For general junction conditions, the Perron process generates a viscosity solution from the following relaxed sense [25].

Definition 2

(Relaxed viscosity solution) Assume that the Hamiltonians satisfy (1.4) and that F satisfies (1.8) and let $u :(0,T)\times J\rightarrow \mathbb {R}.$

• (i) We say that u is a relaxed sub-solution (resp. relaxed super-solution) of (1.1) in $(0,T)\times J$ if for all test function $\varphi \in C^{1}(J_T)$ such that

  $$\begin{aligned} u^{\star } \le \varphi \quad (\text {resp. } u_{\star } \ge \varphi ) \quad \text { in a neighborhood of } \quad (t_0,x_0)\in J_{T} \end{aligned}$$

  with equality at $(t_0,x_0)$ for some $t_{0}>0,$ we have if $x_0 \ne 0$

  $$\begin{aligned} \varphi _{t}+H_{\alpha }(\varphi _{x})\le 0\qquad (\text {resp.}\quad \ge 0) \quad \text { at } \quad (t_{0},x_{0})\in (0,T)\times J_{\alpha }^{\star }, \end{aligned}$$

  if $x_0 =0$,

  $$\begin{aligned} {\left\{ \begin{array}{ll} \text {either } \quad \varphi _{t}+F\left( \frac{\partial \varphi }{\partial x_1}, \dots , \frac{\partial \varphi }{\partial x_N}\right) \le 0 \quad (\text {resp. } \ge 0) &{} \text { at } (t_{0},x_{0})=(t_0,0)\\ \text {or } \quad \varphi _{t}+H_{\alpha } \left( \frac{\partial \varphi }{\partial x_\alpha }\right) \le 0 \quad (\text {resp. } \ge 0) &{} \text { at } (t_{0},x_{0})=(t_0,0) \quad \text { for some } \alpha . \end{array}\right. } \end{aligned}$$

• (ii) We say that u is a relaxed (viscosity) solution of (1.1) if u is both a relaxed sub-solution and a super-solution.

Let us recall some theorems in [25].

Theorem 2.1

(Comparison principle on a junction) Let $A\in \mathbb {R}\cup \{-\infty \}$. Assume that the Hamiltonians satisfy (1.3) and the initial datum $u_0$ is uniformly continuous. Then for all sub-solution u and super-solution v of (1.6)–(1.2) satisfying for some $T>0$ and $C_T>0$

$$\begin{aligned}&u(t,x)\le C_{T}(1+d(0,x)), \quad v(t,x)\ge -C_{T}(1+d(0,x)),\\&\quad \text { for all} \quad (t,x)\in [0,T)\times J, \end{aligned}$$

we have

$$\begin{aligned} u\le v \quad in\quad [0,T)\times J. \end{aligned}$$

Theorem 2.2

(General junction conditions reduce to flux-limited ones) Assume that the Hamiltonians satisfy (1.3) and that F satisfies (1.8). Then there exists $A_F\in \mathbb {R}$ such that any relaxed viscosity (sub-/super-)solution of (1.1) is in fact a viscosity (sub-/super-)solution of (1.6) with $A=A_F.$

Theorem 2.3

(Existence and uniqueness on a junction) Assume that the Hamiltonians satisfy (1.3) and that F satisfies (1.8) and that the initial datum $u_0$ is Lipschitz continuous. Then there exists a unique relaxed viscosity solution u of (1.1)–(1.2), such that

$$\begin{aligned} |u(t,x)-u_{0}(x)|\le C t \quad \text { for all } \quad (t,x)\in [0,T)\times J \end{aligned}$$

for some constant C only depending on H and $u_0$. Moreover, it is Lipschitz continuous with respect to time and space, in particular,

$$\begin{aligned} \Vert \nabla u \Vert _\infty \le C. \end{aligned}$$

The following proposition is a main tool in the proof of error estimates. Indeed, we use a test function which is not $C^{1}$ with respect to the gradient variable at one point and this proposition allows us to get a “weak viscosity inequality”. We don’t give the proof since it is the same as the proof of [25, Proposition 2.16].

Proposition 2.4

(Non $C^{1}$ test function at one point [25]) that H satisfies (1.3) and let u be a solution of

$$\begin{aligned} u_t+H_{\alpha }(u_x)=0 \quad \text { in } (0,T)\times J_\alpha ^{\star }. \end{aligned}$$

For all $x_{0}\in J_\alpha ^{\star }$ and all test function $\varphi \in C^{1}((0,T)\times J_\alpha {\setminus } \{0,x_{0}\})$

$$\begin{aligned} u^{\star }\le \varphi \quad (\text {resp. } u_{\star }\ge \varphi ) \quad \text { in a neighborhood of } \quad (t_0,x_{0})\in (0,T) \times J_\alpha ^{\star } \end{aligned}$$

with equality at $(t_0,x_{0})$, we have

$$\begin{aligned} \varphi _{t}(t_{0},x_{0})+\max \left\{ H_{\alpha }^{+}(\varphi _{x} (t_{0},x_{0}^{-}),H_{\alpha }^{-}(\varphi _{x}(t_{0},x_{0}^{+})\right\} \le 0 \quad (\text {resp. } \ge 0). \end{aligned}$$

3 Discrete gradient estimates

This section is devoted to the proofs of the discrete (time and space) gradient estimates. These estimates ensure the monotonicity of the scheme and, in turn, its convergence. The discrete time derivative is defined as

$$\begin{aligned} W_i^{\alpha ,n}:=\frac{U_i^{\alpha ,n+1}-U_i^{\alpha ,n}}{\Delta t}. \end{aligned}$$

Theorem 3.1

(Discrete gradient estimates) If $u^h=(U_i^{\alpha ,n})$ is the numerical solution of (1.16)–(1.18) and if the CFL condition (1.20) is satisfied and if

$$\begin{aligned} m^0= \inf _{\begin{array}{c} \beta =1,\dots ,N,\\ i \in \mathbb {N} \end{array} }W_i^{\beta ,0} \end{aligned}$$

(3.1)

is finite, then the following two properties hold true for any $n\ge 0$.

• (i) (Gradient estimate) There exist $\underline{p}_{\alpha }$,$\overline{p}^{\alpha }$, $\underline{p}^0_{\alpha }$ (only depending on $H_\alpha$, $u_0$ and F) such that

  $$\begin{aligned} \left\{ \begin{array}{l} \underline{p}_{\alpha }\le p_{i,+}^{\alpha ,n}\le \overline{p}^{\alpha } \qquad i\ge 1, \; \alpha =1,\dots ,N, \\ \underline{p}_{\alpha }^0\le p_{0,+}^{\alpha ,n}\le \overline{p}^{\alpha }\qquad i= 0, \; \alpha =1,\dots ,N. \end{array}\right. \end{aligned}$$

  (3.2)

• (ii) (Time derivative estimate) The discrete time derivative $W_i^{\alpha ,n}$ satisfies

  $$\begin{aligned} m^0\le m^n\le m^{n+1}\le M^{n+1}\le M^n\le M^0 \end{aligned}$$

  where

  $$\begin{aligned} m^n :=\inf _{\alpha , i} W_{i}^{\alpha , n}, \qquad M^n :=\sup _{\alpha , i} W_{i}^{\alpha , n}. \end{aligned}$$

In the proofs of discrete gradient estimates, “generalized” inverse functions of $H_{\alpha }^{\pm }$ are needed; they are defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \pi _\alpha ^+ (a):=\sup \{ p : H_{\alpha }^+ (p) = \max (a, A_{\alpha }) \} \\ \pi _\alpha ^- (a):=\inf \{ p : H_{\alpha }^- (p) = \max (a,A_{\alpha }) \} \end{array}\right. } \end{aligned}$$

(3.3)

with the additional convention that $(H_{\alpha }^{\pm })^{-1}(+\,\infty )=\pm \infty$, where

$$\begin{aligned} A_{\alpha }:=\min _{\begin{array}{c} \mathbb {R} \end{array}} H_{\alpha }. \end{aligned}$$

In order to define a “generalized” inverse function of F, we remark that (1.8) implies that

$$\begin{aligned} \begin{array}{c} \text { for all } K \in \mathbb {R}, \text { there exists } \underline{\rho }(K)=(\rho _{1}(K),\dots ,\rho _{N}(K)) \in \mathbb {R}^N \\ \text { such that } F(p_1,\dots ,p_N)\le K \Rightarrow p_{\alpha }\ge \underline{\rho }_{\alpha }(K). \end{array} \end{aligned}$$

Remark that the functions $\underline{\rho }_\alpha$ can be chosen non-increasing.

Remark 3

The quantities $\underline{p}_{\alpha }$,$\overline{p}^{\alpha }$, $\underline{p}^0_{\alpha }$ are defined as follows

$$\begin{aligned} \left\{ \begin{array}{l} \underline{p}_{\alpha }= \left\{ \begin{array}{ll} \pi _\alpha ^-(-m^0) &{} \text {if}-m^{0}>A_{\alpha }\\ \pi _\alpha ^-(-m^0+1) &{} \text {if}-m^{0}=A_{\alpha } \end{array}\right. \\ \overline{p}_{\alpha }= \left\{ \begin{array}{ll} \pi _\alpha ^+(-m^0) &{} \text {if}-m^{0}>A_{\alpha }\\ \pi _\alpha ^+(-m^0+1) &{} \text {if}-m^{0}=A_{\alpha } \end{array}\right. \\ \underline{p}^0_\alpha = \left\{ \begin{array}{ll} \underline{\rho }_\alpha (-m^0) &{} \text { if } \underline{\rho }_\alpha (-m^0)<\overline{p}_\alpha \\ \underline{\rho }_\alpha (-m^0+1) &{} \text { if } \underline{\rho }_\alpha (-m^0)=\overline{p}_\alpha \end{array}\right. \end{array}\right. \end{aligned}$$

(3.4)

where $m^0$ is defined in (3.1).

In order to establish Theorem 3.1, we first prove two auxiliary results. In order to state them, some notations should be introduced.

3.1 Discrete time derivative estimates

In order to state the first one, Proposition 3.2 below, we introduce some notation. For $\sigma \in \{+,-\}$, we set

$$\begin{aligned} I_{i,\sigma }^{\alpha , n}:= [\min (p_{i,\sigma }^{\alpha ,n}, p_{i,\sigma }^{\alpha ,n+1}), \max (p_{i,\sigma }^{\alpha ,n},p_{i,\sigma }^{\alpha ,n+1})] \end{aligned}$$

with $p_{i,\sigma }^{\alpha ,n}$ defined in (1.17) and

$$\begin{aligned} D_{i,+}^{\alpha ,n}:=\sup \bigg \{\sup _{p_{\alpha }\in I_{i,+}^{\alpha ,n}}|H'_{\alpha }(p_{\alpha })|, \sup _{p_{\alpha }\in I_{0,+}^{\alpha ,n}}\bigg \{-(\nabla \cdot F)(p_1,\dots ,p_N)\bigg \}\bigg \}. \end{aligned}$$

(3.5)

The following proposition asserts that if the discrete space gradients enjoy suitable estimates, then the discrete time derivative is controlled.

Proposition 3.2

(Discrete time derivative estimate) Let $n\ge 0$ be fixed and $\Delta x$, $\Delta t > 0.$ Let us consider $(U_{i,\alpha }^{\alpha ,n})_{\alpha ,i}$ satisfying for some constant $C^n >0$:

$$\begin{aligned} |p_{i,+}^{\alpha ,n}| \le C^n \qquad \text {for} \quad i\ge 0, \; \alpha =1,\dots ,N. \end{aligned}$$

We also consider $(U_{i}^{\alpha ,n+1})_{\alpha ,i}$ and $(U_{i}^{\alpha ,n+2})_{\alpha ,i}$ computed using the scheme (1.16). If

$$\begin{aligned} D_{i,+}^{\alpha ,n}\le \frac{\Delta x}{\Delta t} \qquad \text { for } \quad i\ge 0, \;\alpha =1,\dots ,N, \end{aligned}$$

(3.6)

then

$$\begin{aligned} m^n\le m^{n+1}\le M^{n+1}\le M^n. \end{aligned}$$

Proof

For $\sigma =+$ (resp. $\sigma =-$), $-\sigma$ denotes − (resp. $+$). We introduce for $n\ge 0,$$\alpha \in \{ 1,\dots ,N\}$, $i\in \{1,\dots ,N\}$, $\sigma \in \{+,-\}$,

$$\begin{aligned} C_{i,\sigma }^{\alpha ,n}&:=-\sigma \int _{0}^{1}(H^{-\sigma }_{\alpha })' \left( p_{i,\sigma }^{\alpha ,n+1}+\tau (p_{i,\sigma }^{\alpha ,n} -p_{i,\sigma }^{\alpha ,n+1})\right) d\tau \ge 0, \\ {C_{0,+}^{\alpha ,n}}&:=-\int _{0}^{1} \frac{\partial F}{\partial p_{\alpha }} \bigg (\{p_{0,+}^{\beta ,n+1}+\tau (p_{0,+}^{\beta ,n} -p_{0,+}^{\beta ,n+1})\}_{\beta }\bigg )d\tau \ge 0.\nonumber \end{aligned}$$

(3.7)

Notice that for $i\ge 1$, $C_{i,\sigma }^{\alpha ,n}$ is defined as the integral of $(H_{\alpha }^{-\sigma })'$ over a convex combination of $p\in I_{i,\sigma }^{\alpha ,n}.$ Similarly for $C_{0,+}^{\alpha ,n}$ which is defined as the integral of $F'$ on a convex combination of $p\in I_{0,+}^{\alpha ,n}.$ Hence, in view of (3.6), we have for any $n\ge 0$, $\alpha =1,\dots ,N$ and for any $\sigma \in \{+,-\}$ or for $i=0$ and $\sigma =+,$ we can check that

$$\begin{aligned} {\left\{ \begin{array}{ll} C_{i,\sigma }^{\alpha ,n}\le \frac{\Delta x}{\Delta t} &{} \text { if } i \ge 1, \, \sigma \in \{-,+\} \\ \sum _{\beta =1}^N C_{0,+}^{\beta ,n} \le \frac{\Delta x}{\Delta t}. &{} \end{array}\right. } \end{aligned}$$

(3.8)

We can also underline that for any $n\ge 0$, $\alpha =1,\dots ,N$ and for any $i\ge 1,$$\sigma \in \{+,-\}$ or for $i=0$ and $\sigma =+,$ we have the following relationship

$$\begin{aligned} \frac{p_{i,\sigma }^{\alpha ,n}-p_{i,\sigma }^{\alpha ,n+1}}{\Delta t}= -\sigma \frac{W_{i+\sigma }^{\alpha ,n}-W_{i}^{\alpha ,n}}{\Delta x}. \end{aligned}$$

(3.9)

Let $n\ge 0$ be fixed and consider $(U_i^{\alpha ,n})_{\alpha ,i}$ with $\Delta x,\Delta t>0$ given. We compute $(U_i^{\alpha ,n+1})_{\alpha ,i}$ and $(U_i^{\alpha ,n+2})_{\alpha ,i}$ using the scheme (1.16).

Step 1:$(m^n)_n$is non-decreasing We want to show that $W_i^{\alpha ,n+1}\ge m^n$ for $i\ge 0$ and $\alpha =1,\dots ,N.$ Let $i\ge 0$ be fixed and let us distinguish two cases.

Case 1:$i\ge 1$ Let a branch $\alpha$ be fixed and let $\sigma (i,\alpha ,n+1)=\sigma \in \{+,-\}$ be such that

$$\begin{aligned} \max \bigg \{H_{\alpha }^{+}(p_{i,-}^{\alpha ,n+1}), H_{\alpha }^{-}(p_{i,+}^{\alpha ,n+1})\bigg \} =H_{\alpha }^{-\sigma }(p_{i,\sigma }^{\alpha ,n+1}). \end{aligned}$$

(3.10)

We have

$$\begin{aligned} \frac{W_i^{\alpha ,n+1}-W_i^{\alpha ,n}}{\Delta t}= & {} \frac{1}{\Delta t}\bigg (\max \bigg \{H_{\alpha }^{+} (p_{i,-}^{\alpha ,n}),H_{\alpha }^{-}(p_{i,+}^{\alpha ,n})\bigg \}\\&-\max \bigg \{H_{\alpha }^{+}(p_{i,-}^{\alpha ,n+1}), H_{\alpha }^{-}(p_{i,+}^{\alpha ,n+1})\bigg \}\bigg )\\\ge & {} \frac{1}{\Delta t}\bigg (H_{\alpha }^{-\sigma } (p_{i,\sigma }^{\alpha ,n})- H_{\alpha }^{-\sigma } (p_{i,\sigma }^{\alpha ,n+1})\bigg )\\= & {} \int _{0}^{1}(H_{\alpha }^{-\sigma })'(p_{i,\sigma }^{\alpha ,n+1} +\tau (p_{i,\sigma }^{\alpha ,n}-p_{i,\sigma }^{\alpha ,n+1})) \left( \frac{p_{i,\sigma }^{\alpha ,n}-p_{i,\sigma }^{\alpha ,n+1}}{\Delta t}\right) d\tau \\= & {} C_{i,\sigma }^{\alpha ,n}\bigg ( \frac{W_{i+\sigma }^{\alpha ,n} -W_{i}^{\alpha ,n}}{\Delta x}\bigg ) \end{aligned}$$

where we used (3.7) and (3.9) in the last line. Using (3.8), we thus get

$$\begin{aligned} W_{i}^{\alpha ,n+1}\ge & {} \bigg (1-C_{i,\sigma }^{\alpha ,n} \frac{\Delta t}{\Delta x}\bigg ) W_{i}^{\alpha ,n} +C_{i,\sigma }^{\alpha ,n}\frac{\Delta t}{\Delta x}W_{i+\sigma }^{\alpha ,n}\\\ge & {} m^{n}. \end{aligned}$$

Case 2:$i=0$ We recall that in this case, we have $U_0^{\beta ,n}:=U_0^{n}$ and $W_0^{\beta ,n}:=W_0^n=\frac{U_0^{n+1}-U_0^n}{\Delta t}$ for any $\beta =1,\dots ,N.$ We compute in this case:

$$\begin{aligned} \frac{W_0^{n+1}-W_0^{n}}{\Delta t}= & {} \frac{1}{\Delta t} \left( -F(\{p_{0,+}^{\alpha ,n+1}\}_{\alpha }) +F(\{p_{0,+}^{\alpha ,n}\}_{\alpha })\right) \\= & {} \frac{1}{\Delta t}\int _0^1\sum _{\beta =1}^N p_\beta \frac{\partial F}{\partial p_{\beta }}\left( \{p_{0,+}^{\alpha ,n+1} +\tau p_\alpha \}_{\alpha }\right) d\tau \\&\quad \text {with} \,\,\, p =(\{p_{0,+}^{\alpha ,n}-p_{0,+}^{\alpha ,n+1}\}_{\alpha })\\= & {} -\int _0^1\sum _{\beta =1}^N\frac{\partial F}{\partial p_{\beta }} \left( \{p_{0,+}^{\alpha ,n+1}+\tau p_\alpha \}_{\alpha }\right) d\tau \bigg (\frac{W_1^{\beta ,n}-W_0^n}{\Delta x}\bigg )\\= & {} \sum _{\beta =1}^N C_{0,+}^{\beta ,n} \bigg (\frac{W_1^{\beta ,n}-W_0^n}{\Delta x}\bigg ). \end{aligned}$$

Using (3.8), we argue like in Case 1 and get

$$\begin{aligned} W_0^{n+1}\ge m^n. \end{aligned}$$

Step 2:$(M^n)_n$is non-increasing We want to show that $W_i^{\alpha ,n+1}\le M^n$ for $i\ge 0$ and $\alpha =1,\dots ,N.$ We argue as in Step 1 by distinguishing two cases.

Case 1:$i\ge 1$ We simply choose $\sigma =\sigma (i,\alpha ,n)$ (see (3.10)) and argue as in Step 1.

Case 2:$i=0$ Using (3.6), we can argue exactly as in Step 1. The proof is now complete. $\square$

3.2 Gradient estimates

The second result needed in the proof of Theorem 3.1 is the following one. It asserts that if the discrete time derivative is controlled from below, then a discrete gradient estimate holds true.

Proposition 3.3

(Discrete gradient estimate) Let $n\ge 0$ be fixed, consider that $(U_i^{\alpha ,n})_{\alpha ,i}$ is given and compute $(U_i^{\alpha ,n+1})_{\alpha ,i}$ using the scheme (1.16)–(1.17). If there exists a constant $K\in \mathbb {R}$ such that for any $i\ge 0$ and $\alpha =1,\dots , N,$

$$\begin{aligned} K\le W_i^{\alpha ,n}:=\frac{U_i^{\alpha ,n+1}-U_i^{\alpha ,n}}{\Delta t} \end{aligned}$$

then

$$\begin{aligned} \left\{ \begin{array}{rcll} \pi _\alpha ^- (-K) \le &{} p_{i,+}^{\alpha ,n} &{} \le \pi _\alpha ^+ (-K), &{} \alpha =1,\dots ,N, \quad i\ge 1, \\ \underline{\rho }_{\alpha }(-K) \le &{} p_{0,+}^{\alpha ,n} &{}\le (H_{\alpha }^{+})^{-1}(-K), &{} \alpha =1,\dots ,N \end{array}\right. \end{aligned}$$

where $p_{i,+}^{\alpha ,n}$ is defined in (1.17) and $\pi _\alpha ^{\pm }$ and $\underline{p}$ are the “generalized” inverse functions of $H_\alpha$ and F, respectively.

Proof

Let $n\ge 0$ be fixed and consider $(U_i^{\alpha ,n})_{\alpha ,i}$ with $\Delta x,\Delta t>0$ given. We compute $(U_i^{\alpha ,n+1})_{\alpha ,i}$ using the scheme (1.16). Let us consider any $i\ge 0$ and $\alpha =1,\dots ,N.$

If $i \ge 1$, the result follows from

$$\begin{aligned} K\le W_i^{\alpha ,n}=-\max _{\sigma = +,-} H_{\alpha }^{\sigma }(p_{i,-\sigma }^{\alpha ,n}). \end{aligned}$$

If $i=0$, the results follows from

$$\begin{aligned} K\le W_0^n=-F\bigg (\{p_{0,+}^{\alpha ,n}\}_\alpha \bigg ). \end{aligned}$$

This achieves the proof of Proposition 3.3$\square$

3.3 Proof of gradient estimates

Proof of Theorem 3.1

The idea of the proof is to introduce new Hamiltonians $\tilde{H_{\alpha }}$ and a new junction function $\tilde{F}$ for which it is easier to derive gradient estimates but whose corresponding numerical scheme in fact coincide with the original one.

Step 1: Modification of the Hamiltonians and the junction function Let the new Hamiltonians $\tilde{H_{\alpha }}$ for all $\alpha =1,\dots ,N$ be defined as

$$\begin{aligned} \tilde{H}_{\alpha }(p)={\left\{ \begin{array}{ll} H_{\alpha }(\underline{p}_{\alpha })+H'_{\alpha } (\underline{p}_{\alpha })(p-\underline{p}_{\alpha }) &{} \text { if } p\le \underline{p}_{\alpha }\\ H_{\alpha }(p) &{} \text { if } p\in [\underline{p}_{\alpha }\overline{p}_\alpha ]\\ H_{\alpha }(\overline{p}_{\alpha })+H'_{\alpha } (\overline{p}_{\alpha })(p-\overline{p}_\alpha ) &{} \text { if } p\ge \overline{p}_\alpha \end{array}\right. } \end{aligned}$$

(3.11)

where $\underline{p}_{\alpha }$ and $\overline{p}_\alpha$ are defined in (3.4) respectively. These new Hamiltonians are now globally Lipschitz continuous: their derivatives are bounded. More precisely, the $\tilde{H}_{\alpha }$ satisfy (1.4) and

$$\begin{aligned} \tilde{H}_\alpha \equiv H_\alpha \text { in } [\underline{p}_\alpha ,\overline{p}_\alpha ] \end{aligned}$$

and

$$\begin{aligned} \forall p \in \mathbb {R}, \quad |\tilde{H}_{\alpha }'(p)| \le \sup _{\begin{array}{c} p_{\alpha }\in [\underline{p}_{\alpha }, \overline{p}_\alpha ] \end{array}} |H_{\alpha }'(p_{\alpha })|. \end{aligned}$$

(3.12)

Let the new $\tilde{F}$ satisfy (1.8), be such that

$$\begin{aligned} \tilde{F} \equiv F \text { in } Q_0 :=\prod _{\alpha =1}^{N}[\underline{p}_{\alpha }^0,\overline{p}_\alpha ] \end{aligned}$$

and (see “Appendix A.2”)

$$\begin{aligned} \forall \mathbf {p} \in \mathbb {R}^N, \quad (-\nabla \cdot \tilde{F}) (\mathbf {p}) \le \sup _{Q_0} (-\nabla \cdot F). \end{aligned}$$

(3.13)

In the remaining of the proof, when notation contains a tilde, it is associated with the new Hamiltonians $\tilde{H}_\alpha$ and the new non-linearity $\tilde{F}$. We then consider the new numerical scheme

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\tilde{U}^{\alpha ,n+1}_i-\tilde{U}^{\alpha ,n}_i}{\Delta t} +\max \{\tilde{H}_{\alpha }^{+}(\tilde{p}_{i,-}^{\alpha ,n}), \tilde{H}_{\alpha }^{-}(\tilde{p}_{i,+}^{\alpha ,n})\}=0, &{}\quad i\ge 1, &{} \alpha =1,\dots ,N \\ \tilde{U}_0^{\beta ,n}:=U_0^n, &{}\quad i=0, &{} \beta =1,\dots ,N \\ \frac{\tilde{U}_0^{n+1}-\tilde{U}_0^{n}}{\Delta t}+\tilde{F} (\tilde{p}_{0,+}^{1,n},\tilde{p}_{0,+}^{2,n},\dots , \tilde{p}_{0,+}^{N,n})=0 &{} &{} \end{array}\right. \end{aligned}$$

with the same initial condition, namely,

$$\begin{aligned} \tilde{U}_i^{\alpha ,0}=u_0^{\alpha }(i\Delta x), \quad i\ge 0, \quad \alpha =1,\dots ,N. \end{aligned}$$

In view of (3.12) and (3.13), the CFL condition (1.20) gives that for any $i\ge 0$, $n\ge 0$, and $\alpha =1,\dots ,N$

$$\begin{aligned} \tilde{D}_{i,+}^{\alpha ,n}\le \sup \left\{ \sup _{\underline{p}_{\alpha }\le p\le \overline{p}_\alpha }{|H_{\alpha }'(p)|}; \sup _{ \tilde{I}^{\alpha ,n}_{0,+}} (-\nabla \cdot F) \right\} \le \frac{\Delta x}{\Delta t} \end{aligned}$$

(3.14)

where $\tilde{D}_{i,+}^{\alpha ,n}$ is given by (3.5) after replacing $H_\alpha$ and F with $\tilde{H}_\alpha$ and $\tilde{F}$.

Step 2: First gradient bounds Let $n\ge 0$ be fixed. If $\tilde{m}^n$ and $\tilde{M}^n$ are finite, we have

$$\begin{aligned} \tilde{m}^n\le \tilde{W}_i^{\alpha ,n}\qquad \text {for}\quad \text {any} \quad i\ge 0, \quad \alpha =1,\dots ,N . \end{aligned}$$

Proposition 3.3 implies that

$$\begin{aligned} \left\{ \begin{array}{rcll} \tilde{\pi }_\alpha ^- (-\tilde{m}^n) \le &{} \tilde{p}_{i,+}^{\alpha ,n} &{}\quad \le \tilde{\pi }_\alpha ^+ (-\tilde{m}^n), &{}\quad i\ge 1,\quad \alpha =1,\dots ,N, \\ \tilde{\underline{\rho }}_\alpha (-\tilde{m}^n) \le &{} \tilde{p}_{0,+}^{\alpha ,n} &{} \le \tilde{\pi }_\alpha ^+ (-\tilde{m}^n), &{}\quad i\ge 0,\quad \alpha =1,\dots ,N. \end{array}\right. \end{aligned}$$

In particular, we get that

$$\begin{aligned} |\tilde{p}_{i,+}^{\alpha ,n}|\le C^n \quad \text { for } \quad i\ge 0,\quad \alpha =1,\dots ,N \end{aligned}$$

with

$$\begin{aligned} C^n=\max _{\alpha } \left( \max \left( |\tilde{\pi }_\alpha ^- (-\tilde{m}^n)|,| \tilde{\pi }_\alpha ^+ (-\tilde{m}^n)|, |\tilde{\underline{\rho }}_\alpha (-\tilde{m}^n)| \right) \right) . \end{aligned}$$

In view of (3.14), Proposition 3.2 implies that

$$\begin{aligned} \tilde{m}^n\le \tilde{m}^{n+1}\le \tilde{M}^{n+1} \le \tilde{M}^{n}\,\quad \text {for} \quad \text {any}\ \ n\ge 0. \end{aligned}$$

(3.15)

In particular, $\tilde{m}^{n+1}$ is also finite. Since $\tilde{m}^0=m^0$ and $\tilde{M}^0 {=M^0}$ are finite, we conclude that $\tilde{m}^n$ and $\tilde{M}^n$ are finite for all $n \ge 0$ and for all $n \ge 0$,

$$\begin{aligned} m^0 \le \tilde{m}^n \le \tilde{M}^n \le M^0. \end{aligned}$$

(3.16)

Step 3: Time derivative and gradient estimates. Now we can repeat the same reasoning but applying Proposition 3.3 with $K=m^0$ and get

$$\begin{aligned} \left\{ \begin{array}{rcll} \underline{p}_{\alpha } \le &{} \tilde{p}_{i,+}^{\alpha ,n} &{} \le \overline{p}_\alpha , &{} i\ge 1,\quad \alpha =1,\dots ,N, \\ \underline{p}_{\alpha }^0 \le &{} \tilde{p}_{0,+}^{\alpha ,n} &{} \le \overline{p}_\alpha , &{} i\ge 0,\quad \alpha =1,\dots ,N. \end{array}\right. \end{aligned}$$

(3.17)

This implies that $\tilde{U}_i^{\alpha ,n} = U_i^{\alpha ,n}$ for all $i \ge 0$, $n \ge 0$, $\alpha = 1,\dots , N$. In view of (3.15), (3.16) and (3.17), the proof is now complete. $\square$

4 Convergence for general junction conditions

This section is devoted to the convergence of the scheme defined by (1.16)–(1.17).

4.1 Monotonicity of the scheme

In order to prove the convergence of the numerical solution as the mesh size tends to zero, we need first to prove a monotonicity result. It is common to write the scheme defined by (1.16)–(1.17) under the compact form

$$\begin{aligned} u^h (t+\Delta t,x) = S^h [u^h(t)](x) \end{aligned}$$

where the operator $S^h$ is defined on the set of functions defined in $J^h$. The scheme is monotone if

$$\begin{aligned} u \le v \quad \Rightarrow \quad S^h [u] \le S^h [v]. \end{aligned}$$

In our cases, if $t = n \Delta t$ and $x = i\Delta x \in J^{\alpha }$ and $U(t,x) = U^{\alpha ,n}_i$ for $x \in J^{\alpha }$, then $S^h[U]$ is defined as follows,

$$\begin{aligned} {\left\{ \begin{array}{ll} U_i^{\alpha ,n+1}=S_{\alpha }[U_{i-1}^{\alpha ,n}, U_i^{\alpha ,n},U_{i+1}^{\alpha ,n}]\quad \text { for } i\ge 1, \,\alpha =1,\dots ,N, \\ U_0^{n+1}=S_{0}[U_0^{n},(U_1^{\beta ,n})_{\beta =1,\dots ,N}] \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{array}{lll} S_{\alpha }[U_{i-1}^{\alpha ,n},U_i^{\alpha ,n},U_{i+1}^{\alpha ,n}] :=U_i^{\alpha ,n}-\Delta t \max \left\{ H_{\alpha }^{+} \left( \frac{U_i^{\alpha ,n}-U_{i-1}^{\alpha ,n}}{\Delta x}\right) , H_{\alpha }^{-}\left( \frac{U_{i+1}^{\alpha ,n}-U_{i}^{\alpha ,n}}{\Delta x}\right) \right\} , \\ S_{0}[U_0^{n},(U_1^{\beta ,n})_{\beta =1,\dots ,N}] :=U_0^{n}-\Delta t F(p_{0,+}^{1,n},\dots ,p_{0,+}^{N,n}) \end{array}\right. \end{aligned}$$

(4.1)

Checking the monotonicity of the scheme reduces to checking that $S_{\alpha }$ and $S_0$ are non-decreasing in all their variables.

Lemma 4.1

(Monotonicity of the numerical scheme) Let $(U^n):=(U_i^{\alpha ,n})_{\alpha ,i}$ the numerical solution of (1.16)–(1.18). Under the CFL condition (1.19) the scheme is monotone.

Proof

We distinguish two cases.

Case 1$i\ge 1$. It is straightforward to check that, for any $\alpha =1,\dots ,N,$ the function $S_{\alpha }$ is non-decreasing with respect to $U^{\alpha ,n}_{i-1}$ and $U_{i+1}^{\alpha ,n}$. Moreover,

$$\begin{aligned} \frac{\partial S_{\alpha }}{\partial U_i^{\alpha ,n}} =\left\{ \begin{array}{l} 1-\frac{\Delta t}{\Delta x}(H_{\alpha }^{+})'(p_{i,-}^{\alpha ,n}) \quad \text { if } \quad \max \{H_{\alpha }^{+}(p_{i,-}^{\alpha ,n}), H_{\alpha }^{-}(p_{i,+}^{\alpha ,n})\}=H_{\alpha }^{+}(p_{i,-}^{\alpha ,n})\\ 1+\frac{\Delta t}{\Delta x}(H_{\alpha }^{-})'(p_{i,+}^{\alpha ,n}) \quad \text { if } \quad \max \{H_{\alpha }^{+}(p_{i,-}^{\alpha ,n}), H_{\alpha }^{-}(p_{i,+}^{\alpha ,n})\}=H_{\alpha }^{-}(p_{i,+}^{\alpha ,n}) \end{array}\right. \end{aligned}$$

which is non-negative if the CFL condition (1.19) is satisfied.

Case 2$i=0$. Similarly it is straightforward to check that $S_0$ is non-decreasing with respect to $U_1^{\beta ,n}$ for $\beta =1,\dots ,N$. Moreover,

$$\begin{aligned} \frac{\partial S_0}{\partial U_0^n}=1+\frac{\Delta t}{\Delta x} \sum _{\beta =1}^{N} \frac{\partial F}{\partial p_{\beta }} \{ (p_{0,+}^{\alpha ,n})_{\alpha =1}^{N}\} \end{aligned}$$

which is non-negative due to the CFL condition. The proof is now complete. $\square$

A direct consequence of the previous lemma is the following elementary but useful discrete comparison principle.

Lemma 4.2

(Discrete Comparison Principle) Let $(U^n):=(U_i^{\alpha ,n})_{\alpha ,i}$ and $(V^n):=(V_i^{\alpha ,n})_{\alpha ,i}$ be such that

$$\begin{aligned} \forall n \ge 1, \quad U^{n+1} \le S^h [U^n] \quad \text { and } \quad V^{n+1} \ge S^h [V^n]. \end{aligned}$$

If the CFL condition (1.19) is satisfied and if $U^0 \le V^0$, then $U^n\le V^n$ for all $n \in \mathbb {N}$.

Remark 4

The discrete function $(U^n)$ (resp. $(V^n)$) can be seen as a sub-scheme (resp. super-scheme).

We finally recall how to derive discrete viscosity inequalities for monotone schemes.

Lemma 4.3

(Discrete viscosity inequalities) Let $u^h$ be a solution of (1.16)–(1.18) with $F=F_{A}$ defined in (1.5). Then $u^h$ is a discrete sub-solution (resp. super-solution) in the following sense. If $u^h-\varphi$ has a global maximum (resp. global minimum) on $\mathcal {G}_h$ defined in (1.15) at $(\overline{t}+\Delta t,\overline{x})$, then

$$\begin{aligned} \delta _t\varphi (\overline{t},\overline{x}) +\mathcal {H}(\overline{x},D_{+}\varphi (\overline{t}, \overline{x}),D_{-}\varphi (\overline{t},\overline{x}))\le 0. \quad (\text {resp. } \ge 0) \end{aligned}$$

where

$$\begin{aligned} \mathcal {H}(x,p_+,p_-)={\left\{ \begin{array}{ll} \max \{H_{\alpha }^{+}(p_-),H_{\alpha }^{-}(p_+)\} &{} \text { if }\; \overline{x}\ne 0\\ \max \{A,\max _\alpha H_{\alpha }^{-}(p^+_\alpha )\} &{} \text { if }\; \overline{x}=0 \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} D_{+}\varphi (\overline{t},\overline{x})= & {} {\left\{ \begin{array}{ll} \frac{1}{\Delta x}\{\varphi (\overline{t},\overline{x}+\Delta x) -\varphi (\overline{t},\overline{x})\} &{} \text { if }\; \overline{x} \ne 0 \\ \left( \frac{1}{\Delta x}\{\varphi ^{\alpha }(\overline{t},\Delta x) -\varphi ^{\alpha }(\overline{t},0)\} \right) _\alpha &{} \text { if }\; \overline{x} = 0 \end{array}\right. }\\ D_{-}\varphi (\overline{t},\overline{x})= & {} \frac{1}{\Delta x}\{\varphi (\overline{t},\overline{x}) -\varphi (\overline{t},\overline{x}-\Delta x)\}\\ \delta _t\varphi (\overline{t},\overline{x})= & {} \frac{1}{\Delta t}\{\varphi (\overline{t}+\Delta t,\overline{x}) -\varphi (\overline{t},\overline{x})\}. \end{aligned}$$

We say that $u^h$ is a discrete subsolution (resp. supersolution).

4.2 Stability and consistency of the scheme

We first derive a local $L^{\infty }$ bound for the solution of the scheme.

Lemma 4.4

(Stability of the numerical scheme) Assume that the CFL condition (1.20) is satisfied and let $u^h$ be the solution of the numerical scheme (1.16)–(1.18). There exists a constant $C_0>0$, such that for all $(t,x) \in \mathcal {G}_h$,

$$\begin{aligned} |u^h (t,x) -u_0 (x)|\le C_0 t. \end{aligned}$$

(4.2)

In particular, the scheme is (locally) stable.

Proof

If $C_0$ large enough so that

$$\begin{aligned} \left\{ \begin{array}{lll} C_0 +\max \{H_{\alpha }^{+}(p_{i,-}^{\alpha ,0}),H_{\alpha }^{-} (p_{i,+}^{\alpha ,0})\} \ge 0, &{}\quad i\ge 1, &{} \alpha =1,\dots ,N\\ C_0 +F(p_{0,+}^{1,0},p_{0,+}^{2,0},\dots ,p_{0,+}^{N,0}) \ge 0, &{} &{} \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{lll} -C_0 +\max \{H_{\alpha }^{+}(p_{i,-}^{\alpha ,0}),H_{\alpha }^{-} (p_{i,+}^{\alpha ,0})\} \le 0, &{}\quad i\ge 1, &{} \alpha =1,\dots ,N\\ - C_0 +F(p_{0,+}^{1,0},p_{0,+}^{2,0},\dots ,p_{0,+}^{N,0}) \le 0, &{} &{} \end{array}\right. \end{aligned}$$

then $\bar{U}^{\alpha ,n}_i = U^{\alpha ,0}_i + C_0 n \Delta t$ is a super-scheme and $\bar{U}^{\alpha ,n}_i = U^{\alpha ,0}_i - C_0 n \Delta t$ is a sub-scheme (see Remark 4). The discrete comparison principle, Lemma 4.2, then implies

$$\begin{aligned} |U^{\alpha ,n}_i -U^{\alpha ,0}_i | \le C_0 n \Delta t \end{aligned}$$

which is the desired inequality. This achieves the proof. $\square$

Another condition to satisfy convergence of the numerical scheme (1.16) towards the continuous solution of (1.6) is the consistency of the scheme (which is obvious in our case).

Lemma 4.5

(Consistency of the numerical scheme) Under the assumptions on the Hamiltonians (1.4), the finite difference scheme is consistent with the continuous problem (1.6), that is to say for any smooth function $\varphi (t,x),$ we have locally uniformly

$$\begin{aligned} \frac{S^h[\varphi ](s,y) -\varphi (s,y)}{\Delta t} \rightarrow H_\alpha (\varphi _x(t,x)) \quad \text {as}\quad \mathcal {G}_h \ni (s,y) \rightarrow (t,x) \end{aligned}$$

if $x \in J_\alpha ^{\star }$, and

$$\begin{aligned} \frac{S^h[\varphi ](s,y) -\varphi (s,y)}{\Delta t} \rightarrow F \left( \frac{\partial \varphi }{\partial x_{1}},\dots ,\frac{\partial \varphi }{\partial x_{N}}(t,0)\right) \quad \text {as}\quad \mathcal {G}_h \ni (s,y) \rightarrow (t,0). \end{aligned}$$

4.3 Convergence of the numerical scheme

In this subsection, we present a sketch of the proof of Theorem 1.1.

Sketch of the proof of Theorem 1.1 Let $T > 0$ and $h := (\Delta t, \Delta x)$ satisfying the CFL condition (1.20). We recall that

$$\begin{aligned} u^h (0,x) = u(0,x) \quad \text { for } \quad x \in \mathcal {G}_h. \end{aligned}$$

We consider $\overline{u}$ and $\underline{u}$ respectively defined as

$$\begin{aligned} \overline{u}(t,y)= \limsup _{\begin{array}{c} h\rightarrow 0\\ \mathcal {G}_{h} \ni (t',y')\rightarrow (t,y) \end{array}}u^{h}(t',y'), \qquad \underline{u}(t,y) = \liminf _{\begin{array}{c} h\rightarrow 0\\ \mathcal {G}_{h}\ni (t',y')\rightarrow (t,y) \end{array}} u^{h}(t',y'). \end{aligned}$$

By construction, we have $\underline{u} \le \overline{u}$. Since the scheme is monotone (Lemma 4.1), stable (Lemma 4.4) and consistent (Lemma 4.5), we can follow [6, 16] we can show that $\underline{u}$ (resp. $\overline{u}$) is a relaxed viscosity super-solution (resp. viscosity sub-solution) of equation (1.1)–(1.2), see for example the proof of [16, Theorem 1.8]. Using Theorem 2.2, we know that $\underline{u}$ (resp. $\overline{u}$) is a viscosity super-solution (resp. sub-solution) of (1.6)–(1.2). Moreover, (4.2) implies that

$$\begin{aligned} \overline{u} (0,x) \le u_0 (x) \le \underline{u} (0,x). \end{aligned}$$

The comparison principle (see Theorem 2.1) then implies that

$$\begin{aligned} \overline{u} \le u \le \underline{u} \end{aligned}$$

which achieves the proof. $\square$

5 Study of the reduced minimal action

In this section, we consider that the Hamiltonians $H_{\alpha }$ satisfy (1.10). We study the reduced minimal action $\mathcal {D}_{0}$ which replaces the classical term $\frac{(x-y)^{2}}{2\epsilon }$ in the doubling variable method. This function allows us to prove that the error estimate is of order $(\Delta x)^{\frac{1}{2}}$.

5.1 Reduction of the study

We start this section by the following remark, the analysis can be reduced to the case $(s,t)=(0,1).$ Precisely, using the fact that the Hamiltonian does not depend on time and is homogeneous with respect to the state, the reader can check that a change of variables in time yields the following Lemma.

Lemma 5.1

For all $y,x \in J$ and $s<t,$ we have

$$\begin{aligned} \mathcal {D}(s,y;t,x)=(t-s)\mathcal {D}\bigg (0,\frac{y}{t-s};1, \frac{x}{t-s}\bigg ). \end{aligned}$$

where

$$\begin{aligned} \mathcal {D}(s,y;t,x)=\inf _{\begin{array}{c} {X\in \mathcal {A}(s,y;t,x)} \end{array}}\bigg \{\int _s^t L(X(\tau ),\dot{X}(\tau ))d\tau \bigg \}. \end{aligned}$$

This is the reason why we consider the reduced minimal action $\mathcal {D}_0: J^2\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \mathcal {D}_0(y,x)=\mathcal {D}(0,y;1,x). \end{aligned}$$

(5.1)

We also need the following lower bound on $\mathcal {D}.$

Lemma 5.2

Assume (B0). Then

$$\begin{aligned} \mathcal {D}(s,y;t,x)\ge \frac{\gamma }{2(t-s)}d^2(x,y)-A(t-s) \end{aligned}$$

where $\gamma$ is defined in (B0).

Moreover,

$$\begin{aligned} \mathcal {D}(s,x;t,x)\le \tilde{L}_{A}(p)(t-s). \end{aligned}$$

Proof

We only prove the first inequality since the other inequality is elementary. As $L'_{\alpha }(0)=0$, and $L_{\alpha }(0)\ge \tilde{L}_{A}(p)=-A$, we have

$$\begin{aligned} L_{\alpha }(p)\ge \frac{\gamma }{2}p^2+L_{\alpha }^{\prime }(0)p+L_{\alpha }(0)\ge \frac{\gamma }{2}p^2-A. \end{aligned}$$

Thus, we can write for $X(.)\in \mathcal {A}(s,y;t,x),$

$$\begin{aligned} \int _s^tL(X(\tau ),\dot{X}(\tau ))d\tau \ge -A(t-s)+\frac{\gamma }{2}\int _s^t(\dot{X}(\tau ))^{2}d\tau . \end{aligned}$$

Then Jensen’s inequality allows us to conclude. $\square$

5.2 Piecewise linear trajectories

We are going to see that the infimum defining the minimal action can be computed among piecewise linear trajectories. In order to provide a precise statement, we first observe that optimal curves in (1.14) are of two types depending on the position of y and x on the same branch or not: if they are, then the trajectories are of two types: either they reach the junction point, or they stay in a branch and are straight lines. For $y\in J_{\beta },$$x\in J_{\alpha }$ with $\beta \ne \alpha ,$ the trajectories can spend some time at the junction point.

Lemma 5.3

The infimum defining the reduced minimal action $\mathcal {D}_0$ can be computed among piecewise linear trajectories; more precisely for all $y,x\in J,$

$$\begin{aligned} \mathcal {D}_0(y,x)=\left\{ \begin{array}{ll} \mathcal {D}_{{ junction}}(y,x) &{}\quad \text { if }\; \alpha \ne \beta ,\\ \min (L_{\alpha }(x-y),\mathcal {D}_{{ junction}}(y,x)) &{}\quad \text { if }\; \alpha =\beta , \end{array}\right. \end{aligned}$$

(5.2)

where for $x\in J_{\alpha }, y\in J_{\beta }$

$$\begin{aligned} \mathcal {D}_{{ junction}}(y,x)=\inf _{\begin{array}{c} {0\le t_1\le t_2 \le 1} \end{array}} \bigg \{t_{1}L_{\beta }\bigg (\frac{-y}{t_1}\bigg )+(t_2-t_1) \tilde{L}_{A}(p)+(1-t_2)L_{\alpha }\bigg (\frac{x}{1-t_2}\bigg )\bigg \}. \end{aligned}$$

(5.3)

Proof

We write $\mathcal {D}_0=\inf _{\begin{array}{c} {X\in \mathcal {A}_0(y,x)} \end{array}}\Lambda (X),$ where $\Lambda (X)=\int _{0}^{1}L(X(\tau ), \dot{X}(\tau ))d\tau .$ In order to prove the lemma, it is enough to consider a curve $X\in \mathcal {A}(0,y;1,x)$ and prove that

$$\begin{aligned} \Lambda (X)\ge \min (L_{\alpha }(x-y), D_{{ junction}}(y,x)). \end{aligned}$$

For $\alpha \ne \beta ,$ the trajectories can spend some time at the junction point, hence we can write

$$\begin{aligned} \mathcal {D}_0(y,x)= & {} \inf _{\begin{array}{c} {X(0)=y}\\ {X(1)=x} \end{array}}\bigg \{\int _0^{t_1}L_{\beta } (\dot{X}(\tau ))d\tau +\int _{t_1}^{t_2}L(X(\tau ), \dot{X}(\tau ))d\tau +\int _{t_2}^{1}L_{\alpha }(\dot{X}(\tau ))d\tau \bigg \} \\\ge & {} \inf _{\begin{array}{c} 0\le t_1\le t_2\le 1 \end{array}} \bigg \{\inf _{\begin{array}{c} {X(0)=y}\\ {X(t_1)=0} \end{array}} \int _0^{t_1}L_{\beta }(\dot{X}(\tau ))d\tau +\inf _{\begin{array}{c} {X(t_1)=0}\\ {X(t_2)=0} \end{array}} \int _{t_1}^{t_2}L(X(\tau ), \dot{X}(\tau ))d\tau \\&+\inf _{\begin{array}{c} {X(t_2)=0}\\ {X(1)=x} \end{array}}\int _{t_2}^{1} L_{\alpha }(\dot{X}(\tau ))d\tau \bigg \} \end{aligned}$$

then using that $L\ge \tilde{L}_{A}$ for the second term and Jensen’s inequality for all terms, we conclude that

$$\begin{aligned} \mathcal {D}_0(y,x)\ge \mathcal {D}_{{ junction}}(y,x). \end{aligned}$$

Now for $\alpha =\beta ,$ we can deduce from the preceding that

$$\begin{aligned} \mathcal {D}_0(y,x)\ge \min \left( \mathcal {D}_{{ junction}}(y,x), \inf _{\begin{array}{c} {X(0)=y}\\ {X(1)=x} \end{array}}\int _{0}^{1}L_{\alpha } (\dot{X}(\tau ))d\tau \right) . \end{aligned}$$

Then, by Jensen’s inequality once again, we can deduce (5.2). This ends the proof. $\square$

In view of (5.2), we see that the study of $\mathcal {D}_0$ can now be reduced to the study of $\mathcal {D}_{{ junction}}.$

5.3 Study of $\mathcal {D}_{{ junction}}$

We introduce a simpler notation of $\mathcal {D}_{{ junction}}$ defined in (5.3),

$$\begin{aligned} \mathcal {D}_{{ junction}}(y,x)=\inf _{\begin{array}{c} 0\le t_1\le t_2\le 1 \end{array}} G(t_1,t_2,y,x), \end{aligned}$$

(5.4)

where

$$\begin{aligned} G(t_{1},t_{2},y,x)= t_{1}L_{\beta }\bigg (\frac{-y}{t_1}\bigg ) +(t_2-t_1)\tilde{L}_{A}(p)+(1-t_2)L_{\alpha }\bigg (\frac{x}{1-t_2}\bigg ). \end{aligned}$$

As in [26], for $(y,x)\in J_{\beta }^{\star }\times J_{\alpha }^{\star }$ the function $(t_{1},t_{2})\rightarrow G(t_{1},t_{2},y,x)$ is stricly convex on $(0,1)\times (0,1)$. Indeed, for $t_{1},t_{2}\in (0,1)$, we compute

$$\begin{aligned} D^{2}G(t_{1},t_{2},y,x)=\frac{L''_{\beta }\left( \frac{-y}{t_{1}}\right) }{t_{1}}V_{y}^{T}V_{y}+\frac{L''_{\alpha } \left( \frac{x}{1-t_{1}}\right) }{1-t_{2}}V_{x}^{T}V_{x}\ge 0, \end{aligned}$$

where $V_{y}=(\frac{-y}{t_{1}},0,1,0)$ and $V_{x}=(0,\frac{x}{1-t_{1}},0,1)$ and in particular, we have

$$\begin{aligned} \frac{\partial ^2}{\partial t_1^2}G(t_{1},t_{2},y,x) =\frac{y^{2}}{t_{1}^{3}}L''_{\beta }\left( \frac{-y}{t_{1}}\right) > 0, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2}{\partial t_2^2}G(t_{1},t_{2},y,x) =\frac{x^{2}}{(1-t_{2})^{3}}L''_{\alpha } \left( \frac{x}{1-t_{1}}\right) > 0. \end{aligned}$$

So we deduce that for $(y,x)\in J_{\beta }^{\star }\times J_{\alpha }^{\star }$, if the function $(t_{1},t_{2})\rightarrow G(t_{1},t_{2},y,x)$ admits a critical point, then it reaches its infimum at this point, else it reaches its infimum at the boundary.

Lemma 5.4

Let $(y,x)\in J,$ and $D_{{ junction}}(y,x)$ as in (5.3). We have the following equivalences for the infimum,

$$\begin{aligned} \left\{ \begin{array}{ll} x=0 \Leftrightarrow t_2=1,\\ y=0 \Leftrightarrow t_1=0. \end{array}\right. \end{aligned}$$

Proof

It is a direct consequence of the expression (5.3). $\square$

Definition 3

(Numbers$\xi _{\alpha }^{+}, \xi _{\alpha }^{-}$) We define $\xi _{\alpha }^{-},$$\xi _{\alpha }^{+}$ thanks to the following function (for $l\in \{1,\ldots N\}$)

$$\begin{aligned} K_{\alpha }(x)=L_{\alpha }(x) -xL_{\alpha }^{\prime }(x)-\tilde{L}_{A}(p). \end{aligned}$$

(5.5)

We define $(K_{\alpha }^{-})^{-1}$ (resp. $(K_{\alpha }^{+})^{-1}$) as the inverse of the function $K_{\alpha }$ restricted to $(-\infty ,0]$ (resp. $[0, +\,\infty )$), in fact one can write

$$\begin{aligned} K_{\alpha }^{\prime }(x)=-xL_{\alpha }^{\prime \prime }(x)<0 \text { on } (0,+\,\infty )\quad (\text { resp. }>0 \text { on } (-\infty ,0)). \end{aligned}$$

More precisely, we define $\xi _{\alpha }^{\pm }=(K_{\alpha }^{\pm })^{-1}(0).$

Lemma 5.5

(Explicit expression of $\mathcal {D}_{{ junction}}(y,x)$) It exists a unique function $\tau :J\times J \rightarrow (0,1)$ of class $\mathcal {C}^{1}$ such that for $(y,x)\in J_{\beta }\times J_{\alpha },$ we have

$$\begin{aligned}&\mathcal {D}_{{ junction}}(y,x)\nonumber \\&\quad = \left\{ \begin{array}{ll} \tau (y,x) L_{\beta }\left( \frac{-y}{\tau (y,x)}\right) +(1-\tau (y,x))L_{\alpha }\left( \frac{x}{1-\tau (y,x)}\right) &{} \text { if } (y,x)\in (J_{\beta }^{\star }\times J_{\alpha }^{\star }){\setminus } \Delta _{\beta \alpha },\\ -yL_{\beta }^{\prime }(\xi _{\beta }^{-})+xL_{\alpha }^{\prime } (\xi _{\alpha }^{+})+\tilde{L}_{A}(p) &{} \text { if } (y,x) \in \Delta _{\beta \alpha },\\ L_{\alpha }(x) &{} \text { if } y=0 \text { and } x>\xi _{\alpha }^{+},\\ L_{\beta }(-y) &{} \text { if } x=0 \text { and } y>-\xi _{\beta }^{-}, \end{array}\right. \end{aligned}$$

(5.6)

where

$$\begin{aligned} \Delta _{\beta \alpha }=\bigg \{(y,x)\in J_{\beta } \times J_{\alpha }, \quad \frac{x}{\xi _{\alpha }^{+}} -\frac{y}{\xi _{\beta }^{-}}\le 1 \bigg \}. \end{aligned}$$

Fig. 1

Subsets of $\mathcal {D}_{{ junction}}$ for $\alpha \ne \beta$

We have a different expression of $\mathcal {D}_{{ junction}}$ on each subset of the previous Lemma (see Fig. 1).

Proof

Writing the optimal conditions of G associated with the infimum in (5.4), we have

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{y}{t_1}L_{\beta }^{\prime }\left( \frac{-y}{t_1}\right) -\tilde{L}_{A}(p)+L_{\beta }\left( \frac{-y}{t_1}\right) =0,\\ \\ -\frac{x}{1-t_2}L_{\alpha }^{\prime }\left( \frac{x}{1-t_2}\right) -\tilde{L}_{A}(p)+L_{\alpha }\left( \frac{x}{1-t_2}\right) =0, \end{array}\right. \end{aligned}$$

(5.7)

where $t_1$ and $t_2$ are the quantities realizing the minimum. Hence from (5.7), we deduce

$$\begin{aligned} K_{\beta }\left( -\frac{y}{t_1}\right) =0=K_{\alpha } \left( \frac{x}{1-t_2}\right) . \end{aligned}$$

But $K_{\beta }$ is a bijection on $(-\infty ,0),$ and so is $K_{\alpha }$ on $(0,+\,\infty ).$ Therefore, setting $(K_{\beta }^{-})^{-1}(0):=\xi _{\beta }^{-},$ and $(K_{\alpha }^{+})^{-1}(0):=\xi _{\alpha }^{+},$ we deduce for $(y,x)\in \Delta _{\beta \alpha }\backslash \{xy=0\},$

$$\begin{aligned} \mathcal {D}_{{ junction}}(y,x)= & {} \frac{-y}{\xi _{\beta }^-}L_{\beta } (\xi _{\beta }^{-})+\frac{x}{\xi _{\alpha }^{+}}L_{\alpha }(\xi _{\alpha }^{+}) +\left( 1-\frac{x}{\xi _{\alpha }^+}+\frac{y}{\xi _{\beta }^{-}}\right) \tilde{L}_{A}(p)\\= & {} -yL_{\beta } ^{\prime }(\xi _{\beta } ^{-})+xL_{\alpha }^{\prime } (\xi _{\alpha }^{+})+\tilde{L}_{A}(p). \end{aligned}$$

Now, for $x=0$ and $y<-\xi _{\beta }^{-}$, using the first condition of (5.7), we deduce that

$$\begin{aligned} \mathcal {D}_{{ junction}}(y,0)=-yL_{\beta } ^{\prime } (\xi _{\beta }^{-})+\tilde{L}_{A}(p). \end{aligned}$$

For $x=0$ and $y\ge -\xi _{\beta }^{-},$ we deduce from Lemma 5.4, that $t_2=1$. Using the first optimal condition in (5.7), we have $K_{\beta }\left( \frac{-y}{t_{1}} \right) =0$ so $t_{1}=\frac{-y}{\xi _{\beta }^{-}}\ge 1$. We deduce that the optimal condition must be satisfied at the boundary of the set $\{0\le t_{1}\le 1\}$. Here using (5.3), we have $t_{1}=1$, so

$$\begin{aligned} D_{{ junction}}(y,0)=L_{\beta }(-y). \end{aligned}$$

Similarly, for $y=0$ and $x< \xi _{\alpha }^{+},$

$$\begin{aligned} \mathcal {D}_{{ junction}}(y,x) = xL_{\alpha }^{\prime } (\xi _{\alpha }^{+})+\tilde{L}_{A}(p). \end{aligned}$$

For $y=0$ and $x\ge \xi _{\alpha }^{+},$ we deduce that

$$\begin{aligned} \mathcal {D}_{{ junction}}(0,x)=L_{\alpha }(x). \end{aligned}$$

In all other cases, that is to say for $(y,x)\in (J_{\beta }^{\star }\times J_{\alpha }^{\star }){\setminus } \Delta _{\beta \alpha },$ the infimum of G is attained at the boundary of $\{0\le t_{1} \le t_{2}\le 1 \}$, here for some $t_{1}=t_{2}=\tau \in (0,1).$ Hence we have

$$\begin{aligned} \mathcal {D}_{{ junction}}(y,x)=\inf _{\begin{array}{c} 0< \tau < 1 \end{array}} \bigg \{\tau L_{\beta }\left( \frac{-y}{\tau }\right) +(1-\tau )L_{\alpha } \left( \frac{x}{1-\tau }\right) \bigg \} \end{aligned}$$

Once again, writing the optimal conditions for $G(\tau ,\tau ,y,x),$ we deduce that

$$\begin{aligned} K_{\beta }\left( \frac{-y}{\tau }\right) =K_{\alpha } \left( \frac{x}{1-\tau }.\right) . \end{aligned}$$

(5.8)

We define

$$\begin{aligned} \tilde{G}(\tau ,y,x)=K_{\beta }\left( \frac{-y}{\tau }\right) -K_{\alpha }\left( \frac{x}{1-\tau }\right) . \end{aligned}$$

Deriving

$$\begin{aligned} \frac{\partial \tilde{G}}{\partial \tau }=K_{\beta }^{\prime } \left( \frac{-y}{\tau }\right) \frac{y}{\tau ^2}-K_{\alpha }^{\prime } \left( \frac{x}{1-\tau }\right) \frac{x}{(1-\tau )^2}>0 \quad \text{ for } (y,x)\in (J_{\beta }^{\star }\times J_{\alpha }^{\star }){\setminus } \Delta _{\beta \alpha }, \end{aligned}$$

by implicit function theorem, we deduce that there exists a unique $\tilde{\tau }\in C^1(0,1)$ satisfying $\tilde{G}(\tilde{\tau }, y,x)=0.$ The proof is thus complete. $\square$

Lemma 5.6

(Continuity of $\mathcal {D}_{{ junction}}$) The function $\mathcal {D}_{{ junction}}$ is continuous in $J^2.$

Proof

From (5.6), we already know that $\mathcal {D}_{{ junction}}\in C((J_{\beta }^{\star }\times J_{\alpha }^{\star })\backslash \Delta _{\beta \alpha })\cup C(\Delta _{\beta \alpha }\cup \{ x=0\}\cup \{ y=0\}).$ Therefore in order to prove that $\mathcal {D}_{{ junction}}\in C(J_{\beta }\times J_{\alpha }),$ it is sufficient to prove that for any given sequence $(y^k,x^k)\in (J_{\beta }^{\star }\times J_{\alpha }^{\star }){\setminus } \Delta _{\beta \alpha }$ such that $(y^k,x^k)\rightarrow (y,x),$ where $(y,x)\in \bar{\Delta }:=\{\frac{x}{\xi _{\alpha }^{+}}-\frac{y}{\xi _{\beta }^{-}} = 1\}\cup \{ x\ge \xi _{\alpha }^{+}\}\cup \{ y\ge -\xi _{\beta }^{-}\},$ we have

$$\begin{aligned} \mathcal {D}_{{ junction}}(y^k,x^k)\rightarrow \mathcal {D}_{{ junction}}(y,x). \end{aligned}$$

Since the sequence $\{\tau (y^{k},x^{k})\}$ is bounded, we can deduce that there exists a sub-sequence such that $\tau (y^k,x^k)\rightarrow \tau ^0.$ We distinguish the following cases.

Case 1$\tau ^0\in (0,1)$. By continuity of $K_{\alpha },$ we have

$$\begin{aligned} K_{\alpha }\left( \frac{x}{1-\tau ^0}\right) =K_{\beta } \left( \frac{-y}{\tau ^0}\right) . \end{aligned}$$

(5.9)

If $x=0,$ we have as $K_{\alpha }(0)>0$ and $(K_{\beta }^{-})^{-1}$ is increasing

$$\begin{aligned} \frac{y}{\tau ^0}=-(K_{\beta }^{-})^{-1}(K_{\alpha })(0) < -(K_{\beta }^{-})^{-1} (0)=-\xi _{\beta }^{-}, \end{aligned}$$

hence deduce that $(y,0)\notin \bar{\Delta } ,$ so this case is not possible.

Similarly, if $y=0,$ we have

$$\begin{aligned} \frac{x}{1-\tau ^0}=(K_{\alpha }^{+})^{-1}(K_{\beta })(0) < (K_{\alpha }^{+})^{-1} (0) =\xi _{\alpha }^{+}, \end{aligned}$$

hence deduce that $(0,x)\notin \bar{\Delta } ,$ so this case is not possible.

Now if $(y,x)\in (J_{\beta }^{\star }\times J_{\alpha }^{\star })\cap \bar{\Delta },$ then $\frac{x}{\xi _{\alpha }^{+}} -\frac{y}{\xi _{\beta }^{-}} = 1$ and passing to the limit, we have (5.9). We know that $K_{\alpha }(\xi _{\alpha }^{+}) =K_{\beta }(\xi _{\beta }^{-})=0$, so if we set $\bar{\tau }=-\frac{y}{\xi _{\beta }^{-}}=1-\frac{x}{\xi _{\alpha }^{+}}$ so $1-\bar{\tau }=\frac{x}{\xi _{\alpha }^{+}}$, we have

$$\begin{aligned} K_{\beta }\left( \frac{-y}{\bar{\tau }}\right) =0=K_{\alpha } \left( \frac{x}{1-\bar{\tau }} \right) . \end{aligned}$$

(5.10)

By uniqueness of $\tau$ satisfying (5.8), we deduce that $\tau ^{0}=\bar{\tau }$. So we have

$$\begin{aligned} \mathcal {D}_{{ junction}}(y^{k},x^{k})\rightarrow -yL_{\beta }^{\prime }(\xi _{\beta }^{-})+xL_{\alpha }^{\prime } (\xi _{\alpha }^{+})+\tilde{L}_{A}(p)=\mathcal {D}_{{ junction}}(y,x). \end{aligned}$$

Case 2:$\tau ^0=0$. In this case using Lemma 5.4, $y^k\rightarrow y=0,$ so $x\ge \xi _{\alpha }^{+}$ and with (5.8) we deduce that

$$\begin{aligned} \frac{-y^k}{\tau (y^k,x^k)}=(K_{\beta }^{-})^{-1} \left( K_{\alpha }\left( \frac{x^{k}}{1-\tau (y^{k},x^{k})}\right) \right) \rightarrow (K_{\beta }^{-})^{-1}\left( K_{\alpha }\left( x\right) \right) . \end{aligned}$$

(5.11)

Therefore $\mathcal {D}_{{ junction}}(y^{k},x^{k})\rightarrow L_{\alpha }(x)=\mathcal {D}_{{ junction}}(0,x).$

Case 3$\tau ^0=1$. In this case, $x^k\rightarrow x=0.$ Arguing as in Case 2, we deduce that $y\ge \xi _{\beta }^{-}$, and

$$\begin{aligned} \frac{x^{k}}{1-\tau (y^{k},x^{k})}=(K_{\alpha }^{+})^{-1} \left( K_{\beta }\left( \frac{-y^k}{\tau (y^k,x^k)}\right) \right) \rightarrow (K_{\alpha }^{+})^{-1}\left( K_{\beta }\left( -y\right) \right) . \end{aligned}$$

(5.12)

Therefore, $\mathcal {D}_{{ junction}}(y^{k},x^{k}) \rightarrow L_{\beta }(-y)=\mathcal {D}_{{ junction}}(y,x)$.

The proof is thus complete. $\square$

Lemma 5.7

The function $\mathcal {D}_{{ junction}}$ is $C^{1}$ in $J^2$ and for $(y,x)\in J_{\beta }\times J_{\alpha },$ we have

$$\begin{aligned} \partial _{x}\mathcal {D}_{{ junction}}(y,x)= \left\{ \begin{array}{l@{\quad }l} L_{\alpha }^{\prime }(\frac{x}{1-\tau })&{} \text { if } (y,x) \in (J_{\beta }^{\star }\times J_{\alpha }^{\star }){\setminus } \Delta _{\beta \alpha },\\ L_{\alpha }^{\prime }(\xi _{\alpha }^{+})&{} \text { if } (y,x) \in \Delta _{\beta \alpha },\\ L_{\alpha }^{\prime }(x) &{} \text { if } y=0 \text { and } x>\xi _{\alpha }^{+},\\ L_{\alpha }^{\prime }\circ (K_{\alpha }^{+})^{-1} \circ K_{\beta }(-y) &{} \text { if } x=0 \text { and } y>-\xi _{\beta }^{-}, \end{array}\right. \end{aligned}$$

(5.13)

and

$$\begin{aligned} \partial _{y}\mathcal {D}_{{ junction}}(y,x)= \left\{ \begin{array}{l@{\quad }l} -L_{\beta }^{\prime }(\frac{-y}{\tau })&{} \text { if } (y,x) \in (J_{\beta }^{\star }\times J_{\alpha }^{\star }) {\setminus } \Delta _{\beta \alpha },\\ -L_{\beta }^{\prime }(\xi _{\beta }^{-}) &{} \text { if } (y,x)\in \Delta _{\beta \alpha }, \\ -L_{\beta }^{\prime }\circ (K_{\beta }^{-})^{-1} \circ K_{\alpha }(x)&{} \text { if } y=0 \text { and } x>\xi _{\alpha }^{+},\\ -L_{\beta }^{\prime }(-y) &{} \text { if } x=0 \text { and } y>-\xi _{\beta }^{-}. \end{array}\right. \end{aligned}$$

(5.14)

Proof

We compute the partial derivatives in domains where the function is naturally of class $C^{1}$ using that the function $\tau$ is continuously differentiable in $(0,1)^{2}$ and using (5.8). We prove the continuity of the partial derivatives using the same proof as Lemma 5.6. $\square$

5.4 Compatibility condition

In this subsection, we prove a compatibility result, which will be used in deriving error estimates. Let us recall the following shorthand notation

$$\begin{aligned} H(x,p)=\left\{ \begin{array}{l@{\quad }l} H_{\alpha }(p) &{} \text{ if } x\in J_{\alpha }^{\star } \\ F_{A}(\mathbf p ) &{} \text{ if } x=0. \end{array}\right. \end{aligned}$$

Fig. 2

Subsets of $\mathcal {D}_{0}$ for $\alpha = \beta$

Remark 5

In $J_{\alpha }\times J_{\alpha }$, we give a description of $\{\mathcal {D}_{{ junction}}(y,x)=L_{\alpha }(x-y)\}\cap \Delta _{\alpha \alpha }$ using [26], see Fig. 2. We have

$$\begin{aligned} \left\{ \begin{array}{ll} \mathcal {D}_{{ junction}}(0,\xi _{\alpha }^{+})=\xi _{\alpha }^{+} L_{\alpha }^{\prime }(\xi _{\alpha }^{+})+\tilde{L}_{A}(p) =L_{\alpha }(\xi _{\alpha }^{+}),\\ \mathcal {D}_{{ junction}}(-\xi _{\alpha }^{-},0)=\xi _{\alpha }^{-} L_{\alpha }^{\prime }(\xi _{\alpha }^{-})+\tilde{L}_{A}(p) =L_{\alpha }(\xi _{\alpha }^{-}). \end{array}\right. \end{aligned}$$

This means that the functions $\mathcal {D}_{{ junction}}$ and $(y,x)\rightarrow L_{\alpha }(x-y)$ coincide at the same points $X_{\alpha }=(0,\xi _{\alpha }^{+})$ and $Y_{\alpha }=(-\xi _{\alpha }^{-},0).$ Therefore we have

$$\begin{aligned} L_{\alpha }(x-y)<\mathcal {D}_{{ junction}}(y,x)\quad \text { on the open line segment } ]X_{\alpha },Y_{\alpha }[ \end{aligned}$$

because $\mathcal {D}_{{ junction}}$ is linear and $L_{\alpha }$ is strictly convex as a function of $y-x.$

The function $(y,x)\mapsto L_{\alpha }(x-y)-\mathcal {D}_{{ junction}}(y,x)$ being convex because $\mathcal {D}_{{ junction}}(y,x)$ is linear, we can consider the convex set

$$\begin{aligned} K^{\alpha }=\{(y,x)\in J_{\alpha }\times J_{\alpha }, \quad L_{\alpha }(x-y)\le \mathcal {D}_{{ junction}}(y,x)\}. \end{aligned}$$

Then the set

$$\begin{aligned} \Gamma ^{\alpha }=\{(y,x)\in \Delta _{\alpha \alpha },\quad \mathcal {D}_{{ junction}}(y,x)=L_{\alpha }(x-y)\} \end{aligned}$$

is contained in the boundary of the convex set $K^{\alpha }.$ More precisely, we have

$$\begin{aligned} \Gamma ^{\alpha }=((\partial K^{\alpha })\cap \Delta _{\alpha \alpha })\subset J_{\alpha }\times J_{\alpha } \end{aligned}$$

which shows that $\Gamma ^{\alpha }$ is a curve which contains the points $X_{\alpha }$ and $Y_{\alpha }$.

Theorem 5.8

Assume the Hamiltonians are convex, with Legendre Fenchel transform satisfying (B0). Then for all $(x,y)\in J\times J \backslash \bigcup \limits _{\alpha \in \{1,\dots , N \}} \Gamma ^{\alpha },$ (i.e., everywhere except on the curves where $\mathcal {D}_{0}$ is not $C^{1}$), we have

$$\begin{aligned} H(y,-\partial _{y}\mathcal {D}_{0}(y,x)) =H(x,\partial _{x}\mathcal {D}_{0}(y,x)). \end{aligned}$$

Proof of Theorem 5.8

First, notice that in the interior of $K^{\alpha }$ (i.e., in the regions where $\mathcal {D}_{0}(y,x)=L_{\alpha }(x-y)$), we have the result as

$$\begin{aligned} H(y,-\partial _{y}\mathcal {D}_{0}(y,x))=H_{\alpha }(L'_{\alpha }(x-y)) =H(x,\partial _{x}\mathcal {D}_{0}(y,x)). \end{aligned}$$

Now we prove the result in the regions where $\mathcal {D}_{0}=\mathcal {D}_{{ junction}}$. We distinguish different regions of $J_{\beta }\times J_{\alpha },$ defined in the expressions of $\partial _{x}\mathcal {D}_{{ junction}}$ and $\partial _{y}\mathcal {D}_{{ junction}}$ in (5.13)–(5.14). Let us first point out that we have the following assertion

$$\begin{aligned} H_{\alpha }(p)+L_{\alpha }(q)=pq \Leftrightarrow q\in \partial H_{\alpha }(p), \end{aligned}$$

(5.15)

where $\partial H_{\alpha }(p)$ is the convex subdifferential of $H_{\alpha }(p).$

We distinguish several cases.

Case 1$(y,x)\in (J_{\beta }^{\star }\times J_{\alpha }^{\star }){\setminus } \Delta _{\beta \alpha }$. From (5.15), on one hand, and from (5.14) we have

$$\begin{aligned} H_{\beta }\left( L_{\beta }^{\prime }\left( \frac{-y}{\tau }\right) \right) =\frac{-y}{\tau }L_{\beta }^{\prime }\left( \frac{-y}{\tau }\right) -L_{\beta }\left( \frac{-y}{\tau }\right) . \end{aligned}$$

From (5.5), we have then $H_{\beta } \left( L_{\beta }^{\prime }\left( \frac{-y}{\tau } \right) \right) =-K_{\beta }\left( \frac{-y}{\tau } \right) -\tilde{L}_{A}(p).$

On the other hand, and from (5.13)

$$\begin{aligned} H_{\alpha }\left( L_{\alpha }^{\prime }\left( \frac{x}{1-\tau }\right) \right) =\frac{x}{1-\tau }L_{\alpha }^{\prime }\left( \frac{x}{1-\tau }\right) -L_{\alpha }\left( \frac{x}{1-\tau }\right) , \end{aligned}$$

similarly, from (5.5), we deduce that $H_{\alpha }\left( L_{\alpha }^{\prime }\left( \frac{x}{1-\tau } \right) \right) =-K_{\alpha }\left( \frac{x}{1-\tau }\right) -\tilde{L}_{A}(p).$ Hence, from (5.8), the compatibility condition.

Case 2$(y,x)\in (J_{\beta }^{\star }\times J_{\alpha }^{\star })\cap \Delta _{\beta \alpha }.$ We argue as in Case 1, one can deduce that

$$\begin{aligned} H_{\beta }(L_{\beta }^{\prime }(\xi _{\beta }^{-}))= & {} -K_{\beta }(\xi _{\beta }^{-})-\tilde{L}_{A}(p)=A\\ H_{\alpha }(L_{\alpha }^{\prime }(\xi _{\alpha }^{+}))= & {} -K_{\alpha }(\xi _{\alpha }^{+})-\tilde{L}_{A}(p)=A \end{aligned}$$

From the definition of $\xi _{\alpha }^{+}$ and $\xi _{\beta }^{-},$ one can deduce the compatibility condition.

Remark 6

We deduce that the functions $\pi _{\alpha }^{+}, \pi _{\beta }^{-}$ defined in [25] satisfy

$$\begin{aligned} \pi _{\alpha }^{+}(A)=L_{\alpha }^{\prime }(\xi _{\alpha }^{+})\quad \text{ and } \quad \pi _{\beta }^{-}(A)=L'_{\beta }(\xi _{\beta }^{-}). \end{aligned}$$

Case 3$y=0$and$x> \xi _{\alpha }^{+}.$ Let us check the following equality

$$\begin{aligned} \max \left( A,\max _{\begin{array}{c} \beta =1,\dots ,N \end{array}} H_{\beta }^{-} \left( L_{\beta }^{\prime }\left( \left( K_{\beta }^{-}\right) ^{-1} \circ K_{\alpha }(x)\right) \right) \right) =H_{\alpha } \left( L_{\alpha }^{\prime }(x)\right) . \end{aligned}$$

On one hand, from the definition of $K_{\beta }^{-},$ we deduce that

$$\begin{aligned} H_{\beta }^{-}\left( L_{\beta }^{\prime }\left( \left( K_{\beta }^{-}\right) ^{-1} \circ K_{\alpha }(x)\right) \right) =H_{\beta }\left( L_{\beta }^{\prime } \left( \left( K_{\beta }^{-}\right) ^{-1}\circ K_{\alpha }(x)\right) \right) , \end{aligned}$$

and arguing as previously, we deduce that

$$\begin{aligned} H_{\beta }\left( L_{\beta }^{\prime }\left( \left( K_{\beta }^{-}\right) ^{-1} \circ K_{\alpha }(x)\right) \right)= & {} -K_{\beta } \left( \left( K_{\beta }^{-}\right) ^{-1}\circ K_{\alpha }(x)\right) -\tilde{L}_{A}(p)\\= & {} -K_{\alpha }(x)-\tilde{L}_{A}(p). \end{aligned}$$

On the other hand from (5.15), we have $H_{\alpha }(L_{\alpha }^{\prime }(x))=-K_{\alpha }(x)-\tilde{L}_{A}(p).$

And for $x>\xi _{\alpha }^{+},$ we have $H_{\alpha }(L_{\alpha }^{\prime }(x))> H_{\alpha }(L_{\alpha }^{\prime }(\xi _{\alpha }^{+})) =H_{\alpha }(\pi _{\alpha }^{+}(A))=A.$ So one can deduce the compatibility condition.

Case 4$x=0$and$y> -\xi _{\beta }^{-}$ Let us check the following equality

$$\begin{aligned}&\max \left( A,\max \limits _{\begin{array}{c} \alpha =1,\dots ,N\\ \alpha \ne \beta \end{array}}H_{\alpha }^{-}\left( L_{\alpha }^{\prime } \left( \left( K_{\alpha }^{+}\right) ^{-1}\circ K_{\beta }(-y)\right) \right) , H_{\beta }^{-}\left( L_{\beta }^{\prime }(-y)\right) \right) \\&\quad =H_{\beta } \left( L_{\beta }^{\prime }(-y)\right) . \end{aligned}$$

Similarly, as in the previous case, one can deduce that

$$\begin{aligned} \max \limits _{\begin{array}{c} \alpha =1,\dots ,N\\ \alpha \ne \beta \end{array}} H_{\alpha }^{-}\left( L_{\alpha }^{\prime } \left( \left( K_{\alpha }^{+}\right) ^{-1} \circ K_{\beta }(-y)\right) \right) =A_{0}\le A. \end{aligned}$$

And for $y>\xi _{\beta }^{-},$ we have $H_{\beta }^{-}(L_{\beta }^{\prime }(-y))> H_{\beta }^{-}(\pi _{\beta }^{-}(A))=A.$

Case 5$y=0$and$0<x\le \xi _{\alpha }^{+}$ Let us check the following equality

$$\begin{aligned} \max (A,\max _{\begin{array}{c} \beta =1,\dots ,N \end{array}} H_{\beta }^{-}(L_{\beta }^{\prime }(\xi _{\beta }^{-}))) =H_{\alpha }(L_{\alpha }^{\prime }(\xi _{\alpha }^{+})). \end{aligned}$$

On one hand, from (5.15) $H_{\alpha }(L_{\alpha }^{\prime } (\xi _{\alpha }^{+}))=-K_{\alpha }(\xi _{\alpha }^{+})-\tilde{L}_{A}(p) =-\tilde{L}_{A}(p)=A.$

On the other hand, $\max \nolimits _{\beta =1,\dots ,N} H_{\beta }^{-}(L_{\beta }^{\prime }(\xi _{\beta }^{-}))= \max \nolimits _{\beta =1,\dots ,N} H_{\beta }^{-}(L_{\beta }^{\prime }(\xi _{\beta }^{-}))= \max \nolimits _{\beta =1,\dots ,N} H_{\beta }^{-}(\pi _{\beta }^{-}(A))=A.$

Case 6$x=0$and$0<y\le -\xi _{\beta }^{-}$ Let us check the following equality

$$\begin{aligned} \max (A,\max _{\begin{array}{c} \alpha =1,\dots ,N \end{array}} H_{\alpha }^{-}(L_{\alpha }^{\prime }(\xi _{\alpha }^{+})) =H_{\beta }(L_{\beta }^{\prime }(\xi _{\beta }^{-})). \end{aligned}$$

Similarly, as in Case 5, one can deduce the compatibility condition.

Case 7$x=0$and$y=0$ Let us check the following equality

$$\begin{aligned} \max (A,\max _{\begin{array}{c} \beta =1,\dots ,N \end{array}} H_{\beta }^{-}(L_{\beta }^{\prime }(\xi _{\beta }^{-})) =\max (A,\max _{\begin{array}{c} \alpha =1,\dots ,N \end{array}} H_{\alpha }^{-}(L_{\alpha }^{\prime }(\xi _{\alpha }^{+})). \end{aligned}$$

In fact, it follows directly from Cases 5 and 6.

The proof is thus complete. $\square$

5.5 $C^{1,1}$ estimates for the reduced minimal action

In this section, we study the Lipschitz regularity of the gradient of the reduced minimal action $\mathcal {D}_{0}$. It turns out that its gradient is indeed Lipschitz if the flux limiter A is not equal to $A_0$, the minimal flux limiter. Such a technical result will be used when deriving error estimates. It is also of independent interest.

Proposition 5.9

($C^{1,1}$ estimates for the reduced minimal action) Let $\rho >0$ and assume that the Hamiltonians satisfy (1.10) and (1.9). The function $\mathcal {D}_{0}$ associated with the flux limiter $A_0+\rho$ can be chosen $C^{1,1}(J_{K}^2)$ for any $K>0$ where $J_{K}^2=\{(x,y)\in J^2: d(0,x)\le K \text{ and } d(0,y)\le K \}$. Moreover, there exist $C_K$ and $C'_K$ such that

$$\begin{aligned} ||{ \partial _{xx}\mathcal {D}_{{ junction}}}||_{L^{\infty }(J^2_K)}\le \frac{C_K}{\min (1,\rho )}; \end{aligned}$$

(5.16)

and

$$\begin{aligned} ||H'_{\alpha }(\partial _{x}\mathcal {D}_{{ junction}}) \partial _{xx}\mathcal {D}_{{ junction}}||_{L^{\infty }(J^2_K)} \le \frac{C'_K}{\min (1,\sqrt{\rho })}. \end{aligned}$$

(5.17)

the constants $C_K$ and $C'_K$ depend only on K and (1.10).

Moreover, in the case where for all $\alpha \in \{1, \ldots , N \}$, $\min H_{\alpha }=A_{0}$, we have

$$\begin{aligned} ||{ \partial _{xx}\mathcal {D}_{{ junction}}}||_{L^{\infty }(J^2_K)}\le C_K. \end{aligned}$$

(5.18)

Proof

In the following A denotes $A_0+\rho$. Using (5.13), we see that $\partial _{xx}\mathcal {D}_{{ junction}}=0$ on $\Delta _{\beta \alpha }$ for all $(\beta ,\alpha )\in \{1,\dots , N\}^{2}$ and $\partial _{xx}\mathcal {D}_{{ junction}}(y,x) =L_{\alpha }^{''}(x)$ on $\{0\}\times \{x\in J_{\alpha } \ | \ x>\xi _{\alpha }^{+}\}$. So it is sufficient to prove (5.16) and (5.17) on $T:=J_{\beta }^{\star }\times J_{\alpha }^{\star } \backslash \Delta _{\beta \alpha }$ for all $(\beta ,\alpha )\in \{1,\dots ,N\}^{2}$. By (5.13), we deduce that on T,

$$\begin{aligned} \partial _{xx}\mathcal {D}_{{ junction}}(y,x)=\left( \frac{1}{1-\tau (y,x)} +\frac{x}{(1-\tau (y,x))^2}\frac{\partial \tau }{\partial x}(y,x)\right) L_{\alpha }^{\prime \prime }\left( \frac{x}{1-\tau (y,x)}\right) . \end{aligned}$$

Let us compute also $\frac{\partial \tau }{\partial x}$ using (5.8),

$$\begin{aligned} \frac{\partial \tau }{\partial x}(y,x) =\frac{\frac{1}{1-\tau (y,x)} K_{\alpha }^{\prime } \left( \frac{x}{1-\tau (y,x)}\right) }{\frac{y}{\tau (y,x)^{2}} K_{\beta }^{\prime }\left( \frac{-y}{\tau (y,x)}\right) -\frac{x}{(1-\tau (y,x))^{2}}K_{\alpha }^{\prime } \left( \frac{x}{1-\tau (y,x)}\right) }. \end{aligned}$$

And as $K_{\beta }^{\prime }\left( \frac{-y}{\tau }\right) =\frac{y}{\tau }L_{\beta }^{\prime \prime }\left( \frac{-y}{\tau }\right) \ge 0$ and $K_{\alpha }^{\prime }\left( \frac{x}{1-\tau }\right) =\frac{-x}{1-\tau }L_{\alpha }^{\prime \prime }\left( \frac{x}{1-\tau }\right) \le 0$ we deduce that

$$\begin{aligned} \frac{\partial \tau }{\partial x}(y,x) = \frac{\frac{-x}{(1-\tau (y,x))^{2}}L_{\alpha }^{\prime \prime } \left( \frac{x}{1-\tau (y,x)}\right) }{\frac{y^2}{\tau (y,x)^{3}} L_{\beta }^{\prime \prime }\left( \frac{-y}{\tau (y,x)}\right) +\frac{x^2}{(1-\tau (y,x))^{3}}L_{\alpha }^{\prime \prime } \left( \frac{x}{1-\tau (y,x)}\right) }. \end{aligned}$$

(5.19)

So we have on T

$$\begin{aligned} \partial _{xx}\mathcal {D}_{{ junction}}(y,x) =\frac{\frac{y^2}{(1-\tau (y,x))\tau (y,x)^{3}} L_{\alpha }^{\prime \prime }\left( \frac{x}{1-\tau (y,x)}\right) L_{\beta }^{\prime \prime }\left( \frac{-y}{\tau (y,x)}\right) }{\frac{y^2}{\tau (y,x)^{3}}L_{\beta }^{\prime \prime } \left( \frac{-y}{\tau (y,x)}\right) +\frac{x^2}{(1-\tau (y,x))^{3}} L_{\alpha }^{\prime \prime }\left( \frac{x}{1-\tau (y,x)}\right) } \ge 0. \end{aligned}$$

(5.20)

As the denominator is a sum of two positive functions, $\partial _{xx}\mathcal {D}_{{ junction}}$ from above by the same numerator over only one term of the denominator. We deduce in these two cases that,

$$\begin{aligned} \partial _{xx}\mathcal {D}_{{ junction}}(y,x) \le \left\{ \begin{array}{l@{\quad }l} 2L_{\alpha }^{\prime \prime }\left( \frac{x}{1-\tau (y,x)}\right) &{} \text{ if } \tau (y,x)\le \frac{1}{2}\\ \frac{8y^{2}}{\left( \frac{x}{1-\tau (y,x)}\right) ^{2}} L_{\beta }^{\prime \prime }\left( \frac{-y}{\tau (y,x)}\right) &{} \text{ if } \tau (y,x)\ge \frac{1}{2}. \end{array}\right. \end{aligned}$$

(5.21)

Moreover, we have on T,

$$\begin{aligned} H_{\alpha }^{\prime }\left( \partial _{x} \mathcal {D}_{{ junction}}(y,x) \right) =H_{\alpha }^{\prime } \left( L_{\alpha }^{\prime }\left( \frac{x}{1-\tau (y,x)}\right) \right) =\frac{x}{1-\tau (y,x)}, \end{aligned}$$

and

$$\begin{aligned} \frac{x}{1-\tau (y,x)}\partial _{xx}\mathcal {D}_{{ junction}}(y,x) \le \left\{ \begin{array}{l@{\quad }l} 4 x^{2}L_{\alpha }^{\prime \prime }\left( \frac{x}{1-\tau (y,x)}\right) &{} \text{ if } \tau (y,x)\le \frac{1}{2}\\ \frac{8y^{2}}{\frac{x}{1-\tau (y,x)}} L_{\beta }^{\prime \prime } \left( \frac{-y}{\tau (y,x)}\right) &{} \text{ if } \tau (y,x)\ge \frac{1}{2}. \end{array}\right. \end{aligned}$$

In the case $\tau (y,x)\le \frac{1}{2}$, as $0\le \frac{x}{1-\tau (y,x)}\le 2x$, we get the inequality (5.16) and (5.17). Let us prove the following lower bound for $(y,x)\in T$,

$$\begin{aligned} \frac{x}{1-\tau (y,x)}\ge \xi _{\alpha }^{+}, \end{aligned}$$

(5.22)

which helps us for the second case. For $y \in J_{\beta }$, we see that $x\rightarrow \frac{x}{1-\tau (y,x)}$ has a non-negative derivative using (5.19), so it is a non-decreasing function. Therefore to prove (5.22), it is sufficient to show it on $\partial T$. Let (y, x) be in $\partial T$. We distinguish three cases.

In the case where $y=0$, necessarily $x\ge \xi _{\alpha }^{+}$ and as $\tau (y,x)\in [0,1]$, we deduce (5.22).

In the case where $y\in ]0,-\xi _{\beta }^{-}[$, we have $(y,x) \in \bigg \{(y,x)\in J_{\beta }\times J_{\alpha }, \quad \frac{x}{\xi _{\alpha }^{+}}-\frac{y}{\xi _{\beta }^{-}}= 1 \bigg \}$. So by (5.10) we deduce that $\frac{x}{1-\tau (y,x)}=\xi _{\alpha }^{+}$.

In the case where $y\ge -\xi _{\beta }^{-}$, we have $x=0$. It is enough to prove that

$$\begin{aligned} \liminf \limits _{x'\rightarrow 0} \frac{x'}{1-\tau (y,x')} \ge \xi _{\alpha }^{+}. \end{aligned}$$

(5.23)

We have for $(y,x') \in T$,

$$\begin{aligned} K_{\alpha }\left( \frac{x'}{1-\tau (y,x')}\right) =K_{\beta }\left( \frac{-y}{\tau (y,x')} \right) \le K_{\beta }\left( \frac{-\xi _{\beta }^{-}}{\tau (y,x')} \right) , \end{aligned}$$

as $K_{\beta }$ is non-decreasing on $]-\infty ,0]$. We deduce that

$$\begin{aligned} \frac{x'}{1-\tau (y,x')}\ge (K_{\alpha }^{+})^{-1}\circ K_{\beta }\left( \frac{-\xi _{\beta }^{-}}{\tau (y,x')} \right) , \end{aligned}$$

as $(K_{\alpha }^{+})^{-1}$ is non-increasing. As $\lim \limits _{x'\rightarrow 0}\tau (y,x')=1$, taking the limit inferior in the preceding inequality gives (5.23). So we deduce (5.22) and

$$\begin{aligned} \partial _{xx}\mathcal {D}_{{ junction}}(y,x)\le & {} \frac{8y^{2}}{(\xi _{\alpha }^{+})^{2}} L_{\beta }^{\prime \prime } \left( \frac{-y}{\tau (y,x)}\right) \quad \text{ if } \tau (y,x) \ge \frac{1}{2},\\ \frac{x}{1-\tau (y,x)}\partial _{xx}\mathcal {D}_{{ junction}}(y,x)\le & {} \frac{8y^{2}}{\xi _{\alpha }^{+}} L_{\beta }^{\prime \prime } \left( \frac{-y}{\tau (y,x)}\right) \quad \text{ if } \tau (y,x) \ge \frac{1}{2}. \end{aligned}$$

If $\xi _{\alpha }^{+}>1$, we deduce (5.16). If $\xi _{\alpha }^{+}\le 1$, let us prove that it exists a constant $C>0$ only depending on (1.10) such that

$$\begin{aligned} (\xi _{\alpha }^{+})^{2}\ge C\rho . \end{aligned}$$

(5.24)

As $A=A_{0}+\rho$ we have

$$\begin{aligned} K_{\alpha }(\xi )=L_{\alpha }(\xi )-\xi L_{\alpha }^{\prime }(\xi )+A_{0}+\rho , \end{aligned}$$

and

$$\begin{aligned} K_{\alpha }^{\prime }(\xi )=-\xi L_{\alpha }^{\prime \prime }(\xi ). \end{aligned}$$

The function $L_{\alpha }^{\prime \prime }$ is bounded on [0, 1], it exists $M>0$ such that

$$\begin{aligned} \gamma \le L_{\alpha }^{\prime \prime } \le M. \end{aligned}$$

So we have $K_{\alpha }^{\prime }(\xi )\ge -M\xi$. We integrate from 0 to $\xi \ge 0$ and get

$$\begin{aligned} K_{\alpha }(\xi )-K_{\alpha }(0)\ge -M\frac{\xi ^{2}}{2}. \end{aligned}$$

(5.25)

Taking $\xi =\xi _{\alpha }^{+}$, as $K_{\alpha }(\xi _{\alpha }^{+})=0$ and as $L_{\alpha }(0)+A_{0}\ge 0$, we deduce that

$$\begin{aligned} (\xi _{\alpha }^{+})^{2}\ge \frac{2}{M}(L_{\alpha }(0)+A_{0}+\rho ) \ge \frac{2}{M}\rho . \end{aligned}$$

So we get (5.24) and we deduce (5.16) and (5.17).

In the case where for all $\alpha \in \{1, \ldots , N \}$, $\min H_{\alpha }=A_{0}$, we only have to consider the case $\tau (y,x)\ge \frac{1}{2}$ in (5.21) since the case $\tau (y,x)\le \frac{1}{2}$ gives already the bound (5.21). In order to get a bound for the term $\frac{8y^{2}}{\left( \frac{x}{1-\tau (y,x)} \right) ^{2}}=\frac{8y^{2}}{\left( (K_{\alpha }^{+})^{-1}\circ K_{\beta }\left( -\frac{y}{\tau (y,x)}\right) \right) ^{2}}$, let us prove that for all $\xi \in [-2K,2K]$, we have

$$\begin{aligned} \frac{\xi ^{2}}{\left( (K_{\alpha }^{+})^{-1} \circ K_{\beta }(-\xi )\right) ^{2}} \le C_{2K}, \end{aligned}$$

(5.26)

where $C_{2K}>0$ is a constant which depends on K. Let $M_{2K}$ be such that on $[-2K,2K]$ we have for all $\alpha \in \{1, \ldots , N \}$,

$$\begin{aligned} \gamma \le L_{\alpha }^{\prime \prime } \le M_{2K}. \end{aligned}$$

Replacing $\xi$ by $(K_{\alpha }^{+})^{-1}(\xi )$ in (5.25), we deduce that

$$\begin{aligned} M_{2K} \frac{\left( (K_{\alpha }^{+})^{-1}(\xi )\right) ^{2}}{2} \ge -\xi +K_{\alpha }(0). \end{aligned}$$

So we have

$$\begin{aligned} M_{2K} \frac{\left( (K_{\alpha }^{+})^{-1}\circ K_{\beta }(-\xi )\right) ^{2}}{2}\ge -K_{\beta }(-\xi )+K_{\alpha }(0). \end{aligned}$$

As for (5.25), we have the following inequality

$$\begin{aligned} K_{\beta }(0)-K_{\beta }(-\xi )\ge \gamma \frac{\xi ^{2}}{2}. \end{aligned}$$

So as $K_{\alpha }(0)=K_{\beta }(0)=\rho$ we deduce that

$$\begin{aligned} M_{2K} \frac{\left( (K_{\alpha }^{+})^{-1}\circ K_{\beta }(-\xi )\right) ^{2}}{2}\ge \gamma \frac{\xi ^{2}}{2}+K_{\alpha }(0)-K_{\beta }(0) \ge \gamma \frac{\xi ^{2}}{2}. \end{aligned}$$

That gives (5.26) and we deduce (5.18). $\square$

6 Error estimates

6.1 Proof of the error estimates

To prove Theorem 1.2, we will need the following result whose classical proof is given in “Appendix” for the reader’s convenience.

Lemma 6.1

(A priori control) Let $T>0$ and let $u^h$ be a discrete sub-solution of the numerical scheme (1.16)–(1.18) and u a super-solution of (1.1)–(1.2) satisfying for some $C_T>0$,

$$\begin{aligned} u(t,x)\ge -C_{T}(1+d(0,x))\qquad \text { for } \quad t\in (0,T). \end{aligned}$$

Then there exists a constant $C=C(T)>0$ such that for all $(t,x) \in \mathcal {G}_h$, $t \le T$, and $(s,y)\in [0,T)\times J$, we have

$$\begin{aligned} u^h(t,x)\le u(s,y)+C(1+d(x,y)). \end{aligned}$$

(6.1)

We also need the following result [25, Lemma 4.4] where the proof is given in [25].

Lemma 6.2

(From quasi-convex to convex Hamiltonians) Let $K\in (0,+\,\infty ).$ Given Hamiltonians $H_{\alpha }:[-K,K]\rightarrow \mathbb {R}$ satisfying (1.4), there exists a function $\chi :\mathbb {R}\rightarrow \mathbb {R}$ such that the functions $\chi \circ H_{\alpha }$ satisfy (1.10) for $\alpha =1,\ldots ,N$. Moreover, we can choose $\chi$ such that $\chi \in C^{2}(\mathbb {R})$ and $\chi '>1$.

Remark 7

In [25, Lemma 4.4], the functions $\chi \circ H_{\alpha }$ satisfy in fact the following assumptions

$$\begin{aligned} \left\{ \begin{array}{l} H_{\alpha }\in C^{2}(\mathbb {R}) \text { with } H''_{\alpha }>0 \text { on } \mathbb {R},\\ H'_{\alpha }<0 \text { on } (-\infty ,0) \text { and } H'_{\alpha }>0 \text { on } (0,+\,\infty ),\\ \lim \nolimits _{|p|\rightarrow +\,\infty } \frac{H_{\alpha }(p)}{|p|}= +\,\infty . \end{array}\right. \end{aligned}$$

(6.2)

which implies (1.10). Indeed, in the next proof on error estimates, we only need to consider Hamiltonians on a compact set which only depends on $u_{0}$ and the Hamiltonians $H_{\alpha }$, thanks to the fact that the solution is Lipschitz continuous, see Theorem 2.3 and (3.2). So on $[-K,K]$, the functions $(\chi \circ H_{\alpha })''$ are bounded by some constant $C>0$. We deduce that the functions $L_{\alpha }$ are of class $C^{2}$ and satisfy $L''_{\alpha }\ge \gamma =\frac{1}{C}$. Indeed, from the relation $H_{\alpha }(p)+L_{\alpha }(q)=pq$ with $q=H'_{\alpha }(p)$, one can deduce that $L'_{\alpha }(H'_{\alpha }(q))=q,$ so

$$\begin{aligned} L''_{\alpha }(q)=\frac{1}{H''_{\alpha }\circ (H'_{\alpha })^{-1}(q)} \ge \gamma . \end{aligned}$$

We now turn to the proof of the error estimates in the case of flux-limited junction conditions.

Proof of Theorem 1.2

We assume that the Hamiltonians $H_{\alpha }$ satisfy (1.4). Let u be the solution of (1.6) and $u^{h}$ the solution of the corresponding scheme (1.16) with $F=F_{A}$.

In order to get (1.23), we only prove that

$$\begin{aligned} u^h(t,x)-u(t,x)\le {\left\{ \begin{array}{ll} C_T (\Delta x)^{1/2} &{} \text { if } A>A_0, \\ C_T (\Delta x)^{2/5} &{} \text { if } A=A_0 \end{array}\right. } \qquad \text { in } [0,T)\times {J} \cap \mathcal {G}_{h} \end{aligned}$$

since the proof of the other inequality is very similar. We are going to prove that

$$\begin{aligned}&u^{h}(t,x)-u(t,x)\nonumber \\&\quad \le {\left\{ \begin{array}{ll} \mathcal {O} \left( \frac{\Delta t}{\nu }\right) + \mathcal {O}\left( \frac{\Delta x}{\varepsilon }\right) +\mathcal {O}(\varepsilon )+\mathcal {O}(\nu ) &{} \text { if } A > A_0, \\ \mathcal {O} \left( \frac{\Delta t}{\nu }\right) + \mathcal {O} \left( \frac{\Delta x}{\varepsilon \sqrt{\rho }}\right) + \mathcal {O}\left( \frac{(\Delta x)^2}{(\varepsilon \rho )^2}\right) +\mathcal {O}(\rho ) +\mathcal {O}(\varepsilon )+\mathcal {O}(\nu ) &{} \text { if } A = A_0. \end{array}\right. } \end{aligned}$$

(6.3)

which yields the desired inequality by minimizing the right hand side with respect to $\varepsilon$ and $\nu$ in the case $A>A_0$ and with respect to $\rho , \varepsilon$ and $\nu$ in the case $A=A_0$. Let $\chi$ be the function defined in Lemma 6.2 such that the functions $\chi \circ H_{\alpha }$ satisfy (1.10). In the following, we consider that the function $\mathcal {D}_{0}$ is associated to the Hamiltonians $\chi \circ H_{\alpha }$ and to the flux limiter $\chi (A)$ which satisfies $\chi (A) >\chi (A_{0})$ in the case $A>A_{0}$.

The remaining of the proof proceeds in several steps.

Step 1: Penalization procedure Using the expression of $\mathcal {D}_{0}$ in (5.2) and $\mathcal {D}_{{ junction}}$ in (5.6), we deduce that it exists $C>0$, such that $\forall x \in J$

$$\begin{aligned} \mathcal {D}_{0}(0,0)=\tilde{L}_{A}(p) =-A\le \mathcal {D}_{0}(x,x)\le C. \end{aligned}$$

Let $\tilde{\mathcal {D}}_{0}=\mathcal {D}_{0}+A$, we have that

$$\begin{aligned} 0 \le \tilde{\mathcal {D}}_{0}(x,x)\le C+A. \end{aligned}$$

For $\eta$, $\delta$, $\varepsilon$, $\nu$ positive constants, let us define

$$\begin{aligned} M_{\varepsilon ,\delta }=\sup _{\begin{array}{c} {(t,x)\in \mathcal {G}_h},\\ {(s,y)\in [0,T)\times J} \end{array}} \bigg \{u^h(t,x)-u(s,y)-\varepsilon \tilde{\mathcal {D}}_{0}\left( \frac{y}{\varepsilon }, \frac{x}{\varepsilon }\right) -\frac{(t-s)^2}{2\nu } -\frac{\delta }{2}d^2(y,0)-\frac{\eta }{T-s}\bigg \} \end{aligned}$$

(6.4)

where the test function $\mathcal {D}_0$ is given in (5.2). In this step, we assume that $M_{\varepsilon ,\delta }>0.$ Thanks to Lemma 6.1 and the superlinearity of $\mathcal {D}_0$ (see Lemma 5.2), we deduce that for (x, y) such that the quantity in the supremum is larger than $\frac{M_{\varepsilon ,\delta }}{2}$, we have

$$\begin{aligned} 0<\frac{M_{\varepsilon ,\delta }}{2}\le C(1+d(y,x)) -\varepsilon \frac{\gamma }{2}d^2\left( \frac{y}{\varepsilon }, \frac{x}{\varepsilon }\right) -\frac{(t-s)^2}{2\nu } -\frac{\delta }{2}d^2(y,0)-\frac{\eta }{T-s} \end{aligned}$$

which implies in particular

$$\begin{aligned} \frac{\gamma }{2\varepsilon }d^2(y,x)\le C(1+d(y,x)), \end{aligned}$$

and

$$\begin{aligned} \frac{\delta }{2}d^2(y,0)\le C(1+d(y,x)). \end{aligned}$$

Notice that in the following, we use the notation $\mathcal {D}_{0}$ instead of $\tilde{\mathcal {D}}_{0}$. Indeed we deal only with partial derivatives of $\mathcal {D}_{0}$ which are equal to partial derivatives of $\tilde{\mathcal {D}}_{0}$ and differences between two values of $\mathcal {D}_{0}$ at two points which are equal to differences between two values of $\tilde{\mathcal {D}}_{0}$ at these two points.

We deduce from the two last inequalities that d(y, x) is bounded and d(y, 0) is bounded, so the supremum is reached at some point (t, x, s, y) where $y\in J_{\beta }$ and $x \in J_{\alpha }$. This estimate together with the fact that $-\partial _{y}\mathcal {D}_{0} (\frac{y}{\varepsilon },\frac{x}{\varepsilon })- \delta d(y,0)$ lies in the viscosity subdifferential of $u(t,\cdot )$ at x and the fact that $\delta d(y,0)$ is bounded, implies that there exists $K>0$ only depending on $\Vert \nabla u\Vert _\infty$ (see Theorem 2.3) such that the point (t, x, s, y) realizing the maximum satisfies

$$\begin{aligned} \left| \partial _{y}\mathcal {D}_{0} \left( \frac{y}{\varepsilon }, \frac{x}{\varepsilon }\right) \right| \le K. \end{aligned}$$

(6.5)

If $\alpha = \beta ,$ for $\frac{y}{\varepsilon }$ or $\frac{x}{\varepsilon }$ large, then (6.5) implies

$$\begin{aligned} \left| L_{\alpha }^{\prime }\left( \frac{y}{\varepsilon } -\frac{x}{\varepsilon }\right) \right| \le K. \end{aligned}$$

As $L_{\alpha }$ is superlinear, it implies that $d\left( \frac{y}{\varepsilon },\frac{x}{\varepsilon }\right) \le C$, for $C>0$ which is sufficient for the use in step 2 of the $C^{1,1}$ estimates as $\mathcal {D}_{0}$ only depends on $d\left( \frac{y}{\varepsilon },\frac{x}{\varepsilon }\right)$ for $\frac{y}{\varepsilon }$ or $\frac{x}{\varepsilon }$ large. If $\alpha \ne \beta$, assume by contradiction that $\frac{y}{\varepsilon }$ or $\frac{x}{\varepsilon }$ are not bounded when $\varepsilon \rightarrow 0$. Then using (5.8) and (5.14) we get a contradiction with (6.5). So $\frac{y}{\varepsilon }$ and $\frac{x}{\varepsilon }$ are bounded by a constant which only depends on $\Vert \nabla u\Vert _\infty$ and the Hamiltonians $H_{\alpha }$.

We want to prove that for $\eta >\eta ^{\star }$ (to be determined) the supremum in (6.4) is attained for $t=0$ or $s=0.$ We assume that $t>0$ and $s>0$ and we prove that $\eta \le \eta ^{\star }$.

Step 2: Viscosity inequalities Since $t>0$ and $s>0$, we can use Lemma 4.3 and get the following viscosity inequalities.

If $x \ne 0$, then

$$\begin{aligned}&\frac{t-s}{\nu }-\frac{\Delta t}{2\nu } +\max \bigg \{ H_{\alpha }^{-} \left( \frac{\varepsilon }{\Delta x} \left\{ \mathcal {D}_0 \left( \frac{y}{\varepsilon }, \frac{x+\Delta x}{\varepsilon } \right) -\mathcal {D}_0\left( \frac{y}{\varepsilon },\frac{x}{\varepsilon }\right) \right\} \right) ,\\&\quad H_{\alpha }^{+} \bigg ( \frac{\varepsilon }{\Delta x} \bigg \{ \mathcal {D}_0\bigg (\frac{y}{\varepsilon },\frac{x}{\varepsilon }\bigg ) -\mathcal {D}_0\bigg (\frac{y}{\varepsilon },\frac{x-\Delta x}{\varepsilon }\bigg ) \bigg \}\bigg )\bigg \} \le 0. \end{aligned}$$

If $x =0$, then

$$\begin{aligned} \frac{t-s}{\nu }-\frac{\Delta t}{2\nu }+\max \bigg (A, \max _{\begin{array}{c} \beta \end{array}} \left\{ H_{\beta }^{-}\left( \frac{\varepsilon }{\Delta x}\bigg \{\mathcal {D}_0 \left( \frac{y}{\varepsilon },\frac{\Delta x}{\varepsilon }\right) -\mathcal {D}_0 \left( \frac{y}{\varepsilon },0\right) \bigg \}\right) \right\} \bigg )\le 0. \end{aligned}$$

If $y \ne 0$, then

$$\begin{aligned} -\frac{\eta }{(T-s)^2}+\frac{t-s}{\nu } +H_{\alpha } \left( -\partial _{y}{\mathcal {D}_0}\left( \frac{y}{\varepsilon }, \frac{x}{\varepsilon }\right) -\delta d(y,0)\right) \ge 0. \end{aligned}$$

If $y =0$, then

$$\begin{aligned} -\frac{\eta }{(T-s)^2}+\frac{t-s}{\nu }+ F_{A} \left( -\partial _{y}\mathcal {D}_0 \left( 0,\frac{x}{\varepsilon }\right) \right) \ge 0. \end{aligned}$$

We now distinguish the case $A>A_0$ and $A=A_0$.

Case$A>A_0$ Thanks to the $C^{1,1}$ regularity of the function $\mathcal {D}_0$, see Proposition 5.9, and the fact that the functions $H_{\alpha }^{\pm }, H_{\alpha }$ are locally Lipschitz

we obtain, for $x\in J_{\alpha }$ and $y\in J_{\beta }$ with $\alpha \ne \beta$ (i.e. for $\mathcal {D}_{0}=\mathcal {D}_{{ junction}}$),

$$\begin{aligned}&\text { if } x \ne 0, \qquad \frac{t-s}{\nu } -\frac{\Delta t}{2\nu }+H_{\alpha }\left( \partial _x \mathcal {D}_0 \left( \frac{y}{\varepsilon },\frac{x}{\varepsilon }\right) \right) +O\left( \frac{\Delta x}{\varepsilon }\right) \le 0 \end{aligned}$$

(6.6)

$$\begin{aligned}&\text { if } x = 0, \qquad \frac{t-s}{\nu }-\frac{\Delta t}{2\nu }+F_{A} \left( \partial _x\mathcal {D}_0\left( \frac{y}{\varepsilon },0\right) \right) +O\left( \frac{\Delta x}{\varepsilon }\right) \le 0 \end{aligned}$$

(6.7)

$$\begin{aligned}&\text { if } y \ne 0,\qquad \frac{t-s}{\nu } +H_{\beta } \left( -\partial _y \mathcal {D}_0\left( \frac{y}{\varepsilon }, \frac{x}{\varepsilon }\right) \right) +O(\sqrt{\delta }) \ge \frac{\eta }{2 T^2} \end{aligned}$$

(6.8)

$$\begin{aligned}&\text { if } y = 0, \qquad \frac{t-s}{\nu } +F_{A} \left( -\partial _y \mathcal {D}_0 \left( 0,\frac{x}{\varepsilon }\right) \right) \ge \frac{\eta }{2 T^2}. \end{aligned}$$

(6.9)

Now for $(y,x)\in J_{\alpha }\times J_{\alpha },$ from (5.2) and (5.6), one can deduce that $\mathcal {D}_0$ is in fact $C^2$ far away from the curve $\Gamma ^{\alpha }$ defined in Remark 5, hence the viscosity inequalities (6.6)–(6.9) remain true.

Now we treat the case where $(\frac{y}{\varepsilon },\frac{x}{\varepsilon })$ is near the curve $\Gamma ^{\alpha },$ but not on it.

First if $(\frac{y}{\varepsilon },\frac{x}{\varepsilon })$ is such that $(\frac{y}{\varepsilon },\frac{x}{\varepsilon })\in K^{\alpha }\backslash \Gamma ^{\alpha }$ and $(\frac{y}{\varepsilon },\frac{x-\Delta x}{\varepsilon })\notin K^{\alpha },$ we have

$$\begin{aligned} \mathcal {D}_0\left( \frac{y}{\varepsilon },\frac{x-\Delta x}{\varepsilon }\right) \le L_{\alpha }\left( \frac{x-\Delta x -y}{\varepsilon }\right) . \end{aligned}$$

So as $H_{\alpha }^{+}$ is non-decreasing, we deduce that

$$\begin{aligned}&H_{\alpha }^{+} \bigg ( \frac{\varepsilon }{\Delta x} \bigg \{L_{\alpha }\bigg (\frac{x-y}{\varepsilon }\bigg ) -L_{\alpha }\bigg (\frac{x-\Delta x-y}{\varepsilon }\bigg ) \bigg \}\bigg )\\&\quad \le H_{\alpha }^{+} \bigg ( \frac{\varepsilon }{\Delta x} \bigg \{\mathcal {D}_0\bigg (\frac{y}{\varepsilon },\frac{x}{\varepsilon }\bigg ) -\mathcal {D}_0\bigg (\frac{y}{\varepsilon }, \frac{x-\Delta x}{\varepsilon }\bigg ) \bigg \}\bigg ). \end{aligned}$$

Hence the viscosity inequalities (6.6)–(6.9) remain true. If $(\frac{y}{\varepsilon },\frac{x}{\varepsilon })$ is such that $(\frac{y}{\varepsilon },\frac{x}{\varepsilon })\notin K^{\alpha }$ and $(\frac{y}{\varepsilon },\frac{x+\Delta x}{\varepsilon })\in K^{\alpha }\backslash \Gamma ^{\alpha }$, we have

$$\begin{aligned} \mathcal {D}_0\left( \frac{y}{\varepsilon }, \frac{x+\Delta x}{\varepsilon }\right) \le \mathcal {D}_{{ junction}}\left( \frac{y}{\varepsilon }, \frac{x+\Delta x}{\varepsilon }\right) . \end{aligned}$$

So as $H_{\alpha }^{-}$ is non-increasing, we deduce that

$$\begin{aligned}&H_{\alpha }^{-} \bigg ( \frac{\varepsilon }{\Delta x} \bigg \{\mathcal {D}_{{ junction}}\bigg (\frac{y}{\varepsilon }, \frac{x+\Delta x}{\varepsilon }\bigg )-\mathcal {D}_{{ junction}} \bigg (\frac{y}{\varepsilon },\frac{x}{\varepsilon }\bigg )\bigg \}\bigg )\\&\quad \le H_{\alpha }^{-} \bigg ( \frac{\varepsilon }{\Delta x} \bigg \{ \mathcal {D}_0\bigg (\frac{y}{\varepsilon }, \frac{x+\Delta x}{\varepsilon }\bigg ) -\mathcal {D}_0\bigg (\frac{y}{\varepsilon }, \frac{x}{\varepsilon }\bigg ) \bigg \}\bigg ). \end{aligned}$$

Hence the viscosity inequalities (6.6)–(6.9) remain true.

Now for $(\frac{y}{\varepsilon },\frac{x}{\varepsilon })$ on the curve $\Gamma ^{\alpha },$ we get the following viscosity inequalities, using Proposition 2.4.

If $x\ne 0,$ then

$$\begin{aligned}&\frac{t-s}{\nu }-\frac{\Delta t}{2\nu } +\max \bigg \{ H_{\alpha }^{-} \left( \frac{\varepsilon }{\Delta x} \left\{ L_{\alpha } \left( \frac{x+\Delta x-y}{\varepsilon } \right) -L_{\alpha }\left( \frac{x-y}{\varepsilon }\right) \right\} \right) ,\\&\quad H_{\alpha }^{+} \bigg ( \frac{\varepsilon }{\Delta x} \bigg \{L_{\alpha }^{\prime }(\xi _{\alpha }^{+})\frac{x}{\varepsilon } -L_{\alpha }^{\prime }(\xi _{\alpha }^{+})\bigg (\frac{x-\Delta x}{\varepsilon }\bigg ) \bigg \}\bigg )\bigg \} \le 0. \end{aligned}$$

If $x =0$, then

$$\begin{aligned} \frac{t-s}{\nu }-\frac{\Delta t}{2\nu }+\max \bigg (A, \max _{\begin{array}{c} \alpha \end{array}} \left\{ H_{\alpha }^{-}\left( \frac{\varepsilon }{\Delta x}\bigg \{L_{\alpha } \left( \frac{\Delta x-y}{\varepsilon }\right) -L_{\alpha } \left( -\frac{y}{\varepsilon }\right) \bigg \}\right) \right\} \bigg )\le 0. \end{aligned}$$

If $y \ne 0$, then

$$\begin{aligned}&-\frac{\eta }{(T-s)^2}+\frac{t-s}{\nu } \\&\quad +\max \bigg \{ H_{\alpha }^{-} \left( L_{\alpha }^{\prime }\bigg (\frac{x-y}{\varepsilon }\bigg ) -\delta d(y,0)\right) , H_{\alpha }^{+} \bigg ( L_{\alpha }^{\prime } (\xi _{\alpha }^{-})-\delta d(y,0)\bigg )\bigg \}\ge 0. \end{aligned}$$

If $y =0$, then

$$\begin{aligned} -\frac{\eta }{(T-s)^2}+\frac{t-s}{\nu }+ \max \bigg (A,\max _{\begin{array}{c} \alpha \end{array}} H_{\alpha }^{-}\bigg (L_{\alpha }^{\prime }\bigg (\frac{x}{\varepsilon }\bigg ) \bigg )\bigg ) \ge 0. \end{aligned}$$

We now simplify the above inequalities,

$$\begin{aligned}&\text { if } x \ne 0,\qquad \frac{t-s}{\nu }-\frac{\Delta t}{2\nu }\nonumber \\&\quad +\max \bigg \{H_{\alpha }^{-}\left( L_{\alpha }^{\prime } \left( \frac{x-y}{\varepsilon }\right) \right) , H_{\alpha }^{+} (L_{\alpha }^{\prime }(\xi _{\alpha }^{+}))\bigg \} +O\left( \frac{\Delta x}{\varepsilon }\right) \le 0 \end{aligned}$$

(6.10)

$$\begin{aligned}&\text { if } x = 0, \qquad \frac{t-s}{\nu }-\frac{\Delta t}{2\nu }\nonumber \\&\quad +\max \bigg (A,\max _{\begin{array}{c} \alpha \end{array}}{H_{\alpha }}^{-} \bigg (L_{\alpha }^{\prime }\bigg (-\frac{y}{\varepsilon }\bigg )\bigg ) \bigg ) +O\bigg (\frac{\Delta x}{\varepsilon }\bigg )\le 0 \end{aligned}$$

(6.11)

$$\begin{aligned}&\text { if } y \ne 0,\qquad \frac{t-s}{\nu }\nonumber \\&\quad +\max \bigg \{H_{\alpha }^{-} \left( L_{\alpha }^{\prime }\left( \frac{x-y}{\varepsilon }\right) \right) , H_{\alpha }^{+}(L_{\alpha }^{\prime }(\xi _{\alpha }^{-}))\bigg \} +O(\sqrt{\delta })\ge \frac{\eta }{2 T^2} \end{aligned}$$

(6.12)

$$\begin{aligned}&\text { if } y = 0, \qquad \frac{t-s}{\nu }\nonumber \\&\quad +\max \bigg (A,\max _{\begin{array}{c} \alpha \end{array}} H_{\alpha }^{-} \bigg (L_{\alpha }^{\prime }\bigg (\frac{x}{\varepsilon }\bigg )\bigg )\bigg ) \ge \frac{\eta }{2 T^2}. \end{aligned}$$

(6.13)

Combining these viscosity inequalities and using Theorem 5.8 with the Hamiltonians $\chi \circ H_{\alpha }$, we deduce the same equalities for the Hamiltonians $H_{\alpha }$ as $\chi$ is a bijection. We use also the fact that $H_{\alpha }^{+}(L_{\alpha }^{\prime }(\xi _{\alpha }^{+}))=A$ and $H_{\alpha }^{+}(L_{\alpha }^{\prime }(\xi _{\alpha }^{-}))=A_{0}$, we get in all cases

$$\begin{aligned} \eta \le \mathcal {O}\left( \frac{\Delta t}{\nu }\right) +O \left( \frac{\Delta x}{\varepsilon }\right) + O(\sqrt{\delta }) =: \eta ^{\star }. \end{aligned}$$

Case$A=A_0$ In this case the function $\mathcal {D}_{{ junction}}$ is not of class $C^{1,1}$, see Proposition 5.9. So we consider the function $\mathcal {D}_{0}$ associated with $A=A_{0}+\rho$ where $\rho$ is a small parameter. The main difference with the case $A>A_{0}$ is in the case $x\in J_{\alpha }$ and $y\in J_{\beta }$ with $\alpha \ne \beta$. We only treat the case $x\in J_\alpha ^{\star }$ and $y\in J_\beta$ with $\alpha \ne \beta$ since in the other cases the arguments are the same as in the proof of the case $A>A_{0}$. Since $\mathcal {D}_{0}(\frac{y}{\varepsilon },.)$ is nondecreasing and $H_{\alpha }^{-}(p)=A_{0}$ for $p\ge 0$, and $H_{\alpha }^{+}(p)=H_{\alpha }(p)$ for $p\ge 0$, we have

$$\begin{aligned} \frac{t-s}{\nu }-\frac{\Delta t}{2\nu } +H_{\alpha }\left( \frac{\varepsilon }{\Delta x} \left\{ \mathcal {D}_0\bigg (\frac{y}{\varepsilon },\frac{x}{\varepsilon }\bigg ) -\mathcal {D}_0\bigg (\frac{y}{\varepsilon }, \frac{x-\Delta x}{\varepsilon }\bigg ) \right\} \right) \le 0. \end{aligned}$$

(6.14)

By using the Taylor expansion of the function $\mathcal {D}_{0}(\frac{y}{\varepsilon },.)$ of class $C^{1}$, there exists $\theta _{1}\in [0,1]$ such that

$$\begin{aligned}&H_{\alpha }\left( \frac{\varepsilon }{\Delta x} \left\{ \mathcal {D}_{0}\left( \frac{y}{\varepsilon },\frac{x}{\varepsilon }\right) -\mathcal {D}_{0}\left( \frac{y}{\varepsilon }, \frac{x-\Delta x}{\varepsilon }\right) \right\} \right) \\&\quad =H_{\alpha }\left( \partial _{x}\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x}{\varepsilon }\right) -\frac{\Delta x}{2\varepsilon }\partial _{xx}\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x-\theta _{1}\Delta x}{\varepsilon }\right) \right) . \end{aligned}$$

Using now a Taylor expansion of the function $H_{\alpha }$ of class $C^{2}$, there exists $\theta _{2}\in [0,1]$ such that

$$\begin{aligned}&H_{\alpha }\left( \frac{\varepsilon }{\Delta x} \left\{ \mathcal {D}_{0}\left( \frac{y}{\varepsilon }, \frac{x}{\varepsilon }\right) -\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x-\Delta x}{\varepsilon }\right) \right\} \right) \nonumber \\&\quad =H_{\alpha }\left( \partial _{x}\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x}{\varepsilon }\right) \right) -\frac{\Delta x}{2\varepsilon }\partial _{xx}\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x-\theta _{1}\Delta x}{\varepsilon }\right) H'_{\alpha }\left( \partial _{x}\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x}{\varepsilon }\right) \right) \nonumber \\&\qquad +\frac{1}{8}\left( \frac{\Delta x}{\varepsilon }\right) ^{2} \partial _{xx}\mathcal {D}_{0}\left( \frac{y}{\varepsilon }, \frac{x-\theta _{1}\Delta x}{\varepsilon }\right) ^{2}H''_{\alpha } \left( \partial _{x}\mathcal {D}_{0}\left( \frac{y}{\varepsilon }, \frac{x}{\varepsilon }\right) \right. \nonumber \\&\qquad \left. -\frac{\theta _{2}\Delta x}{2\varepsilon } \partial _{xx}\mathcal {D}_{0}\left( \frac{y}{\varepsilon }, \frac{x-\theta _{1}\Delta x}{\varepsilon }\right) \right) . \end{aligned}$$

(6.15)

Using Taylor expansion for $\partial _{x}\mathcal {D}_{0}(.,\frac{y}{\varepsilon })$ and $H'_{\alpha }$ of class $C^{1}$ there exists $\theta _{3},\theta _{4}\in [0,1]$ such that

$$\begin{aligned} H'_{\alpha }\left( \partial _{x}\mathcal {D}_{0}\left( \frac{y}{\varepsilon }, \frac{x}{\varepsilon }\right) \right)= & {} H'_{\alpha }\left( \partial _{x} \mathcal {D}_{0}\left( \frac{y}{\varepsilon },\frac{x-\theta _{1}\Delta x}{\varepsilon }\right) +\theta _{1}\frac{\Delta x}{\varepsilon }\partial _{xx} \mathcal {D}_{0}\left( \frac{y}{\varepsilon },\frac{x-\theta _{3}\Delta x}{\varepsilon }\right) \right) \nonumber \\= & {} H'_{\alpha }\left( \partial _{x}\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x-\theta _{1}\Delta x}{\varepsilon }\right) \right) \nonumber \\&+\,\theta _{1}\frac{\Delta x}{\varepsilon }\partial _{xx}\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x-\theta _{3}\Delta x}{\varepsilon }\right) H''_{\alpha }\left( \partial _{x}\mathcal {D}_{0}\left( \frac{y}{\varepsilon }, \frac{x-\theta _{1}\Delta x}{\varepsilon }\right) \right. \nonumber \\&\left. +\,\theta _{4} \frac{\Delta x}{\varepsilon }\partial _{xx} \mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x-\theta _{3}\Delta x}{\varepsilon }\right) \right) . \end{aligned}$$

(6.16)

Notice that the terms in $H_{\alpha }^{\prime \prime }$ are bounded since $\frac{x}{\varepsilon }$, $\frac{y}{\varepsilon }$ and $\frac{\Delta x}{\varepsilon \rho }$ are bounded independentely of $\Delta x\le 1$ as we take $\varepsilon =\rho =\Delta x^{\frac{2}{5}}$.

So combining (6.15) and (6.16), thanks to the $C^{1,1}$ regularity of the function $\mathcal {D}_{0}$, see Proposition 5.9 we deduce that

$$\begin{aligned}&H_{\alpha }\left( \frac{\varepsilon }{\Delta x} \left\{ \mathcal {D}_{0}\left( \frac{y}{\varepsilon }, \frac{x}{\varepsilon }\right) -\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x-\Delta x}{\varepsilon }\right) \right\} \right) \\&\quad = H_{\alpha } \left( \partial _{x}\mathcal {D}_{0} \left( \frac{y}{\varepsilon },\frac{x}{\varepsilon }\right) \right) + \mathcal {O}\left( \frac{\Delta x}{\varepsilon \sqrt{\rho }}\right) +\mathcal {O}\left( \left( \frac{\Delta x}{\varepsilon \rho }\right) ^{2}\right) . \end{aligned}$$

So combining the viscosity inequality and using the fact that $|F_A - F_{A_0}| \le \rho$ we have

$$\begin{aligned} \eta \le \mathcal {O}\left( \frac{\Delta t}{\nu }\right) +\mathcal {O}\left( \frac{\Delta x}{\varepsilon \sqrt{\rho }}\right) +\mathcal {O}\left( \left( \frac{\Delta x}{\varepsilon \rho }\right) ^{2}\right) + \mathcal {O}(\sqrt{\delta }) +\rho =: \eta ^{\star }. \end{aligned}$$

(6.17)

Step 3: Estimate of the supremum We proved in the previous step that, if $\eta > \eta ^{\star }$, then either $M_{\varepsilon ,\delta }\le 0$ or $M_{\varepsilon ,\delta }$ is reached either for $t=0$ or $s=0$.

If $t=0$, then using Theorem 2.3, we have

$$\begin{aligned} M_{\varepsilon ,\delta }\le u_0(x)-u_0(y) -\frac{\gamma }{2\varepsilon }d^{2}(y,x)+C_{T}s-\frac{s^2}{2\nu }. \end{aligned}$$

Using the fact that $u_0$ is $L_0$-Lipschitz, one can deduce

$$\begin{aligned} M_{\varepsilon ,\delta }\le & {} \sup \limits _{r\ge 0} \left( L_0 r-\frac{\gamma }{2\varepsilon }r^{2}\right) + \sup _{r>0} \left( Cr - \frac{r^2}{2\nu }\right) \\\le & {} O(\varepsilon )+O(\nu ). \end{aligned}$$

If $s=0$, then we can argue similarly (by using the stability of the numerical scheme Lemma 4.4 and get

$$\begin{aligned} M_{\varepsilon ,\delta } \le O(\varepsilon ) +O(\nu ). \end{aligned}$$

Step 4: Conclusion We proved that for $\eta > \eta ^{\star }$, $M_{\varepsilon ,\delta } \le O(\varepsilon ) + O(\nu )$. This implies that for all $(t,x) \in \mathcal {G}_h$, $t \le T/2$, we have

$$\begin{aligned} u^h(t,x)-u(t,x)\le \varepsilon \tilde{\mathcal {D}_0} \left( \frac{x}{\varepsilon },\frac{x}{\varepsilon }\right) +\frac{\delta }{2}d^2(x,0)+\frac{2\eta }{T}+ O(\varepsilon ) +O(\nu ) \end{aligned}$$

Replacing $\eta$ by $2\eta ^{\star }$ and recalling that $\tilde{\mathcal {D}}_0(x,x)\le C+A$ for all $x\in J$, we deduce that for $(t,x) \in \mathcal {G}_\varepsilon$ and $t\le T/2$ (after letting $\delta \rightarrow 0$),

$$\begin{aligned} u^h(t,x)-u(t,x)\le O \left( \frac{\Delta t}{\nu }\right) + O\left( \frac{\Delta x}{\varepsilon }\right) +O(\varepsilon )+O(\nu ). \end{aligned}$$

Using the CFL condition (1.20) and optimizing with respect to $\varepsilon$ and $\nu$ yields the desired result on $[0,\frac{T}{2})$. Doing the whole proof with u the solution of (1.6) and $u^{h}$ the solution of the corresponding scheme (1.16) with $F=F_{A}$ on [0, 2T) yields the desired result on [0, T). $\square$

Fig. 3

Error estimates for $A=A_{0}=0$ and $A=0.1>A_{0}$

Remark 8

If for all $\alpha \in \{1, \ldots , N \}$, $\min H_{\alpha }=A_{0}$, then in the case where $A=A_0$, thanks to the $C^{1,1}$ regularity of the function $D_{0}$, see Proposition 5.9, we can conclude as the case $A>A_{0}$ that the error estimate is of order $\Delta x^{\frac{1}{2}}$.

6.2 Numerical simulations

In this subsection, we give a numerical example which illustrates the convergence rate we obtained in the previous subsection.

Table 1 Error estimates for $A=A_{0}=0$

Table 2 Error estimates for $A=0.1>A_{0}$

Fig. 4

Some numerical solutions at different steps

Here we consider a junction with two branches $J_{1}=J_{2}=[0,X]$. We have the two following Hamiltonians,

$$\begin{aligned} H_{1}(p)= & {} p^{2},\\ H_{2}(p)= & {} p^{2}-1, \end{aligned}$$

and the initial data

$$\begin{aligned} u_{0}(x)=\left\{ \begin{array}{ll} 0.2x &{} \text{ if } x\in J_{1},\\ x &{} \text{ if } x\in J_{2}. \end{array}\right. \end{aligned}$$

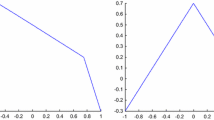
In the simulation we take $X=0.1$ and we give the error $||u(T,.)-u^{h}(T,.)||_{\infty }$ at time $T=0.01$. We compute the error in both case $A_{0}=0$ and $A=0.1>A_{0}$ with $\Delta t=\frac{\Delta x}{10}$ we get the following result, see Fig. 3 ploted in logarithmic scale and the error values in Tables 1 and 2. We give also in Figs. 4 and 5 a plot of the numerical solution for different space steps.

Fig. 5

Zoom of some numerical solutions at different steps

Remark 9

Since we don’t have any boundary condition, we initialize the scheme with a larger space domain $J'_{1}=J'_{2}= \left[ 0, X' \right]$ with $X'=0.2$ so that we allow us to loose a space step at each iteration in time, i.e. for the iteration k, we compute the solution on $\left[ 0, X_{k} \right]$ with $X_{k}=0.2-k \Delta x$. The number of time iteration is well chosen so that we get the numerical solution at time T in the space domain $X=0.1$. To compute the exact solution, we compute we approximate one with much smaller time and space step than the “real” approximate ones. For the exact solution we take $\Delta x= 10^{-6}$ and $\Delta t = 10^{-7}$.

Comments Table 2 and Fig. 3 allow us to deduce that in the case $A>A_{0}$, we get an error estimate of order $\Delta x^{\frac{1}{2}}$. Since we prove in Theorem 1.2 that the error should be at least of order $\Delta x^{\frac{1}{2}}$, we can conclude that this estimate is optimal. While in the case $A=A_{0}$, from Table 1 and Fig. 3 we get also an error estimate of order $\Delta x^{\frac{1}{2}}$ when in the proof we have $\Delta x^{\frac{2}{5}}$. So we wonder if the error estimate obtained in the proof is optimal for the case $A=A_{0}$.

A Proofs of some technical results

1.1 A.1 Proof of a priori control

In order to prove Lemma 6.1, we need the following one.

Lemma A.1

(A priori control at the same time) Assume that $u_0$ is Lipschitz continuous. Let $T>0$ and let $u^h$ be a discrete sub-solution of (1.16)–(1.18) and u be a super-solution of (1.1)–(1.2). Then there exists a constant $C=C_{T}>0$ such that for all $(t,x) \in \mathcal {G}_h$, $t \le T$, $y\in J$, we have

$$\begin{aligned} u^h(t,x)\le u(t,y)+C_{T}(1+d(x,y)). \end{aligned}$$

(A.1)

We first derive Lemma 6.1 from Lemma A.1.

Proof of Lemma 6.1

Let us fix some h and let us consider the discrete sub-solution $u^{-}$ of (1.16) and the super-solution $u^{+}$ of of (1.1) defined as :

$$\begin{aligned} u^{+}(t,x)= & {} u_0(x)+C_{0}t\\ u^{-}(n\Delta t,i\Delta x)= & {} u_0(i\Delta x)-C_{0}n\Delta t \end{aligned}$$

where

$$\begin{aligned} C_{0}=\max \bigg \{|A|,\max _{\begin{array}{c} \alpha =1,\dots ,N \end{array}} \max _{\begin{array}{c} |p_{\alpha }|\le L_{0} \end{array}}|H_{\alpha }(p_{\alpha })|;\max _{\begin{array}{c} |p_{\alpha }|\le L_{0} \end{array}}F(p_1,\dots ,p_N)\bigg \} \end{aligned}$$

and $L_0$ denotes the Lispchitz constant of $u_0$. We have for all $(t,x)\in \mathcal {G}_{h}$, with $t\le T$, $(s,y)\in [0,T)\times J$

$$\begin{aligned} u^{-}(t,x)-u^{+}(s,y)\le 2C_{0}T+L_{0}d(x,y). \end{aligned}$$

We first apply Lemma A.1 to control $u^h(t,x)-u^{-}(t,x)$ and then apply Lemma 6.1 to control $u^{+}(s,y)-u(s,y).$ Finally we get the control on $u^{h}(t,x)-u(s,y)$. $\square$

We can now prove Lemma A.1.

Proof of Lemma A.1

We define $\varphi$ in $J^2$ as

$$\begin{aligned} \varphi (x,y)=\sqrt{1+d^2(x,y)}. \end{aligned}$$

Since,

$$\begin{aligned} d^2(x,y)=\left\{ \begin{array}{l} (x-y)^2 \qquad \text {if}\quad (x,y)\in J_{\alpha }\times J_{\alpha }\\ (x+y)^2 \qquad \text {if}\quad (x,y)\in J_{\alpha }\times J_{\beta } \text{ with } \alpha \ne \beta \end{array}\right. \end{aligned}$$

we see that $d^2$ (and consequently $\varphi$) is in $C^{1,1}$ in $J^2$. Moreover $\varphi$ satisfies

$$\begin{aligned} |\varphi _{x}(x,y)|,|\varphi _{y}(x,y)|\le 1. \end{aligned}$$

(A.2)

Recalling that there exists $C>0$ such that

$$\begin{aligned} |u^h(t,x) -u_0(x) | \le C t \quad \text { and } \quad |u(t,y) - u_0(y)| \le Ct \end{aligned}$$

(see Theorem 2.3 and (4.2)) and using that $u_0$ is $L_0$-Lipschitz continuous we deduce that for all $(t,x) \in \mathcal {G}_h$, $t \le T$, $y\in J$,

$$\begin{aligned} u^h(t,x)-u(t,y)\le 2Ct+L_{0}\varphi (x,y), \end{aligned}$$

which yields the desired result. $\square$

1.2 A.2 Construction of $\tilde{F}$

Lemma A.2

There exists $\tilde{F}$, such that

• 1. $\tilde{F}$ satisfies (1.8);

• 2. $F=\tilde{F}$ in $Q_{0}$;

• 3. For $\mathbf {p} \in \mathbb {R}^N$, $(-\nabla \cdot \tilde{F})(\mathbf {p}) \le \sup _{Q_0} (-\nabla \cdot F)$.

Proof

Let $I_{\alpha }$ denote $[\underline{p}_{\alpha }^{0}; \overline{p}_\alpha ]$ so that $Q_{0}=\prod _{\alpha } I_{\alpha }.$ We then define

$$\begin{aligned} \tilde{F}(\mathbf {p})=F(\mathcal {P}_{1}(p_{1}),\dots ,\mathcal {P}_{N}(p_N)) -\sum _{\alpha =1}^N C_{\alpha }(p_{\alpha }-\mathcal {P}_{\alpha }(p_\alpha )), \end{aligned}$$

where

$$\begin{aligned} C_{\alpha }= \min _{\begin{array}{c} p\in Q_{0} \end{array}} \left( -\frac{\partial F}{\partial p_{\alpha }} (p_{1},\dots ,p_{N})\right) , \end{aligned}$$

and

$$\begin{aligned} \mathcal {P}_{\alpha }(r)={\left\{ \begin{array}{ll} \underline{p}_{\alpha }^{0} &{} \text { if } r<\underline{p}_{\alpha }^{0},\\ r &{} \text { if } r \in I_\alpha , \\ \overline{p}_\alpha &{} \text { if } r>\overline{p}_\alpha . \end{array}\right. } \end{aligned}$$

Remark that in view of the assumptions made on F, we have $C_\alpha >0$ which will ensure that (1.8) holds true. It is now easy to check that (1.8) and Item 3 are satisfied. This ends the proof of the Lemma. $\square$