Abstract
We formulate the blended force-based quasicontinuum method for multilattices and develop rigorous error estimates in terms of the approximation parameters: choice of atomistic region, blending region, and continuum finite element mesh. Balancing the approximation parameters yields a convergent atomistic/continuum multiscale method for multilattices with point defects, including a rigorous convergence rate in terms of the computational cost. The analysis is illustrated with numerical results for a Stone–Wales defect in graphene.




Similar content being viewed by others
References
Abdulle, A., Lin, P., Shapeev, A.: Numerical methods for multilattices. Multiscale Model. Simul. 10(3), 696–726 (2012)
Abdulle, A., Lin, P., Shapeev, A.: A priori and a posteriori \({W}^{1,\infty }\) error analysis of a qc method for complex lattices. SIAM J. Numer. Anal. 51(4), 2357–2379 (2013)
Abraham, F., Broughton, J., Bernstein, N., Kaxiras, E.: Spanning the continuum to quantum length scales in a dynamic simulation of brittle fracture. Europhys. Lett. 44(6), 783 (1998)
Arroyo, M., Belytschko, T.: Finite crystal elasticity of carbon nanotubes based on the exponential Cauchy-Born rule. Phys. Rev. B 69, 115415 (2004)
Badia, S., Bochev, P., Gunzburger, M., Lehoucq, R., Parks, M.: Blending methods for coupling atomistic and continuum models. In: Fish, J. (ed.) Bridging the Scales in Science and Engineering, pp. 165–186. Oxford University Press, Oxford (2009)
Badia, S., Bochev, P., Lehoucq, R., Parks, M., Fish, J., Nuggehally, M., Gunzburger, M.: A force-based blending model for atomistic-to-continuum coupling. Int. J. Multiscale Comput. Eng. 5(5), 387–406 (2007)
Badia, S., Parks, M., Bochev, P., Gunzburger, M., Lehoucq, R.: On atomistic-to-continuum coupling by blending. Multiscale Model. Simul. 7(1), 381–406 (2008)
Bauman, P., Ben Dhia, H., Elkhodja, N., Oden, J., Prudhomme, S., Prudhomme, S.: On the application of the Arlequin method to the coupling of particle and continuum models. Comput. Mech. 42, 511–530 (2008)
Born, M., Huang, K.: Dynamical Theory of Crystal Lattices, 1st edn. Clarendon Press, Oxford (1954)
Brenner, S., Scott, R.: The Mathematical Theory of Finite Element Methods, vol. 15. Springer, New York (2008)
Cauchy, A.L.: De la pression ou la tension dans un systeme de points materiels. In: Exercices de Mathematiques (1828)
Datta, D., Picu, C., Shephard, M.: Composite grid atomistic continuum method: an adaptive approach to bridge continuum with atomistic analysis. Int. J. Multiscale Comput. Eng. 2(3), 401 (2004)
Dobson, M., Elliott, R., Luskin, M., Tadmor, E.: A multilattice quasicontinuum for phase transforming materials: Cascading Cauchy Born kinematics. J. Comput. Aided Mater. Des. 14(1), 219–237 (2007)
Dobson, M., Luskin, M.: Analysis of a force-based quasicontinuum approximation. Esaim Math. Model. Numer. Anal. 42, 113–139, 0 (2008)
Dobson, M., Luskin, M., Ortner, C.: Sharp stability estimates for the force-based quasicontinuum approximation of homogeneous tensile deformation. Multiscale Model. Simul. 8(3), 782–802 (2010)
Lu, W .E.J., Yang, J.Z.: Uniform accuracy of the quasicontinuum method. Phys. Rev. B 74, 214115 (2006)
Ehrlacher, V., Ortner, C., Shapeev, A.V.: Analysis of boundary conditions for crystal defect atomistic simulations. Arch. Ration. Mech. Anal. 222(3), 1217–1268 (2016)
Eidel, B., Stukowski, A.: A variational formulation of the quasicontinuum method based on energy sampling in clusters. J. Mech. Phys. Solids 57(1), 87–108 (2009)
Ericksen, J.: On the Cauchy-Born rule. Math. Mech. Solids 13(3–4), 199–220 (2008)
Hubbard, J., Hubbard, B.: Vector calculus, linear algebra, and differential forms: a unified approach. Matrix Editions, fourth edition (2009)
Hudson, T., Ortner, C.: Analysis of stable screw dislocation configurations in an anti-plane lattice model. SIAM J. Math. Anal. 41, 291–320 (2015)
Van Koten, B., Ortner, C.: Symmetries of 2-lattices and second order accuracy of the Cauchy-Born model. SIAM Multiscale Model. Simul. 11, 615–634 (2013)
Li, X., Luskin, M., Ortner, C.: Positive definiteness of the blended force-based quasicontinuum method. Multiscale Model. Simul. 10(3), 1023–1045 (2012)
Li, X., Luskin, M., Ortner, C., Shapeev, A.V.: Theory-based benchmarking of the blended force-based quasicontinuum method. Comput. Methods Appl. Mech. Eng. 268, 763–781 (2014)
Li, X., Ortner, C., Shapeev, A.V., Van Koten, B.: Analysis of blended atomistic/continuum hybrid methods. Numer. Math. 134(2), 275–326 (2016)
Lu, J., Ming, P.: Convergence of a force-based hybrid method in three dimensions. Commun. Pure Appl. Math. 66(1), 83–108 (2013)
Lu, J., Ming, P.: Stability of a force-based hybrid method with planar sharp interface. SIAM J. Numer. Anal. 52, 2005–2026 (2014)
Luskin, M., Ortner, C.: Atomistic-to-continuum coupling. Acta Numerica 22, 397–508, 4 (2013)
Luskin, M., Ortner, C., Van Koten, B.: Formulation and optimization of the energy-based blended quasicontinuum method. Comput. Methods Appl. Mech. Eng. 253, 160–168 (2013)
Makridakis, C., Mitsoudis, D., Rosakis, P.: On atomistic-to-continuum couplings without ghost forces in three dimensions. Appl. Math. Res. Express 2014(1), 87–113 (2014)
Miller, R., Tadmor, E.: A unified framework and performance benchmark of fourteen multiscale atomistic/continuum coupling methods. Model. Simul. Mater. Sci. Eng. 17(5), 053001 (2009)
Olson, D.: Formulation and Analysis of an Optimization-Based Atomistic-to-Continuum Coupling Algorithm. PhD thesis, University of Minnesota (2015)
Olson, D., Bochev, P., Luskin, M., Shapeev, A.: Development of an optimization-based atomistic-to-continuum coupling method. In: Lirkov, I., Margenov, S., Waniewski, J. (eds.) Large-Scale Scientific Computing, volume 8353 of Lecture Notes in Computer Science, pp. 33–44. Springer, Berlin (2014)
Olson, D., Li, X., Ortner, C., Van Koten, B.: Force-Based Atomistic/Continuum Blending for multilattices. ArXiv e-prints (2016) 909
Olson, D., Ortner, C.: Regularity and locality of point defects in multilattices. Appl. Math. Res. Express 2017, 297–337 (2017)
Olson, D., Shapeev, A., Bochev, P., Luskin, M.: Analysis of an optimization-based atomistic-to-continuum coupling method for point defects. ESAIM: M2AN 50(1), 1–41 (2016)
Ortiz, M., Phillips, R., Tadmor, E.: Quasicontinuum analysis of defects in solids. Philos. Mag. A 73(6), 1529–1563 (1996)
Ortner, C.: A posteriori existence in numerical computations. SIAM J. Numer. Anal. 47(4), 2550–2577 (2009)
Ortner, C., Shapeev, A.: Interpolants of Lattice Functions for the Analysis of Atomistic/Continuum Multiscale Methods. ArXiv e-prints (2012). 1204.3705
Ortner, C., Süli, E.: A note on linear elliptic systems on \(\mathbb{R}^d\). ArXiv e-prints (2012) 1202.3970
Ortner, C., Theil, F.: Justification of the Cauchy-Born approximation of elastodynamics. Arch. Ration. Mech. Anal. 207, 1025–1073 (2013)
Ortner, C., Zhang, L.: Atomistic/continuum blending with ghost force correction. ArXiv e-prints, 1407.0053, (2014)
Scott, R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comput. 54(190), 483–493 (1990)
Seleson, P., Beneddine, S., Prudhomme, S.: A force-based coupling scheme for peridynamics and classical elasticity. Comput. Mater. Sci. 66, 34–49 (2013)
Seleson, P., Gunzburger, M.: Bridging methods for atomistic-to-continuum coupling and their implementation. Commun. Comput. Phys. 7, 831–876 (2010)
Seleson, P., Ha, Y.D., Beneddine, S.: Concurrent coupling of bond-based peridynamics and the navier equation of classical elasticity by blending. Int. J. Multiscale Comput. Eng. 13, 91–113 (2015)
Shapeev, A.V.: Consistent energy-based atomistic/continuum coupling for two-body potentials in three dimensions. SIAM J. Sci. Comput. 34(3), B335–B360 (2012)
Shapeev, A.V.: Consistent energy-based atomistic/continuum coupling for two-body potentials in one and two dimensions. SIAM J. Multiscale Model. Simul. 9, 905–932 (2011)
Shenoy, V.B., Miller, R., Tadmor, E.B., Rodney, D., Phillips, R., Ortiz, M.: An adaptive finite element approach to atomic-scale mechanics-the quasicontinuum method. J. Mech. Phys. Solids 47(3), 611–642 (1999)
Shilkrot, L., Miller, R., Curtin, W.: Coupled atomistic and discrete dislocation plasticity. Phys. Rev. Lett. 89(2), 025501 (2002)
Shimokawa, T., Mortensen, J.J., Schiøtz, J., Jacobsen, K.W.: Matching conditions in the quasicontinuum method: removal of the error introduced at the interface between the coarse-grained and fully atomistic region. Phys. Rev. B 69, 214104 (2004)
Stillinger, F., Weber, T.: Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 31(8), 5262 (1985)
Tadmor, E., Miller, R.: Modeling Materials Continuum, Atomistic and Multiscale Techniques, 1st edn. Cambridge University Press, Cambridge (2011)
Xiao, S.P., Belytschko, T.: A bridging domain method for coupling continua with molecular dynamics. Comput. Methods Appl. Mech. Eng. 193(17), 1645–1669 (2004)
Yang, Jerry Z, Weinan, E.: Generalized Cauchy–Born rules for elastic deformation of sheets, plates, and rods: derivation of continuum models from atomistic models. Phys. Rev. B 74(18), 184110 (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
DO was supported by the National Science Foundation PIRE Grant OISE-0967140 and NSF RTG program DMS-1344962. XL was supported by the Simons Collaboration Grant with Award ID: 426935 and NSF DMS-1720245. CO was supported by European Research Council Starting Grant 335120.
A Notation
A Notation
This appendix summarizes notation used in the manuscript.
-
\(\mathcal {L}\)—a Bravais lattice
-
\(\mathcal {M}\)—a multilattice
-
\(\mathcal {S} = \{0, \ldots , S-1\}\)—the index set of atomic species
-
\(\xi \)—an element of \(\mathcal {L}\) or \(\epsilon \mathcal {L}\) for \(\epsilon > 0\).
-
\(\alpha ,\beta ,\gamma ,\delta , \iota , \chi \)—indexes denoting atomic species
-
\(\rho , \tau , \sigma \in \mathcal {L}\)—vectors between lattice sites
-
\(\mathcal {R}\)—an interaction range whose elements are triples of the form \((\rho \alpha \beta )\in \mathcal {L} \times \mathcal {S} \times \mathcal {S}\)
-
\(\mathcal {R}_1 := \{ \rho \in \mathcal {L} : \exists (\rho \alpha \beta )\in \mathcal {R}\}\)—projection of \(\mathcal {R}\) onto lattice direction
-
\(\mathrm{conv}\)—notation for the convex hull of a set
-
\(r_{\mathrm{cut}}:=\max \{ |\rho |: \rho \in \mathcal {R}_1\}\)—a finite cut-off distance for interaction range
-
\(\nu _x := B_{2r_{\mathrm{cut}}}(0)\)—buff region up to twice interaction range
-
\(r_{\mathrm{cell}}\)—the radius of the smallest ball inscribing the unit cell of \(\mathcal {L}\)
-
\(r_{\mathrm{buff}} := \max \{ r_{\mathrm{cut}}, r_{\mathrm{cell}}\}\)
-
\(\varvec{u} = \big (u_\alpha \big )_{\alpha = 0}^{S-1}\)—vector of displacements of all species of atoms
-
\((U, \varvec{p})\)—displacement/shift description defined by \(U = u_0\) and \(p_\alpha = u_\alpha - u_0\)
-
\(\varvec{y}^\mathrm{ref}\) and \(\varvec{p}^\mathrm{ref}\)—the reference deformation and shifts
-
\(D_{(\rho \alpha \beta )} \varvec{u}(\xi ) = u_\beta (\xi + \rho ) - u_\alpha (\xi ), D_{(\rho \alpha \beta )}(U,\varvec{p}) = U(\xi +\rho ) - U(\xi ) + p_\beta (\xi + \rho ) - p_\alpha (\xi )\)
-
\(D\varvec{u}(\xi ) = \big (D_{(\rho \alpha \beta )}\varvec{u}(\xi )\big )_{(\rho \alpha \beta )\in \mathcal {R}}, D(U,\varvec{p})(\xi ) = \big (D_{(\rho \alpha \beta )}(U,\varvec{p})(\xi )\big )_{(\rho \alpha \beta )\in \mathcal {R}}\)
-
\(\hat{V}_\xi (D\varvec{y}(\xi ))\) and \(V_\xi (D\varvec{u})\)—site potentials defined on deformations and displacements, respectively
-
\(\mathcal {E}^\mathrm{a}(\varvec{u})\) and \(\mathcal {E}^\mathrm{a}_{\mathrm{hom}}(\varvec{u})\)—energy difference functionals for defective and defect free lattice.
-
\(\mathcal {T}_{\mathrm{a}}\)—atomistic scale finite element mesh of triangles in 2D and tetrahedra in 3D
-
\(\bar{\zeta }(x), \bar{\zeta }_\xi (x) = \bar{\zeta }(x-\xi )\)—nodal basis function of \(\mathcal {T}_\mathrm{a}\) associated with the origin and \(\xi \) respectively
-
\(\omega _{\rho }(x):= \int _{0}^1 \bar{\zeta }(x+t\rho )dt\)—an auxiliary function
-
\(Iu_\alpha , IU, Ip_\alpha \) or \(\bar{u}_\alpha , \bar{U}, \bar{p}_\alpha \)—a piecewise linear interpolant with respect to \(\mathcal {T}_\mathrm{a}\)
-
\(\tilde{I}u_\alpha , \tilde{I}U, \tilde{I}p_\alpha \) or \(\tilde{u}_\alpha , \tilde{U}, \tilde{p}_\alpha \)—a \(\mathrm{C}^{2,1}\) interpolant with respect to \(\mathcal {T}_\mathrm{a}\)
-
\(u^*(x) := (\bar{\zeta } * \bar{u})(x)\)—quasi-interpolant of u defined through convolution
-
\(|\cdot |\)—meaning depends on context: \(|\cdot |\) is \(\ell ^2\) norm of a vector, matrix, higher order tensor, or finite difference stencil. |T| is area or volume of element T in a finite element partition, \(|\gamma |\) is the order of a multiindex.
-
\(\Vert \cdot \Vert _{\ell ^2(A)}\)—\(\ell ^2\) norm over a set A. If \(f:A \rightarrow \mathbb {R}^d\) is a vector-valued function, \(\Vert f\Vert _{\ell ^2(A)} = (\sum _{\alpha \in A}|f(\alpha )|^2)^{1/2}\).
-
\(\Vert \cdot \Vert _{\mathrm{a}}\)—norm on admissible displacements defined by \(\Vert \varvec{u}\Vert _\mathrm{a}^2 := \sum _{\alpha = 0}^{S-1}\Vert \nabla Iu_\alpha \Vert _{L^2(\mathbb {R}^d)}^2 + \sum _{\alpha \ne \beta }\Vert Iu_\alpha - Iu_\beta \Vert _{L^2(\mathbb {R}^d)}^2\).
-
\(\varvec{\mathcal {U}}\) —space of admissible displacements defined by
$$\begin{aligned} \mathcal {U} :=~ \left\{ \varvec{u} = (u_\alpha )_{\alpha = 0}^{S-1} : u_\alpha :\mathcal {L} \rightarrow \mathbb {R}^n, \Vert \varvec{u}\Vert _\mathrm{a}< \infty \right\} /\mathbb {R}^n \end{aligned}$$ -
\(\varvec{\mathcal {U}}_0\) —space of test displacements defined by
$$\begin{aligned} \left\{ (U, \varvec{p}) : \mathrm{supp}(\nabla IU), \, p_0 \equiv 0, \, \text{ and } \, \mathrm{supp}(Ip_\alpha ) \, \text{ are } \text{ compact }\right\} /\mathbb {R}^n \end{aligned}$$ -
\(\varOmega \)—a finite polygonal domain
-
\(\varphi \) —the blending function
-
\(\varOmega _\mathrm{a}:=~ \mathrm{supp}(1-\varphi ) + B_{2r_{\mathrm{buff}}}\)—the atomistic domain
-
\(\varOmega _{\mathrm{b}} :=~ \mathrm{supp}(\nabla \varphi ) + B_{2r_{\mathrm{buff}}}\)—the blending region
-
\(\varOmega _\mathrm{c}:=~ {\mathrm{supp}}(\varphi ) \cap \varOmega + B_{2r_{\mathrm{buff}}}\)—the continuum region
-
\(\varOmega _{\mathrm{core}} :=~ \varOmega \setminus \varOmega _\mathrm{c}\)—the defect core region
-
\(\mathcal {T}_h\)—the (coarse) finite element mesh on \(\varOmega \)
-
\(h(x) := \max _{T: x\in T} \mathrm{Diam}(T)\)—the mesh size function
-
\(R_{\mathrm{t}} := \inf _{R} \{R > 0: \varOmega _{\mathrm{t}} \subset B_{R}(0)\}\)—an exterior measure of a domain \(\varOmega _{\mathrm{t}}\)
-
\(r_{\mathrm{t}} := \sup _{r}\{r > 0: B_{r}(0) \subset \varOmega _{\mathrm{t}}\}\)—an interior measure of a domain \(\varOmega _{\mathrm{t}}\)
-
\(R_{\mathrm{o}} := \inf _{R} \{R > 0: \varOmega \subset B_{R}(0)\}\) —an exterior measurement of \(\varOmega \)
-
\(r_{\mathrm{i}} := \sup _{r}\{r > 0: B_{r}(0) \subset \varOmega \}\)—an interior measurement of \(\varOmega \)
-
\(\varOmega _{\mathrm{ext}} := \mathbb {R}^d\setminus B_{r_{\mathrm{i}}/2}(0)\)—exterior of \(\varOmega \)
-
\(I_h\)— the standard piecewise linear nodal interpolant on \(\mathcal {T}_h\)
-
\(S_{h}\)—the Scott-Zhang quasi-interpolant on \(\mathcal {T}_h\).
-
\(W_{\mathrm{CB}}(U,\varvec{p})\)—Cauchy–Born strain energy density function
-
\(\mathcal {E}^\mathrm{c}(U,\varvec{p})\)—Cauchy–Born energy functional
-
\(\mathcal {U}_h :=~ \left\{ u \in \mathrm{C}^0(\varOmega ) : u|_{T} \in \mathcal {P}_1(T), \quad \forall \, T \in \mathcal {T}_h\right\} \)—a finite element space
-
\(\varvec{\mathcal {U}}_h :=~ \mathcal {U}_h / \mathbb {R}^n\) space of admissible finite element displacements
-
\(\mathcal {U}_{h,0} :=~ \left\{ u \in \mathrm{C}^0(\mathbb {R}^d): u|_{T} \in \mathcal {P}_1(T), \quad \forall \, T \in \mathcal {T}_h, u = 0 \text{ on } \mathbb {R}^d\setminus \varOmega \right\} \)—finite element space satisfying homogeneous boundary conditions
-
\(\varvec{\mathcal {U}}_{h,0} :=~ \mathcal {U}_{h,0}/ \mathbb {R}^n\)—finite element quotient space
-
\(\varvec{\mathcal {P}}_{h,0} :=~ \{0\} \times (\mathcal {U}_{h,0})^{S-1}\)—finite element space for shifts
-
\(\Vert (U, \varvec{p})\Vert _{\mathrm{ml}}^2 := \Vert \nabla U \Vert _{L^2(\mathbb {R}^d)}^2 + \sum _{\alpha = 0}^{S-1}\Vert p_\alpha \Vert ^2_{L^2(\mathbb {R}^d)} = \Vert \nabla U \Vert _{L^2(\mathbb {R}^d)}^2 + \Vert \varvec{p}\Vert ^2_{L^2(\mathbb {R}^d)}\)—norm on finite element spaces
-
\(\Vert \varvec{p}\Vert _{L^p} := \sum _{\alpha = 0}^{S-1}\Vert p_\alpha \Vert _{L^p}, \Vert \nabla \varvec{p}\Vert _{L^p} := \sum _{\alpha = 0}^{S-1}\Vert \nabla p_\alpha \Vert _{L^p}\)
-
\(\eta (x)\)—a smooth bump function or standard mollifying function depending on the context
-
\(T_{R}u_\alpha (x) = \eta (x/R)\bigg (Iu_\alpha - \frac{1}{|A_R|}\int \limits _{A_R} Iu_0\, dx\bigg )\)—a truncation operator
-
\(\varPi _{h} u_\alpha := S_h (T_{r_{\mathrm{i}}}u_\alpha )\)—an projection operator from discrete displacements to finite element displacements
-
\(\varPi _{h} p_\alpha := \varPi _{h} (u_\alpha - u_0)\) —- a projection operator on shifts
-
\([\mathrm{{S}^\mathrm{c}_{\mathrm{d}}}(U,\varvec{q})(x)]_{\beta }\) and \([\mathrm{{S}^\mathrm{c}_{\mathrm{s}}}(U,\varvec{q})(x)]_{\alpha \beta }\)— continuum stress function associated with displacements and shifts
-
\([\,\mathrm{S}^\mathrm{a}_{\mathrm{d}}(U,\varvec{q})(x)]_\beta \) and \([\,\mathrm{S}^\mathrm{a}_{\mathrm{s}}(U,\varvec{q})(x)]_{\alpha \beta }\) —atomistic stress function associated with displacements and shifts
-
\(V_{,(\rho \alpha \beta )(\tau \gamma \delta )}\big ( \cdot \big ):v:w :=~ w^{{\top }}\big [V_{,(\rho \alpha \beta )(\tau \gamma \delta )}\big ( \cdot \big )\big ]v \quad \forall v,w \in \mathbb {R}^n\)
-
\(\mathbb {C} : D(W,\varvec{q}): D(Z,\varvec{r}) :=~ \sum _{\begin{array}{c} (\rho \alpha \beta )\\ (\tau \gamma \delta ) \end{array}} V_{,(\rho \alpha \beta )(\tau \gamma \delta )}:D_{(\rho \alpha \beta )}(W,\varvec{q}):D_{(\tau \gamma \delta )}(Z,\varvec{r})\)
-
\(\mathbb {C} : \nabla (W,\varvec{q}): \nabla (Z,\varvec{r}) :=~ \sum _{\begin{array}{c} (\rho \alpha \beta )\\ (\tau \gamma \delta ) \end{array}} V_{,(\rho \alpha \beta )(\tau \gamma \delta )}:(\nabla _\rho W + q_\beta - q_\alpha ):(\nabla _\tau Z + r_\beta - r_\alpha )\)
-
\(\varphi _n\)—a sequence of blending functions
-
\(\psi _n := 1-\varphi _n\)
-
\(\theta _n := \sqrt{\psi _n}\)
-
\(B_{r}, B_{r}(x)\)—Ball of radius r about the origin or ball of radius r about x.
-
\(\mathrm{supp}(f)\)—support of a function f.
-
\(\mathrm{Diam}(U)\)—diameter of the set U measured with the Euclidean norm.
-
\((\mathbb {R}^n)^{\mathcal {R}}\)—direct product of vectors with \(|\mathcal {R}|\) terms.
-
 —transpose of a matrix.
—transpose of a matrix. -
\(\otimes \)—tensor product.
-
\(\nabla ^j\)—jth derivative of a function defined on \(\mathbb {R}^d\).
-
\(\partial _\gamma \)—multiindex notation for derivatives.
-
\(L^p(U)\)—Standard Lebesgue spaces.
-
\(W^{k,p}(U)\)—Standard Sobolev spaces.
-
\(W^{k,p}_{\mathrm{loc}}(U) = \left\{ f:U \rightarrow \mathbb {R}^d : f \in W^{k,p}(V) \, \forall V \subset \subset U \right\} \).
-
\(H^k(U) = W^{k,2}(U)\), \(H^1_0(U) = \left\{ f \in H^k(U) : \text{ Trace }(f) = 0~\, \text{ on } \,~ \partial U \right\} \).
-
\(\mathrm{C}^{k}\)—space of k times continuously differentiable functions.
-
\(C^{k,1}\)—space of functions having continuous derivatives up to order k, and whose k-th partial derivatives are Lipschitz continuous.
-
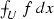 —average value of f over U.
—average value of f over U.
Rights and permissions
About this article
Cite this article
Olson, D., Li, X., Ortner, C. et al. Force-based atomistic/continuum blending for multilattices. Numer. Math. 140, 703–754 (2018). https://doi.org/10.1007/s00211-018-0979-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-018-0979-x



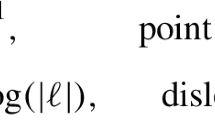
 —transpose of a matrix.
—transpose of a matrix.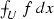 —average value of f over U.
—average value of f over U.