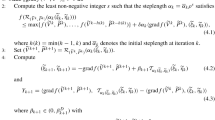Abstract
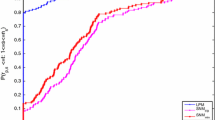
We compare various algorithms for constructing a matrix of order \(n\) whose Pareto spectrum contains a prescribed set \(\Lambda =\{\lambda _1,\ldots , \lambda _p\}\) of reals. In order to avoid overdetermination one assumes that \(p\) does not exceed \(n^2.\) The inverse Pareto eigenvalue problem under consideration is formulated as an underdetermined system of nonlinear equations. We also address the issue of computing Lorentz spectra and solving inverse Lorentz eigenvalue problems.
Similar content being viewed by others
References
Adly, S., Seeger, A.: A nonsmooth algorithm for cone-constrained eigenvalue problems. Comput. Optim. Appl. 49, 299–318 (2011)
Ben-Israel, A.: A Newton-Raphson method for the solution of systems of equations. J. Math. Anal. Appl. 15, 243–252 (1966)
Chen, X., Nashed, Z., Qi, L.: Convergence of Newton’s method for singular smooth and nonsmooth equations using adaptive outer inverses. SIAM J. Optim. 7, 445–462 (1997)
Chu, M.T., Golub, G.H.: Inverse Eigenvalue Problems: Theory, Algorithms, and Applications. Oxford University Press, New York (2005)
Clarke, F.H.: Optimization and Nonsmooth Analysis. Wiley, New York (1983)
Gowda, M.S., Sznajder, R., Tao, J.: Some \(P\)-properties for linear transformations on Euclidean Jordan algebras. Linear Algebra Appl. 393, 203–232 (2004)
Facchinei, F., Pang, J.P.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer, New York (2003)
Forsythe, G.E., Golub, G.H.: On the stationary values of a second-degree polynomial on the unit sphere. J. Soc. Indust. Appl. Math. 13, 1050–1068 (1965)
Fiedler, M.: Positivity with respect to the round cone. Mat. Casopis Sloven. Akad. Vied 24, 155–159 (1974)
Gajardo, P., Seeger, A.: Reconstructing a matrix from a partial sampling of Pareto eigenvalues. Comput. Optim. Appl. 51, 1119–1135 (2012)
Gander, W.: Least squares with a quadratic constraint. Numer. Math. 36, 291–307 (1981)
Gander, W., Golub, G.H., von Matt, U.A.: A constrained eigenvalue problem. Linear Algebra Appl. 114(115), 815–839 (1989)
He, J.-S., Li, C., Wang, J.-H.: Newton’s method for underdetermined systems of equations under the \(\gamma \)-condition. Numer. Funct. Anal. Optim. 28, 663–679 (2007)
Huang, Z.J.: A new method for solving nonlinear underdetermined systems. Comput. Appl. Math. 13, 33–48 (1994)
Humes, C., Júdice, J.J., Queiroz, M.: The symmetric eigenvalue complementarity problem. Math. Comp. 73, 1849–1863 (2004)
Júdice, J.J., Raydan, M., Rosa, S.S., Santos, S.A.: On the solution of the symmetric eigenvalue complementarity problem by the spectral projected gradient algorithm. Numer. Algor. 47, 391–407 (2008)
Júdice, J.J., Ribeiro, I.M., Sherali, H.D.: The eigenvalue complementarity problem. Comput. Optim. Appl. 37, 139–156 (2007)
Júdice, J.J., Ribeiro, I.M., Rosa, S.S., Sherali, H.D.: On the asymmetric eigenvalue complementarity problem. Optim. Methods Softw. 24, 549–586 (2009)
Loewy, R., Schneider, H.: Positive operators on the \(n\)-dimensional ice cream cone. J. Math. Anal. Appl. 49, 375–392 (1975)
Martínez, J.M.: Quasi-Newton methods for solving underdetermined nonlinear simultaneous equations. J. Comput. Appl. Math. 34, 171–190 (1991)
Pinto da Costa, A., Seeger, A.: Numerical resolution of cone-constrained eigenvalue problems. Comput. Appl. Math. 28, 37–61 (2009)
Pinto da Costa, A., Seeger, A.: Cone-constrained eigenvalue problems: theory and algorithms. Comput. Optim. Appl. 45, 25–57 (2010)
Qi, L., Sun, J.: A nonsmooth version of Newton’s method. Math. Program. 58, 353–367 (1993)
Quittner, P.: Spectral analysis of variational inequalities. Comment. Math. Univ. Carolin. 27, 605–629 (1986)
Seeger, A.: Eigenvalue analysis of equilibrium processes defined by linear complementarity conditions. Linear Algebra Appl. 292, 1–14 (1999)
Seeger, A., Torki, M.: On eigenvalues induced by a cone constraint. Linear Algebra Appl. 372, 181–206 (2003)
Seeger, A., Torki, M.: Local minima of quadratic forms on convex cones. J. Global Optim. 44, 1–28 (2009)
Tanabe, K.: Continuous Newton-Raphson method for solving an underdetermined system of nonlinear equations. Nonlinear Anal. 3, 495–503 (1979)
Walker, H.F.: Newton-like methods for underdetermined systems. In: Computational Solution of Nonlinear Systems of Equations (Fort Collins, 1988), pp. 679–699. Lectures in Appl. Math., vol. 26. American Mathematical Society, Providence (1990)
Walker, H.F., Watson, L.T.: Least-change secant update methods for underdetermined systems. SIAM J. Numer. Anal. 27, 1227–1262 (1990)
Acknowledgments
The first author has been supported by Projet Fondecyt Nr. 1080173 (Chile) and “Programa de Financiamiento Basal” from the Center of Mathematical Modeling, Universidad de Chile. He thanks also the University of Avignon for the hospitality and working facilities offered during a visit at this institution.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gajardo, P., Seeger, A. Solving inverse cone-constrained eigenvalue problems. Numer. Math. 123, 309–331 (2013). https://doi.org/10.1007/s00211-012-0487-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-012-0487-3