Derived equivalences of canonical covers of hyperelliptic and Enriques surfaces in positive characteristic

Abstract

We prove that any Fourier–Mukai partner of an abelian surface over an algebraically closed field of positive characteristic is isomorphic to a moduli space of Gieseker-stable sheaves. We apply this fact to show that the set of Fourier–Mukai partners of a canonical cover of a hyperelliptic or Enriques surface over an algebraically closed field of characteristic greater than three is trivial. These results extend earlier results of Bridgeland–Maciocia and Sosna to positive characteristic.

1 Introduction

The main motivation of this paper is the recent series of results in the study of equivalences of derived categories of sheaves of smooth projective varieties over fields other than the field of complex numbers. For instance, over finite fields, the first named author proves that the Hasse–Weil zeta function of an abelian variety, as well as of smooth varieties of dimension at most three, is unaltered under equivalences of derived categories [9, 11]. Moreover, Ward in his thesis [35] produces examples of genus one curves over ${\mathbf {Q}}$ admitting an arbitrary number of distinct Fourier–Mukai partners, revealing in this way consistent differences with the case of elliptic curves over ${\mathbf {C}}$. Finally, Lieblich and Olsson in [17] extend to positive characteristic seminal works of Mukai and Orlov concerning derived equivalences of K3 surfaces. In particular, they prove that any Fourier–Mukai partner of a K3 surface X over an algebraically closed field of characteristic $p\ne 2$ is a moduli space of Gieseker-stable sheaves on X, and in addition X admits only a finite number of Fourier–Mukai partners. While Orlov’s proof relies on Hodge theory, Lieblich–Olsson’s proof relies on deformation theory of perfect complexes and on the theory of liftings to the Witt ring.

Inspired by the results of [17], in this paper we focus on special classes of abelian and K3 surfaces that arise as canonical covers of hyperelliptic and Enriques surfaces. Our first main result is an extension of a work of Sosna [34, Theorem 1.1] to positive characteristic.

Theorem 1.1

Let S be a hyperelliptic surface over an algebraically closed field of characteristic $p>3$ and let A be its canonical cover. Then any smooth projective surface that is derived equivalent to A is isomorphic to either A or its dual ${\widehat{A}}$.

We refer to Theorem 4.4 for a slightly stronger result. One of the main ingredients in the proof of Theorem 1.1 is the characterization of Fourier–Mukai partners of abelian surfaces in positive characteristic as moduli spaces of Gieseker-stable sheaves. In particular we extend the result [6, Theorem 5.1] of Bridgeland–Maciocia to positive characteristic. In the following we denote by ${\mathbf {D}}(X)$ the bounded derived category of coherent sheaves on a smooth projective variety X.

Theorem 1.2

Let A be an abelian surface over an algebraically closed field k of positive characteristic and let Y be a smooth projective variety over k. Suppose furthermore that there is an equivalence of triangulated categories $\Phi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(Y)$. Then Y is an abelian surface and A is isomorphic to a moduli space of Gieseker-stable sheaves on either Y or its dual ${\widehat{Y}}$.

The proof of the previous theorem is based on the notion of filtered equivalence (cf. [17, 18]). We recall that a derived equivalence $\Phi :{\mathbf {D}}(X)\rightarrow {\mathbf {D}}(Y)$ of surfaces induces a homomorphism $\Phi ^{\mathrm{CH}}:{\mathrm{CH}}^*(X)\rightarrow \mathrm{CH}^*(Y)$ between the numerical Chow groups. Then one says that $\Phi$ is filtered if $\Phi ^{\mathrm{CH}}(0,0,1)=(0,0,1)$. In Proposition 3.1 we show that in the case of abelian surfaces, a filtered equivalence induces an isomorphism between the surfaces. Hence in order to complete the proof of Theorem 1.2, we construct an equivalence of derived categories

$$\begin{aligned} \Xi :{\mathbf {D}}(A){\mathop {\longrightarrow }\limits ^{\Phi }}{\mathbf {D}}(Y){\mathop {\longrightarrow }\limits ^{\Psi }} {\mathbf {D}}(Y) \end{aligned}$$

where $\Psi$ is an autoequivalence such that the moduli space ${{\mathcal {M}}}_Y(v)$ of Gieseker-stable sheaves with $v=\Xi ^{\mathrm{CH}}(0,0,1)$ is a smooth surface that admits a universal family ${{\mathcal {U}}}$. This completes the proof as the composition of $\Xi$ with the Fourier–Mukai functor associated to ${{\mathcal {U}}}$ is a filtered equivalence. We have been able to perform this strategy only if the rank component r of $\Phi ^{\mathrm{CH}}(0,0,1)$ is non-zero. In the other case $r=0$, we had to involve Mukai’s equivalence ${{\mathcal {S}}}_Y:{\mathbf {D}}(Y)\rightarrow {\mathbf {D}}({\widehat{Y}})$ induced by the Poincaré bundle in order to apply the same plan. This explains why the conclusions of Theorem 1.2 and [6, Theorem 5.1] are not completely symmetric.

In Sect. 6 we observe that one can push the techniques of [17] a little further in order to prove that K3 surfaces that are canonical covers of Enriques surfaces in characteristic $p>3$ do not admit any non-trivial Fourier–Mukai partner. This in particular extends the second part of the result of Sosna [34, Theorem 1.1] to positive characteristic.

Theorem 1.3

Let S be an Enriques surface over an algebraically closed field of characteristic $p>3$ and let X be its canonical cover. Then any smooth projective surface that is derived equivalent to X is isomorphic to X.

1.1 Notation

Unless otherwise specified we work over an algebraically closed field k of positive characteristic p.

2 Background material

2.1 Fourier–Mukai transforms and Chow groups

Let k be an algebraically closed field of positive characteristic p. The bounded derived category of sheaves of a smooth projective variety X is defined as ${\mathbf {D}}(X):=D^b\big ({\mathcal {C}}oh(X) \big )$. The category ${\mathbf {D}}(X)$ is k-linear and triangulated. If Y is another smooth projective variety, an object ${{\mathcal {E}}}$ in ${\mathbf {D}}(X\times Y)$ defines a Fourier–Mukai functor via the assignment:

$$\begin{aligned} \Phi _{{{\mathcal {E}}}} : {\mathbf {D}}(X) \rightarrow {\mathbf {D}}(Y), \quad {{\mathcal {F}}}\mapsto {\mathbf {R}}p_{2*}\big (p_1^*{{\mathcal {F}}}{\mathop {\otimes }\limits ^{{\mathbf {L}}}} {{\mathcal {E}}}\big ) \end{aligned}$$

where $p_1$ and $p_2$ denote the projections from $X\times Y$ onto the first and second factor respectively. An important theorem of Orlov tells us that any equivalence $F:{\mathbf {D}}(X)\rightarrow {\mathbf {D}}(Y)$ is of Fourier–Mukai type, i.e. there exists a unique up to isomorphism kernel${{\mathcal {E}}}$ in ${\mathbf {D}}(X\times Y)$ such that $F\simeq \Phi _{{{\mathcal {E}}}}$. Finally we recall that the composition of Fourier–Mukai transforms is again of Fourier–Mukai type.

Now consider an abelian surface A over k. We denote by ${\mathrm{CH}}^*(A)_{\mathrm{num}}=\oplus _i \mathrm{CH}^i(A)_{\mathrm{num}}$ the graded ring of algebraic cycles modulo numerical equivalence so that

$$\begin{aligned} \mathrm{CH}^0(A)_{\mathrm{num}}\simeq {\mathbf {Z}}, \quad \mathrm{CH}^1(A)_\mathrm{num}\simeq \mathrm{NS}(A)\quad \hbox {and}\quad \mathrm{CH}^2(A)_\mathrm{num}\simeq {\mathbf {Z}}, \end{aligned}$$

where $\mathrm{NS}(A)$ denotes the Néron–Severi group of A up to torsion. Moreover we set $\mathrm{CH}^*(A)_{\mathrm{num},{\mathbf {Q}}}:=\mathrm{CH}^*(A)_{\mathrm{num}}\otimes {\mathbf {Q}}$. For an object ${{\mathcal {F}}}$ in ${\mathbf {D}}(A)$ we denote by $v({{\mathcal {F}}})\in \mathrm{CH}^*(A)_{\mathrm{num},{\mathbf {Q}}}$ its Mukai vector (see [7, Sect. 5.2] and [2, p. 3]). Hence the Mukai vector of a locally free sheaf E on A is $v(E)=\big (\mathrm{rk}(E), \, c_1(E),\, \chi (E)\big )$ and the map

$$\begin{aligned} v:{\mathbf {D}}(A)\rightarrow \mathrm{CH}^*(A)_{\mathrm{num},{\mathbf {Q}}} \end{aligned}$$

factors through the Grothendieck group K(A) of locally free sheaves via the Chern character

$$\begin{aligned} \mathrm{ch}: K(A) \; \rightarrow \mathrm{CH}^*(A)_{\mathrm{num},{\mathbf {Q}}}. \end{aligned}$$

Finally, we denote the Mukai pairing on $\mathrm{CH}^*(A)_{\mathrm{num},{\mathbf {Q}}}$ by

$$\begin{aligned} \langle (r,l,\chi ), \, (r',l',\chi ')\rangle _A := l\cdot l' \,- \, r \,\chi ' - \chi \, r', \end{aligned}$$

so that by the Grothendieck–Riemann–Roch Theorem there are equalities

$$\begin{aligned} \langle v({{\mathcal {F}}}), \, v({{\mathcal {G}}})\rangle _A = -\,\chi ({{\mathcal {F}}},{{\mathcal {G}}})\quad \hbox { for any objects } {{\mathcal {F}}},{{\mathcal {G}}}\hbox { in } {\mathbf {D}}(A) \end{aligned}$$

(2.1)

(as usual $\chi ({{\mathcal {F}}},{{\mathcal {G}}})=\sum _{i} (-1)^i \mathrm{dim}\, \mathrm{Hom}_{{\mathbf {D}}(A)}^i({{\mathcal {F}}},{{\mathcal {G}}})$).

Given another abelian surface B, a Fourier–Mukai functor $\Phi _{{{\mathcal {E}}}}:{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(B)$ induces a group homomorphism $\Phi _{{{\mathcal {E}}}}^{\mathrm{CH}}:\mathrm{CH}^*(A)_{\mathrm{num},{\mathbf {Q}}} \rightarrow \mathrm{CH}^*(B)_{\mathrm{num},{\mathbf {Q}}}$ through the formula

$$\begin{aligned} \Phi _{{{\mathcal {E}}}}^{\mathrm{CH}}(-) := \mathrm{pr}_{2*}\big (\mathrm{pr}_1^*(-) \, \cdot \, v({{\mathcal {E}}})\big ) \end{aligned}$$

where $\mathrm{pr}_1$ and $\mathrm{pr}_2$ denote the projections from the product $A\times B$ onto the first and second factor respectively. We point out that in general $\Phi _{{{\mathcal {E}}}}^{\mathrm{CH}}$ does not respect the grading. As showed in [7] and [10, Sect. 3], we have that $\big (\Phi _{{{\mathcal {E}}}}\circ \Phi _{{{\mathcal {E}}}'}\big )^{\mathrm{CH}} \simeq \Phi _{{{\mathcal {E}}}}^{\mathrm{CH}} \circ \Phi _{{{\mathcal {E}}}'}^{\mathrm{CH}}$, and that $\Phi _{{{\mathcal {E}}}}^{\mathrm{CH}}$ is invertible if $\Phi _{{{\mathcal {E}}}}$ is an equivalence. Finally, we note that if $\Phi _{{{\mathcal {E}}}}$ is an equivalence, then it follows that

$$\begin{aligned} \big \langle \Phi _{{{\mathcal {E}}}}^{\mathrm{CH}} \big (v({{\mathcal {F}}}) \big ), \, \Phi _{{{\mathcal {E}}}}^{\mathrm{CH}}\big (v({{\mathcal {G}}}) \big ) \big \rangle _B = \big \langle v({{\mathcal {F}}}),\quad v({{\mathcal {G}}}) \big \rangle _A \end{aligned}$$

(2.2)

from (2.1), and by the fact that $v\circ \Phi _{{{\mathcal {E}}}}=\Phi _{{{\mathcal {E}}}}^{\mathrm{CH}}\circ v$.

We conclude this subsection by pointing out the following peculiar fact true for abelian surfaces. Its proof is identical to that of [7, Corollary 9.43] with the opportune modifications. Moreover it holds in any dimension.

Proposition 2.1

If $\Phi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(B)$ is an equivalence of derived categories of abelian surfaces, then

$$\begin{aligned} \Phi ^{\mathrm{CH}}\big (\mathrm{CH}^*(A)_{\mathrm{num}}\big ) = \mathrm{CH}^*(B)_{\mathrm{num}}. \end{aligned}$$

We will tacitly use the previous result throughout the rest of the paper.

Notation 2.2

Given an abelian surface A over k we denote by $\mathrm{CH}^*(A)=\oplus _i \mathrm{CH}^i(A)$ the graded ring $\mathrm{CH}^*(A)_{\mathrm{num}}$.

2.2 Some examples of (auto)equivalences

We denote by A an abelian surface and by ${\widehat{A}}$ its dual variety. Moreover let ${{\mathcal {P}}}$ be the normalized Poincaré line bundle on $A\times {\widehat{A}}$ so that ${{\mathcal {S}}}_A:=\Phi _{{{\mathcal {P}}}}:{\mathbf {D}}(A)\rightarrow {\mathbf {D}}({\widehat{A}})$ is an equivalence of triangulated categories [23]. The action of ${{\mathcal {S}}}_A^{\mathrm{CH}}$ swaps the first and third entry of a vector, e.g.:

$$\begin{aligned} {{\mathcal {S}}}_{A}^{\mathrm{CH}}\big (\mathrm{CH}^0(A)\big )=\mathrm{CH}^2({\widehat{A}}),\quad {{\mathcal {S}}}_{A}^{\mathrm{CH}}\big (\mathrm{CH}^2(A)\big )=\mathrm{CH}^0({\widehat{A}}), \quad \hbox {and}\quad {{\mathcal {S}}}_{A}^{\mathrm{CH}}\big (\mathrm{CH}^1(A)\big )=\mathrm{CH}^1({\widehat{A}}). \end{aligned}$$

Let now H be a line bundle on A and h be its class in $\mathrm{CH}^1(A)$. The autoequivalence $T_A(H^{\otimes n}):{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(A)$ ($n\in {\mathbf {Z}}$) defined by ${{\mathcal {F}}}\mapsto {{\mathcal {F}}}\otimes H^{\otimes n}$ acts on the numerical Chow rings as:

$$\begin{aligned} T_A(H^{\otimes n})^{\mathrm{CH}}(r,l,\chi ) = \Big (r, \, l\, +\, r\,n\,h, \, \chi \, +\, n\,l\cdot h\,+ \,r\,n^2 \, \frac{h^2}{2}\Big ). \end{aligned}$$

(2.3)

Finally, the shift functor $[1]:{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(A)$ acts on $\mathrm{CH}^*(A)$ by ${-}\,1$.

2.3 Isogenies and exponents

If A is an abelian variety over k, we denote by $n_A:A\rightarrow A$ the multiplication-by-n-map and by A[n] its kernel. We say that an elliptic curve E over k is ordinary (resp.supersingular) if $E[p](k)={\mathbf {Z}}/ p{\mathbf {Z}}$ (resp.$E[p](k)=0$) (cf. [16]). Therefore E is supersingular if and only if $p_E$ is inseparable and the j-invariant is defined over ${\mathbf {F}}_{p^2}$, the finite field with $p^2$ elements (cf. [33, Theorem V.3.1]). The exponent$\mathrm{exp} \, \varphi$ of a separable isogeny $\varphi :A\rightarrow B$ of abelian varieties is the smallest positive integer that annihilates its kernel. Finally we recall that if $\varphi :A\rightarrow B$ is an isogeny of exponent e, then there exists an isogeny $\psi :B\rightarrow A$ of exponent e such that $\psi \circ \varphi =e_A$ and $\varphi \circ \psi =e_B$ (cf. [3, Proposition 1.2.6]).

Proposition 2.3

Let $\nu :A\rightarrow B$ be a separable isogeny of exponent e and denote by $\nu ^*:\mathrm{CH}^1(B)\rightarrow \mathrm{CH}^1(A)$ the pull-back homomorphism. Then there is an inclusion of groups $e^2\mathrm{CH}^1(A)\subset \mathrm{Im}(\nu ^*)$.

Proof

Let $\mu :B\rightarrow A$ be the isogeny such that $\mu \circ \nu = e_A$ and note that $\mathrm{Im}\big (e_A^*:\mathrm{CH}^1(A)\rightarrow \mathrm{CH}^1(A) \big )\subset \mathrm{Im}(\nu ^*)$. We conclude by using [21, Remark 10.19] which shows that for any line bundle L, $e_A^*L$ is algebraically equivalent, hence numerically equivalent, to $L^{\otimes e^2}$. $\square$

Proposition 2.4

If E and F are supersingular elliptic curves and $l\ne p=\mathrm{char}(k)$ is a prime, then there exists an integer $r\gg 0$ and a separable isogeny $\xi :F\rightarrow E$ of degree $l^r$.

Proof

Since E and F are supersingular, their j-invariants are defined over ${\mathbf {F}}_{p^2}$. Moreover by [14, Corollary 78] there exists an isogeny $\xi ':F_{{\mathbf {F}}_{p^2}}\rightarrow E_{{\mathbf {F}}_{p^2}}$ of degree $l^r$ for some positive integer $r\gg 0$. Therefore we obtain our desired isogeny from $\xi '$ by extension of scalars. Finally we observe that $\xi$ is separable as the degree of every non-separable isogeny is divisible by $\mathrm{char}(k)$ [33, Corollary 2.12]. $\square$

2.4 Line bundles on a product of two elliptic curves

Let $(E,O_E)$ be an elliptic curve over k. We denote the Mumford bundle on $E\times E$ by

$$\begin{aligned} {{\mathcal {M}}}_E\; \,= \; {{\mathcal {O}}}_{E\times E}(\Delta _E)\, \otimes \, \mathrm{pr}_1^*{{\mathcal {O}}}_E(-O_E)\, \otimes \, \mathrm{pr}_2^*{{\mathcal {O}}}_E(-O_E) \end{aligned}$$

where $\Delta _E \subset E\times E$ is the diagonal divisor and $\mathrm{pr}_1$, $\mathrm{pr}_2$ are the projections of $E\times E$ onto the first and second factor respectively. Given another elliptic curve $(F,O_F)$, line bundles $L_E$ and $L_F$ on E and F respectively, and a morphism $\varphi :F\rightarrow E$, we define a line bundle on the product $E\times F$

$$\begin{aligned} L(\varphi ,L_E,L_F) \, := \, (1_E\times \varphi )^*{{\mathcal {M}}}_E \otimes \mathrm{pr}_E^*L_E\otimes \mathrm{pr}_F^*L_F \end{aligned}$$

(2.4)

where $\mathrm{pr}_E$ and $\mathrm{pr}_F$ are the projections onto E and F respectively.

Proposition 2.5

If $\varphi :F\rightarrow E$ and $\psi :F\rightarrow E$ are isogenies, then

$$\begin{aligned} \big (1_E\times (\varphi +\psi )\big )^*{{\mathcal {M}}}_E\, \simeq \, (1_E\times \varphi )^*{{\mathcal {M}}}_E\otimes (1_E\times \psi )^*{{\mathcal {M}}}_E. \end{aligned}$$

Therefore for any choice of line bundles $M_E$ and $N_E$ on E, and line bundles $M_F$ and $N_F$ on F, there are isomorphisms

$$\begin{aligned} L(\varphi +\psi ,M_E\otimes N_E,M_F\otimes N_F)\, \simeq \, L(\varphi ,M_E,M_F) \otimes L(\psi ,N_E,N_F). \end{aligned}$$

Proof

The proof is a simple application of the see-saw principle. $\square$

If $L_E,L_E'$ and $L_F,L_F'$ are line bundles on E and F respectively such that $d_E:=\deg \,L_E=\deg \, L_E'$ and $d_F:=\deg \,L_F=\deg \,L_F'$, then the classes of $L(\varphi ,L_E,L_F)$ and $L(\varphi ,L_E',L_F')$ coincide in $\mathrm{CH}^1(E\times F)$. We denote by $l(\varphi ,d_E,d_F)$ the numerical class of $L(\varphi ,L_E,L_F)$ (or $L(\varphi ,L_E',L_F')$).

Corollary 2.6

With notation as in Proposition 2.5, in $\mathrm{CH}^1(E\times F)$ there are equalities of classes

$$\begin{aligned} l(\varphi +\psi ,d_E+d'_E,d_F+d'_F) = l(\varphi ,d_E,d_F) + l(\psi ,d'_E,d'_F) \end{aligned}$$

where $d_E$ and $d_F$ are the degrees of $M_E$ and $M_F$ respectively, and $d'_E$ and $d'_F$ are the degrees of $N_E$ and $N_F$ respectively.

Finally we show that any line bundle $L\in \mathrm{Pic}(E\times F)$ can be realized as a line bundle of the form (2.4).

Proposition 2.7

For any line bundle $L\in \mathrm{Pic}(E\times F)$ there exists a morphism $\varphi :F\rightarrow E$ and line bundles $L_E\in \mathrm{Pic}(E)$ and $L_F\in \mathrm{Pic}(F)$ such that $L\simeq L(\varphi ,L_E,L_F)$.

Proof

Denote by $L_E$ the restriction of L to $E\times \{O_F\}$, and similarly let $L_F$ be the restriction of L to $\{O_E\}\times F$. Set now $L' \;:=\, L\, \otimes \mathrm{pr}_E^*L_E^{-1}\, \otimes \, \mathrm{pr}_F^* L_F^{-1}.$ We note that the restriction of $L'$ to $\{O_E\}\times F$ is trivial, while the restrictions $L'|_{E\times \{y\}}$ lie in $\mathrm{Pic}^0(E)$ for all $y\in F$. Thus by the universal property of the dual variety [26, Theorem on p. 117], there exists a unique morphism $\widetilde{\varphi }:F\rightarrow {\widehat{E}}$ such that

$$\begin{aligned} L' = (1_E\times {{\widetilde{\varphi }}})^*{{\mathcal {P}}}_E \end{aligned}$$

where ${{\mathcal {P}}}_E$ is the normalized Poincaré line bundle on $E\times {\widehat{E}}$ (namely the restrictions of ${{\mathcal {P}}}_{E}$ to $\{O_E\}\times {\widehat{E}}$ and $E\times \{O_{{{\widehat{E}}}}\}$ are trivial). Moreover we have an isomorphism ${{\mathcal {M}}}_E\simeq (1_E\times \eta )^{*}{{\mathcal {P}}}_E$ induced by the isomorphism $\eta (x)={{\mathcal {O}}}_E(x-O_E)$. Hence $L'\simeq \big (1_E\times (\eta ^{-1}{\widetilde{\varphi }}) \big )^*{{\mathcal {M}}}_E$ and the conclusion of the proposition follows by setting $\varphi =\eta ^{-1}{\widetilde{\varphi }}$. $\square$

2.5 Lifting results

Let k be a perfect field of positive characteristic p and let W(k) be the ring of Witt vectors with quotient field K. We recall that it is a complete discrete valuation ring such that K is of characteristic zero (see for instance [31, Sect. II.6]). We will denote by W both W(k) and finite extensions of W(k). If X denotes a smooth projective scheme over k, a projective lift of X over W is a flat morphism $\psi :{\mathcal {X}}\rightarrow W$ where ${\mathcal {X}}$ is a projective scheme, together with the choice of an isomorphism between the closed fiber ${\mathcal {X}}_k$ and X. Grothendieck’s existence theorem establishes that smooth curves always lift, as well as the line bundles on them. Moreover ordinary abelian varieties admit a canonical lift over W characterized by the fact that the absolute Frobenius lifts with the abelian variety (we recall that an abelian variety A is ordinary if $A[p](k)\simeq ({\mathbf {Z}}/ p{\mathbf {Z}})^{\dim A}$). We refer to [22, Appendix, Theorem 1] for the proof of the following result.

Theorem 2.8

Let A be an ordinary abelian variety over a perfect field k of positive characteristic p. Then there exists a projective lift ${{\mathcal {A}}}\rightarrow W$ of A together with a morphism $F_{{{\mathcal {A}}}}:{{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$ compatible with the Frobenius of W such that $F_{{{\mathcal {A}}}|A}$ is the absolute Frobenius $F_A$ of A. The pair $({{\mathcal {A}}},F_{{{\mathcal {A}}}})$ is called a canonical lift and is unique up to a unique isomorphism inducing the identity on A. Moreover, the restriction morphism $\mathrm{Pic}({{\mathcal {A}}})\rightarrow \mathrm{Pic}(A)$ is surjective and

$$\begin{aligned} \mathrm{Pic}({{\mathcal {A}}})_{F_{{{\mathcal {A}}}}}:=\{{{\mathcal {L}}}\in \mathrm{Pic}({{\mathcal {A}}}) \, | \, F_{{{\mathcal {A}}}}^*{{\mathcal {L}}}\simeq {{\mathcal {L}}}^{\otimes p} \} \simeq \mathrm{Pic}(A). \end{aligned}$$

Finally, if $\varphi :A\rightarrow B$ is a morphism between ordinary abelian varieties, then there exists a unique morphism ${\widetilde{\varphi }}:{{\mathcal {A}}}\rightarrow {{\mathcal {B}}}$ of canonical liftings such that $F_{{{\mathcal {B}}}}\circ \, {\widetilde{\varphi }} = \, {\widetilde{\varphi }}\circ F_{{{\mathcal {A}}}}$ and ${\widetilde{\varphi }}_{|A} = \varphi$.

Another result that we will need in the sequel is the existence of liftings of étale covers. A reference for the following theorem is [32, Sect. IX, 1.10].

Theorem 2.9

Let S be the spectrum of a complete local Noetherian ring, and let $X\rightarrow S$ be a proper S-scheme. Moreover denote by $X_0$ the closed fiber over the unique closed point of S. Then the assignment $X'\mapsto X'\times _{X}X_0$ yields an equivalence between the category of finite étale coverings of X and the category of finite étale coverings of $X_0$.

2.6 Moduli spaces

Let A be an abelian surface defined over a field k and let $h\in \mathrm{NS}(A)$ be the class of an ample line bundle. Given a vector $v=(r,l,\chi ) \in \mathrm{CH}^*(A)$ with integral coefficients, we consider the moduli space ${{\mathcal {M}}}_h(v)$ of Gieseker-semistable sheaves with Mukai vector v, where stability is computed with respect to h. We want to show that, under certain assumptions, these spaces are irreducible and are Fourier–Mukai partners of A. We will need the following criterion for fully faithfulness:

Theorem 2.10

[19, Theorem 2.6] A Fourier–Mukai functor $\Phi _{{{\mathcal {U}}}}:{\mathbf {D}}(M)\rightarrow {\mathbf {D}}(A)$ between the derived categories of two smooth abelian surfaces over k is fully faithful if the following three conditions are satisfied:

• (i) $\mathrm {Hom}^i(\Phi _{{\mathcal {U}}}(k(x)),\Phi _{{\mathcal {U}}}(k(y))=0$ if $0>i$ or $i>\dim X$ or when $x\ne y$;

• (ii) $\mathrm {Hom}^0(\Phi _{{\mathcal {U}}}(k(x)),\Phi _{{\mathcal {U}}}(k(x))=k$ for all $x\in M$;

• (iii) $\Phi _{{{\mathcal {U}}}^\vee [2]}\circ \Phi _{{{\mathcal {U}}}}(k(x))\simeq k(x)$ for some $x\in M$.

Now we can turn to the proof of the following:

Theorem 2.11

If $r>0$ and $\chi$ are coprime integers, then every Gieseker-semistable sheaf on A with Mukai vector v is Gieseker-stable. Moreover, if in addition $\langle v,v \rangle _A=0$, then ${{\mathcal {M}}}_h(v)$ is a smooth irreducible projective variety of dimension two which admits a universal family ${{\mathcal {U}}}$ on ${{\mathcal {M}}}_h(v)\times A$. Furthermore, ${{\mathcal {M}}}_h(v)$ has trivial canonical bundle and the Fourier–Mukai functor $\Phi _{{{\mathcal {U}}}}:{\mathbf {D}}({{\mathcal {M}}}_h(v))\rightarrow {\mathbf {D}}(A)$ induces an equivalence of derived categories.

Proof

The first assertion follows by [8, Remark 4.6.8] (cf. also [8, Remark 6.1.9]), while the second follows by [24, Corollary 0.2]. The existence of a universal sheaf follows by [25, Theorem A.6]. We remark, as noted by Lieblich–Olsson [17, Remark 3.17], that while the results of [25] are just stated for characteristic 0, the argument is true also in positive characteristic. The only tricky point in the algebraic setting is determining the non-emptiness of these spaces, which can be done using the work of Langton [15, Theorem on p. 99].

To prove the irreducibility of ${{\mathcal {M}}}_h(v)$, we use an argument of Mukai. Let $M\subseteq {{\mathcal {M}}}_h(v)$ be an irreducible component. The smoothness of ${{\mathcal {M}}}_h(v)$ implies that M is also a connected component of the moduli space. Suppose that $M\ne {{\mathcal {M}}}_h(v)$. Let ${\mathcal {U}}$ be the universal family of ${{\mathcal {M}}}_h(v)$ restricted to $M\times A$. We can construct the Fourier–Mukai functor

$$\begin{aligned} \Phi _{{{\mathcal {U}}}^{\vee }[2]}:{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(M). \end{aligned}$$

(2.5)

Observe that we have an isomorphism of functors $\Phi _{{{\mathcal {U}}}^{\vee }[2]}(-)\simeq {\mathbf {R}}p_{1*}{\mathbf {R}}{\mathcal {H}}om({{\mathcal {U}}},p_2^*(-))[2]$. This functor sends any stable sheaf on A whose corresponding point lies on $M\subset {{\mathcal {M}}}_h(v)$ to a skyscraper sheaf at that point on M, while it sends all the stable sheaves on A that are not on M to zero (see for example [13, Proof of Theorem 2.2]—the proof uses only that there are no nontrivial homs between stable sheaves of the same slope so it works also in positive characteristic). On the other hand, for any sheaf ${\mathcal {F}}$ on M, the Mukai vector of $\Psi _{{\mathcal {U}}}({\mathcal {F}})$ only depends on the Mukai vector of ${\mathcal {F}}$ as it is obtained by convoluting $v({\mathcal {F}})$ with $v({{\mathcal {U}}}^\vee )$. This leads to a contradiction as skyscraper sheaves and the zero object have different Mukai vectors.

Finally, we only have to show that $\Phi _{{{\mathcal {U}}}}$ is an equivalence. We will prove that it is fully faithful using Theorem 2.10, and then conclude by [7, Proposition 7.6]. We remark that, even though Chapter 7 of [7] is in characteristic 0, this proposition uses only the fully-faithfulness of $\Phi _{{{\mathcal {U}}}}$ and some general results about k-linear categories and adjoint functors, so it works in our setting.

By [25, Proposition 3.12] the universal family ${{\mathcal {U}}}$ is strongly simple. In particular we have that

• (i) $\mathrm {Hom}^i(\Phi _{{\mathcal {U}}}(k(x)),\Phi _{{\mathcal {U}}}(k(y))=0$ if $0>i$ or $i>\dim X$ or when $x\ne y$;

• (ii) $\mathrm {Hom}^0(\Phi _{{\mathcal {U}}}(k(x)),\Phi _{{\mathcal {U}}}(k(x))=k$.

So we just need to check that there is a skyscraper sheaf such that

$$\begin{aligned} \Phi _{{{\mathcal {U}}}^{\vee }[2]}\circ \Phi _{{{\mathcal {U}}}}(k(x))\simeq k(x). \end{aligned}$$

By the definition of universal family the functor $\Phi _{{{\mathcal {U}}}}$ sends a skyscraper sheaf k(x) to a stable sheaf ${{\mathcal {U}}}_x\in {{\mathcal {M}}}_h(v)$. The above discussion implies that ${\mathcal {E}}:=\Phi _{{{\mathcal {U}}}^{\vee }[2]}({{\mathcal {U}}}_x)$ is a skyscraper sheaf on ${{\mathcal {M}}}_h(v)$. Since $\Phi _{{{\mathcal {U}}}^\vee [2]}$ is the left adjoint of $\Phi _{{{\mathcal {U}}}}$, the strong simplicity of ${{\mathcal {U}}}$ implies that $\mathrm {Hom}_{{\mathbf {D}}({{\mathcal {M}}}_h(v))}({\mathcal {E}}, k(x))\simeq k$, and so we are finished. $\square$

2.7 Relative moduli spaces

We also need to consider relative moduli spaces of Gieseker-semistable sheaves on a projective lift $f:{{\mathcal {A}}}\rightarrow W$ of an abelian surface A over the ring of Witt vectors. Let h be the class of an ample line bundle as before, and let ${\widetilde{h}}$ be a lifting of h to ${{\mathcal {A}}}$. Let $v=(r,l,\chi ) \in \mathrm{CH}^*(A)$ be a vector with integral coefficients such that l is the class of a line bundle L that lifts to a line bundle ${\widetilde{L}}$ on ${{\mathcal {A}}}$. Moreover set ${\widetilde{v}}=(r,{\widetilde{l}},\chi )$ where ${\widetilde{l}}$ is the class of ${\widetilde{L}}$. By [20, Theorem 0.7] (or [15, Theorem 0.2]) there exists a projective scheme ${{\mathcal {M}}}_{{{\mathcal {A}}}/W}({\widetilde{v}})\rightarrow W$ of finite type that is a coarse moduli space for the functor of families of pure Gieseker-semistable sheaves with Mukai vector v on the geometric fibers of f (where stability is computed with respect to ${\widetilde{h}}$). Moreover, there exists an open subscheme ${{\mathcal {M}}}^s_{{{\mathcal {A}}}/W}({\widetilde{v}})\subset {{\mathcal {M}}}_{{{\mathcal {A}}}/W}({\widetilde{v}})$ that is a coarse moduli space for the subfunctor of families of pure Gieseker-stable sheaves. Thus, if $(r,\chi )=1$ (i.e. every Gieseker-semistable sheaf is Gieseker-stable), then we have ${{\mathcal {M}}}^s_{{{\mathcal {A}}}/ W}({\widetilde{v}})={{\mathcal {M}}}_{{{\mathcal {A}}}/W}({\widetilde{v}})$. Note that if we denote the closed fiber of f by $A_k$ and the geometric generic fiberby $A_{\eta }$, then there are isomorphisms

$$\begin{aligned} {{\mathcal {M}}}_{{{\mathcal {A}}}/W}({\widetilde{v}})_{|A_k} \simeq {{\mathcal {M}}}_h(v)\quad \hbox { and }\quad {{\mathcal {M}}}_{{{\mathcal {A}}}/W}({\widetilde{v}})_{|A_{\eta }} \simeq {{\mathcal {M}}}_{h_{\eta }}(v_{\eta }) \end{aligned}$$

where ${{\mathcal {M}}}_{h_{\eta }}(v_{\eta })$ is the moduli space of pure Gieseker-stable sheaves with vector $v_{\eta }=(r,{\tilde{l}}_{|A_{\eta }}, \chi )$ on $A_{\eta }$, and $h_{\eta }$ is the restriction of ${\widetilde{h}}$ to $A_{\eta }$. The smoothness of the moduli space implies that ${\widetilde{f}}:{{\mathcal {M}}}_{{{\mathcal {A}}}/W}({\widetilde{v}})\rightarrow W$ is formally smooth and of finite type, and hence flat. So, with a choice of isomorphism ${{\mathcal {M}}}_{{{\mathcal {A}}}/W}({\widetilde{v}})_{|A_k} \simeq {{\mathcal {M}}}_h(v)$, it is a lift of ${{\mathcal {M}}}_h(v)$.

3 Filtered derived equivalences

An equivalence $\Phi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(B)$ of derived categories of abelian surfaces is filtered if

$$\begin{aligned} \Phi ^{\mathrm{CH}} (0, \, 0, \, 1 \big ) = (0, \, 0, \,1). \end{aligned}$$

In [17, Theorem 6.1] the authors prove that if two K3 surfaces have a filtered equivalence between them, then they are isomorphic. The proof of this statement is quite involved and uses deformation theory of complexes in order to lift a derived equivalence of K3 surfaces in positive characteristic to an equivalence of K3 surfaces in characteristic zero. Here we notice that a filtered equivalence of abelian surfaces still induces an isomorphism. As the kernel of an equivalence of abelian varieties is a sheaf (up to shift), its proof turns out to be rather simple.

Proposition 3.1

Let $\Phi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(B)$ be a filtered equivalence between the derived categories of two abelian surfaces. Then there exists an isomorphism $f:A\rightarrow B$ and a line bundle L on $A\times B$ such that $\Phi$ is isomorphic to $(-\otimes L)\circ f_*$ up to shift. In particular A and B are isomorphic.

Proof

Equivalences of derived categories of abelian varieties send (up to shift) structure sheaves of points ${{\mathcal {O}}}_x$ to sheaves. This is proved in [5, Lemma 10.2.6] in characteristic zero, but its proof extends to positive characteristic without any change. Hence we can suppose that $\Phi ({{\mathcal {O}}}_x)$ is a sheaf with Mukai vector (0, 0, 1), so it is itself a skyscraper sheaf. Since the argument holds for all points x in A, the proposition follows by [7, Corollary 5.23]. $\square$

We now prove Theorem 1.2 of the introduction, which relies on the following technical proposition.

Proposition 3.2

Let $\Phi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(B)$ be an equivalence between the derived categories of two abelian surfaces. Then there exists an equivalence $\Psi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(C)$ where $C\in \{B,{\widehat{B}}\}$ such that the vector

$$\begin{aligned} \Psi ^{\mathrm{CH}}(0, \,0, \,1) := (r, \, l, \, \chi ) \end{aligned}$$

satisfies the following conditions:

• (i) r is positive;

• (ii) l is the class of an ample line bundle on C;

• (iii) r is coprime with $\chi$.

Moreover we have $C=B$ (resp. $C={{\widehat{B}}}$) if the first component of $\Phi ^{\mathrm{CH}}(0,0,1)$ is nonzero (resp. zero).

Proof

Set

$$\begin{aligned} v_0 := \Phi ^{\mathrm{CH}}(0,0,1) \; =\; (r_0, \, l_0, \, \chi _0). \end{aligned}$$

We split our argument in several steps.

Step 1 Given an equivalence $\Phi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(B)$ as in the statement, there exists an equivalence $\Psi _1:{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(C)$ with $C\in \{B,{\widehat{B}}\}$ such that the first entry of the vector

$$\begin{aligned} v_1:=\Psi _1^{\mathrm{CH}}(0,0,1)=(r_1, \, l_1, \, \chi _1) \end{aligned}$$

is positive. Moreover we have $C = B$ if $r_0\ne 0$, and $C={{\widehat{B}}}$ otherwise.

If $r_0>0$ there is nothing to prove and we simply set $\Psi _1=\Phi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(B)$. If $r_0<0$, we set $\Psi _1:=\Phi \circ [1] :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(B)$ in order to make $r_0$ positive. Suppose now that $r_0=0$ and $\chi _0\ne 0$. Then it is enough to set $\Psi _1:={{\mathcal {S}}}_B \circ \Phi$ if $\chi _0>0$, and $\Psi _1:={{\mathcal {S}}}_B\circ \Phi [1]$ if $\chi _0<0$. Observe that both these equivalences are between ${\mathbf {D}}(A)$ and ${\mathbf {D}}({\widehat{B}})$. So we are left with the case $r_0=\chi _0=0$. Let $\Phi ^\mathrm{CH}(1,0,0):=w_0=(s_0,b_0,\xi _0)$. By noting that $v({{\mathcal {O}}}_x)=(0,0,1)$ for any point $x\in B$, and $v({{\mathcal {O}}}_B)=(1,0,0)$, by (2.2) we find that $\langle v_0, w_0\rangle _B=l_0\cdot b_0=1$. Hence, if $B_0$ is a line bundle with class $b_0$, then the composition $\big (T_B(B_0)\circ \Phi \big )^{\mathrm{CH}}$ sends (0, 0, 1) to $(0, l_0, 1)$ as showed in (2.3). Thus we set $\Psi _1:={{\mathcal {S}}}_B\circ T_B(B_0)\circ \Phi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}({\widehat{B}})$ and we have the desired equivalence.

Step 2 Given an equivalence $\Psi _1:{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(C)$ as in the previous step, there exists an equivalence $\Psi _2:{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(C)$ so that in $v_2:=\Psi _2^{\mathrm{CH}}(0,0,1)=(r_2,l_2,\chi _2)$, $r_2>0$ and $\chi _2$ is coprime with $r_2$.

Let $w_1:=\Psi ^{\mathrm{CH}}_1(1,0,0)=(s_1,b_1,\xi _1)$, so $\langle v_1, w_1\rangle _C=1$ and

$$\begin{aligned} I - r_1 \, \xi _1 \, -\, \chi _1 \, s_1 = 1\quad \hbox { where }\quad I := l_1\cdot b_1. \end{aligned}$$

(3.1)

By (3.1), it is possible to choose an n so that $\chi _1+nI$ is relatively prime with $r_1$. Let $B_1$ be a line bundle with numerical class $b_1$. By (2.3) the homomorphism $\big ( T_C(B_1^{\otimes n})\circ \Psi _1\big )^{\mathrm{CH}}$ sends (0, 0, 1) to

$$\begin{aligned} v_2 := (r_2, \, l_2, \, \chi _2)\; = \, \left( r_1, \, l_1 \, +\, r_1 \, n\, b_1, \, \chi _1 + n \, I\, +\, r_1 \,n^2 \, \frac{b_1^2}{2}\right) . \end{aligned}$$

Our choice of n ensures that $r_2$ and $\chi _2$ are relatively prime.

Step 3 Given an equivalence $\Psi _2:{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(C)$ as in the previous step, there exists an equivalence $\Psi _3:{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(C)$ satisfying the conditions of the proposition.

Let $\Theta$ be an ample line bundle with class $\theta \in \mathrm{CH}^1(C)$. For any integer $d>0$, the equivalence $T_C(\Theta ^{\otimes (r_1\,d)})\circ \Psi _2$ sends (0, 0, 1) to

$$\begin{aligned} \left( r_1, \, l_1 + r_1 \, n \, b_1 + r_1^2 \, d\, \theta , \, \chi _1 + n \, I\, +\, r_1 \,n^2 \, \frac{b_1^2}{2} \, +\, r_1 \,d \,\big (\theta \cdot (l_1 + r_1 \,n \,b_1) \big ) \, +\, r_1^3 \, d^2 \, \frac{\theta ^2}{2}\right) . \end{aligned}$$

Choose d large enough so that the second component is an ample class and set $\Psi _3^{\mathrm{CH}}:=T_C(\Theta ^{\otimes (r_1\,d)})\circ \Psi _2$. The first component of $v_3:=\Psi _3^{\mathrm{CH}}(0,0,1)$ is positive by the previous steps, and the third component of $v_3$ is congruent to $\chi _2$ modulo $r_1$. $\square$

Theorem 3.3

Let A be an abelian surface and let $\Phi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(Y)$ be an equivalence of derived categories of smooth projective varieties. Then Y is an abelian surface. Moreover, A is isomorphic to a moduli space of Gieseker-stable sheaves on either Y, or its dual ${\widehat{Y}}$, according to whether the rank component of $\Phi ^{\mathrm{CH}}(0,0,1)$ is non-zero, or zero, respectively.

Proof

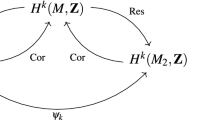
By general theory Y has trivial canonical bundle and Kodaira dimension 0. Let $l\ne p$ be a prime and consider the $\ell$-adic cohomology groups $H^i_{\acute{e}t} (Y,{\mathbf {Q}}_{\ell })$. By [9, Lemma 3.1] the equivalence $\Phi$ induces an isomorphism

$$\begin{aligned} H^1_{\acute{e}t} (Y,{\mathbf {Q}}_{\ell }) \; \oplus \; H^3_{\acute{e}t} (Y,{\mathbf {Q}}_{\ell })(2) \; \simeq \; H^1_{\acute{e}t} (A,{\mathbf {Q}}_{\ell }) \; \oplus \; H^3_{\acute{e}t} (A,{\mathbf {Q}}_{\ell })(2) \end{aligned}$$

which leads to the equality of Betti numbers:

$$\begin{aligned} b_1(Y) \;= \;b_1(A) = 4. \end{aligned}$$

Since Y is a smooth, projective surface with Kodaira dimension 0 and $b_1=4$, it is isomorphic to an abelian surface (See Theorem 6 and the table on p. 25 of [4]).

By Proposition 3.2 we may fix an equivalence $\Psi :{\mathbf {D}}(A)\rightarrow {\mathbf {D}}(C)$ with $C\in \{Y,{\widehat{Y}}\}$ such that in the vector

$$\begin{aligned} v := \Psi ^{\mathrm{CH}}(0,0,1) = (r, \, l, \, \chi ), \end{aligned}$$

the rank component r is positive, the class l is ample, and $\chi$ is coprime with r. Moreover, $C=Y$ if the rank component of $\Phi ^{\mathrm{CH}}(0,0,1)$ is non-zero, and $C={\widehat{Y}}$ otherwise.

By Theorem 2.11 there exists a universal family ${{\mathcal {U}}}$ on ${{\mathcal {M}}}_l(v)\times C$, which induces an equivalence

$$\begin{aligned} \Phi _{{{\mathcal {U}}}}\,: \,{\mathbf {D}}({{\mathcal {M}}}_l(v))\rightarrow {\mathbf {D}}(C) \end{aligned}$$

such that $\Phi ^{\mathrm{CH}}_{{{\mathcal {U}}}}(0,0,1) = v.$ As the composition $\big (\Phi _{{{\mathcal {U}}}}^{-1}\circ \Psi \big )^{\mathrm{CH}}$ sends (0, 0, 1) to (0, 0, 1), by Proposition 3.1 we get $A\simeq {{\mathcal {M}}}_l(v_l)$. $\square$

4 FM partners of canonical covers of hyperelliptic surfaces

In this and the next section, we will work, unless otherwise specified, under the assumption that the characteristic p of the base field is bigger than 3.

We denote the set of Fourier–Mukai partners of a smooth projective variety X by

$$\begin{aligned} \mathrm{FM}(X) := \{\, Y \; | \; Y\hbox { is a smooth projective variety with }\, {\mathbf {D}}(Y)\simeq {\mathbf {D}}(X)\}_{/\simeq }. \end{aligned}$$

In the case of an abelian variety A, we say that its set of Fourier–Mukai partners is trivial if $\mathrm{FM}(A) = \{A,{\widehat{A}}\}$.

A hyperelliptic surface over an algebraically closed field k of positive characteristic $p>3$ is a smooth projective minimal surface X with $K_X\equiv 0$, $b_2(X)=2$, and such that each fiber of the Albanese map is a smooth elliptic curve (cf. [1, Sect. 10]). These surfaces can be described as quotients $(E\times F)/G$ of two elliptic curves E and F by a finite group G. The group G acts on E by translations, and on F in a way such that $F/G\simeq {\mathbf {P}}^1$. Moreover, there are only a finite number of possibilities for the action of G on $E\times F$, which have been classified by Bagnera–De Franchis [1, 10.27].

By [1, Sect. 9.3] the order n of the canonical bundle of X is finite with $n=2,3,4,6$. Therefore we can consider the canonical cover$\pi :{\widetilde{X}}\rightarrow X$ of the surface X, which is the étale cyclic cover associated to the canonical bundle $\omega _X$. The degree of $\pi$ is the order n of $\omega _X$, and in addition $\pi$ comes equipped with an action of the cyclic group that realizes X as the quotient ${\widetilde{X}}/({\mathbf {Z}}/n{\mathbf {Z}})$. According to Bagnera–De Franchis’ list [1, 10.27], the canonical cover ${\widetilde{X}}$ of an arbitrary hyperelliptic surface $X=(E\times F)/G$ is an abelian surface that sits inside a tower of surfaces

$$\begin{aligned} E\times F \; {\mathop {\longrightarrow }\limits ^{\pi '}} \; {\widetilde{X}}\; {\mathop {\longrightarrow }\limits ^{\pi }}\; X, \end{aligned}$$

where $\pi '$ is an étale cyclic cover of degree at most three. Moreover, if $\pi '$ has degree three, then F admits an automorphism group of order three and has j-invariant equals to zero. Therefore the dual morphism $\widehat{\pi '}$ realizes the dual of ${\widetilde{X}}$ as one of the following varieties: (i) the product $E\times F$, (ii) an étale cyclic cover of $E\times F$ of degree two, or (iii) an étale cyclic cover of $E\times F$ of degree three such that F has an automorphism group of order three.

4.1 The work of Sosna

In [34, Theorem 1.1] the author proves that the set of Fourier–Mukai partners of the canonical cover of a complex hyperelliptic surface is trivial. By using Bagnera–De Franchis’ classification, Sosna’s theorem boils down to proving the following result concerning derived equivalences of special abelian surfaces.

Theorem 4.1

(Sosna) Let E and F be complex elliptic curves and let A be a complex abelian surface. Then the set $\mathrm{FM}(E\times F)$ is trivial. Moreover, if $E\times F\rightarrow A$ is a degree two étale cyclic cover, then $\mathrm{FM}(A)$ is trivial. Finally, the same conclusion holds if $E\times F\rightarrow A$ is a degree three étale cyclic cover and $\mathrm{rk \, NS}(A) \in \{2,4\}$.

In view of Theorem 2.9 we prefer to work with étale covers rather than quotients. Thus we reformulate Sosna’s theorem in the following version.

Proposition 4.2

Given a complex abelian surface A, then the set $\mathrm{FM}(A)$ is trivial in the following cases:

• (i) A is isomorphic to the product $E\times F$ of two elliptic curves;

• (ii) A is a degree two étale cyclic cover of a product $E\times F$ of two elliptic curves;

• (iii) A is a degree three étale cyclic cover of a product $E\times F$ of two elliptic curves and $\mathrm{rk \, NS}(A) \in \{2,4\}$.

Proof

If $A\rightarrow E\times F$ is a cover of degree one, two, or three, then the dual isogeny $E\times F\rightarrow {{\widehat{A}}}$ realizes ${\widehat{A}}$ as a quotient of two elliptic curves. Then by Theorem 4.1 we conclude that $\mathrm{FM}({\widehat{A}})$ is trivial. As $\mathrm{FM}(A)=\mathrm{FM}({\widehat{A}})$ and $\mathrm{rk\, NS}(A)=\mathrm{rk \, NS}({{\widehat{A}}})$, the proposition follows at once. $\square$

As an application of Proposition 4.2, we deduce some further finitiness results that will be useful towards the proof of Theorem 1.1.

Proposition 4.3

If $\varphi :A\rightarrow E\times F$ is an isogeny with $\mathrm{deg} \, \varphi =8$ and $\mathrm{exp} \, \varphi =2$, then $\mathrm{FM}(A)$ is trivial. The same conclusion holds if $\mathrm{rk\, NS}(A) \in \{2,4\}$, $\mathrm{deg}\, \varphi =27$ and $\mathrm{exp}\,\varphi = 3$.

Proof

We show that the dual abelian variety ${\widehat{A}}$ satisfies the hypotheses of Proposition 4.2. The result will follow as $\mathrm{FM}(A)=\mathrm{FM}({\widehat{A}})$. Let q be either 2 or 3 and consider an isogeny $\psi :E\times F\rightarrow A$ of exponent q such that $\psi \circ \varphi = q_A$ (recall that $q_A$ denotes the multiplication-by-q-map on A). As $\mathrm{deg} \, q_A=q^4$ and $\mathrm{deg}\, \varphi =q^3$, we deduce that $\mathrm{deg}\,\psi =q$. Hence the dual isogeny ${\widehat{\psi }}$ is a cyclic cover of $E\times F$ of order q. The second statement follows as $\mathrm{rk\, NS}(A) = \mathrm{rk\, NS}({\widehat{A}})$. $\square$

4.2 Strategy of the proof of Theorem 1.1

Since an abelian surface and its dual have the same Fourier–Mukai partners, the following theorem implies Theorem 1.1.

Theorem 4.4

Let A be an abelian surface over an algebraically closed field of characteristic $p>0$. Then $\mathrm{FM}(A)$ is trivial in the following cases:

• (i) A is isomorphic to the product $E\times F$ of two elliptic curves;

• (ii) $p>2$ and A is a degree two étale cyclic cover over the product $E\times F$ of two elliptic curves;

• (iii) $p>3$ and A is a degree three étale cyclic cover over the product $E\times F$ of two elliptic curves such that F admits an automorphism of order 3.

In order to prove the previous theorem, we will consider the following set of hypotheses

Setting 4.5

We denote by E and F two elliptic curves over an algebraically closed field k of characteristic $p>0$. Moreover we set $\nu :A\rightarrow E\times F$ to be either an isomorphism of abelian surfaces, or an étale cyclic cover of degree $d_{\nu }=2,3$ (as in the hypotheses of Theorem 4.4). Finally we assume that $p>\mathrm{deg}\, \nu$.

Remark 4.6

Since the exponent of an isogeny divides its degree, the exponent of the isogeny $\nu$ of Setting 4.5 is either 1 if $\nu$ is an isomorphism, or $d_{\nu }$ otherwise. Now let $\mu :E\times F\rightarrow A$ be an isogeny of exponent $d_{\nu }$ such that $\mu \circ \nu =(d_{\nu })_A$. Then the dual isogeny ${\widehat{\mu }}:{\widehat{A}}\rightarrow E\times F$ is either an isomorphism, or else its degree and exponent satisfy $(\mathrm{deg}\, {\widehat{\mu }},\mathrm{exp} \, {\widehat{\mu }}) = (d_{\nu }^3,\,d_{\nu }).$

As an application of Theorem 2.9 we deduce that both the isogenies $\nu$ and ${\widehat{\mu }}$ of Setting 4.5 and Remark 4.6 lift to the ring of Witt vectors. In the following result we check that their degrees and exponents remain unchanged when passing from the special fiber to the general fiber.

Proposition 4.7

Let E and F be elliptic curves and $\varphi :A\rightarrow E\times F$ be an étale isogeny of abelian surfaces with degree relatively prime with p. If ${{\mathcal {E}}}\rightarrow R$ and ${{\mathcal {F}}}\rightarrow R$ are projective lifts of ${{\mathcal {E}}}$ and ${{\mathcal {F}}}$ over an Henselian local ring R with residue field k, then there exists a projective lift ${{\mathcal {A}}}\rightarrow R$ of A and an isogeny $\varphi _R :{{\mathcal {A}}}\rightarrow {{\mathcal {E}}}\times _R{{\mathcal {F}}}$ such that $\varphi _R$ lifts $\varphi$ and its restriction $\varphi _{\eta }:A_{\eta }\rightarrow E_{\eta }\times F_{\eta }$ to the geometric general fibers is an isogeny with $\mathrm{deg} \, \varphi _{\eta }=\mathrm{deg}\, \varphi$ and $\mathrm{exp} \, \varphi _{\eta }=\mathrm{exp}\, \varphi$

Proof

By Theorem 2.9 there is a projective lift ${{\mathcal {A}}}\rightarrow R$ of A and an étale cover $\varphi _R:{{\mathcal {A}}}\rightarrow {{\mathcal {E}}}\times _{R}{{\mathcal {F}}}$ that specializes to $\varphi$. Up to composing $\varphi _R$ with a translation of ${{\mathcal {E}}}\times _{R}{{\mathcal {F}}}$, we can suppose that $\varphi _R$ is a homomorphism of groups. We are going to prove that the restriction of $\varphi _R$ to the geometric generic fiber of ${{\mathcal {A}}}$ is an isogeny $\varphi _{\eta } :A_{\eta }\rightarrow E_{\eta }\times F_{\eta }$ such that $\mathrm{deg}\,\varphi _{\eta }=\mathrm{deg}\, \varphi$. To see this we notice that the kernel ${{\mathcal {K}}}$ of $\varphi _R$ is a finite étale group over R and moreover, as $\varphi$ is separable, we have

$$\begin{aligned} \mathrm{deg}\, \varphi _{\eta }= \big |\mathrm{ker}\,\varphi _{\eta } \big |= \big |{{\mathcal {K}}}_{\eta } \big |= \big |{{\mathcal {K}}}_{k} \big | = \big |\mathrm{ker}\, \varphi \big |=\mathrm{deg}\, \varphi \end{aligned}$$

where ${{\mathcal {K}}}_k$ is the closed fiber and ${{\mathcal {K}}}_{\eta }$ is the geometric generic fiber. In addition, since ${{\mathcal {K}}}$ is a finite étale group scheme over R, the closed fiber is killed by multiplication by n if, and only if, the same is true for the geometric generic fiber. So we have also equality of the exponents. $\square$

We will deduce Theorem 4.4 from the following technical proposition.

Proposition 4.8

Assume the hypotheses of Setting 4.5 and let $\Phi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(A)$ be an equivalence of derived categories of abelian surfaces. Suppose that there exists an equivalence $\Psi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(C)$ with $C\in \{A,{\widehat{A}} \}$ such that the Mukai vector

$$\begin{aligned} v\, := \, (r, \, l, \, \chi ) = \Psi ^{\mathrm{CH}}(0, \, 0, \, 1) \end{aligned}$$

satisfies the following conditions:

$(E_1)$:

r is positive;

$(E_2)$:

the class $l\,\in \mathrm{CH}^1(C)$ is is ample;

$(E_3)$:

$\chi$ is coprime with r.

Set $\lambda =\nu$ if $C=A$, and $\lambda ={\widehat{\mu }}$ otherwise (see Remark 4.6). In addition assume that there exist projective lifts ${{\mathcal {E}}}\rightarrow W$ and ${{\mathcal {F}}}\rightarrow W$ of E and F over a finite ramified extension of the ring of Witt vectors respectively such that the following conditions hold:

$(A_1)$:

If we let $\lambda _W:{{\mathcal {C}}}\rightarrow {{\mathcal {E}}}\times _W{{\mathcal {F}}}$ be the lift of $\lambda$ determined by Proposition 4.7, and let L an ample line bundle on C with numerical class l, then L lies in the image of the restriction map

$$\begin{aligned} \rho {:} \, \mathrm{Pic}({{\mathcal {C}}}) \, \rightarrow \, \mathrm{Pic}(C). \end{aligned}$$

$(A_2)$:

If $\mathrm{deg} \, \nu = 3$ and F admits an automorphism of order three, then $\mathrm{rk \, CH}^1({{\mathcal {C}}}_{\eta })\in \{2,4\}$ where ${{\mathcal {C}}}_{\eta }$ is the geometric generic fiber of ${\mathcal {C}}\rightarrow W$.

Then B is either isomorphic to C or ${\widehat{C}}$. In particular we have that $\mathrm{FM}(A)$ is trivial.

Proof

We divide our argument in several steps.

Step 1. We first prove that there exists a projective lift ${{\mathcal {B}}}\rightarrow W$ of B such that the geometric generic fiber ${{\mathcal {B}}}_{\eta }$ is derived equivalent to ${{\mathcal {C}}}_{\eta }$. Let L be an ample line bundle on C with class l. Then Theorem 3.3 implies that B is isomorphic to a moduli space ${{\mathcal {M}}}_{l}(v)$ of Gieseker-stable shaves with Mukai vector $v=(r,l,\chi )\in \mathrm{CH}^*(C)$. Now consider a preimage ${\widetilde{L}}$ of L under $\rho$ as in $(A_1)$ and the relative moduli space

$$\begin{aligned} {{\mathcal {M}}}_{{\widetilde{l}}}({\widetilde{v}})\rightarrow W, \end{aligned}$$

where ${\widetilde{v}}_l:=(r,{\widetilde{l}},\chi )$ and ${\widetilde{l}}$ is the class of ${\widetilde{L}}$. As discussed in Sect. 2.7, this is a projective lift of B and the geometric generic fiber ${{\mathcal {M}}}_{\eta }$ is a moduli space of Gieseker-stable sheaves on ${{\mathcal {C}}}_{\eta }$ with Mukai vector $v_{\eta }=(r,{\widetilde{l}}_{|{{\mathcal {C}}}_{\eta }},\chi )$. Therefore as discussed in Theorem 2.11, the conditions (E1), (E3), and $\langle v_{\eta },v_{\eta } \rangle _{{\mathcal {C}}_{\eta }}=0$ imply that ${{\mathcal {M}}}_{\eta }$ is an abelian surface. In addition there exists a universal family ${{\mathcal {U}}}_{\eta }$ on ${{\mathcal {M}}}_{\eta }\times {{\mathcal {C}}}_{\eta }$ that induces an equivalence $\Phi _{{{\mathcal {U}}}}:{\mathbf {D}}({{\mathcal {C}}}_{\eta })\rightarrow {\mathbf {D}}({{\mathcal {M}}}_{\eta })$.

Step 2. Now we prove that under the assumptions of Theorem 4.4 the abelian surface ${{\mathcal {C}}}_{\eta }$ is isomorphic to either ${{\mathcal {M}}}_{\eta }$ or its dual $\widehat{{{\mathcal {M}}}_{\eta }}$. By the Lefschetz principle we can suppose that the abelian surface C is defined over a subfield of the complex numbers ${\mathbf {C}}$ and therefore that ${{\mathcal {C}}}_{\eta }$ is defined over ${\mathbf {C}}$. Suppose first that $\nu :A\rightarrow E\times F$ is an isomorphism. Then both $\lambda$ and $\lambda _W$ are isomorphisms and therefore so is the restriction $\lambda _{\eta } :{{\mathcal {C}}}_{\eta } \rightarrow {{\mathcal {E}}}_{\eta }\times {{\mathcal {F}}}_{\eta }$ of $\lambda _W$ to the geometric generic fibers. As a product of elliptic curves has no non-trivial Fourier–Mukai partners (Theorem 4.1), there is an isomorphism ${{\mathcal {C}}}_{\eta }\simeq {{\mathcal {M}}}_{\eta }$.

Suppose now that $\nu :A\rightarrow E\times F$ is a degree two cyclic cover. By Remark 4.6 we have $(\mathrm{deg} \, \lambda ,\mathrm{exp} \, \lambda )\in \{(2,2),(8,2)\}$ and by Proposition 4.7 we have $(\deg \, \lambda _{\eta }, \mathrm{exp} \, \lambda _{\eta })=(\deg {\lambda },\mathrm{exp}\, \lambda )$. Therefore by Propositions 4.2 and 4.3 we deduce that either ${{\mathcal {C}}}_{\eta }\simeq {{\mathcal {M}}}_{\eta }$ or ${{\mathcal {C}}}_{\eta }\simeq \widehat{{{\mathcal {M}}}_{\eta }}$. The case when $\nu$ has degree three follows similarly by using the condition $(A_2)$.

Step 3. The argument of [17, Lemma 6.5] (based on a result of Matsusaka–Mumford) proves that the isomorphism ${{\mathcal {C}}}_{\eta } \simeq {{\mathcal {M}}}_{\eta }$ (resp.${{\mathcal {C}}}_{\eta }\simeq \widehat{{{\mathcal {M}}}_{\eta }}$) between the geometric generic fibers of the two liftings induces an isomorphism $C\simeq B$ (resp.$C\simeq {\widehat{B}}$) between the closed fibers. This immediately yields that either $B\simeq A$ or $B\simeq {\widehat{A}}$, and hence that $\mathrm{FM}(A)$ is trivial. $\square$

5 Finding a suitable equivalence

In this section we finish the proof of Theorem 1.1. According to Proposition 4.8, we only need to verify its hypotheses. We work under the hypotheses of Setting 4.5 and assume that the abelian surface B is a Fourier–Mukai partner of A. In the following we will examine two cases: (a) at least one of the two elliptic curves E or F is ordinary, and (b) both E and F are supersingular.

The following two propositions show the existence of an equivalence $\Psi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(C)$ satisfying the hypotheses $(E_1)$, $(E_2)$ and $(E_3)$ of Proposition 4.8, without further assumptions on the elliptic curves.

Proposition 5.1

Let A and B be abelian surfaces and $\Phi : {\mathbf {D}}(B) \rightarrow {\mathbf {D}}(A)$ be an equivalence of derived categories. Fix two distinct primes $p_1$ and $p_2$. Then there exists an equivalence $\Psi : {\mathbf {D}}(B) \rightarrow {\mathbf {D}}(C)$ with $C\in \{A,\, {\widehat{A}}\}$ such that the vector

$$\begin{aligned} (r, \, l, \, \chi ) := \Psi ^{\mathrm{CH}}(0, \,0, \,1) \end{aligned}$$

satisfies one the two following statements:

• (i) r is relatively prime with both $p_1$ and $p_2$;

• (ii) either $p_1$ divides r but not $\chi$ and $p_2$ divides $\chi$ but not r, or vice versa.

Proof

Set

$$\begin{aligned}&v_0 := (r_0, \, l_0, \, \chi _0) = \Phi ^{\mathrm{CH}}(0, \,0, \,1)\\&w_0 := (s_0, \, h_0, \, \xi _0) = \Phi ^{\mathrm{CH}}(1, \,0, \,0). \end{aligned}$$

Since $\Phi$ is an equivalence, by (2.2) we have that

$$\begin{aligned} 1 = \langle v_0, w_0\rangle _A = I - s_0 \, \chi _0 - r_0 \, \xi _0,\quad \hbox { where }\quad I := l_0\cdot h_0. \end{aligned}$$

(5.1)

Let $H_0$ be a line bundle on A such that its class in the Néron–Severi group is $h_0$. Therefore at the level of numerical Chow rings the equivalence $\Phi _n := T_A(H_0^{\otimes n}) \circ \Phi : {\mathbf {D}}(B) \rightarrow {\mathbf {D}}(A)$ ($n\in {\mathbf {Z}}_{>0}$) sends (0, 0, 1) to

$$\begin{aligned} v_n \, := \, \Phi _n^{\mathrm{CH}}(0,0,1) = \big (r_0,\, l_0\,+\,r_0\,n\,h_0, \,\chi _n \big ) \end{aligned}$$

where

$$\begin{aligned} \chi _n\, := \, \chi _0 + n\,I+ r_0 \, n^2 \,\frac{h_0^2}{2}. \end{aligned}$$

(5.2)

We divide the proof in five cases.

Case I Suppose that neither $p_1$ nor $p_2$ divides $\chi _0$. In this case the equivalence $\Psi$ is given by the composition ${{\mathcal {S}}}_A \circ \Phi \, : \, {\mathbf {D}}(B)\rightarrow {\mathbf {D}}({\widehat{A}})$.

Case II Suppose that both $p_1$ and $p_2$ divide both $r_0$ and $\chi _0$. By (5.1) we see that I is relatively prime with $p_1$ and $p_2$ as well. Now choose a positive integer n coprime with both $p_1$ and $p_2$. Therefore by looking at the definition (5.2) of $\chi _n$, this immediately implies that $\chi _n$ is relatively prime to both $p_1$ and $p_2$. We conclude then as in Case I.

Case III Suppose that both $p_1$ and $p_2$ divide $r_0$, and that precisely one of them, say $p_1$, divides $\chi _0$. We choose a positive integer n such that n is relatively prime to both $p_1$ and $p_2$. By (5.1) I is relatively prime to $p_1$, and by (5.2) $p_1$ does not divide $\chi _n$. Moreover, again by (5.2) and the fact that n is general, we can suppose that $p_2$ does not divide $\chi _n$ as well. We then set $\Psi := {{\mathcal {S}}}_A \circ \Phi _n$.

Case IV Suppose that both $p_1$ and $p_2$ divide $\chi _0$ and that precisely one of them, say $p_1$, divides $r_0$. In this case we proceed as in Case III by considering the composition ${{\mathcal {S}}}_A\circ \Phi$ in place of $\Phi$.

Case V Suppose that one of the primes, say $p_1$, divides both $r_0$ and $\chi _0$, but $p_2$ divides neither $r_0$ nor $\chi _0$. Let $n=p_2$ and consider $\Phi _n$. By (5.1) $p_1$ does not divide I, and hence $p_1$ does not divide $\chi _n$. Moreover, by our choice of n, we have that $p_2$ does not divide $\chi _n$ as well. We then conclude as in Case I. $\square$

Proposition 5.2

Assume the hypotheses of Setting 4.5 and let $\Phi : {\mathbf {D}}(B)\rightarrow {\mathbf {D}}(A)$ be an equivalence of triangulated categories. Moreover assume that $\mathrm{deg}\,\nu \ge 2$. Then there exists an equivalence $\Xi : {\mathbf {D}}(B) \rightarrow {\mathbf {D}}(C)$ with $C\in \{A, \, {\widehat{A}}\}$ such that the vector

$$\begin{aligned} (r, \, l, \, \chi ) := \Xi ^{\mathrm{CH}}(0,\,0,\,1) \end{aligned}$$

satisfies the following conditions:

• (i) r is positive and relatively prime with p;

• (ii) the class $l \in \mathrm{CH}^1(C)$ is ample;

• (iii) $\chi$ is relatively prime with r.

Now set $\lambda =\nu$ if $C=A$ and $\lambda ={{\widehat{\mu }}}$ otherwise. Then the class l is the pull-back of some ample class in $\mathrm{CH}^1(E\times F)$ via $\lambda$.

Proof

By using Proposition 5.1 with $p_1=p$ and $p_2=\deg \, \nu$, we can find an equivalence $\Psi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(C)$ with $C\in \{A,{\widehat{A}}\}$ such that the vector

$$\begin{aligned} v_0:=(r_0, \, l_0, \, \chi _0)=\Psi ^{\mathrm{CH}}(0, \,0, \,1) \end{aligned}$$

satisfies one of the two following conditions: (a) $r_0$ is relatively prime to both $p_1$ and $p_2$, or (b) one of the primes $p_1$ and $p_2$ divides $r_0$ but not $\chi _0$, while the other divides $\chi _0$ but not $r_0$. Set $\lambda =\nu$ if $C=A$ and $\lambda ={\widehat{\mu }}$ otherwise. We claim that there exists an equivalence $\Xi _1:{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(C)$ such that in the vector

$$\begin{aligned} v_1:=(r_1, \, \lambda ^*l_1, \, \chi _1) = \Xi _1^{\mathrm{CH}}(0, \, 0, \,1), \end{aligned}$$

$r_1$ is positive and relatively prime with p, and $l_1\in \mathrm{CH}^1(E\times F)$. In order to prove the claim, we distinguish the two cases (a) and (b) mentioned above. First consider case (a). As $r_0$ is not zero, we can make it positive by composing with the shift functor, if necessary. Let L be a line bundle representing $l_0$ and m be a positive integer such that $p_2^2$ divides $(r_0 \, m+1)$. Hence we can write $1+r_0 \, m= p_2^2 \, u$ for some integer u and we consider the composition $T_C(L^{\otimes m})\circ \Psi$. Then

$$\begin{aligned} \big (T_C(L^{\otimes m})\circ \Psi \big )^{\mathrm{CH}}(0,0,1) = \big (r_0, \, (p_2^2 \, u)\, l_0, \,\chi _1\big ) \end{aligned}$$

for some integer $\chi _1$. By Proposition 2.3 there exists a class $l_1\in \mathrm{CH}^1(E\times F)$ such that $(p_2^2 \, u) \, l_0=\lambda ^* (u\, l_1)$. This proves the claim in case (a) as we can set $\Xi _1:=T_C(L^{\otimes m})\circ \Psi$ and $v_1:=(r_0, \, (p_2^2 \,u)\, l_0, \,\chi _1)$.

Now consider case (b). If necessary we replace $\Psi$ with ${{\mathcal {S}}}_C\circ \Psi$ in order to make $r_0$ divisible by $p_1=p$ but relatively prime with $p_2=\mathrm{deg} \, \nu$. Let L and m be as above. Then the equivalence $\Psi _1 := T_C(L^{\otimes m})\circ \Psi$ sends the vector (0, 0, 1) to

$$\begin{aligned} \Psi _1^{\mathrm{CH}}(0, \, 0, \, 1) = \left( r_0, \, p_2^2\, u\, l_0, \, \chi _0 \, +\, m\, l_0^2\, +\, r_0\, m^2 \frac{l_0^2}{2}\right) \, := \, (r_0, \, p_2^2 \, l_2, \, \chi _2) \end{aligned}$$

where $l_2$ is a class in $\mathrm{CH}^1(C)$. Since $\langle v_0,v_0 \rangle _C=0$, we have that $l_0^2=2r_0\chi _0$ and hence

$$\begin{aligned} \chi _2 = \chi _0 \, +\,2 \, m \, r_0\, \chi _0 \, +\, m^2\, r_0^2 \, \chi _0. \end{aligned}$$

As $p_1$ divides $r_0$ but does not divide $\chi _0$, it follows that

$$\begin{aligned} \chi _2 \; \equiv \; \chi _0 \; \not \equiv \; 0\pmod p. \end{aligned}$$

Hence,

$$\begin{aligned} \big ({{\mathcal {S}}}_C \circ \Psi _1\big )^{\mathrm{CH}}(0,0,1) = \big (\chi _2, \,p_2^2 \, \omega , \, r_0) = (\chi _2, \, \lambda ^*\omega ', \,r_0\big ) \end{aligned}$$

for some elements $\omega \in \mathrm{CH}^1(C)$ and $\omega '\in \mathrm{CH}^1(E\times F)$. Also, $p_2=\mathrm{deg}\, \nu$ does not divide $r_0$ (here we use the fact that ${{\mathcal {S}}}_{C}^{\mathrm{CH}}$ induces an homomorphism $\mathrm{CH}^1(C)\rightarrow \mathrm{CH}^1({\widehat{C}})$; see Sect. 2.2). If necessary we can make the integer $\chi _2$ positive by composing with the shift functor. This concludes the proof of the claim.

Now let $w=(s, \, h, \,\xi )$ be the Mukai vector of $\Xi _1^\mathrm{CH}(1,0,0)$ so that $\langle w, v_1\rangle _C=1$. Moreover let H be a line bundle whose numerical class is h and note that

$$\begin{aligned} I- r_1 \, \xi \, - \chi _1 \, s = 1\quad \hbox { where } \quad I:=l_1\cdot h. \end{aligned}$$

(5.3)

Choose a positive integer n such that

$$\begin{aligned} n \, p_2^2 \,I + \chi _1\; \not \equiv 0 \pmod q \quad \hbox { for every prime divisor }q\ne p_2 \hbox { of }r_1 \hbox { that does not divide }I. \end{aligned}$$

Now set $\Xi _2:=T_C(H^{\otimes (n \,p_2^2)})\circ \Xi _1$ and $(r_2,l_2,\chi _2):=\Xi _2^{\mathrm{CH}}(0,0,1)$. With a simple calculation we find

$$\begin{aligned} r_2 = r_1, \quad l_2 = \lambda ^* l_1 + r_1 \, n \, p_2^2 \, h,\quad \chi _2 = \chi _1 + n \, p_2^2 \, I +r_1 \, n^2 \, p_2^4 \, \frac{h^2}{2}. \end{aligned}$$

(5.4)

We note that $r_2$ is not divisible by p, and moreover that by (5.4), $\chi _2$ is not divisible by any prime divisor $q\ne p_2$ of $r_1$ that does not divide I. On the other hand, if a prime divisor $q\ne p_2$ divides both $r_1$ and I, then by (5.3) it does not divide $\chi _1$, and hence does not divide $\chi _2$. Finally we prove that $\chi _2$ is not divisible by $p_2$ in the case where $p_2$ divides $r_1$. But this follows by the construction of $\Xi _1$, and by noting that in the case (b) discussed earlier, $p_2$ does not divide $r_0$.

Now consider the composition $\Xi _3 \, := \, T_C(\lambda ^*\Theta ^{\otimes (r_2 \,d)})\circ \Xi _2$ where $\Theta :={{\mathcal {O}}}_E(O_E)\boxtimes {{\mathcal {O}}}_F(O_F)$ and $d\gg 0$ is a positive integer. By a direct computation we have that $\Xi _3^{\mathrm{CH}}$ sends the vector (0, 0, 1) to

$$\begin{aligned} v_3 := (r_2, \, l_2 + r_2^2 \, d\, \lambda ^*\theta ,\, \chi _3) \end{aligned}$$

where $\theta$ is the numerical class of $\Theta$ and

$$\begin{aligned} \chi _3 := \chi _2 \, +\, r_2\, d \,(l_2 \cdot \lambda ^*\theta )+ r_2^3 \,d^2 \, \frac{(\lambda ^*\theta )^2}{2}. \end{aligned}$$

By Proposition 2.3 and (5.4) we can write $l_2=\lambda ^*l_3$ for some class $l_3\in \mathrm{CH}^1(E\times F)$, and hence

$$\begin{aligned} \chi _3 \, \equiv \, \chi _2 + r_2 \, d \, p_2^c\, (l_3\cdot \theta ) + r_2^3 \, p_2^c\, d^2\,\frac{\theta ^2}{2} \, \equiv \, \chi _2 \pmod {p_2} \end{aligned}$$

as the isogeny $\lambda$ has degree either $p_2^c$ with $c=1$ if $C=A$, and $c=3$ otherwise. Therefore the first component of $v_3$ is still positive and relatively prime with p, while the second component is a pull-back of an ample class in $\mathrm{CH}^1(E\times F)$ (for $d\gg 0$). Moreover $\chi _3 \, \equiv \, \chi _2 \,(\hbox {mod }\,r_2)$ and hence it is still relatively prime with $r_2=r_1$. Our desired equivalence is hence given by $\Xi :=\Xi _3$. $\square$

Now we consider separately the case of supersingular abelian surfaces and the case of abelian surfaces that are not supersingular.

5.1 The case where one of the two curves is ordinary

The above results imply that when one of the elliptic curve involved is not supersingular then we can construct an equivalence satisfying $(E_1)$, $(E_2)$ and $(E_3)$. In order to conclude we need to prove that the hypotheses $(A_1)$ and $(A_2)$ of Proposition 4.8 hold as well. We will first prove a couple of auxiliary results.

Proposition 5.3

Let E and F be ordinary elliptic curves. Then there exist projective liftings ${{\mathcal {E}}}\rightarrow W$ and ${{\mathcal {F}}}\rightarrow W$ of E and F over the ring of Witt vectors, respectively, such that the restriction morphism $\mathrm{Pic}({{\mathcal {E}}}\times _W{{\mathcal {F}}}) \rightarrow \mathrm{Pic}(E\times F)$ is surjective.

Proof

The product $E\times F$ is an ordinary abelian surface so it has a canonical lift $({{\mathcal {Y}}}\rightarrow W, F_{{{\mathcal {Y}}}})$ by virtue of Theorem 2.8. Moreover the restriction morphism $\mathrm{Pic}({{\mathcal {Y}}})\rightarrow \mathrm{Pic}(E\times F)$ is surjective. However by using the universal property of the fiber product, it is immediate to show that ${{\mathcal {Y}}}\simeq {{\mathcal {E}}}\times _W{{\mathcal {F}}}$ where ${{\mathcal {E}}}\rightarrow W$ and ${{\mathcal {F}}}\rightarrow W$ are the canonical lifts of E and F respectively. $\square$

Proposition 5.4

If E is an ordinary elliptic curve and F is supersingular, then for any projective lifts ${{\mathcal {E}}}\rightarrow W$ and ${{\mathcal {F}}}\rightarrow W$ of E and F respectively, the restriction morphism $\mathrm{Pic}({{\mathcal {E}}}\times _W {{\mathcal {F}}})\rightarrow \mathrm{Pic}(E\times F)$ is surjective.

Proof

As $\mathrm{Hom}(E,F)=0$ we obtain an isomorphism $\mathrm{Pic}(E\times F)\simeq \mathrm{Pic}(E)\times \mathrm{Pic}(F)$. Let now $\mathrm{pr}_E^*L_E\otimes \mathrm{pr}_F^*L_F$ be an arbitrary line bundle on $E\times F$. Since line bundles on curves lift, we can consider lifts ${\mathcal {L}}_{{{\mathcal {E}}}}$ and ${\mathcal {L}}_{{{\mathcal {F}}}}$ of $L_E$ and $L_F$ respectively. Hence the line bundle $\mathrm{pr}_{{{\mathcal {E}}}}^*{\mathcal {L}}_{{{\mathcal {E}}}}\otimes \mathrm{pr}_{{{\mathcal {F}}}}^*{\mathcal {L}}_{{{\mathcal {F}}}}$ on ${{\mathcal {E}}}\times _W{{\mathcal {F}}}$ is a lift of $\mathrm{pr}_E^*L_E\otimes \mathrm{pr}_F^*L_F$. $\square$

Proposition 5.5

Assume the hypotheses of Setting 4.5 and let $\Phi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(A)$ be an equivalence of derived categories of abelian surfaces. If both E and F are ordinary elliptic curves, then the hypotheses of Proposition 4.8 hold.

Proof

By Propositions 3.2 and 5.2 there exists an equivalence $\Xi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(C)$ with $C\in \{A,{\widehat{A}}\}$ such that the vector $\Xi ^\mathrm{CH}(0,0,1)=(r,\lambda ^*l,\chi )$ satisfies the hypotheses $(E_1)$, $(E_2)$ and $(E_3)$ of Proposition 4.8. Let L be a line bundle on $E\times F$ with class $l\in \mathrm{CH}^1(E\times F)$. By Proposition 5.3 there exist projective lifts ${{\mathcal {E}}}\rightarrow W$ and ${{\mathcal {F}}}\rightarrow W$ of E and F to the ring of Witt vectors W, and a lift ${\mathcal {L}}\in \mathrm{Pic}({{\mathcal {E}}}\times _W{{\mathcal {F}}})$ of L. Let $\lambda _W:{\mathcal {C}}\rightarrow {{\mathcal {E}}}\times _W{{\mathcal {F}}}$ be the lift of $\lambda :C\rightarrow E\times F$ defined by Proposition 4.7. It follows that $\lambda _W^*{\mathcal {L}}$ lifts $\lambda ^*L$ which proves condition $(A_1)$. In order to prove $(A_2)$ we can assume that F has an automorphism of order three. Then by Theorem 2.8 the geometric generic fiber ${{\mathcal {F}}}_{\eta }$ admits an automorphism of order three and hence $\mathrm{rk \, CH}^1 ({{\mathcal {E}}}_{\eta }\times {{\mathcal {F}}}_{\eta })\in \{2,4\}$ where ${{\mathcal {E}}}_{\eta }$ is the geometric generic fiber of the lift ${{\mathcal {E}}}\rightarrow W$. $\square$

Proposition 5.6

Assume the hypotheses of Setting 4.5 and let $\Phi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(A)$ be an equivalence of derived categories of abelian surfaces. If E is ordinary and F is supersingular or vice versa, then the hypotheses of Proposition 4.8 hold.

Proof

By Propositions 3.2 and 5.2 there exists an equivalence $\Xi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(C)$ with $C\in \{A,{\widehat{A}}\}$ such that the vector $\Xi ^\mathrm{CH}(0,0,1)=(r,\lambda ^*l,\chi )$ satisfies the hypotheses $(E_1)$, $(E_2)$ and $(E_3)$ of Proposition 4.8. By Proposition 5.4 we can choose general lifts ${{\mathcal {E}}}$ and ${{\mathcal {F}}}$ of E and F to W respectively and a line bundle ${\mathcal {L}}\in \mathrm{Pic}({\mathcal {C}})$ such that the condition $(A_1)$ holds (see the argument of Proposition 5.5). Furthermore, since any fixed elliptic curve has a 1-dimensional family of deformations and for any choice of ${{\mathcal {E}}}$, there are only finitely many elliptic curves isogenous to ${{\mathcal {E}}}_{\eta }$, we may choose ${{\mathcal {E}}}$ and ${{\mathcal {F}}}$ so that there are no non-trivial morphisms between the geometric generic fibers ${{\mathcal {E}}}_{\eta }$ and ${{\mathcal {F}}}_{\eta }$. It follows that $\mathrm{rk \, NS}({{\mathcal {E}}}_{\eta }\times {{\mathcal {F}}}_{\eta })=2$ independently of whether F admits an automorphism group of order three or not. As in Proposition 5.5 this immediately implies that $\mathrm{rk \, NS}({{\mathcal {C}}}_{\eta })=2$. $\square$

5.2 Supersingular case

We are going to prove that the hypotheses of Proposition 4.8 hold when the elliptic curves E and F are both supersingular. The following proposition proves the conditions $(E_1)$, $(E_2)$ and $(E_3)$.

Proposition 5.7

Assume the hypotheses of Setting 4.5 with $\mathrm{deg}\,\nu \ge 2$ and assume that the elliptic curves E and F are supersingular. Moreover let $\Phi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(A)$ be an equivalence of derived categories of abelian surfaces. Then there exists an equivalence $\Xi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(C)$ with $C\in \{A,{\widehat{A}}\}$ such that the Mukai vector

$$\begin{aligned} (r, \, l, \, \chi ) := \Xi ^{\mathrm{CH}}(0, \,0, \,1) \end{aligned}$$

satisfies the following conditions:

• (i) r is positive and relatively prime with p;

• (ii) the class $l\in NS(C)$ is ample;

• (iii) $\chi$ is relatively prime with r.

Now set $\lambda =\nu$ if $C=A$, and $\lambda ={{\widehat{\mu }}}$ otherwise. Then $l=\lambda ^*l'$ where $l'=l(\varphi ,d_1,d_2)$ is the class of a line bundle on $E\times F$ with $\varphi$ an étale isogeny.

Proof

Proceeding as in the proof of Proposition 5.2, we can construct an equivalence $\Psi _1 : {\mathbf {D}}(B) \rightarrow {\mathbf {D}}(C)$ where $C\in \{A,{\widehat{A}}\}$ such that in the vector

$$\begin{aligned} v_1 := (r_1, \, \lambda ^*l_1,\, \chi _1) = \Psi _1^\mathrm{CH}(0,0,1), \end{aligned}$$

$r_1$ is relatively prime with p, and $l_1=l(\varphi ,m_1,m_2)$ is the class of a line bundle on $E\times F$ for some morphism $\varphi :F\rightarrow E$ and integers $m_1,m_2$ (see Proposition 2.7). We notice that we can assume $r_1$ positive by eventually composing with the shift functor. First, suppose that $\varphi$ is either the constant morphism or non-separable. Let $t\ne p$ be a prime and let $\xi :F\rightarrow E$ be a separable isogeny of degree $t^k$ ($k\in {\mathbf {Z}}_{>0}$) determined by Proposition 2.4. Now consider the composition of equivalences $\Psi _2:=T_C\big (\lambda ^*(1_E\times \xi )^*{{\mathcal {M}}}_E\big ) \circ \Psi _1:{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(C)$. As the class of $(1_E\times \xi )^*{{\mathcal {M}}}_E$ is $l(\xi ,0,0)$, by Corollary 2.6 we have that $\Psi _2^{\mathrm{CH}}$ sends the vector (0, 0, 1) to

$$\begin{aligned} v_2 := \big (r_1, \, \lambda ^*l(\varphi \, +\, r_1 \, \xi ,\, m_1, \, m_2), \, \chi _2\big ) \end{aligned}$$

for some integer $\chi _2$. Recall that if $f_1$ and $f_2$ are two isogenies of elliptic curves with $f_1$ inseparable, then $f_1+f_2$ is separable if and only if $f_2$ is separable. Then as $r_1$ is relatively prime with p, the isogeny $\gamma :=\varphi +r_2 \, \xi$ is separable (indeed the composition of separable isogenies is separable, and the multiplication-by-n map is separable if and only if n is coprime with p), and hence étale.

Let $w:=(s, h,\zeta )=\Psi _2^{\mathrm{CH}}(1,0,0)$ and note that $\langle v_2, w\rangle _C=1$. By Proposition 2.3 the class $p_2^2 \, h$ (where $p_2=\mathrm{deg}\nu$) is in the image of the pull-back $\lambda ^*:\mathrm{CH}^1(E\times F)\rightarrow \mathrm{CH}^1(C)$. Therefore we can write

$$\begin{aligned} p_2^2 \, h = \lambda ^*l(\psi ,\, k_1, \, k_2) \end{aligned}$$

for some morphism $\psi$ and integers $k_1,k_2$. Consider the equivalence $\Psi _3 := T_C(H^{\otimes (n \, p\, p_2^2)})\circ \Psi _2$ which sends the vector (0, 0, 1) to

$$\begin{aligned}&v_3 := \Big (r_1, \, \lambda ^*l \big (\gamma \, +\, r_1 \, p\, n\, \psi , \, m_1 \, +\, r_1 \, p\, n\, k_1, \, m_2\, +\, r_1\, p\, n\, k_2 \big ), \\&\quad \quad \quad \ \chi _2 \, +\, p\, p_2^2 \, n\, I + r_1\, p^2 \, p_2^4\, n^2\, \frac{h^2}{2}\Big ) \end{aligned}$$

where

$$\begin{aligned} I\; := \, \lambda ^*(\gamma ,\, m_1,\, m_2) \cdot h. \end{aligned}$$

As $(r_1 \, p\, n)\psi$ is either the zero morphism or non-separable, we have that $\gamma + (r_1 \, p \, n\, )\psi$ is a separable isogeny. Now choose a positive integer n so that

$$\begin{aligned} p \, p_2^2 \, n\, I\, +\, \chi _2 \; \not \equiv \; 0 \pmod {q} \quad \quad \hbox {for every prime divisor } q\ne p_2\hbox { of }r_2\hbox { that does not divide }I. \end{aligned}$$

By the same argument as Proposition 5.2, this choice of n ensures that the third component of $v_3$ is relatively prime with $r_1$.

Now we define the line bundle $\Theta :={{\mathcal {O}}}_E(O_E)\boxtimes {{\mathcal {O}}}_F(O_F)$ on $E\times F$ and we consider the equivalence $T_C(\lambda ^*\Theta ^{\otimes (r_1 \, d)})\circ \Psi _3$ with $d\gg 0$ a positive integer. Take $\theta :=l(0_E,1,1)$ to be the class of $\Theta$. The equivalence $T_C(\lambda ^*\Theta ^{\otimes (r_1 \, d)})\circ \Psi _3$ sends (0, 0, 1) to

$$\begin{aligned} v_4 = \Big (r_1, \, \lambda ^*(\gamma \, +\, r_1\, n \, p \, \psi ,m_1 \, +\, r_1\, p\, n\, k_1\, +\, r_1^2\, d, \, m_2\, +\, r_2 \, p\, n\, k_2 \, +\, r_1^2 \,d), \chi _4\Big ) \end{aligned}$$

where

$$\begin{aligned} \chi _4:= & {} \chi _2 \, +\, p\, p_2^2 \, n\, I + r_1 \, p^2 \, p_2^4 \, n^2\, \frac{h^2}{2} \, \\&+\, r_1 \, d \big (\theta \cdot \lambda ^*l(\gamma \, +\, r_1 \, p\, n \, \psi , m_1 \, +\, r_1 \, p\, n\, k_1, m_2 \, +\, r_1\, p\, n\, k_2)\big ) \, +\, r_1^3 \, d^2 \, \frac{\theta ^2}{2}. \end{aligned}$$

As $\chi _4$ is congruent to the third component of $v_3$ modulo $r_1$, we have that $\chi _4$ is still relatively prime with $r_1$. Moreover, for d sufficiently large the second component of $v_4$ is ample. Finally, $r_1$ is relatively prime with p, and hence $T_C(\lambda ^*\Theta ^{\otimes (r_1 \,d)})\circ \Psi _3$ is the equivalence we are looking for.

To conclude the proof we need to analyze the case when $\varphi$ is separable. But in this case the proof is simpler as there is no need to introduce the isogeny $\xi$ and the equivalence $\Psi _2$. Then it is enough to set $\gamma =\varphi$ and proceed as in the inseparable case. $\square$

Proposition 5.8

Assume the hypotheses of Setting 4.5 and let $\Phi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(A)$ be an equivalence of derived categories of abelian surfaces. Moreover assume that the elliptic curves E and F are both supersingular. Then the hypotheses of Proposition 4.8 hold.

Proof

By Propositions 3.2 and 5.7 we can find an equivalence $\Xi :{\mathbf {D}}(B)\rightarrow {\mathbf {D}}(C)$ with $C\in \{A,{\widehat{A}}\}$ such that the vector

$$\begin{aligned} v := \big (r, \, \lambda ^*l(\varphi , m_1,m_2), \, \chi \big ) = \Xi ^{\mathrm{CH}}(0, \,0, \,1) \end{aligned}$$

satisfies the assumptions $(E_1)$, $(E_2)$, and $(E_3)$ of Proposition 4.8. The class $l(\varphi ,m_1,m_2)$ is the class of an ample line bundle $L(\varphi ,M_1,M_2)$ on $E\times F$ where $M_1$ and $M_2$ are line bundles on E and F respectively, and $\varphi : F\rightarrow E$ is the constant morphism $O_E$ in the case where $\nu$ is an isomorphism, or an étale isogeny otherwise. Let ${{\mathcal {E}}}\rightarrow W$ be a lift of E to the ring of Witt vectors. If $\varphi =O_E$ is the constant morphism, then on any lift ${{\mathcal {F}}}\rightarrow W$ of F we can construct a lift of $L=M_1\boxtimes M_2$ by simply lifting $M_1$ and $M_2$ to W and taking their exterior product. Now assume that $\varphi$ is a separable isogeny. Then Theorem 2.9 determines a projective lift ${{\mathcal {F}}}\rightarrow W$ of ${{\mathcal {F}}}$ and an étale cover ${\widetilde{\varphi }}:{{\mathcal {F}}}\rightarrow {{\mathcal {E}}}$ that specializes to $\varphi$. It is not difficult to check that $L(\varphi ,M_1,M_2)$ lifts to a line bundle ${\mathcal {L}}$ on ${{\mathcal {E}}}\times _W{{\mathcal {F}}}$. This goes as follows. As line bundles on curves lift, we can find a lift of ${{\mathcal {O}}}_E(O_E)$ which in turn allows us to construct a lift ${{\mathcal {M}}}_{E,W}$ to W of the Mumford line bundle ${{\mathcal {M}}}_E$ (cf. Sect. 2.4). Denote by $M_{1,W}$ and $M_{2,W}$ the liftings of $M_1$ and $M_2$ on ${{\mathcal {E}}}$ and ${{\mathcal {F}}}$ respectively. The line bundle ${\mathcal {L}}:=(1_{{{\mathcal {E}}}} \times _W {\widetilde{\varphi }})^*{{\mathcal {M}}}_{E,W} \otimes \mathrm{pr}_{{{\mathcal {E}}}}^*M_{1,W}\otimes \mathrm{pr}_{{{\mathcal {F}}}}^*M_{2,W}$ is a lift of $L(\varphi ,M_1,M_2)$, where $\mathrm{pr}_{{{\mathcal {E}}}}$ and $\mathrm{pr}_{{{\mathcal {F}}}}$ are the obvious projections. In conclusion the line bundle $\lambda _W^*{{\mathcal {L}}}$ lifts $\lambda ^*L(\varphi ,M_1,M_2)$ where $\lambda _W:{\mathcal {C}}\rightarrow {{\mathcal {E}}}\times _W{{\mathcal {F}}}$ is the lift from Proposition 4.8. This proves the condition $(A_1)$ in the case $\mathrm{deg}\,\nu =1,2$.

Now suppose $\mathrm{deg}\,\nu =3$ and that F has an automorphism $\rho :F\rightarrow F$ of order three. By a result of Deuring (cf. [29, p. 189 or p. 172]) it is possible to lift a supersingular elliptic curve together with an endomorphism over a finite ramified extension W of the ring of Witt vectors. Thus we have lifts ${{\mathcal {F}}}_0\rightarrow W$ and $\rho _W:{{\mathcal {F}}}_0\rightarrow {{\mathcal {F}}}_0$ of F and $\rho$ to W. The étale cover ${\widehat{\varphi }}:E\rightarrow F$ determines a lift ${{\mathcal {E}}}_0$ of E together with a lift ${\widetilde{\varphi }}_0$ of ${\widehat{\varphi }}$ over W. Now, denote by $\lambda _{W,0}:{\mathcal {C}}_0\rightarrow {{\mathcal {E}}}_0\times _W{{\mathcal {F}}}_0$ the lift of $\lambda$ as defined in Proposition 4.8. After noting that there is an isomorphism $(1_E\times \varphi )^*{{\mathcal {M}}}_E\simeq ({\widehat{\varphi }}\times 1_F)^*{{\mathcal {M}}}_F$, and hence that

$$\begin{aligned} L(\varphi ,M_1,M_2)\simeq ({\widehat{\varphi }}\times 1_F)^*{{\mathcal {M}}}_F\otimes \mathrm{pr}_{E}^*M_1\otimes \mathrm{pr}_F^*M_2, \end{aligned}$$

the previous argument shows that the line bundle $\lambda ^*L(\varphi ,M_1,M_2)$ lifts to ${\mathcal {C}}_0$. Moreover the restriction of $\rho _W$ to the geometric generic fiber $({{\mathcal {F}}}_0)_{\eta }$ is an automorphism that is not proportional to the identity. Hence $\mathrm{rk \,CH}^1\big (({{\mathcal {E}}}_0)_{\eta }\times ({{\mathcal {F}}}_0)_{\eta } \big )$ is either 2 or 4 according to whether or not there is an isogeny between $({{\mathcal {E}}}_0)_{\eta }$ and $({{\mathcal {F}}}_0)_{\eta }$. As the rank of the Néron–Severi group does not change under separable isogenies, we have that $\mathrm{rk \, CH}^1(({{\mathcal {C}}}_0)_{\eta })\in \{2,4\}$ where $({{\mathcal {C}}}_0)_{\eta }$ is the geometric generic fiber of ${{\mathcal {C}}}_0$. In particular the assumption $(A_2)$ holds. $\square$

6 Canonical covers of Enriques surfaces

An Enriques surfaceS over an algebraically closed field k of characteristic $p\ne 2$ is a smooth projective minimal surface with canonical bundle $\omega _S$ of order two, $\chi ({{\mathcal {O}}}_S)=1$, and $b_2(S)=10$. The canonical cover $\pi :X\rightarrow S$ induced by $\omega _S$ is a double étale cover with X a K3 surface. Let $\Phi :{\mathbf {D}}(Y)\rightarrow {\mathbf {D}}(X)$ be a derived equivalence so that Y is itself a K3 surface by [17, Proposition 3.9]. We aim to prove Theorem 1.3, namely that $X\simeq Y$.

In [17] the authors prove that Shioda-supersingular K3 surfaces do not admit any non-trivial Fourier–Mukai partners, thus we can assume that X has Picard rank less than 22. Since in odd characteristic Shioda-supersingularity is equivalent to Artin-supersingularity (cf. for instance [30]), we can assume that the formal Brauer group of X is of finite height. In particular there exists a lift ${\mathcal {X}}\rightarrow W$ of X over the ring of Witt vectors such that $\mathrm{NS}(X)\simeq \mathrm{NS}({\mathcal {X}}_\eta )$, where as usual ${\mathcal {X}}_\eta$ is the geometric generic fiber [28, p. 505]. By the work of Jang [12, Theorem 2.5] there is a primitive embedding of the Enriques lattice $\Gamma (2):=U(2)\oplus E_8(-2)$ of S into $\mathrm{NS}(X)$ such that the orthogonal complement of the embedding does not contain any vector of self intersection $-2$. Using the isomorphism $\mathrm{NS}(X)\simeq \mathrm{NS}({\mathcal {X}}_\eta )$, together with the characterization of Enriques-K3 surfaces in terms of its periods [27, Theorem 1.14], we deduce that ${\mathcal {X}}_\eta$ is a K3 surface arising as the canonical cover of an Enriques surface. In particular ${\mathcal {X}}_\eta$ does not have any non-trivial Fourier–Mukai partner thanks to [34, Theorem 1.1]. On the other hand, [17, Proposition 8.2] implies that Y is isomorphic to a moduli space ${\mathcal {M}}_h(v)$ of h-Gieseker-stable sheaves for some Mukai vector $v=(r, l, \chi )$. Since all the line bundles on X deform to line bundles over ${\mathcal {X}}\rightarrow W$, we can consider the relative moduli space ${{\mathcal {M}}}_{{\mathcal {X}}/W}(r, {\widetilde{l}}, \chi )\rightarrow W$ where ${\widetilde{l}}$ is a lift of l. The geometric generic fiber of ${\mathcal {M}}_{{\mathcal {X}}/W}(r, {\widetilde{l}}, \chi )\rightarrow W$ is by construction a Fourier–Mukai partner of ${\mathcal {X}}_\eta$ and therefore, by the previous considerations, it is isomorphic to ${\mathcal {X}}_\eta$. We conclude by using [17, Lemma 6.5], which says that the isomorphism between the geometric generic fibers of relative K3 surfaces induces an isomorphism between the closed fibers.