Class \(\mathcal {B}\) or not class \(\mathcal {B}\), that is the question—Whether ’tis nobler in the mind to suffer The tracts that lie over unbounded values, Or to take arms against these spots of trouble, And by assumption, ban them? (loosely based on) Hamlet
Abstract
Hyperbolicity plays an important role in the study of dynamical systems, and is a key concept in the iteration of rational functions of one complex variable. Hyperbolic systems have also been considered in the study of transcendental entire functions. There does not appear to be an agreed definition of the concept in this context, due to complications arising from the non-compactness of the phase space. In this article, we consider a natural definition of hyperbolicity that requires expanding properties on the preimage of a punctured neighbourhood of the isolated singularity. We show that this definition is equivalent to another commonly used one: a transcendental entire function is hyperbolic if and only if its postsingular set is a compact subset of the Fatou set. This leads us to propose that this notion should be used as the general definition of hyperbolicity in the context of entire functions, and, in particular, that speaking about hyperbolicity makes sense only within the Eremenko–Lyubich class \(\mathcal {B}\) of transcendental entire functions with a bounded set of singular values. We also considerably strengthen a recent characterisation of the class \(\mathcal {B}\), by showing that functions outside of this class cannot be expanding with respect to a metric whose density decays at most polynomially. In particular, this implies that no transcendental entire function can be expanding with respect to the spherical metric. Finally we give a characterisation of an analogous class of functions analytic in a hyperbolic domain.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is a general principle in the investigation of dynamical systems that hyperbolic systems (also known as “Axiom A”, following Smale [27]) are the first class to investigate in a given setting: they exhibit the simplest behaviour, yet their study frequently leads to a better understanding of more complicated systems.
In this article, we consider (non-invertible) dynamics in one complex variable. For rational maps, hyperbolic behaviour was understood, at least in rather general terms, already by Fatou [15, pp. 72–73], though, of course, he did not use this terminology.
More precisely, a rational map \(f:\hat{\mathbb {C}}\rightarrow \hat{\mathbb {C}}\) is said to be hyperbolic if one of the following, equivalent, conditions holds [3, Section 9.7] (see below for definitions):
-
(a)
the function f is expanding with respect to a suitable conformal metric defined on a neighbourhood of its Julia set;
-
(b)
every critical value of f belongs to the basin of an attracting periodic cycle;
-
(c)
the postsingular set is a subset of the Fatou set.
Moreover [23, Theorem 4.4] every hyperbolic rational map satisfies
-
(d)
f is stable; in other words, any nearby rational map is topologically conjugate to f on its Julia set, with the conjugacy depending continuously on the perturbation.
The famous Hyperbolicity Conjecture asserts that condition (d) is also equivalent to hyperbolicity; this question essentially goes back to Fatou. See the final sentence of Chapitre IV in [15, p. 73], and also compare [23, Section 4.1] for a historical discussion.
The iteration of transcendental entire functions \(f:\mathbb {C}\rightarrow \mathbb {C}\) also goes back to Fatou [16], and has received considerable attention in recent years. As in the rational case, the Fatou set \(F(f)\subset \mathbb {C}\) of such a function is defined as the set of \(z\in \mathbb {C}\) such that the iterates \(\{f^n\}_{n\in \mathbb {N}}\) form a normal family in a neighbourhood of z. Its complement, the Julia set \(J(f):= \mathbb {C}{\setminus } F(f)\), is the set where the dynamics is “chaotic”. The role played by the set of critical values in rational dynamics is now taken on by the set S(f) of (finite) singular values, i.e. the closure of the set of critical and asymptotic values of f (see Sect. 2).
In the transcendental setting—due to the effect of the non-compactness of the phase space and the essential singularity at infinity—it is not clear how “hyperbolicity” should be defined. Accordingly, there is currently no accepted general definition; see Appendix A for a brief historical discussion. We propose the following notion of “expansion” in this setting.
Definition 1.1
(Expanding entire functions) A transcendental entire function f is expanding if there exist a connected open set \(W\subset \mathbb {C}\), which contains J(f), and a conformal metric \(\rho =\rho (z)|\mathrm{d}z|\) on W such that:
-
(1)
W contains a punctured neighbourhood of infinity, i.e. there exists \(R>0\) such that \(z\in W\) whenever \(|z|>R\);
-
(2)
f is expanding with respect to the metric \(\rho \), i.e. there exists \(\lambda >1\) such that
$$\begin{aligned} \Vert \mathrm{D}f(z)\Vert _{\rho } := |f'(z)|\cdot \frac{\rho (f(z))}{\rho (z)} \ge \lambda \end{aligned}$$whenever \(z,f(z)\in W\); and
-
(3)
the metric \(\rho \) is complete at infinity, i.e. \({\text {dist}}_\rho (z, \infty ) = \infty \) whenever \(z \in W\).
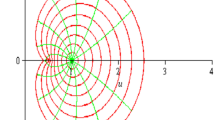
Entire functions that are expanding on a neighbourhood of the Julia set, but should not be considered hyperbolic. The functions \(f_1(z) = z+1+e^{-z}\), \(f_2(z)=z-1+e^{-z}\) and \(f_3(z) = z-1 + 2\pi i + e^{-z}\) can be seen to be expanding on neighbourhoods (in \(\mathbb {C}\)) of their Julia sets (shown in black). \(f_1\) has a Baker domain, \(f_2\) has infinitely many superattracting fixed points and \(f_3\) has wandering domains. None of the functions \(f_p\) is stable under perturbations within the family \(z\mapsto \lambda f_p\), \(\lambda \in \mathbb {C}\). See Appendix B for details, and compare also Fig. 2
We make three remarks about this definition. First we note that the final condition holds whenever the metric \(\rho \) is complete. Indeed, as we shall see below, we could require that \(\rho \) is complete without changing the class of expanding functions. We prefer instead to use the weaker condition (3), which allows \(\rho \) to be the Euclidean metric.
Second, one might ask, in analogy to hyperbolicity for rational maps, for the metric \(\rho \) to be defined and conformal on a full (rather than punctured) neighbourhood of \(\infty \). However, due to the nature of the essential singularity at infinity, such expansion can never be satisfied; see Corollary 1.6 below.
Finally, one might require only expansion on a neighbourhood of the Julia set, as a subset of the complex plane. This is too weak a condition. Functions with this property may have infinitely many attractors, wandering domains or Baker domains: invariant domains of normality in which all orbits converge to infinity. (Compare Fig. 1.) Such behaviour is not compatible with the usual picture of hyperbolicity and, moreover, usually not stable even under simple perturbations (see Fig. 2).
Our key observation about expanding entire functions is the following:
Theorem 1.2
(Expansion only in the Eremenko–Lyubich class) If f is expanding in the sense of Definition 1.1, then S(f) is bounded.
In other words, every expanding function belongs to the Eremenko–Lyubich class
Introduced in [14], \(\mathcal {B}\) is a large and well-studied class. For functions \(f\in \mathcal {B}\) there is a natural and well-established notion of hyperbolicity. Indeed, already McMullen [22, Section 6] suggested calling an entire function f “expanding” if the postsingular set \(P(f)\subset S(f)\) is a compact subset of the Fatou set (see condition (d) in Theorem 1.3 below). The expansion property he established for such a function f [22, Proposition 6.1] is non-uniform, but Rippon and Stallard [25, Theorem C] established that Definition 1.1 holds for \(f^n\), with \(\rho \) the cylinder metric, and n sufficiently large. In [24, Lemma 5.1], it is shown that f itself satisfies Definition 1.1 with respect to a suitable hyperbolic metric.
Note that the expanding property is stated in [25, Theorem C] only for points in the Julia set, but holds also on the preimage of a neighbourhood of \(\infty \) by a well-known estimate of Eremenko and Lyubich; see (1.1) below or [25, Lemma 2.2]. We also remark that Rippon and Stallard treat the more general case of transcendental meromorphic functions. While we restrict here to entire functions, where Definition 1.1 seems particularly natural, our methods apply equally to the meromorphic case; compare Theorem 1.4 and the discussion in Appendix A.
Rippon and Stallard [25, p. 3253] mention that—while it is not clear what the definition of a hyperbolic transcendental entire (or meromorphic) function should be—it is natural to call the above functions “hyperbolic” in view of their expansion properties. Our results suggest that, conversely, only these entire functions should be classed as hyperbolic.
Theorem and Definition 1.3
(Hyperbolic entire functions) All of the following properties of a transcendental entire function \(f:\mathbb {C}\rightarrow \mathbb {C}\) are equivalent. If any, and hence all, of these conditions hold, then f is called hyperbolic.
-
(a)
f is expanding in the sense of Definition 1.1;
-
(b)
f is expanding in the sense of Definition 1.1, and (for suitably chosen W) the metric \(\rho \) can be chosen to be the hyperbolic metric on W;
-
(c)
\(f\in \mathcal {B}\) and every singular value belongs to the basin of an attracting periodic cycle;
-
(d)
the postsingular set
$$\begin{aligned} P(f) := \overline{\bigcup _{n\ge 0} f^n(S(f))} \end{aligned}$$is a compact subset of F(f).
Moreover, each hyperbolic function is stable within its quasiconformal equivalence class.
Remark
Quasiconformal equivalence classes form the natural parameter spaces of transcendental entire functions. (See Proposition 3.2 for the formal meaning of the final statement in the theorem). These classes were defined implicitly by Eremenko and Lyubich [14], and explicitly by the first author [24], and provide the appropriate context in which to consider stability.
Expansion near infinity It is well-known that functions in the Eremenko–Lyubich class have strong expansion properties near infinity. Indeed, if \(f\in \mathcal {B}\), then Eremenko and Lyubich [14, Lemma 1] proved that
Observe that this quantity is precisely the derivative of f with respect to the cylindrical metric \(|\mathrm{d}z|/|z|\) on the punctured plane. The second author [26] showed that the converse also holds: no function outside of class \(\mathcal {B}\) exhibits this type of expansion near infinity. More precisely:
Theorem A
(Characterisation of class \(\mathcal {B}\)) Suppose that f is a transcendental entire function, and consider the quantity
Then, either \(\eta (f) = \infty \) and \(f\in \mathcal {B}\), or \(\eta (f) = 0\) and \(f\notin \mathcal {B}\).
Theorem 1.2 follows from the following strengthening of Theorem A.
Theorem 1.4
(Shrinking property near infinity) Let f be a transcendental entire (or meromorphic) function and \(s\in S(f)\). Let U be an open neighbourhood of s. Suppose that \(\rho (z)|\mathrm{d}z|\) is a conformal metric defined on \(V:= f^{-1}(U)\) such that \({\text {dist}}_{\rho }(z,\infty )=\infty \) for all \(z\in V\). Then
Note that one obtains the second half of Theorem A by applying Theorem 1.4 to the cylindrical metric and a sequence of singular values tending to infinity. A similar application of Theorem 1.4 gives Theorem 1.2.
Clearly some condition must be imposed upon the metric \(\rho \) to obtain (1.3) when U contains no critical values. Indeed, if we let \(\rho \) be the pull-back of the Euclidean metric under f, then (1.3) fails by definition. However, it appears plausible that such a pull-back must decay rapidly on some approach to infinity, and so the conclusion of Theorem 1.4 holds also for certain metrics that are not complete at infinity. The following theorem, another considerable strengthening of Theorem A, shows that this is indeed the case.
Theorem 1.5
(Metrics with polynomially decaying densities) Let f be a transcendental entire (or meromorphic) function and \(s\in S(f)\). If U is an open neighbourhood of s, then
for all \(\tau >0\).
One obtains the second half of Theorem A from Theorem 1.5 by setting \(\tau =1\). Similarly, one obtains (1.3) with \(\rho \) being the spherical metric by setting \(\tau =2\).
Moreover, if f is transcendental entire, then we can apply Theorem 1.5 to the function 1 / f, the singular value \(s=0\) and \(\tau =2\). As claimed above, this implies that the function f cannot be expanding with respect to the spherical metric on the preimage of a full neighbourhood of \(\infty \).
Corollary 1.6
(No expansion for the spherical metric) Let f be a transcendental entire function, and let \(R>0\). Then
Remark 1.7
Corollary 1.6 can also be seen to follow from Wiman–Valiron theory, which shows that there are points of arbitrarily large modulus near which f behaves like a monomial of arbitrarily large degree. It is straightforward to deduce (1.4) from this fact. (More precisely, the claim follows e.g. from formulae (3) and (4) in the statement of the Wiman–Valiron theorem in [12, p. 340]). We are grateful to Alex Eremenko for this observation.
The Eremenko–Lyubich class on a hyperbolic domain Finally, we consider the analogue of the class \(\mathcal {B}\) for functions analytic in a hyperbolic domain. Suppose that \(\Omega \subset \mathbb {C}\) is a hyperbolic domain (or, more generally, a hyperbolic Riemann surface), and that \(f:\Omega \rightarrow \mathbb {C}\) is analytic. We say that f belongs to the Eremenko–Lyubich class, \(\mathcal {B}\), if the set of singular values of f is bounded. We modify the definition (1.2) as follows:
where the norm of the derivative is evaluated using the hyperbolic metric on \(\Omega \) and the cylindrical metric on the range.
Theorem 1.8
(Class \(\mathcal {B}\) on a hyperbolic surface) Suppose that \(\Omega \) is a hyperbolic surface and that \(f:\Omega \rightarrow \mathbb {C}\) is analytic and unbounded. Then, either \(\eta _{\Omega }(f) = \infty \) and \(f\in \mathcal {B}\), or \(\eta _{\Omega }(f) = 0\) and \(f\notin \mathcal {B}\).
Remark 1.9
For the second part of Theorem 1.8, we could replace the hyperbolic metric by any complete metric on \(\Omega \), as in Theorem 1.4. However, Theorem 1.8 as stated provides an appealing dichotomy in terms of the conformally natural quantity \(\eta _{\Omega } (f)\).
Ideas of the proofs Our proof of Theorem 1.4 considerably simplifies the original proof of Theorem A, and can be summarized as follows. The set V must contain either a critical point of f or an asymptotic curve \(\gamma \) whose image is a line segment in U; this is a classical and elementary fact, but its connection to the questions at hand appears to have been overlooked. Since the \(\rho \)-length of \(\gamma \) is infinite, while the Euclidean length of \(f(\gamma )\) is finite, the conclusion is immediate.
This argument clearly does not apply to metrics that are not complete at infinity, and hence a more detailed analysis is required for the proof of Theorem 1.5. Once again, we rely on elementary mapping properties of functions near a singular value, s, that is not the limit of critical values. We show that there are infinitely many, pairwise disjoint, unbounded simply-connected domains on which the function in question is univalent, and which are mapped to round discs near s; see Corollary 2.9. Using a similar idea as in the classical proof of the Denjoy–Carleman–Ahlfors theorem, it follows that, within some of these domains, the function must tend very quickly towards a corresponding asymptotic value. This leads to the desired conclusion.
Finally, the second part of Theorem 1.8 follows in the same manner as Theorem 1.4. The first part, on the other hand, can be deduced in a similar way to the proof of [14, Lemma 1], although we adopt a slightly different approach using basic properties of the hyperbolic metric.
Structure of the article In Sect. 2 we give background on the notion of singular values, and prove some preliminary results. In Sect. 3, we deduce Theorems 1.2, 1.3 and 1.4. Sections 4 and 5 prove Theorems 1.5 and 1.8. Appendix A contains historical remarks concerning notions of hyperbolicity for entire functions, and Appendix B concerns the functions in Fig. 1.
Basic background and notation We denote the complex plane, the Riemann sphere and the unit disc by \(\mathbb {C}\), \(\widehat{\mathbb {C}}\) and \(\mathbb {D}\) respectively. For Euclidean discs, we use the notation
If X is a Riemann surface, then we denote by \(\infty _X\) the added point in the one-point compactification of X. Hence, if \((z_n)\) is a sequence of points of X which eventually leaves any compact subset of X, then \(\lim _{n\rightarrow \infty } z_n = \infty _X\). (If X is already compact, then \(\infty _X\) is an isolated point of the one-point compactification. This allows for uniformity of statements and definitions).
Closures and boundaries are always taken in an underlying Riemann surface X; which X is meant should be clear from the context.
Suppose that X is a Riemann surface, and \(U\subset X\) is open. A conformal metric on U is a tensor that takes the form \(\rho (z)|\mathrm{d}z|\) in local coordinates, with \(\rho \) a continuous positive function. When \(X = \mathbb {C}\), which is the case of most interest to us, we can express the metric globally in this form, and we do not usually distinguish between the metric and its density function \(\rho (z)\).
If \(\gamma \subset U\) is a locally rectifiable curve, then we denote the length of \(\gamma \) with respect to the metric \(\rho \) by \(\ell _\rho (\gamma )\). If \(z, w \in U\), then we denote the distance from z to w with respect to the metric \(\rho \) by \({\text {dist}}_\rho (z,w)\); i.e. \({\text {dist}}_{\rho }(z,w)=\inf _{\gamma } \ell _{\rho }(\gamma )\), where the infimum is taken over all curves connecting z and w. By definition, this distance is infinite if z and w belong to different components of U. We also define \({\text {dist}}_{\rho }(z,\infty _X):= \liminf _{w\rightarrow \infty _X}{\text {dist}}_{\rho }(z,w)\). By definition, this quantity is infinite if U is relatively compact in X.
If \(z \in X\) and \(S \subset X\), then we also set \({\text {dist}}_\rho (z, S) := \inf _{w \in S} {\text {dist}}_\rho (z,w)\), and define \({\text {diam}}_\rho (S) = \sup _{w_1, w_2 \in S} {\text {dist}}_\rho (w_1, w_2)\). When \(X=\mathbb {C}\) and \(\rho \) is the Euclidean metric, then we write simply \(\ell (\gamma )\), \({\text {dist}}(z,w)\) and \({\text {dist}}(z, S)\).
If X is a hyperbolic surface, then we write \(\rho _X\) for the hyperbolic metric on X and, in local coordinates, denote its density function by \(\rho _X(z)\).
2 Singular values
In this section, we first review the definitions of singular values. While we apply them mainly for meromorphic functions defined on subsets of the complex plane, we introduce them in the more general setting of analytic functions between Riemann surfaces; see also [10]. We do so to facilitate future reference, and to emphasize the general nature of our considerations. In contrast to previous articles on similar subjects, we do not require Iversen’s more precise classification of inverse function singularities, for which we refer to [5, 6, 19] and also [13]. Instead, we only use elementary mapping properties of functions having singular values, which we derive here from first principles.
Definition 2.1
(Singular values) Let X and Y be Riemann surfaces, let \(f:X\rightarrow Y\) be analytic, and let \(s\in Y\).
-
(a)
s is called a regular value of f if there is an open neighbourhood U of s with the following property: if V is any connected component of \(f^{-1}(U)\), then \(f:V\rightarrow U\) is a conformal isomorphism.
-
(b)
s is called a singular value of f if s is not a regular value.
-
(c)
s is called a critical value of f if it is the image of a critical point.
-
(d)
s is called an asymptotic value of f if there is a curve \(\gamma :[0,\infty )\rightarrow X\) such that \(\gamma (t)\rightarrow \infty _X\) and \(f(\gamma (t))\rightarrow s\) as \(t\rightarrow \infty \). Such \(\gamma \) is called an asymptotic curve.
The sets of singular, critical and asymptotic values of f are denoted by S(f), \({ CV}(f)\) and \({ AV}(f)\) respectively.
Remark 2.2
(Comments on the definition) Clearly \(CV(f)\cup AV(f)\subset S(f)\). On the other hand, critical and asymptotic values are dense in S(f) (see Corollary 2.7 below), so that, in fact, \(S(f)=\overline{AV(f)\cup CV(f)}\).
Equivalently to the definition above, S(f) is the smallest closed subset S of Y such that the restriction \(f:f^{-1}(Y{\setminus } S)\rightarrow Y{\setminus } S\) is a covering map.
Observe that any value in \(Y{\setminus } \overline{f(X)}\) is a regular value of f. For example, if \(X=\mathbb {D}\), \(Y=\mathbb {C}\) and \(f(z):= z\), then the set of singular values of f coincides with the unit circle \(\partial \mathbb {D}\).
The following observation shows that, near any singular value, we can find inverse branches defined on round discs whose boundaries contain either critical or asymptotic values.
Lemma 2.3
(Asymptotic values with well-behaved inverse branches) Let X be a Riemann surface, and let \(f:X\rightarrow \mathbb {D}\) be analytic, but not a conformal isomorphism. Then there exists a round disc D with \(\overline{D}\subset \mathbb {D}\), a branch \(\varphi :D\rightarrow X\) of \(f^{-1}\) defined on D, and a singular value \(s\in \partial D\cap S(f)\) such that either
-
(a)
\(\lim _{z\rightarrow s} \varphi (z)\) is a critical point of f in X, and s is a critical value of f, or
-
(b)
\(\lim _{z\rightarrow s} \varphi (z)=\infty _X\). In particular, s is an asymptotic value of f, and there is an asymptotic curve \(\gamma \) that maps one-to-one onto a straight line segment \(f(\gamma )\) ending at s.
Proof
Fix some point \(z_0\in X\) which is not a critical point of f. By postcomposing with a Möbius transformation, we may assume without loss of generality that \(f(z_0)=0\). Let \(\varphi \) be the branch of \(f^{-1}\) taking 0 to \(z_0\), and let \(r>0\) be the greatest value such that \(\varphi \) can be continued analytically to the disc D of radius r around 0. Then \(r<1\), since f is not a conformal isomorphism. It follows that there is a point \(s\in \partial D\cap \mathbb {D}\) such that \(\varphi \) cannot be continued analytically into s.
If \(\lim _{z\rightarrow s}\varphi (z)=\infty _X\), then we can take \(\gamma =\varphi (L)\), where L is the radius of D ending at s, and the proof of case (b) is complete. Otherwise, there is a sequence \(z_n\in D\) with \(z_n\rightarrow s\) and \(\varphi (z_n)\rightarrow c\), for some \(c\in X\). By continuity of f, we have \(f(c)=s\). Moreover c is a critical point, since otherwise the local inverse of f that maps s to c would provide an analytic continuation of \(\varphi \) into s by the identity theorem. \(\square \)
Discs as in Lemma 2.3, on which branches of the inverse are defined and which have asymptotic values on their boundary, have appeared previously in the study of indirect asymptotic values in the sense of Iversen; see [5, Proof of Theorem 1] or [29, Theorem 6.2.3]. To simplify subsequent discussions, we introduce the following terminology.
Definition 2.4
(Discs of univalence) Let X and Y be Riemann surfaces, and let \(f:X\rightarrow Y\) be analytic. Suppose that D is an analytic Jordan domain such that \(\overline{D} \subset Y\), and that \(\varphi :D\rightarrow X\) is a branch of \(f^{-1}\) defined on D. Suppose furthermore that there is an asymptotic value \(s\in \partial D\) such that \(\lim _{z\rightarrow s} \varphi (z)=\infty _X\).
Then we call D a disc of univalence at the asymptotic value s. We also call the domain \(V:= \varphi (D)\subset X\) a tract over the disc of univalence D.
Remark 2.5
(Asymptotic curves with well-behaved images) Observe that, if s is an asymptotic value for which there exists a disc of univalence, then in particular there is an asymptotic curve \(\gamma \) for s that is mapped one-to-one to an analytic arc compactly contained in Y, with one endpoint at s.
The following observation is frequently useful.
Observation 2.6
(Discs of univalence for a restriction) Let X and Y be Riemann surfaces, and let \(f:X\rightarrow Y\) be analytic. Let \(U\subset Y\) be a domain, and let W be a connected component of \(f^{-1}(U)\). Then any disc of univalence of the restriction \(f:W\rightarrow U\) at an asymptotic value \(s\in U\) is also a disc of univalence of \(f:X\rightarrow Y\) at s.
Proof
Let \(\varphi :D\rightarrow V \subset W\) be a branch of \(f^{-1}\) as in the definition of the disc of univalence D. Then \(\lim _{z\rightarrow s} \varphi (z) = \infty _W\). Since W was chosen to be a connected component of \(f^{-1}(U)\), and so \(f(\partial W)\subset \partial U\), we deduce that \(\lim _{z\rightarrow s} \varphi (z) = \infty _X\). \(\square \)
Corollary 2.7
(Critical and asymptotic values are dense) Let X and Y be Riemann surfaces, and let \(f:X\rightarrow Y\) be analytic. Denote by \(\widetilde{AV}(f)\) the set of those asymptotic values at which there exists a disc of univalence. Then \(\widetilde{AV}(f)\cup CV(f)\) is dense in S(f).
Proof
Let \(s\in S(f)\), and let U be a simply-connected neighbourhood of s. By definition, there exists a connected component V of \(f^{-1}(U)\) such that \(f:V\rightarrow U\) is not a conformal isomorphism. Applying Lemma 2.3 to \(F := \varphi \circ (f|_V)\), where \(\varphi :U\rightarrow \mathbb {D}\) is a Riemann map, we find that either U contains a critical point of f, or that F, and hence \(f:V\rightarrow U\), has a disc of univalence. The claim follows from Observation 2.6. \(\square \)
We also note the following well-known fact.
Lemma 2.8
(Isolated singular values) Let X and Y be Riemann surfaces, and let \(f:X\rightarrow Y\) be analytic. Let s be an isolated point of S(f), let U be a simply-connected neighbourhood of s with \(U \cap CV(f) = \emptyset \), and let V be a connected component of \(f^{-1}(U\setminus \{s\})\). Then either
-
(a)
V is a punctured disc, and \(f:V\rightarrow U{\setminus }\{s\}\) is a finite-degree covering map, or
-
(b)
V is simply-connected, and \(f:V\rightarrow U{\setminus }\{s\}\) is a universal covering map.
Proof
By definition, \(f:V\rightarrow U{\setminus }\{s\}\) is a covering map, and the only analytic coverings of the punctured disc are as stated [17, Theorem 5.10]. \(\square \)
We can now establish the following, which is crucial for the proof of Theorem 1.5.
Corollary 2.9
(Disjoint tracts over discs of univalence) Let X and Y be Riemann surfaces, and let \(f:X\rightarrow Y\) be analytic, with no removable singularities at any punctures of X. Let \(s\in S(f)\), and suppose that s has an open neighbourhood U with \(U\cap CV(f)=\emptyset \). Then there exist infinitely many discs of univalence \(D_i\subset U\) of f such that the corresponding tracts \(T_i\) are pairwise disjoint.
Proof
If s is not an isolated point of S(f), then the claim follows immediately from Corollary 2.7.
Otherwise, let \({\tilde{D}}\) be a round disc around s in a given local chart, and apply Lemma 2.8. By assumption, s is not a critical value, and f does not have any removable singularities. Hence, if V is any connected component of \(f^{-1}({\tilde{D}})\), then \(f:V\rightarrow {\tilde{D}}{\setminus } \{s\}\) is a universal covering. We may thus choose a single disc \(D\subset {\tilde{D}}\) that is tangent to s, set \(D_i=D\) for all i, and let the \(T_i\) be the infinitely many different components of \(f^{-1}(D)\) in X. \(\square \)
3 Proofs of Theorems 1.2, 1.3 and 1.4
The following is a general result concerning behaviour of analytic functions on sets that map close to singular values.
Proposition 3.1
(Analytic functions contract when mapping near singular values) Let X and Y be Riemann surfaces, let \(f:X\rightarrow Y\) be analytic, let \(s\in S(f)\), and let U be an open neighbourhood of s. Suppose that V is a connected component of \(f^{-1}(U)\) such that \(f:V\rightarrow U\) is not a conformal isomorphism, and that \(\rho \) is a conformal metric on V such that \({\text {dist}}_\rho (z,\infty _X)=\infty \) for all \(z\in V\). Also let \(\sigma \) be any conformal metric on U. Then
where the norm of the derivative is measured with respect to the metrics \(\rho \) and \(\sigma \).
Proof
Suppose, by way of contradiction, that \(\inf _{z\in V} \Vert \mathrm{D}f(z)\Vert > 0.\) Then f has no critical points in V. By Corollary 2.7 and Remark 2.5, there is an analytic curve \(\gamma \subset V\) to infinity such that \(\gamma \) is mapped one-to-one to an analytic arc L compactly contained in U. Then
\(\square \)
Proof of Theorem 1.4
This follows immediately from Proposition 3.1, by taking \(\sigma \) to be the Euclidean metric. \(\square \)
Remark
In particular, Theorem 1.4, remains true if we replace the full preimage V by any component on which f is not a conformal isomorphism.
Proof of Theorems 1.2 and 1.3
Let f be a transcendental entire function, and let \(\rho \) be a conformal metric, defined on an open neighbourhood W of J(f) that contains a punctured neighbourhood of \(\infty \). Suppose that \({\text {dist}}_{\rho }(z,\infty )=\infty \) for all \(z\in W\), and that f is expanding with respect to the metric \(\rho \). If c is a critical point of f, then either \(c\notin W\) or \(f(c)\notin W\). It follows that W contains only finitely many critical values, none of which lie in J(f). By shrinking W, we may hence assume that W contains no critical values of f.
Claim 1
We have \(W\cap S(f)=\emptyset \). In particular, S(f) is bounded.
Proof
Let \(w\in W\) and let \(R>0\) be such that \(A_R := \{z\in \mathbb {C}:|z|>R\}\subset W\). Since w is not a critical value of f, if \(D\subset W\) is a sufficiently small disc around w, then every component of \(f^{-1}(D)\) that is not contained in \(A_R\) is mapped to D as a conformal isomorphism. On the other hand, every component V of \(f^{-1}(D)\) that is contained in \(A_R\subset W\) is also mapped as a conformal isomorphism, by Proposition 3.1 and the expanding property of f. \(\bigtriangleup \)
Observe that this proves Theorem 1.2.
Claim 2
We have \(J(f)\cap P(f)=\emptyset \).
Proof
Let us set
Then \(\delta _0>0\) since W contains a punctured neighbourhood of \(\infty \), and by assumption on \(\rho \).
Let \(w\,{\in }\, J(f)\), and let \(\Delta _0\) be a simply-connected neighbourhood of w chosen so small that \({\text {diam}}_{\rho }(\Delta _0)<\delta _0\). By Claim 1, \(\Delta _0 \cap S(f)=\emptyset \), and hence every component \(\Delta _1\) of \(f^{-1}(\Delta _0)\) is mapped to \(\Delta _0\) as a conformal isomorphism. Furthermore, by the expanding property of f, we have \({\text {diam}}_{\rho }(\Delta _1) < \delta _0\). Hence we can apply the preceding observation to \(\Delta _1\), and see that any component of \(f^{-2}(\Delta _0)\) is mapped univalently to \(\Delta _0\).
Proceeding inductively, we see that every branch of \(f^{-n}\) can be defined on \(\Delta _0\), for all \(n\ge 0\). Hence \(\Delta _0\cap P(f)=\emptyset \), and in particular \(w\notin P(f)\), as required. \(\bigtriangleup \)
Recall that every parabolic periodic cycle of a transcendental entire function, and the boundary of every Siegel disc, lies in \(J(f)\cap P(f)\) [4, Theorem 7]. Furthermore, any limit function of the iterates of f on a wandering domain is a constant in \(( P(f)\cap J(f))\cup \{\infty \}\) [7]. By Claim 2, \(P(f)\cap J(f)=\emptyset \), and since \(f\in \mathcal {B}\), f has no Fatou component on which the iterates converge locally uniformly to infinity [14, Theorem 1].
Thus we conclude that F(f) is a union of attracting basins, and hence every point of \(S(f)\subset \mathbb {C}{\setminus } W\subset F(f)\) belongs to an attracting basin. This completes the proof that (a) implies (c) in Theorem 1.3.
The equivalence of (c) and (d) is well-known; see e.g. [25] or [8, Section 2]. That these in turn imply expansion in the sense of Definition 1.1, with \(\rho \) the hyperbolic metric on a suitable domain W, was shown in [24, Lemma 5.1]. The final claim regarding stability is made precise by Proposition 3.2 below. \(\square \)
Proposition 3.2
(Stability of hyperbolic functions) Suppose that \(\Lambda \) is a complex manifold, and that \((f_{\lambda })_{\lambda \in \Lambda }\) is a family of entire functions of the form \(f_{\lambda } = \psi _{\lambda }\circ f\circ \varphi _{\lambda }^{-1}\), where \(\varphi _{\lambda },\psi _{\lambda }:\mathbb {C}\rightarrow \mathbb {C}\) are quasiconformal homeomorphisms depending analytically on the parameter \(\lambda \) and f is transcendental entire. If \(\lambda _0\in \Lambda \) is a parameter for which \(f_{\lambda _0}\) is hyperbolic, then \(f_{\lambda _0}\) and \(f_{\lambda }\) are quasiconformally conjugate on their Julia sets whenever \(\lambda \) is sufficiently close to \(\lambda _0\). Moreover, this conjugacy depends analytically on the parameter \(\lambda \).
Proof
Let us first observe that hyperbolicity is an open property in any such family. Indeed, (c) in Theorem 1.3 is equivalent to the existence of a compact set K with \(f(K)\cup S(f)\subset {\text {int}}(K)\); see [8, Proposition 2.1]. Clearly, any function \({\tilde{f}}\) that is sufficiently close to f in the sense of locally uniform convergence satisfies \({\tilde{f}}(K)~\subset ~{\text {int}}(K)\). If, furthermore, \(S({\tilde{f}})\) is sufficiently close to S(f) in the Hausdorff metric, then \(S({\tilde{f}})~\subset ~{\text {int}}(K)\), and hence \({\tilde{f}}\) is also hyperbolic.
Therefore, if f belongs to any analytic family as in the statement of the theorem, then f has a neighbourhood in which all maps are hyperbolic. In particular, no function in this neighbourhood has any parabolic cycles, and it follows that the repelling periodic points of f move holomorphically over this neighbourhood. By the “\(\lambda \)-lemma” [20], it follows that the closure of the set of repelling periodic points of f, i.e. the Julia set, also moves holomorphically. This yields the desired result.
We note that this argument uses the fact that the analytic continuation of a repelling periodic point encounters only algebraic singularities within a family as above. This is proved in [14, Section 4] for maps with finite singular sets; the same argument applies in our setting. Alternatively, the claim can also be deduced formally from the results of [24], where it is shown that, for a given compact subset of the quasiconformal equivalence class, the set of points whose orbits remain sufficiently large moves holomorphically. \(\square \)
4 Metrics decaying at most polynomially
Proof of Theorem 1.5
Let f be a transcendental entire or meromorphic function, let \(s\in S(f)\) be a finite singular value of f, and let U be an open neighbourhood of s. We may assume that there is a disc \(D\subset U\) around s that contains no critical values of f, as otherwise there is nothing to prove.
Let K be any positive integer. By Corollary 2.9, we can find K discs of univalence \(D_1,\dots ,D_K\subset D\), having pairwise disjoint tracts \(G_1,\dots ,G_K\). Let \(a_1,\dots a_K\) be the associated asymptotic values. Also, for \(1\le n \le K\), let \(\Gamma _n\) be the preimage in \(G_n\) of the radius of \(D_n\) ending at \(a_n\).
Then \(\Gamma _n\) is an asymptotic curve for \(a_n\), \(f(\Gamma _n)\) is a straight line segment, and \(f(z)\rightarrow a_n\) as \(z\rightarrow \infty \) in \(\Gamma _n\). This is precisely the setting of the proof of [5, Theorem 1], and formula (12) in that paper shows that there exist an integer n and a sequence \((w_j)\) of points tending to infinity on \(\Gamma _n\) such that
where p is any positive integer with \(4p+3<K\). (In [5], the function f is required to have order less than \(p-3\), and the values \(a_j\) are assumed to be pairwise distinct. However, neither of these assumptions are required for the proof of formula (12)). Since K was arbitrary, the claim of the theorem follows.
The argument in [5] is essentially the same as in the proof of the classical Denjoy–Carleman–Ahlfors theorem: since the tracts \(G_n\) are unbounded and pairwise disjoint, some of them must have a small average opening angle. By the Ahlfors distortion theorem, it follows that f must approach \(a_n\) rapidly along \(\Gamma _n\), which is only possible if the derivative becomes quite small along this curve.
For the reader’s convenience, we present a self-contained proof of Theorem 1.5, following the same idea. Since we are not interested in precise estimates, we replace the use of the Ahlfors distortion theorem by the standard estimate on the hyperbolic metric in a simply-connected domain. Let \(R_0>1\) be sufficiently large to ensure that each \(\Gamma _n\) contains a point of modulus \(R_0\). For each n, and each \(z\in \Gamma _n\), let us denote by \(\Gamma _n^+(z)\) the piece of \(\Gamma _n\) connecting z to \(\infty \), and the complementary bounded piece by \(\Gamma _n^-(z)\).
Suppose that the conclusion of the theorem did not hold. Then
for some \(\tau >1\) and all \(z\in \bigcup \Gamma _n\). This implies
We now prove that, if K was chosen large enough, depending on \(\tau \), then such an estimate cannot hold for all \(\Gamma _n\). Indeed, for \(x \ge R_0\), let \(\vartheta _n(x)\) denote the angular measure of the set \(\{\vartheta :xe^{i\vartheta }\in G_n\}\). Since the \(G_n\) are disjoint, we have
We are interested in the reciprocals \(1/\vartheta _n(x)\), since these allow us to estimate the density of the hyperbolic metric in \(G_n\). Indeed, for \(|z|\ge R_0\), it follows from the fact that \(G_n\) is simply connected and [9, Theorem I.4.3] that
By (4.2) and the Cauchy–Schwarz inequality, we have
Let \(x\ge R_0\) and, for each n, choose a point \(z_{n}\in \Gamma _n\) with \(|z_n|=x\). Then the total hyperbolic length of the pieces \(\Gamma _n^-(z_n)\) satisfies
Thus there must be a choice of n and a sequence \(w_j\rightarrow \infty \) in \(\Gamma _n\) such that
as \(j\rightarrow \infty \). Now \(f:G_n\rightarrow D_n\) is a conformal isomorphism. Since \(f(\Gamma _n^-(w_j))\) is a radial segment connecting the centre of \(D_n\) to \(f(w_j)\), we deduce that
Hence we see that (4.1) cannot hold for \(\tau < 1 + K/(4\pi )\). Since K was arbitrary, this completes the proof. \(\square \)
Remark 4.1
We could have formulated a more general version of Theorem 1.5, where f is an analytic function between Riemann surfaces X and Y, and \(\rho \) is a conformal metric on X that is complete except at finitely many punctures of X, where the metric is allowed to decay at most polynomially.
5 The Eremenko–Lyubich class on a hyperbolic surface
Proof of Theorem 1.8
Let \(\Omega \) be a hyperbolic surface, and let \(f:\Omega \rightarrow \mathbb {C}\) be analytic. First suppose that S(f) is unbounded. For every \(R>0\), we may apply Proposition 3.1 to f, taking s to be an element of S(f) with \(|s|>R\), taking \(\rho \) to be the hyperbolic metric on \(\Omega \), and \(\sigma \) the cylindrical metric on \(\mathbb {C}\). The fact that \(\eta _{\Omega }(f)=0\) follows.
On the other hand, suppose that S(f) is bounded, and let \(R_0 > \max _{s\in S(f)}|s|\). Consider the domain \(U := \{z\in \mathbb {C}:|z|>R_0\}\), and its preimage \(\mathcal {V}:= f^{-1}(U)\). If V is a connected component of \(\mathcal {V}\), then \(f:V\rightarrow U\) is an analytic covering map, and hence a local isometry of the corresponding hyperbolic metrics.
By the Schwarz lemma [9, Theorem I.4.2], we know that \(\rho _V \ge \rho _\Omega \). On the other hand, the density of the hyperbolic metric of U is given by [18, Example 9.10]
as \(z\rightarrow \infty \). Hence the derivative of f, measured with respect to the hyperbolic metric on \(\Omega \) and the cylindrical metric on \(\mathbb {C}\), satisfies
as \(|f(z)|\rightarrow \infty \) (where the second term should be understood in a local coordinate for \(\Omega \) near z). Hence \(\eta _{\Omega }(f)=\infty \), as claimed. \(\square \)
References
Badeńska, A.: Real analyticity of Jacobian of invariant measures for hyperbolic meromorphic functions. Bull. Lond. Math. Soc. 40(6), 1017–1024 (2008)
Baker, I.N.: Wandering domains in the iteration of entire functions. Proc. Lond. Math. Soc. (3) 49(3), 563–576 (1984)
Beardon, A.F.: Iteration of rational functions. Graduate Texts in Mathematics, vol. 132. Springer, New York (1991)
Bergweiler, W.: Iteration of meromorphic functions. Bull. Am. Math. Soc. (N.S) 29(2), 151–188 (1993)
Bergweiler, W., Eremenko, A.È.: On the singularities of the inverse to a meromorphic function of finite order. Rev. Mat. Iberoamericana 11(2), 355–373 (1995)
Bergweiler, W., Eremenko, A.È.: Direct singularities and completely invariant domains of entire functions. Ill. J. Math. 52(1), 243–259 (2008)
Bergweiler, W., Harut, M., Kriete, H., Meier, H.G., Terglane, N.: On the limit functions of iterates in wandering domains. Ann. Acad. Sci. Fenn. Ser. A I Math. 18(2), 369–375 (1993)
Bergweiler, W., Fagella, N., Rempe-Gillen, L.: Hyperbolic entire functions with bounded Fatou components. Comment. Math. Helv. 90(4), 799–829 (2015)
Carleson, L., Gamelin, T.W.: Complex dynamics. Universitext: Tracts in Mathematics. Springer, New York (1993)
Epstein, A.: Towers of finite type complex analytic maps, Ph.D. thesis, City University of New York (1995)
Epstein, A., Oudkerk, R.: Iteration of Ahlfors and Picard functions which overflow their domains (Manuscript)
Eremenko, A.È., On the iteration of entire functions, Dynamical systems and ergodic theory (Warsaw, : Banach Center Publ., vol. 23. PWN, Warsaw 1989, 339–345 (1986)
Eremenko, A.È.: Singularities of inverse functions. Lecture notes from the 2013 ICMS conference ‘The role of complex analysis in complex dynamics’. http://www.icms.org.uk/downloads/Complex/Eremenko
Eremenko, A.È., Lyubich, MYu.: Dynamical properties of some classes of entire functions. Ann. Inst. Fourier (Grenoble) 42(4), 989–1020 (1992)
Fatou, P.: Sur les équations fonctionnelles, II. Bull. Soc. Math. Fr. 48, 33–94 (1920)
Fatou, P.: Sur l’itération des fonctions transcendantes entières. Acta Math. 47, 337–370 (1926)
Forster, O.: Lectures on Riemann surfaces. Springer, New York (1999)
Hayman, W.K.: Subharmonic functions. Vol. 2, London Mathematical Society Monographs, vol. 20, Academic Press Inc. [Harcourt Brace Jovanovich Publishers], London (1989)
Iversen, F.: Recherches sur les fonctions inverses des fonctions méromorphes., Ph.D. thesis, Helsingfors (1914)
Mañé, R., Sad, P., Sullivan, D.: On the dynamics of rational maps. Ann. Sci. École Norm. Sup. (4) 16(2), 193–217 (1983)
Mayer, V., Urbański, M.: Thermodynamical formalism and multifractal analysis for meromorphic functions of finite order. Mem. Amer. Math. Soc. 203 no. 954, vi+107 (2010)
McMullen, C.T.: Area and Hausdorff dimension of Julia sets of entire functions. Trans. Am. Math. Soc. 300(1), 329–342 (1987). MR871679 (88a:30057)
McMullen, C.T.: Complex dynamics and renormalization. Annals of Mathematics Studies, vol. 135. Princeton University Press, Princeton (1994)
Rempe, L.: Rigidity of escaping dynamics for transcendental entire functions. Acta Math. 203(2), 235–267 (2009)
Rippon, P.J., Stallard, G.M.: Iteration of a class of hyperbolic meromorphic functions. Proc. Am. Math. Soc. 127(11), 3251–3258 (1999)
Sixsmith, D.J.: A new characterisation of the Eremenko–Lyubich class. J. Anal. Math. 123, 95–105 (2014)
Smale, S.: Differentiable dynamical systems. Bull. Am. Math. Soc. 73, 747–817 (1967)
Weinreich, J.: Boundaries which arise in the iteration of transcendental entire functions., Ph.D. thesis, Imperial College (1990)
Zheng, J-H.: Value distribution of meromorphic functions, Tsinghua University Press, Beijing; Springer, Heidelberg (2010)
Zheng, J-H.: Dynamics of hyperbolic meromorphic functions. Discrete Contin. Dyn. Syst. 35(5), 2273–2298 (2015)
Acknowledgements
We would like to thank Walter Bergweiler and Alex Eremenko for interesting discussions about the possibility of strengthening and extending Theorem A, which led us to discover the results presented in this article. Rempe-Gillen was supported by a Philip Leverhulme Prize. Sixsmith was supported by Engineering and Physical Sciences Research Council grant EP/J022160/1.
Author information
Authors and Affiliations
Corresponding author
Additional information
To Alex Eremenko on the occasion of his 60th birthday.
Appendices
Appendix A: Definitions of hyperbolicity
As mentioned in the introduction, the first notion of “expanding” entire functions, which coincides with our notion of hyperbolicity in Definition 1.3, goes back to McMullen [22]. As also mentioned, Rippon and Stallard [25] discuss hyperbolicity in the transcendental setting, arguing that functions in the class \(\mathcal {B}\) satisfying (c) in Theorem 1.3 deserve to be called hyperbolic. However, they left open the possibility that other functions might also be classed as “hyperbolic”.
Mayer and Urbanski [21] gave a definition of hyperbolicity that relies on the Euclidean metric. Specifically, they require both uniform expansion on the Julia set and that the postsingular set be a definite (Euclidean) distance away from the Julia set. Without additional requirements, this includes such functions as our examples in the introduction, which exhibit “non-hyperbolic” phenomena and are not stable under simple perturbations; see Appendix B.
With an additional strong regularity assumption near the Julia set, Mayer and Urbanski obtained striking and powerful results concerning the measurable dynamics of “hyperbolic” functions in the above sense; further properties of these functions are described in [1]. We are, however, not aware of any examples outside of the class \(\mathcal {B}\) where these assumptions are known to hold. On the other hand, if \(f\in \mathcal {B}\) is hyperbolic in the sense of Mayer and Urbanski, then it is also hyperbolic in the sense of Theorem 1.3.
All of these definitions are in fact formulated, more generally, for transcendental meromorphic functions. In this setting, there is a third, and strongest, notion of hyperbolicity, studied by Zheng [30]. This requires, in addition, that infinity is not a singular value, and hence can never be satisfied when f is transcendental entire. An example of a function with this property is \(f(z) = \lambda \tan z\), for \(\lambda \in (0, 1)\). (We note that Zheng also studied the definitions given by Rippon and Stallard and by Mayer and Urbanski; we refer to his paper for further details).
Zheng’s definition of “hyperbolicity on the Riemann sphere” may be considered to correspond most closely to the case of hyperbolic rational functions. In particular, Zheng shows that a meromorphic function is hyperbolic in this sense if and only if it satisfies a certain uniform expansion property with respect to the spherical metric.
Our results also apply in the setting of meromorphic functions, with appropriate modifications of definitions to correctly handle prepoles. Once again, they indicate that the notion of hyperbolicity does not make sense outside of the class \(\mathcal {B}\).
We recall also our earlier comment that, although our applications are to meromorphic functions on subsets of the complex plane, our basic results regarding the properties of singularities are given for analytic functions between Riemann surfaces. A generalisation of the study of transcendental dynamics into this setting is possible for the classes of “finite type maps”, and more generally “Ahlfors islands maps”, suggested by Epstein [10, 11]. If W is a Riemann surface and X is a compact Riemann surface, then an analytic function \(f:W\rightarrow X\) is called a finite-type map if S(f) is finite and f has no removable singularities at any punctures of W. In the case where \(W\subset X\), Epstein develops an iteration theory that carries over the basic results from the theory of rational dynamics and of entire and meromorphic functions with finitely many singular values.
Similarly to the case of meromorphic functions, we could again consider two different notions of hyperbolicity in this setting: one, analogous to that of Zheng, where all singular values must lie in attracting basins or map outside of the closure of W; and a weaker notion, in analogy to that of Rippon and Stallard, where we allow singular values to lie on (or map into) the boundary of the domain of definition. All the standard results for the case of meromorphic functions should extend to this setting also.
The larger class of Ahlfors islands maps includes all transcendental meromorphic functions, as well as all finite type maps. It is tempting to define an “Eremenko–Lyubich class” of such maps, consisting of those for which \(S(f)\cap W\) is a compact subset of the domain of definition W. Our results still apply in this setting, and imply that hyperbolicity is only to be found within this class. However, it is no longer clear that functions within this class have suitable expansion properties near the boundary, and hence dichotomies such as that of Theorem A break down. Finding a natural class that extends both the Eremenko–Lyubich class of entire functions and all finite type maps appears to be an interesting problem.
Appendix B: Expansion near the Julia set for non-hyperbolic functions
In this section, we briefly discuss the three functions
mentioned in the introduction. All three are well-studied, and have properties that are not compatible with what would normally be considered hyperbolic behaviour.
Proposition B.1
(Dynamical properties of the functions \(f_p\))
-
(a)
\(f_1\) has a Baker domain containing the right half-plane \(H := \{ z :{\text {Re }}(z) > 0\}\). That is, \(f_1(H)\subset H\), and \(f^n(z)\rightarrow \infty \) for all \(z\in H\);
-
(b)
\(f_2\) has infinitely many superattracting fixed points, \(z_n := 2\pi i n\);
-
(c)
\(f_3\) has \(J(f_3)=J(f_2)\), and possesses an orbit of wandering domains.
Proof
The function \(f_1\) was first studied by Fatou. The stated property is well-known and can be verified by an elementary calculation.
The function \(f_2\) is precisely Newton’s method for finding the points where \(e^z=1\); it was studied in detail by Weinreich [28]. Clearly it follows directly from the definition that the points \(z_n\) are indeed superattracting fixed points.
Finally, \(f_3\) is a well-known example of a transcendental entire function with wandering domains, first described by Herman; see [2, Example 2 on p. 564] and [4, Section 4.5]. The fact that \(J(f_3)=J(f_2)\) follows easily from the relations \(f_2(z + 2\pi i) = f_2(z) + 2\pi i\) and \(f_3(z) = f_2(z) + 2\pi i\). Since the points \(z_n\) all belong to different Fatou components for \(f_2\), the same is true for \(f_3\). Since \(f_3(z_n)= z_{n+1}\), they do indeed belong to an orbit of wandering domains for \(f_3\). \(\square \)
We now justify the claim, made in the introduction, that these functions are expanding on a complex neighbourhood of the Julia set.
Proposition B.2
(Expansion properties of the functions \(f_p\)) For each \(p\in \{1,2,3\}\), there is an open neighbourhood U of \(J(f_p)\) in \(\mathbb {C}\) with \(f^{-1}(U)\subset U\) and a conformal metric \(\rho \) on U such that \(f_p\) is uniformly expanding with respect to \(\rho \).
Proof
Writing \(w=-e^{-z}\), the function \(f_1\) is semi-conjugate to
This is a hyperbolic entire function, since its unique asymptotic value 0 is an attracting fixed point, and its unique critical point \(-1\) belongs to the basin of attraction of this fixed point. By [24, Lemma 5.1], the function \(F_1\) is expanding on a neighbourhood of its Julia set, with respect to a suitable hyperbolic metric. Pulling back this metric under the semiconjugacy, we obtain the desired property for \(f_1\).
Instability of \(f_1\), illustrating Proposition B.3. Shown are the Julia sets (in black) of \(J(\lambda f_1)\) for two parameter values close to \(\lambda =1\), illustrating Proposition B.3. The second parameter is chosen so that \(f_{\lambda }^2(z_{1000})=\varphi (\lambda )\), as in the proof of the proposition
(We remark that, alternatively, one can show directly that \(f_1\) is expanding with respect to the Euclidean metric, when restricted to a suitable neighbourhood of the Julia set).
The argument for \(f_2\) and \(f_3\) is analogous. Both functions are semi-conjugate to the map
This function is not hyperbolic, as the asymptotic value 0 is a repelling fixed point. However, we note that this asymptotic value does not correspond to any point in the z-plane under the semiconjugacy. One can hence think of \(F_2\) as being hyperbolic as a self-map of \(\mathbb {C}^*=\mathbb {C}{\setminus } \{0\}\), since the critical point \(-1\) is a superattracting fixed point. The same proof as in [24] yields a neighbourhood \({\tilde{U}}\) of \(J(F_2){\setminus }\{0\}\) and a conformal metric on U such that \(F_2\) is expanding, and the claim follows. \(\square \)
Proposition B.3
(Instability of the functions \(f_p\)) Let \(p\in \{1,2,3\}\). Then \(f_p\) is not stable in the family \((\lambda f_p)_{\lambda \in \mathbb {C}}\); more precisely, there exist values of \(\lambda \) arbitrarily close to 1 such that \(\lambda f_p\) and \(f_p\) are not topologically conjugate on their Julia sets.
Proof
We prove only the case \(p=1\); the proofs in the other cases are very similar. For simplicity, we write \(f:= f_1\) and \(f_{\lambda } := \lambda f\). Consider the critical points of \(f_\lambda \), \(z_n := 2n\pi i\). Observe that \(z_n \in F(f)\) for all n. We claim that there are values of \(\lambda \) arbitrarily close to 1 such that, for some sufficiently large value of n, we have \(z_n \in J(f_\lambda )\). In this case J(f) and \(J(f_{\lambda })\) are not topologically conjugate on their Julia sets, since such a conjugacy must preserve the local degree of f.
In order to prove this claim, observe that we can analytically continue the repelling fixed point \(i\pi \) of f as a solution of the equation \(f_{\lambda }(z)=z\) in a neighbourhood of \(\lambda =1\), by the implicit function theorem. That is, if \(\delta \in (0,1)\) is sufficiently small, then there is an analytic function \(\varphi :B(1,\delta ) \rightarrow B(0,2\pi )\) such that \(\varphi (\lambda )\) is a repelling fixed point of \(f_{\lambda }\) for all \(\lambda \in B(1,\delta )\).
It can be seen that there are infinitely many zeros of f, and that we can number a subsequence of them, \((\xi _m)_{m\in \mathbb {N}}\), so that \({\text {Im }}(\xi _m) \rightarrow \infty \) and \({\text {Re }}(\xi _m) \sim -\log ({\text {Im }}(\xi _m))\) as \(m\rightarrow \infty \). By a further calculation, there exists \(r>0\) such that, for sufficiently large values of m, f (and hence \(f_\lambda \)) is univalent in \(B(\xi _m, r)\). Since \(|f_\lambda '(\xi _m)|\rightarrow \infty \) as \(n\rightarrow \infty \), uniformly for \(\lambda \in B(1,\delta )\), we deduce by the Koebe quarter theorem that
for all sufficiently large m, whenever \(\lambda \in B(1, \delta )\).
Suppose that n is large. Observe that the mapping \(\psi _1\) which takes \(\lambda \) to \(f_\lambda (z_n)\) maps \(B(1, \delta )\) to \(B(2+z_n, \delta |2+z_n|)\). Hence, if m is sufficiently large, then n can be chosen such that \( B(\xi _m, r) \subset \psi _1(B(1, \delta )),\) and also \(|\psi _1(\lambda ) - \xi _m| \ge 2r\) whenever \(\lambda \in \partial B(1, \delta )\). Let \(\alpha _\lambda \) be the branch of \(f_\lambda ^{-1}\) which maps B(0, 10) to \(B(\xi _m, r)\).
Suppose that \(\zeta \in B(0, 10)\), and let \(\alpha :B(1, \delta )\rightarrow B(\xi _m, r); \lambda \mapsto \alpha _\lambda (\zeta )\). We deduce by Rouché’s theorem that there exists \(\lambda \in B(1, \delta )\) such that \(\psi _1(\lambda ) - \alpha (\lambda )=0\), which is equivalent to \(f_\lambda ^2(z_n) = \zeta \).
Now consider the mapping \(\psi _2:B(1, \delta ) \rightarrow \mathbb {C}; \lambda \mapsto f_{\lambda }^2(z_n)\). Provided that n is sufficiently large, it follows by the argument above that \(B(0, 10) \subset \psi _2(B(1, \delta ))\).
Let \(K \subset B(1, \delta )\) be a component of \(\psi _2^{-1}(B(0, 10))\). Then
whenever \(\lambda \in \partial K\). Hence we may apply Rouché’s theorem again, and deduce that there exists \(\lambda _0 \in B(1, \delta )\) such that \(\psi _2(\lambda _0) - \varphi (\lambda _0) = 0\). In other words \(f^2_{\lambda _0}(z_n)\) is a repelling fixed point of \(f_{\lambda _0}\) and so lies in \(J(f_{\lambda _0})\). This completes the proof of our claim. \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rempe-Gillen, L., Sixsmith, D. Hyperbolic entire functions and the Eremenko–Lyubich class: Class \(\mathcal {B}\) or not class \(\mathcal {B}\)?. Math. Z. 286, 783–800 (2017). https://doi.org/10.1007/s00209-016-1784-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-016-1784-9