Skip to main content
SpringerLink
Log in

A proof of Sudakov theorem with strictly convex norms

  • Published:
Mathematische Zeitschrift Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

The paper establishes a solution to the Monge problem in \({\mathbb {R}^n}\) for a possibly asymmetric norm cost function and absolutely continuous initial measures, under the assumption that the unit ball is strictly convex—but not necessarily differentiable nor uniformly convex. The proof follows the strategy initially proposed by Sudakov in 1976, found to be incomplete in 2000; the missing step is fixed in the above case adapting a disintegration technique introduced for a variational problem. By strict convexity, mass moves along rays, and we also investigate the divergence of the vector field of rays.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

Id:

The identity function, Id(x) = x

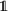S :

The function vanishing out of S, equal to one on S (where \({S\subset \mathbb {R}^n}\))

⦇ a, b ⦈:

The segment in \({\mathbb {R}^n}\) from a to b, without the endpoints

\({[\kern-0.15em[ a, b ]\kern-0.15em]}\) :

The segment in \({\mathbb {R}^n}\) from a to b, including the endpoints

\({\vartriangle}\) :

The symmetric difference between two sets

e k :

{e1, . . . , e n } fixed orthonormal basis of \({\mathbb {R}^n}\)

| · |:

The Euclidean norm of a vector

| · |∞ :

The maximum of the component of a vector

\({\mathcal {B}(X)}\) :

The Borel subsets of \({X\subset\mathbb {R}^n}\)

\({\mathcal {H}^{\alpha}}\) :

The α-dimensional Hausdorff measure in \({\mathbb {R}^n}\)

\({\fancyscript {L}^n}\) :

The Lebesgue measure on \({\mathbb {R}^n}\)

\({\ll}\) :

Denotes that a measure is absolutely continuous w.r.t. another one

\({\langle\cdot\rangle}\) :

Denotes the linear span

\({\langle\cdot,\cdot\rangle}\) :

\({\langle\theta,\varphi\rangle=\int \varphi d\theta}\), where θ is a measure and \({\varphi}\) is θ-integrable

\({\tau_{\sharp}}\) :

The push forward with a measurable map τ, see Appendix A

Π(μ, ν):

The set of transport plans between two probability measures μ and ν

\({f \upharpoonright {S}}\) :

The restriction of the function f to a set S

\({\theta \llcorner {S}}\) :

For A θ-measurable, \({\theta \llcorner {S}(A)=\theta(A \cap S)}\),where S is θ-measurable

\({\int\theta_{s}\, m}\) :

\({\theta=\int\theta_{s}\, dm(s)}\) denotes the disintegration of a measure θ, see Appendix A

μ,ν:

Probability measures on \({\mathbb {R}^n, \mu\ll\fancyscript {L}^n}\)

||·||:

A possibly asymmetric norm on \({\mathbb {R}^n}\) whose unit ball is strictly convex

\({c(x,y)}\) :

The cost function \({c(x,y)=\|y-x\|}\)

D * :

The unit ball \({\{x\in\mathbb {R}^n:\|x\|\leq 1\}}\)

D :

The dual convex set of \({D^{*}\,:\,D=\{\ell\,:\,\ell\cdot v\le 1\quad \forall v {\in} ^{*}\}}\)

∂D :

The boundary of D

δD * :

\({\delta D^*(\ell)=\{v: (\|\ell\|v)\in\partial D}\) and v· ℓ = 1}

\({\varphi}\) :

See Definition 2.1 and (3.1)

\({\mathcal{T}, \mathcal{T}_{\rule[.2pt]{.2pt}{3pt}\!\rm e}}\) :

See Definition 2.2

\({\partial_{c}\phi}\) :

The \({c}\)-subdifferential of \({\phi\,:\, \partial_{c}\phi =\Big\{(x,y):\phi x)-\phi(y)= c(x,y)\Big\}}\)

\({\partial^{-}\phi}\) :

The sub-differential of a function \({\phi:\mathbb {R}^n\mapsto\mathbb {R}: \quad \partial^{-}\phi(x)=\Big\{ v^{*}:\phi(y)\geq \phi(x) +v^{*}\cdot(y-x) \forall y \Big\} }\)

σ·(·):

See Definition 2.11, and also P. 15 for \({\sigma^{\cdot}_{d_{I}}(\cdot)}\)

\({\mathcal {Z}, Z}\) :

Sheaf set and its basis, see Definition 2.9

\({\mathcal {K}}\) :

d-cylinder, see Definition 2.11

\({\mathcal {P}, \mathcal {R}}\) :

See Definition 2.3

\({\mathcal{D}, d}\) :

Directions of the rays, see (2.4) and (2.7)

\({\mathcal {S}}\) :

See Theorems 2.25, 3.2

α:

See Lemma 2.21

\({\tilde\alpha}\) :

See Corollary 2.23, Lemmata 2.21, 2.24

c(t, z):

See Theorem 2.25, Lemma 2.30, (2.23)

References

  1. Ambrosio L., Fusco N., Pallara D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs. The Clarendon Press Oxford University Press, New York (2000)

    Google Scholar 

  2. Ambrosio L., Kirchheim B., Pratelli A.: Existence of optimal transport maps for crystalline norms. Duke Math. J. 125(2), 207–241 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  3. Ambrosio, L., Pratelli, A.: Existence and stability results in the L1 theory of optimal transportation. In: Optimal Transportation and Applications (Martina Franca, 2001). Lecture Notes in Math., vol. 1813, pp. 123–160. Springer, Berlin (2003)

  4. Bianchini S.: On the Euler–Lagrange equation for a variational problem. Discrete Contin. Dyn. Syst. 17(3), 449–480 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bianchini S., Caravenna L.: On the extremality, uniqueness and optimality of transference plans. Bull. Inst. Math. Acad. Sin. (N.S.) 4(4), 353–454 (2009)

    MathSciNet  MATH  Google Scholar 

  6. Bianchini, S., Cavalletti, F.: Monge Problem in Metric Spaces. Preprint

  7. Bianchini, S., Gloyer, M.: On the Euler Lagrange equation for a variational problem: the general case II. Math. Z. (to appear)

  8. Caffarelli, L., Feldman, M., McCann, R.: Constructing optimal mass for Monge’s transport problem as a limit of strictly convex costs. J. Am. Math. Soc (15), 1–26 (2002)

  9. Champion, T., De Pascale, L.: The Monge problem for strictly convex norms in \({\mathbb {R}^d}\). J. Eur. Math. Soc. (to appear)

  10. Champion, T., De Pascale, L.: The Monge problem in \({\mathbb {R}^d}\). Preprint (2009)

  11. Evans, L.C., Gangbo, W.: Differential equations methods for the Monge–Kantorovich mass transfer problem. Curr. Dev. Math. 65–126 (1997)

  12. Kantorovich L.V.: On the transfer of masses. Docl. Akad. Nauk. SSSR 37, 227–229 (1942)

    Google Scholar 

  13. Kantorovich L.V.: On a problem of Monge. Uskpekhi Mat. Nauk. 3, 225–226 (1948)

    Google Scholar 

  14. Larman D.G.: A compact set of disjoint line segments in \({\mathbb {R}^{3}}\) whose end set has positive measure. Mathematika 18, 112–125 (1971)

    Article  MathSciNet  MATH  Google Scholar 

  15. Monge, G.: Mémoire sur la Theorie des Déblais et des Remblais. Histoire de l’Acad. de Sciences de Paris, pp. 666–704 (1781)

  16. Sudakov, V.N.: Geometric problems in the theory of infinite-dimensional probability distributions. In: Proceedings of Steklov Inst. Math., 2, 1–178, 1979. Number in Russian series statements: t. 141 (1976)

  17. Trudinger, N.S., Wang, X.J.: On the Monge mass transfer problem. Calc. Var. PDE (13), 19–31 (2001)

  18. Villani, C.: Optimal Transport: Old and New, Grundlehren der mathematischen Wissenschaften, vol. 338. Springer, Heidelberg (2009)

Download references

Author information

Authors and Affiliations

  1. SISSA, via Beirut 4, 34014, Trieste, Italy

    Laura Caravenna

Authors
  1. Laura Caravenna
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Laura Caravenna.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Caravenna, L. A proof of Sudakov theorem with strictly convex norms. Math. Z. 268, 371–407 (2011). https://doi.org/10.1007/s00209-010-0677-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00209-010-0677-6

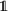Keywords

Search

Navigation