Summary
This paper deals with proper holomorphic self-maps of smoothly bounded pseudoconvex domains in  . We study the dynamical properties of their extension to the boundary and show that their non-wandering sets are always contained in the weakly pseudoconvex part of the boundary. In the case of complete circular domains, we combine this fact with an entropy/degree argument to show that the maps are automorphisms. Some of our results remain true in
. We study the dynamical properties of their extension to the boundary and show that their non-wandering sets are always contained in the weakly pseudoconvex part of the boundary. In the case of complete circular domains, we combine this fact with an entropy/degree argument to show that the maps are automorphisms. Some of our results remain true in 
Similar content being viewed by others
References
Abate, M.: Iteration theory of holomorphic maps on taut manifolds. Research and Lecture Notes in Mathematics. Complex Analysis and Geometry, Mediterranean Press, Rende, 1989
Alexander, H.: Proper holomorphic mappings in C n. Indiana Univ. Math. J. 26(1), 137–146 (1977)
Bedford, E., Bell, S.: Proper self-maps of weakly pseudoconvex domains. Math. Ann. 261(1), 47–49 (1982)
Bell, S.: Local boundary behavior of proper holomorphic mappings. In: Complex analysis of several variables (Madison, Wis., 1982) Proc. Sympos. Pure Math. vol. 41. Amer. Math. Soc., Providence, RI, 1984, pp 1–7
ADFASDFASDF
Berger, M.: Géométrie. 5. CEDIC, Paris, 1977. La sphère pour elle-mOme, géométrie hyperbolique, l'espace des sphères
Berhanu, S., Mendoza, G.A.: Orbits and global unique continuation for systems of vector fields. J. Geom. Anal. 7(2), 173–194 (1997)
Berteloot, F.: Holomorphic vector fields and proper holomorphic self-maps of Reinhardt domains. Ark. Mat. 36(2), 241–254 (1998)
Berteloot, F.,Pinchuk, S.: Proper holomorphic mappings between bounded complete Reinhardt domains in C 2. Math. Z., 219(3), 343–356 (1995)
Boas, H., Straube, E.: Sobolev estimates for the
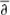 -Neumann operator on domains in C
n admitting a defining function that is plurisubharmonic on the boundary. Math. Z., 206(1), 81–88 (1991)
-Neumann operator on domains in C
n admitting a defining function that is plurisubharmonic on the boundary. Math. Z., 206(1), 81–88 (1991)Chabat, B.: Introduction à l'analyse complexe. Tome 2, Traduit du Russe: Mathématiques. ``Mir'', Moscow, 1990
Coupet, B., Pan, Y., Sukhov, A.: Proper holomorphic self-maps of quasi-circular domains in C 2. Nagoya Math. J. 164, 1–16 (2001)
Diederich, K., Fornæss, J.E.: Proper holomorphic images of strictly pseudoconvex domains. Math. Ann. 259(2), 279–286 (1982)
Dupont, C.: Exemples de Lattès et domaines faiblement sphériques de
 Manuscripta Math. 111(3), 357–378 (2003)
Manuscripta Math. 111(3), 357–378 (2003)Fornæss, J.E., Sibony, N.: Construction of P.S.H. functions on weakly pseudoconvex domains. Duke Math. J. 58(3), 633–655 (1989)
Forstnerič, F.: Proper holomorphic mappings: a survey. Several complex variables (Stockholm, 1987/1988), Math. Notes, vol. 38. Princeton Univ. Press Princeton, NJ, 1993, pp 297–363
Gromov, M.: On the entropy of holomorphic maps. Enseign. Math. (2), 49(3–4), 217–235 (2003)
Henkin, G., Novikov, R.: Proper mappings of classical domains, Vol. 1043. Springer, Berlin, 1984, pp 625–627
Katok, A., Hasselblatt, B.: Introduction to the modern theory of dynamical systems, Vol. 54 of Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 1995
Misiurewicz, M., Przytycki, F.: Topological entropy and degree of smooth mappings. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 25(6), 573–574 (1977)
Nagel, A., Stein, E.M., Wainger, S,: Balls and metrics defined by vector fields. I. Basic properties. Acta Math. 155(1–2), 103–147 (1985)
Pinchuk, S.: The scaling method and holomorphic mappings. In: Several complex variables and complex geometry, Part 1 (Santa Cruz, CA, 1989), Vol. 52. Proc. Sympos. Pure Math., Amer. Math. Soc., Providence, RI, 1991, pp 151–161
Pinchuk, S.I.: Proper holomorphic maps of strictly pseudoconvex domains. Sibirsk. Mat. Ž. 15, 909–917, 959 (1974)
Pinčuk, S.I.: Proper holomorphic mappings of strictly pseudoconvex domains, Petits diviseurs en dimension 1. Dokl. Akad. Nauk SSSR 241(1), 30–33 (1978)
Rudin, W.: Function theory in the unit ball of C n, Vol. 241 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Science]. Springer-Verlag, New York, 1980
Rudin, W.: New constructions of functions holomorphic in the unit ball of C n, Vol. 63 of CBMS Regional Conference Series in Mathematics. Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1986
Sibony, N.: Une classe de domaines pseudoconvexes. Duke Math. J. 55(2), 299–319 (1987)
Tsai, I.H.: Rigidity of proper holomorphic maps between symmetric domains. J. Differential Geom. 37(1), 123–160 (1993)
Tumanov, A.E., Khenkin, G.M.: Local characterization of analytic automorphisms of classical domains. Dokl. Akad. Nauk SSSR 267(4), 796–799 (1982)
Yoccoz, J.-C.: Théorème de Siegel, nombres de Bruno et polynômes quadratiques. Astérisque, 231, 3–88 (1995)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Opshtein, E. Dynamique des applications holomorphes propres de domaines réguliers et problème de l'injectivité. Math. Ann. 335, 1–30 (2006). https://doi.org/10.1007/s00208-005-0689-4
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-005-0689-4



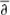 -Neumann operator on domains in C
n admitting a defining function that is plurisubharmonic on the boundary. Math. Z., 206(1), 81–88 (1991)
-Neumann operator on domains in C
n admitting a defining function that is plurisubharmonic on the boundary. Math. Z., 206(1), 81–88 (1991)