Skip to main content
SpringerLink
Log in

Actuation of Thin Nematic Elastomer Sheets with Controlled Heterogeneity

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

Abstract

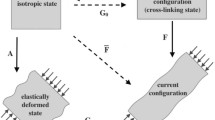
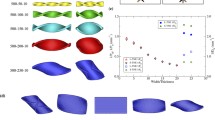
Nematic elastomers and glasses deform spontaneously when subjected to temperature changes. This property can be exploited in the design of heterogeneously patterned thin sheets that deform into a non-trivial shape when heated or cooled. In this paper, we start from a variational formulation for the entropic elastic energy of liquid crystal elastomers and we derive an effective two-dimensional metric constraint, which links the deformation and the heterogeneous director field. Our main results show that satisfying the metric constraint is both necessary and sufficient for the deformation to be an approximate minimizer of the energy. We include several examples which show that the class of deformations satisfying the metric constraint is quite rich.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aharoni H., Sharon E., Kupferman R.: Geometry of thin nematic elastomer sheets. Phys. Rev. Lett. 113(25), 257801 (2014)

    Article  ADS  Google Scholar 

  2. Ball, J.M., James, R.D.: Fine phase mixtures as minimizers of energy. Analysis and Continuum Mechanics, pp. 647–686. Springer, 1989

  3. Barchiesi M., DeSimone A.: Frank energy for nematic elastomers: a nonlinear model. ESAIM Control Optim. Calc. Var. 21(2), 372–377 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  4. Barchiesi, M., Henao, D., Mora-Corral, C.: Local invertibility in Sobolev spaces with applications to nematic elastomers and magnetoelasticity (2015)

  5. Belgacem H.B.: Une méthode de \({\gamma}\)-convergence pour un modele de membrane non linéaire. Comptes Rendus de l’Académie des Sciences-Series I-Mathematics 324(7), 845–849 (1997)

    Article  ADS  MATH  Google Scholar 

  6. Bella P., Kohn R.V.: Metric-induced wrinkling of a thin elastic sheet. J. Nonlinear Sci. 24(6), 1147–1176 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. Bella P., Kohn R.V.: Wrinkles as the result of compressive stresses in an annular thin film. Commun. Pure Appl. Math. 67(5), 693–747 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bhattacharya, K.: Microstructure of martensite: why it forms and how it gives rise to the shape-memory effect, Vol. 2. Oxford University Press, Oxford (2003)

  9. Bhattacharya K., James R.D.: A theory of thin films of martensitic materials with applications to microactuators. J. Mech. Phys. Solids 47(3), 531–576 (1999)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Bhattacharya, K., Lewicka, M., Schäffner, M.: Plates with incompatible prestrain. Arch. Ratio. Mech. Anal., 1–39, 2015

  11. Biggins J., Warner M., Bhattacharya K.: Supersoft elasticity in polydomain nematic elastomers. Phys. Rev. Lett. 103(3), 037802 (2009)

    Article  ADS  Google Scholar 

  12. Biggins J., Warner M., Bhattacharya K.: Elasticity of polydomain liquid crystal elastomers. J. Mech. Phys. Solids 60(4), 573–590 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Bladon P., Terentjev E., Warner M.: Transitions and instabilities in liquid crystal elastomers. Phys. Rev. E 47(6), R3838 (1993)

    Article  ADS  Google Scholar 

  14. Blume J.A.: Compatibility conditions for a left cauchy-green strain field. J. Elast. 21(3), 271–308 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  15. Cesana P., Plucinsky P., Bhattacharya K.: Effective behavior of nematic elastomer membranes. Arch. Ration. Mech. Anal. 218(2), 863–905 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  16. Conti S., DeSimone A., Dolzmann G.: Semisoft elasticity and director reorientation in stretched sheets of nematic elastomers. Phys. Rev. E 66(6), 061710 (2002)

    Article  ADS  Google Scholar 

  17. Conti S., DeSimone A., Dolzmann G.: Soft elastic response of stretched sheets of nematic elastomers: a numerical study. J. Mech. Phys. Solids 50(7), 1431–1451 (2002)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. Conti, S., Dolzmann, G.: Derivation of elastic theories for thin sheets and the constraint of incompressibility. Analysis, Modeling and Simulation of Multiscale Problems, pp. 225–247. Springer, 2006

  19. Conti S., Dolzmann G.: \({\gamma}\)-convergence for incompressible elastic plates. Calc. Var. Partial Differ. Equ. 34, 531–551 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. Conti S., Maggi F.: Confining thin elastic sheets and folding paper. Arch. Rational Mech. Anal. 187, 1–48 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. Dacorogna B.: Direct Methods in the Calculus of Variations, Vol. 78. Springer, Berlin (2007)

    Google Scholar 

  22. de Gennes, P.G., Prost, J.: The Physics of Liquid Crystals, No. 83. Oxford University Press, Oxford, 1995

  23. de Haan, L.T., Sánchez-Somolinos, C., Bastiaansen, C.M., Schenning, A.P., Broer, D.J.: Engineering of complex order and the macroscopic deformation of liquid crystal polymer networks. Angew. Chem. Int. Ed. 51(50), 12469–12472, 2012

  24. DeSimone A.: Energy minimizers for large ferromagnetic bodies. Arch. Rational Mech. Anal. 125(2), 99–143 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  25. DeSimone A., Dolzmann G.: Macroscopic response of nematic elastomers via relaxation of a class of so (3)-invariant energies. Arch. Rational Mech. Anal., 161(3), 181–204 (2002)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. Efrati E., Sharon E., Kupferman R.: The metric description of elasticity in residually stressed soft materials. Soft Matter 9(34), 8187–8197 (2013)

    Article  ADS  Google Scholar 

  27. Friesecke G., James R.D., Müller S.: A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Commun. Pure Appl. Math. 55, 1461–1506 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  28. Friesecke G., James R.D., Müller S.: A hierarchy of plate models derived from nonlinear elasticity by gamma-convergence. Arch. Rational Mech. Anal. 180(2), 183–236 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Fuchi K., Ware T.H., Buskohl P.R., Reich G.W., Vaia R.A., White T.J., Joo J.J.: Topology optimization for the design of folding liquid crystal elastomer actuators. Soft matter 11(37), 7288–7295 (2015)

    Article  ADS  Google Scholar 

  30. Gimenez-Pinto, V., Ye, F., Mbanga, B., Selinger, J.V., Selinger, R.L.: Modeling out-of-plane actuation in thin-film nematic polymer networks: from chiral ribbons to auto-origami boxes via twist and topology. Sci. Rep. 7, 2017

  31. Hornung P.: Approximation of flat W 2, 2 isometric immersions by smooth ones. Arch. Rational Mech. Anal. 199(3), 1015–1067 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. Kundler I., Finkelmann H.: Strain-induced director reorientation in nematic liquid single crystal elastomers. Macromol. Rapid Commun. 16(9), 679–686 (1995)

    Article  Google Scholar 

  33. Lewicka M., Mahadevan L., Pakzad M.R.: The föppl-von kármán equations for plates with incompatible strains. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 467, 402–426 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. Lewicka M., Pakzad M.R.: Scaling laws for non-euclidean plates and the W 2, 2 isometric immersions of riemannian metrics. ESAIM Control Optim. Calc. Var. 17(04), 1158–1173 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  35. Modes C., Bhattacharya K., Warner M.: Gaussian curvature from flat elastica sheets. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 467, 1121–1140 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  36. Modes C.D., Warner M.: Blueprinting nematic glass: Systematically constructing and combining active points of curvature for emergent morphology. Phys. Rev. E 84(2), 021711 (2011)

    Article  ADS  Google Scholar 

  37. Modes C.D., Warner M.: Shape-programmable materials. Phys. Today 69(1), 32–38 (2016)

    Article  ADS  Google Scholar 

  38. Modica L.: The gradient theory of phase transitions and the minimal interface criterion. Arch. Rational Mech. Anal. 98(2), 123–142 (1987)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. Modica L., Mortola S.: Un esempio di \({\gamma}\)-convergenza. Boll. Un. Mat. Ital. B (5) 14(1), 285–299 (1977)

    MathSciNet  MATH  Google Scholar 

  40. Mostajeran C.: Curvature generation in nematic surfaces. Phys. Rev. E, 91(6), 062405 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  41. Mostajeran, C., Warner, M., Ware, T.H., White, T.J.: Encoding gaussian curvature in glassy and elastomeric liquid crystal solids. Proc. R. Soc. A 472, 20160112, 2016

  42. Nguyen, T.-S., Selinger, J.V.: Theory of liquid crystal elastomers: From polymer physics to differential geometry. 2016. arXiv preprint arXiv:1612.06486

  43. Pakzad M.R. et al.: On the Sobolev space of isometric immersions. J. Differ. Geom. 66(1), 47–69 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  44. Plucinsky, P.: The Deformations of Thin Nematic Elastomer Sheets. Ph.D. thesis, California Institute of Technology, 2017

  45. Plucinsky P., Lemm M., Bhattacharya K.: Programming complex shapes in thin nematic elastomer and glass sheets. Phys. Rev. E 94, 010701 (2016)

    Article  ADS  Google Scholar 

  46. Tajbakhsh A., Terentjev E.: Spontaneous thermal expansion of nematic elastomers. Eur. Phys. J. E 6(2), 181–188 (2001)

    Article  Google Scholar 

  47. Trabelsi K.: Modeling of a membrane for nonlinearly elastic incompressible materials via gamma-convergence. Anal. Appl. 4(01), 31–60 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  48. Verwey G., Warner M.: Compositional fluctuations and semisoftness in nematic elastomers. Macromolecules 30(14), 4189–4195 (1997)

    Article  ADS  Google Scholar 

  49. Verwey G., Warner M., Terentjev E.: Elastic instability and stripe domains in liquid crystalline elastomers. Journal de Physique II 6(9), 1273–1290 (1996)

    Article  ADS  Google Scholar 

  50. Ware T.H., McConney M.E., Wie J.J., Tondiglia V.P., White T.J.: Voxelated liquid crystal elastomers. Science 347(6225), 982–984 (2015)

    Article  ADS  Google Scholar 

  51. Warner M., Modes C., Corbett D.: Curvature in nematic elastica responding to light and heat. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 466, 2975–2989 (2010)

    Article  ADS  MATH  Google Scholar 

  52. Warner, M., Terentjev, E.M.: Liquid Crystal Elastomers, Vol. 120. OUP Oxford, Oxford, 2003

Download references

Author information

Authors and Affiliations

  1. California Institute of Technology, Pasadena, CA, 91125, USA

    Paul Plucinsky, Marius Lemm & Kaushik Bhattacharya

Authors
  1. Paul Plucinsky
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marius Lemm
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kaushik Bhattacharya
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kaushik Bhattacharya.

Additional information

Communicated by R. James

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Plucinsky, P., Lemm, M. & Bhattacharya, K. Actuation of Thin Nematic Elastomer Sheets with Controlled Heterogeneity. Arch Rational Mech Anal 227, 149–214 (2018). https://doi.org/10.1007/s00205-017-1167-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-017-1167-3

Search

Navigation