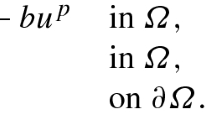Abstract
We study global bifurcation curves and the exact multiplicity of positive solutions for the two-point boundary value problem arising in combustion theory:
where \({\lambda > 0}\) is the Frank–Kamenetskii parameter and a > 0 is the activation energy parameter. We prove that there exists a critical bifurcation value a 0 \({\approx 4.069}\) such that, on the \({(\lambda,||u||_{\infty })}\)-plane, the bifurcation curve is S-shaped for \({a > a_{0}}\) and is monotone increasing for \({0 < a \leqq a_{0}}\). That is, we prove the long-standing conjecture for the one-dimensional perturbed Gelfand problem. We also study, in the \({(a,\lambda, \left \Vert u\right\Vert _{\infty})}\)-space, the shape and structure of the bifurcation surface.
Similar content being viewed by others
References
Bebernes J., Eberly D.: Mathematical problems from combustioneory. Springer-Verlag, New York (1989)
Boddington T., Gray P., Robinson C.: Thermal explosion and the disappearance of criticality at small activation energies: exact results for the slab. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 368, 441–461 (1979)
Brown K.J., Ibrahim M.M.A., Shivaji R.: S-shaped bifurcation curves. Nonlinear Anal. 5, 475–486 (1981)
Crandall M.G., Rabinowitz P.H.: Bifurcation, perturbation of simple eigenvalues and linearized stability. Arch. Rational Mech. Anal. 52, 161–180 (1973)
Cohn P.M.: Basic algebra: groups, rings and fields. Springer-Verlag, London (2003)
Du Y.: Exact multiplicity and S-shaped bifurcation curve for some semilinear elliptic problems from combustion theory. SIAM J. Math. Anal. 32, 707–733 (2000)
Du Y., Lou Y.: Proof of a conjecture for the perturbed Gelfand equation from combustion theory. J. Differ. Equ. 173, 213–230 (2001)
Forde J., Nelson P.: Applications of Sturm sequences to bifurcation analysis of delay differential equation models. J. Math. Anal. Appl. 300, 273–284 (2004)
Gelfand I.M.: Some problems in the theory of quasilinear equations. Am. Math. Soc. Transl. (2) 29, 295–381 (1963)
Hastings S.P., McLeod J.B.: The number of solutions to an equation from catalysis. Proc. R. Soc. Edinb. Sect. A 101, 15–30 (1985)
Hastings S.P., McLeod J.B.: Classical methods in ordinary differential equations: With applications to boundary value problems. Graduate Studies in Mathematics, vol. 129. American Mathematical Society, Providence, 2012
Huang S.-Y., Wang S.-H.: On S-shaped bifurcation curves for a two-point boundary value problem arising in a theory of thermal explosion. Discrete Contin. Dyn. Syst. 35, 4839–4858 (2015)
Huang, S.-Y., Wang, S.-H.: Tasks in computations in some proofs (2015). http://mx.nthu.edu.tw/~sy-huang/Gelfand/works.htm
Hung K.-C., Wang S.-H.: A theorem on S-shaped bifurcation curve for a positone problem with convex-concave nonlinearity and its applications to the perturbed Gelfand problem. J. Differ. Equ. 251, 223–237 (2011)
Hung K.-C., Wang S.-H.: Global bifurcation and exact multiplicity of positive solutions for a positone problem with cubic nonlinearity and their applications. Trans. Am. Math. Soc. 365, 1933–1956 (2013)
Jacobsen J., Schmitt K.: The Liouville-Bratu-Gelfand problem for radial operators. J. Differ. Equ. 184, 283–298 (2002)
Kapila A.K., Matkowsky B.J.: Reactive-diffuse systems with Arrhenius kinetics: multiple solutions, ignition and extinction. SIAM J. Appl. Math. 36, 373–389 (1979)
Korman P., Li Y.: On the exactness of an S-shaped bifurcation curve. Proc. Am. Math. Soc. 127, 1011–1020 (1999)
Korman P., Li Y., Ouyang T.: Computing the location and direction of bifurcation. Math. Res. Lett. 12, 933–944 (2005)
Laetsch T.: The number of solutions of a nonlinear two point boundary value problem. Indiana Univ. Math. J. 20, 1–13 (1970)
Liouville J.: Sur l’équation aux différences partielles \({\frac{d^{2} \log \lambda }{dudv} \pm \lambda 2a^{2}=0}\). J. Math. Pures Appl. 18, 71–72 (1853)
Mimura M., Sakamoto K.: Multi-dimensional transition layers for an exothermic reaction-diffusion system in long cylindrical domains. J. Math. Sci. Univ. Tokyo 3, 109–179 (1996)
Prestel A., Delzell C.N.: Positive polynomials: from Hilbert’s 17th problem to real algebra. Springer-Verlag, Berlin (2001)
Shi J.: Persistence and bifurcation of degenerate solutions. J. Funct. Anal. 169, 494–531 (1999)
Shi J.: Multi-parameter bifurcation and applications. Topological methods, variational methods and their applications (Taiyuan, 2002), pp. 211–221, World Sci. Publ., River Edge, 2003
Shivaji R.: Remarks on an S-shaped bifurcation curve. J. Math. Anal. Appl. 111, 374–387 (1985)
Smoller J., Wasserman A.: Global bifurcation of steady-state solutions. J. Differ. Equ. 39, 269–290 (1981)
Wang S.-H.: On S-shaped bifurcation curves. Nonlinear Anal. TMA 22, 1475–1485 (1994)
Zeldovich Ya.B., Barenblatt G.I., Librovich, V.B., Makhviladze G.M.: The mathematical theory of combustion and explosions. Consultants Bureau [Plenum], New York 1985
Zhang M., Deng J.: Number of zeros of interval polynomials. J. Comput. Appl. Math. 237, 102–110 (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Rabinowitz
This work is partially supported by the National Science Council of the Republic of China under Grant No. NSC 101-2115-M-007-001-MY2.
Rights and permissions
About this article
Cite this article
Huang, SY., Wang, SH. Proof of a Conjecture for the One-Dimensional Perturbed Gelfand Problem from Combustion Theory. Arch Rational Mech Anal 222, 769–825 (2016). https://doi.org/10.1007/s00205-016-1011-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-016-1011-1