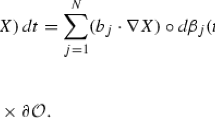Abstract
In this work, we introduce a new method to prove the existence and uniqueness of a variational solution to the stochastic nonlinear diffusion equation \({{\rm d}X(t) = {\rm div} \left[\frac{\nabla X(t)}{|\nabla X(t)|}\right]{\rm d}t + X(t){\rm d}W(t) {\rm in} (0, \infty) \times \mathcal{O},}\) where \({\mathcal{O}}\) is a bounded and open domain in \({\mathbb{R}^N, N \geqq 1}\) and W(t) is a Wiener process of the form \({W(t) = \sum^{\infty}_{k = 1}\mu_{k}e_{k}\beta_{k}(t), e_{k} \in C^{2}(\overline{\mathcal{O}}) \cap H^{1}_{0}(\mathcal{O}),}\) and \({\beta_{k}, k \in \mathbb{N}}\) are independent Brownian motions. This is a stochastic diffusion equation with a highly singular diffusivity term. One main result established here is that for all initial conditions in \({L^2(\mathcal{O})}\), it is well posed in a class of continuous solutions to the corresponding stochastic variational inequality. Thus, one obtains a stochastic version of the (minimal) total variation flow. The new approach developed here also allows us to prove the finite time extinction of solutions in dimensions \({1\leqq N \leqq3}\), which is another main result of this work.
Similar content being viewed by others
References
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems, Oxford Universityt Press, New York, 2000
Andreu F., Caselles V., Dí az J., Mazón J.: Some qualitative properties for the total variation flow. J. Funct. Anal. 188, 516–547 (2002)
Andreu-Vaillo, F., Caselles, V., Mazón, J.M.: Parabolic Quasilinear Equations Minimizing Linear Growth Functionals. Progress in Mathematics 223, Birkhäuser, Basel, 2004
Attouch, H., Buttazzo, G., Gerard, M.: Variational Analysis in Sobolev Spaces and BV Spaces; Applications to PDES and Optimization. SIAM Series on Optimization, Philadelphia, 2006
Barbu, V.: Nonlinear Differential Equations of Monotone Type in Banach Spaces. Springer, New York, 2010
Barbu T., Barbu V., Biga V., Coca D.: A PDE variational approach to image denoising and restoration.. Nonlinear Analysis Real World Applications 10, 1351–1361 (2009)
Barbu V., Da Prato G., Röckner M.: Existence and uniqueness of nonnegative solutions to the stochastic porous media equation. Indiana Univ. Math. J. 57, 187–212 (2008)
Barbu, V., Da Prato, G., Röckner M.: Stochastic nonlinear diffusion equations with singular diffusivity. SIAM J. Math. Anal. 41, 3, 1106–1120 (2009)
Barbu V., Da Prato G., Röckner M.: Stochastic porous media equations and self-organized criticality. Comm. Math. Phys. 285, 901–923 (2009)
Barbu V., Da Prato G., Röckner M.: Finite time extinction of solutions to fast diffusion equation driven by linear multiplicative noise. J. Math. Anal. Appl. 389, 147–164 (2012)
Barbu, V., Da Prato, G., Röckner M.: Addendum to “Stochastic nonlinear diffusion equations with singular diffusivity. CRC 701-Preprint 2011, Universität Bielefeld
Barbu V., Röckner M.: On a random scaled porous media equation. J. Differ. Equ. 251, 2494–2514 (2011)
Barbu V., Röckner M.: Stochastic porous media equations and self-organized criticality: convergence to the critical state in all dimensions. Commun. Math. Phys. 311, 539–555 (2012)
Brezis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, Berlin, 2010
Brezis, H.: Opérateurs maximaux monotones et semigroupes de contractions dans les espaces de Hilbert. North-Holland, Amsterdam, 1973
Brezis, H.: Personal communication and detailed paper in preparation.
Brezis H., Stampacchia G.: Sur la régularité de la solution d’inéquations elliptiques.. Bulletin de la SMF 96, 153–180 (1968)
Chamballe A., Lions P.L.: Image recovery via total variation minimization. Numer. Math. 76, 17–31 (1997)
Chan, T., Esedogly, S., Park, F., Yip, A.: Total variation image restoration. Overview and recent developments. In Handbook of Mathematical Models in Computer Vision, Springer, New York, 2006
Ciotir I., Tolle J.T.: Convergence of invariant measures for singular stochastic diffusion equations. Stoch. Process. Appl. 122, 1998–2017 (2012)
Da Prato, G., Zabczyk, J.: Stochastic Equations in Infinite Dimensions. Cambridge University Press, Cambridge, 1992
Gess, B., Tölle, J.M.: Multivalued singular stochastic evolution inclusion. http://arxiv.org/ads/112.5672
Giga Y., Kobayashi R.: On constrained equations with singular diffusivity. Methods Appl. Anal. 10(2), 253–278 (2003)
Giga M.H., Giga Y.: Generalized motion by non local curvature in the plane. Arch. Rat. Mech. Anal. 159, 295–333 (2001)
Giga Y., Kohn R.V.: Scale invariant extinction time estimates for some singular diffusion equations. Discret. Contin. Dynam. Syst. Ser. A , 30, 509–535 (2011)
Kobayashi R., Giga Y.: Equations with singular diffusivity. J. Stat. Phys. 95, 1187–1220 (1999)
Krylov, N.V., Rozovskii, B.L.: Stochastic evolution equations. Curr. Probl. Math. 14 (Russian), Acad. Nauk SSSR, 71–147 (1979)
Krylov, N.V.: Itô’s formula for the L p -norm of a stochastic \({W^1_p}\) -valued process. Probab. Theory Relat. Fields 147, 583–605 (2010)
Pardoux, E.: Equations aux dérivées partielles stochastiques non linéaires monotones, étude de solutions fortes de type Itô. Thèse Université Paris Sud, Orsay, 1975
Prevot, C., Röckner, M.: A Concise Course on Stochastic Partial Differential Equations. Lecture Notes in Math., 1905, Berlin, 2007
Rudin L.I., Osher S., Fatemi E.: Nonlinear total variational based noise removal algorithms.. Physica D 60, 259–268 (1992)
Taira, K.: Analytic Semigroups and Semilinear Initial Boundary Value Problems, Cambridge University Press, Cambridge, 1995
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Dafermos
Rights and permissions
About this article
Cite this article
Barbu, V., Röckner, M. Stochastic Variational Inequalities and Applications to the Total Variation Flow Perturbed by Linear Multiplicative Noise. Arch Rational Mech Anal 209, 797–834 (2013). https://doi.org/10.1007/s00205-013-0632-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-013-0632-x