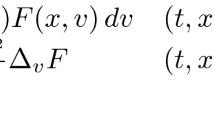Skip to main content
SpringerLink
Log in

N-particles Approximation of the Vlasov Equations with Singular Potential

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

Abstract

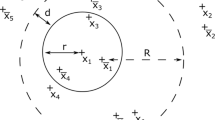
We prove the convergence in any time interval of a point-particle approximation of the Vlasov equation by particles initially equally separated for a force in 1/|x|α, with \(\alpha \leqq 1\). We introduce discrete versions of the L ∞ norm and time averages of the force-field. The core of the proof is to show that these quantities are bounded and that consequently the minimal distance between particles in the phase space is bounded from below.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Batt, J.: N-Particle approximation to the nonlinear Vlasov–Poisson system. Preprint

  2. Bouchut F. (1995). Smoothing effect for the non-linear Vlasov–Poisson–Fokker–Planck system. J. Differential Equations 122:225–238

    Article  MathSciNet  MATH  Google Scholar 

  3. Batt J., Rein G. (1991). Global classical solutions of the periodic Vlasov–Poisson system in three dimensions. C.R. Math. Acad. Sci. Paris 313:411–416

    MathSciNet  MATH  Google Scholar 

  4. Braun W., Hepp K. (1977). The Vlasov dynamics and its fluctuations in the 1/N limit of interacting classical particles. Comm. Math. Phys. 56:101–113

    Article  ADS  MathSciNet  Google Scholar 

  5. Cercignani C., Illner R., Pulvirenti M. (1994). The Mathematical Theory of Dilute Gases. Applied Mathematical Sciences, 106, Springer-Verlag, New York

    MATH  Google Scholar 

  6. Dobrušin R.L. (1979). Vlasov equations. Funktsional. Anal. i Prilozhen. 13:48–58

    Article  MathSciNet  Google Scholar 

  7. Gasser I., Jabin P.E., Perthame B. (2000). Regularity and propagation of moments in some nonlinear Vlasov systems. Proc. Roy. Soc. Edinburgh Sect. A 130:1259–1273

    MathSciNet  MATH  Google Scholar 

  8. Glassey R.T. (1996). The Cauchy Problem in Kinetic Theory. SIAM, Philadelphia PA

    MATH  Google Scholar 

  9. Goodman J., Hou T.Y., Lowengrub J. (1990). Convergence of the point vortex method for the 2-D Euler equations. Comm. Pure Appl. Math. 43:415–430

    MathSciNet  MATH  Google Scholar 

  10. Horst E. (1981). On the classical solutions of the initial value problem for the unmodified non-linear Vlasov equation I. Math. Methods Appl. Sci. 3:229–248

    MathSciNet  MATH  ADS  Google Scholar 

  11. Horst E. (1982). On the classical solutions of the initial value problem for the unmodified non-linear Vlasov equation II. Math. Methods Appl. Sci. 4:19–32

    ADS  MathSciNet  MATH  Google Scholar 

  12. Illner R., Pulvirenti M. (1989). Global validity of the Boltzmann equation for two and three-dimensional rare gas in vacuum. Comm. Math. Phys. 121:143–146

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Jabin P.E., Otto F. (2004). Identification of the dilute regime in particle sedimentation. Comm. Math. Phys. 250:415–432

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Jabin, P.E., Perthame, B.: Notes on mathematical problems on the dynamics of particles interacting through a fluid. Modelling in Applied Sciences (Ed. Bellomo, P., Pulvirenti, M.), pp. 111–147, Modelling and Simulation in Science, Engineering and Technology, Birkhauser, Boston, 2000

  15. Lions P.L., Perthame B. (1991). Propagation of moments and regularity for the 3-dimensional Vlasov–Poisson System. Invent. Math. 105:415–430

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Neunzert, H., Wick, J.: Theoretische und numerische Ergebnisse zur nichtlinearen Vlasov–Gleichung. Numerische Lösung nichtlinearer partieller Differential- und Integrodifferentialgleichungen (Tagung, Math. Forschungsinst., Oberwolfach, 1971), pp. 159–185. Lecture Notes in Mathematics, Vol. 267, Springer, Berlin, 1972

  17. Perthame B. (1996). Time decay, propagation of low moments and dispersive effects for kinetic equations. Comm. Partial Differential Equations 21:659–686

    MathSciNet  MATH  Google Scholar 

  18. Pfaffelmoser K. (1992). Global classical solutions of the Vlasov–Poisson system in three dimensions for general initial data. J. Differential Equations 95:281–303

    Article  MathSciNet  MATH  Google Scholar 

  19. Pulvirenti M., Simeoni C. (2000). L ∞-estimates for the Vlasov–Poisson–Fokker–Planck Equation. Math. Methods Appl. Sci. 23:923–935

    Article  MathSciNet  MATH  ADS  Google Scholar 

  20. Schaeffer J. (1991). Global existence of smooth solutions to the Vlasov–Poisoon system in three dimensions. Comm. Partial Differential Equations 16:1313–1335

    MathSciNet  MATH  Google Scholar 

  21. Schochet S. (1995). The weak vorticity formulation of the 2-D Euler equations and concentration-cancellation. Comm. Partial Differential Equations 20:1077–1104

    MathSciNet  MATH  Google Scholar 

  22. Schochet S. (1996). The point-vortex method for periodic weak solutions of the 2-D Euler equations. Comm. Pure Appl. Math. 49:911–965

    Article  MathSciNet  MATH  Google Scholar 

  23. Spohn, H.: Large Scale Dynamics of Interacting Particles. Springer-Verlag Berlin 1991

  24. Victory H.D. jr., Allen E.J. (1991). The convergence theory of particle-in-cell methods for multidimensional Vlasov–Poisson systems. SIAM J. Numer. Anal. 28:1207–1241

    Article  MathSciNet  MATH  Google Scholar 

  25. Wollman S. (2000). On the approximation of the Vlasov–Poisson system by particles methods. SIAM J. Numer. Anal. 37:1369–1398

    Article  MathSciNet  MATH  Google Scholar 

  26. Wollman S. (1993). Global in time solutions to the three-dimensional Vlasov–Poisson System. J. Math. Anal. Appl. 176:76–91

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire Jacques-Louis Lions, U.M.R. no 7598 du C.N.R.S., Université Pierre et Marie Curie, Boîte courrier 187, 75252, Paris Cedex 05, France

    Maxime Hauray

  2. Laboratoire J.-A. Dieudonn, U.M.R. no 6621 du C.N.R.S., Université de Nice – Sophia Antipolis Parc Valrose, 06108, Nice Cedex 02, France

    Pierre-Emmanuel Jabin

Authors
  1. Maxime Hauray
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pierre-Emmanuel Jabin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maxime Hauray.

Additional information

Communicated by P-L. Lions

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hauray, M., Jabin, PE. N-particles Approximation of the Vlasov Equations with Singular Potential. Arch Rational Mech Anal 183, 489–524 (2007). https://doi.org/10.1007/s00205-006-0021-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-006-0021-9

Keywords

Search

Navigation