Skip to main content
SpringerLink
Log in

Kinetic Limit for Wave Propagation in a Random Medium

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

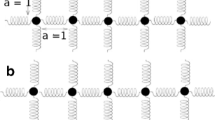
We study crystal dynamics in the harmonic approximation. The atomic masses are weakly disordered, in the sense that their deviation from uniformity is of the order \(\sqrt{\epsilon}\). The dispersion relation is assumed to be a Morse function and to suppress crossed recollisions. We then prove that in the limit \(\epsilon\to 0\), the disorder-averaged Wigner function on the kinetic scale, time and space of order \(\epsilon^{-1}\), is governed by a linear Boltzmann equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bal G., Fannjiang A., Papanicolaou G., Ryzhik L. (1999) Radiative transport in a periodic structure. J. Stat. Phys. 95, 479–494

    Article  MATH  MathSciNet  Google Scholar 

  2. Bal G., Komorowski T., Ryzhik L. (2003) Self-averaging of Wigner transforms in random media. Comm. Math. Phys. 242, 81–135

    MATH  MathSciNet  ADS  Google Scholar 

  3. Chen T. (2005) Localization lengths and Boltzmann limit for the Anderson model at small disorders in dimension 3. J. Stat. Phys. 120, 279–337

    Article  MathSciNet  Google Scholar 

  4. Chen, T.: L r-Convergence of a random Schrödinger to a linear Boltzmann evolution. Preprint (2004) arXiv.org:math-ph/0407037

  5. Eng D., Erdős L. (2005) The linear Boltzmann equation as the low density limit of a random Schrödinger equation. Rev. Math. Phys. 17, 669–743

    Article  MATH  MathSciNet  Google Scholar 

  6. Erdős L. (2002) Linear Boltzmann equation as the long time dynamics of an electron weakly coupled to a phonon field. J. Stat. Phys. 107, 1043–1127

    Article  Google Scholar 

  7. Erdős, L., Salmhofer, M., Yau, H.-T.: Quantum diffusion of random Schrödinger evolution in the scaling limit. Preprint (2005) arXiv.org: math-ph/0502025

  8. Erdős L., Yau H.-T. (2000) Linear Boltzmann equation as the weak coupling limit of a random Schrödinger equation. Comm. Pure Appl. Math. 53, 667–735

    Article  MathSciNet  Google Scholar 

  9. Gelfand I.M., Shilov G.E. (1968) Generalized Functions II. Academic Press, New York

    Google Scholar 

  10. Gérard P., Markowich P.A., Mauser N.J., Paupaud F. (1997) Homogenization limits and Wigner transforms. Comm. Pure Appl. Math. 50, 323–379

    Article  MATH  MathSciNet  Google Scholar 

  11. Hörmander L. (1983) The Analysis of Linear Partial Differential Operators I: Distribution Theory and Fourier Analysis. Springer, Berlin

    Google Scholar 

  12. Klein, A.: Multiscale analysis and localization of random operators. Random Schrödinger Operators: Methods, Results, and Perspectives, Panorama & Synthèse, Société Mathématique de France, to appear. Preprint (2004)http://www.ma.utexas.edu/mp_arc/ c/04/04-1.pdf

  13. Lukkarinen, J.: Asymptotics of resolvent integrals: The suppression of crossings for analytic lattice dispersion relations. In preparation

  14. Macià F. (2004) Wigner measures in the discrete setting: High-frequency analysis of sampling and reconstruction operators. SIAM J. Math. Anal. 36, 347–383

    Article  MATH  MathSciNet  Google Scholar 

  15. Mielke, A.: Macroscopic behavior of microscopic oscillations in harmonic lattices via Wigner–Husimi transforms. Arch. Ration. Mech. Anal. DOI: 10.1007/s00205-005-0405-2

  16. Rudin W., (1974) Functional Analysis. Tata McGraw-Hill, New Delhi

    MATH  Google Scholar 

  17. Ryzhik L., Papanicolaou G., Keller J.B. (1996) Transport equations for elastic and other waves in random media. Wave Motion 24, 327–370

    Article  MATH  MathSciNet  Google Scholar 

  18. Spohn, H.: The phonon Boltzmann equation, properties and link to weakly anharmonic lattice dynamics. Preprint (2005) arXiv.org: math-ph/0505025. To be published in J. Stat. Phys

  19. Teufel, S., Panati, G.: Propagation of Wigner functions for the Schrödinger equation with a perturbed periodic potential. Multiscale Methods in Quantum Mechanics (Eds. Blanchard, Ph., Dell’Antonio, G.), Birkhäuser, Boston, 2004

  20. Wawrzyńczyk A. (1968) On tempered distributions and Bochner-Schwartz theorem on arbitrary locally compact Abelian groups. Colloq. Math. 19, 305–318

    MathSciNet  Google Scholar 

  21. Ziman J.M. (1967) Electrons and Phonons: The Theory of Transport Phenomena in Solids. Oxford University Press, London

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Zentrum Mathematik, Technische Universität München, Boltzmannstr. 3, D-85747, Garching, Germany

    Jani Lukkarinen & Herbert Spohn

Authors
  1. Jani Lukkarinen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Herbert Spohn
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jani Lukkarinen.

Additional information

Communicated by J. Fritz

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lukkarinen, J., Spohn, H. Kinetic Limit for Wave Propagation in a Random Medium. Arch Rational Mech Anal 183, 93–162 (2007). https://doi.org/10.1007/s00205-006-0005-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-006-0005-9

Keywords

Search

Navigation