Abstract.
In this paper, we prove a new existence result for a variational model of crack growth in brittle materials proposed in [19]. We consider the case of n-dimensional nonlinear elasticity, for an arbitrary n≧1, with a quasiconvex bulk energy and with prescribed boundary deformations and applied loads, both depending on time.
Similar content being viewed by others
References
Ambrosio, L.: A compactness theorem for a new class of functions of bounded variation. Boll. Un. Mat. Ital. B (7) 3, 857–881 (1989)
Ambrosio, L.: Existence theory for a new class of variational problems. Arch. Rational Mech. Anal. 111, 291–322 (1990)
Ambrosio, L.: On the lower semicontinuity of quasi-convex functionals in SBV. Nonlinear Anal. 23, 405–425 (1994)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of bounded variation and free discontinuity problems. Oxford University Press, Oxford, 2000
Brezis, H.: Opérateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert. North-Holland, Amsterdam-London; American Elsevier, New York, 1973
Brezis, H.: Convergence in
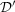 and in L1 under strict convexity. Boundary value problems for partial differential equations and applications, 43–52, RMA Res. Notes Appl. Math., 29, Masson, Paris, 1993
and in L1 under strict convexity. Boundary value problems for partial differential equations and applications, 43–52, RMA Res. Notes Appl. Math., 29, Masson, Paris, 1993Chambolle, A.: A density result in two-dimensional linearized elasticity, and applications. Arch. Rational Mech. Anal. 167, 211–233 (2003)
Dacorogna, B.: Direct methods in the calculus of variations. Springer-Verlag, Berlin, 1989
Dal Maso, G., Francfort, G.A., Toader, R.: Quasi-static crack growth in finite elasticity. Preprint SISSA, Trieste, 2004 (http://www.sissa.it/fa/)
Dal Maso, G., Francfort, G.A., Toader, R.: Quasi-static crack evolution in brittle fracture: the case of bounded solutions. Calculus of Variations. Topics from the mathematical heritage of Ennio De Giorgi. Quaderni di Matematica, Dipartimento di Matematica della Seconda Università di Napoli, 2004, to appear (http://www.sissa.it/fa/)
Dal Maso, G., Giacomini, A., Ponsiglione, M.: Some qualitative properties of solutions to variational models for quasistatic crack growth. In preparation
Dal Maso, G., Toader, R.: A model for the quasi-static growth of brittle fractures: existence and approximation results. Arch. Rational Mech. Anal. 162, 101–135 (2002)
De Giorgi, E., Ambrosio, L.: Un nuovo tipo di funzionale del calcolo delle variazioni. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. (8) 82, 199–210 (1988)
De Giorgi, E., Carriero, M., Leaci, A.: Existence theorem for a minimum problem with free discontinuity set. Arch. Rational Mech. Anal. 108, 195–218 (1989)
Doob, J.L.: Stochastic processes. Wiley, New York, 1953
Federer, H.: Geometric measure theory. Springer-Verlag, Berlin, 1969
Francfort, G.A., Larsen, C.J.: Existence and convergence for quasi-static evolution in brittle fracture. Commun. Pure Appl. Math. 56, 1465–1500 (2003)
Francfort, G.A., Marigo, J.-J.: Stable damage evolution in a brittle continuous medium. European J. Mech. A Solids 12, 149–189 (1993)
Francfort, G.A., Marigo, J.-J.: Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 46, 1319–1342 (1998)
Griffith, A.: The phenomena of rupture and flow in solids. Philos. Trans. Roy. Soc. London Ser. A 221, 163–198 (1920)
Hahn, H.: Über Annäherung an Lebesgue’sche Integrale durch Riemann’sche Summen. Sitzungsber. Math. Phys. Kl. K. Akad. Wiss. Wien 123, 713–743 (1914)
Henstock, R.: A Riemann-type integral of Lebesgue power. Canad. J. Math. 20, 79–87 (1968)
Krasnosel’skii, M.A.: Topological methods in the theory of nonlinear integral equations. Pergamon Press, Oxford, 1964
Kristensen, J.: Lower semicontinuity in spaces of weakly differentiable functions. Math. Ann. 313, 653–710 (1999)
Mainik, A., Mielke, A.: Existence results for energetic models for rate-independent systems. Calc. Var. Partial Differential Equations, 2004, to appear.
Mawhin, J.: Analyse. Fondements, techniques, évolution. Second edition. Accès Sciences. De Boeck Université, Brussels, 1997
Mielke, A., Theil, F.: A mathematical model for rate-independent phase transformations with hysteresis. In: Alber, H.-D., Balean, R., Farwig, R. (eds.), Proceedings of the Workshop on ‘‘Models of continuum mechanics in analysis and engineering’’ (1999), Shaker-Verlag, pp. 117–129
Mielke, A., Theil, F., Levitas, V.: A variational formulation of rate-independent phase transformations using an extremum principle. Arch. Rational Mech. Anal. 162, 137–177 (2002)
Nečas, J.: Les méthodes directes en théorie des équations elliptiques. Academia, Prague, 1967
Saks, S.: Sur les fonctions d’intervalle. Fund. Math. 10, 211–224 (1927)
Visintin, A.: Strong convergence results related to strict convexity. Commun. Partial Differential Equations 9, 439–466 (1984)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Mielke
Rights and permissions
About this article
Cite this article
Maso, G., Francfort, G. & Toader, R. Quasistatic Crack Growth in Nonlinear Elasticity. Arch. Rational Mech. Anal. 176, 165–225 (2005). https://doi.org/10.1007/s00205-004-0351-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-004-0351-4





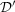 and in L1 under strict convexity. Boundary value problems for partial differential equations and applications, 43–52, RMA Res. Notes Appl. Math., 29, Masson, Paris, 1993
and in L1 under strict convexity. Boundary value problems for partial differential equations and applications, 43–52, RMA Res. Notes Appl. Math., 29, Masson, Paris, 1993